Teoria automatów - szybki przewodnik
Automata - co to jest?
Termin „automata” pochodzi od greckiego słowa „αὐτόματα”, które oznacza „samoczynne działanie”. Automat (w liczbie mnogiej Automata) to abstrakcyjne samobieżne urządzenie obliczeniowe, które automatycznie wykonuje z góry określoną sekwencję operacji.
Automat ze skończoną liczbą stanów nazywany jest a Finite Automaton (FA) lub Finite State Machine (FSM).
Formalna definicja automatu skończonego
Automat można przedstawić jako 5-krotkę (Q, ∑, δ, q 0 , F), gdzie -
Q jest skończonym zbiorem stanów.
∑ jest skończonym zbiorem symboli, zwanym alphabet automatu.
δ jest funkcją przejścia.
q0jest stanem początkowym, z którego przetwarzane jest dowolne wejście (q 0 ∈ Q).
F jest zbiorem stanu / stanów końcowych Q (F ⊆ Q).
Powiązane terminologie
Alfabet
Definition - An alphabet jest dowolnym skończonym zestawem symboli.
Example - ∑ = {a, b, c, d} jest an alphabet set gdzie „a”, „b”, „c” i „d” są symbols.
Strunowy
Definition - A string jest skończonym ciągiem symboli zaczerpniętym z ∑.
Example - „cabcad” jest prawidłowym ciągiem w zestawie alfabetu ∑ = {a, b, c, d}
Długość sznurka
Definition- Jest to liczba symboli obecnych w ciągu. (Oznaczony przez|S|).
Examples -
Jeśli S = 'cabcad', | S | = 6
Jeśli | S | = 0, nazywa się to empty string (Oznaczony przez λ lub ε)
Kleene Star
Definition - Gwiazda Kleene, ∑*, jest operatorem jednoargumentowym na zbiorze symboli lub łańcuchów, ∑, co daje nieskończony zbiór wszystkich możliwych ciągów o wszystkich możliwych długościach ∑ włącznie z λ.
Representation- ∑ * = ∑ 0 ∪ ∑ 1 ∪ ∑ 2 ∪ ……. gdzie ∑ p jest zbiorem wszystkich możliwych ciągów o długości p.
Example - Jeśli ∑ = {a, b}, ∑ * = {λ, a, b, aa, ab, ba, bb, ……… ..}
Zamknięcie Kleene / Plus
Definition - Komplet ∑+ jest nieskończonym zbiorem wszystkich możliwych ciągów o wszystkich możliwych długościach powyżej ∑ z wyłączeniem λ.
Representation- ∑ + = ∑ 1 ∪ ∑ 2 ∪ ∑ 3 ∪ …….
∑ + = ∑ * - {λ}
Example- Jeśli ∑ = {a, b}, ∑ + = {a, b, aa, ab, ba, bb, ……… ..}
Język
Definition- Język to podzbiór ∑ * dla jakiegoś alfabetu ∑. Może być skończona lub nieskończona.
Example - Jeśli język przyjmuje wszystkie możliwe ciągi o długości 2 ponad ∑ = {a, b}, to L = {ab, aa, ba, bb}
Finite Automaton można podzielić na dwa typy -
- Deterministyczny automat skończony (DFA)
- Niedeterministyczny automat skończony (NDFA / NFA)
Deterministyczny automat skończony (DFA)
W DFA dla każdego symbolu wejściowego można określić stan, do którego maszyna się przejdzie. Stąd to się nazywaDeterministic Automaton. Ponieważ ma skończoną liczbę stanów, nazywana jest maszynąDeterministic Finite Machine lub Deterministic Finite Automaton.
Formalna definicja DFA
DFA można przedstawić jako 5-krotkę (Q, ∑, δ, q 0 , F), gdzie -
Q jest skończonym zbiorem stanów.
∑ jest skończonym zbiorem symboli zwanym alfabetem.
δ jest funkcją przejścia, gdzie δ: Q × ∑ → Q
q0jest stanem początkowym, z którego przetwarzane jest dowolne wejście (q 0 ∈ Q).
F jest zbiorem stanu / stanów końcowych Q (F ⊆ Q).
Graficzna reprezentacja DFA
DFA jest reprezentowane przez digrafy zwane state diagram.
- Wierzchołki reprezentują stany.
- Łuki oznaczone alfabetem wejściowym pokazują przejścia.
- Stan początkowy jest oznaczony pustym pojedynczym łukiem wejściowym.
- Stan końcowy jest oznaczony podwójnymi kółkami.
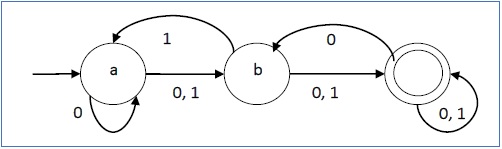
Przykład
Niech deterministyczny automat skończony będzie →
- Q = {a, b, c},
- ∑ = {0, 1},
- q 0 = {a},
- F = {c} i
Funkcja przejścia δ, jak pokazano w poniższej tabeli -
| Stan obecny | Następny stan dla wejścia 0 | Następny stan dla wejścia 1 |
|---|---|---|
| a | za | b |
| b | do | za |
| c | b | do |
Jego graficzna reprezentacja byłaby następująca -

W NDFA, dla określonego symbolu wejściowego, maszyna może przejść do dowolnej kombinacji stanów w maszynie. Innymi słowy, nie można określić dokładnego stanu, do którego porusza się maszyna. Stąd to się nazywaNon-deterministic Automaton. Ponieważ ma skończoną liczbę stanów, nazywana jest maszynąNon-deterministic Finite Machine lub Non-deterministic Finite Automaton.
Formalna definicja NDFA
NDFA można przedstawić jako 5-krotkę (Q, ∑, δ, q 0 , F), gdzie -
Q jest skończonym zbiorem stanów.
∑ jest skończonym zbiorem symboli zwanych alfabetami.
δjest funkcją przejścia, gdzie δ: Q × ∑ → 2 Q
(Tutaj przyjęto zestaw mocy Q (2 Q ), ponieważ w przypadku NDFA ze stanu może nastąpić przejście do dowolnej kombinacji stanów Q)
q0jest stanem początkowym, z którego przetwarzane jest dowolne wejście (q 0 ∈ Q).
F jest zbiorem stanu / stanów końcowych Q (F ⊆ Q).
Graficzna reprezentacja NDFA: (tak samo jak DFA)
NDFA jest reprezentowane przez digrafy zwane diagramem stanów.
- Wierzchołki reprezentują stany.
- Łuki oznaczone alfabetem wejściowym pokazują przejścia.
- Stan początkowy jest oznaczony pustym pojedynczym łukiem wejściowym.
- Stan końcowy jest oznaczony podwójnymi kółkami.
Example
Niech niedeterministyczny automat skończony będzie →
- Q = {a, b, c}
- ∑ = {0, 1}
- q 0 = {a}
- F = {c}
Funkcja przejścia δ, jak pokazano poniżej -
| Stan obecny | Następny stan dla wejścia 0 | Następny stan dla wejścia 1 |
|---|---|---|
| za | a, b | b |
| b | do | a, c |
| do | pne | do |
Jego graficzna reprezentacja byłaby następująca -
DFA vs NDFA
W poniższej tabeli wymieniono różnice między usługami DFA i NDFA.
| DFA | NDFA |
|---|---|
| Przejście ze stanu następuje do jednego określonego następnego stanu dla każdego symbolu wejściowego. Dlatego nazywa się to deterministycznym . | Przejście ze stanu może następować do wielu następnych stanów dla każdego symbolu wejściowego. Dlatego nazywa się to niedeterministycznym . |
| Puste przejścia ciągów nie są widoczne w DFA. | NDFA zezwala na przejścia pustych ciągów. |
| Wycofywanie jest dozwolone w DFA | W NDFA cofanie się nie zawsze jest możliwe. |
| Wymaga więcej miejsca. | Zajmuje mniej miejsca. |
| Ciąg jest akceptowany przez DFA, jeśli przechodzi do stanu końcowego. | Ciąg jest akceptowany przez NDFA, jeśli przynajmniej jedno ze wszystkich możliwych przejść kończy się w stanie końcowym. |
Akceptory, klasyfikatory i przetworniki
Akceptor (rozpoznający)
Automat obliczający funkcję boolowską nazywa się acceptor. Wszystkie stany akceptora albo akceptują, albo odrzucają dane wejściowe.
Klasyfikator
ZA classifier ma więcej niż dwa stany końcowe i daje pojedyncze wyjście po zakończeniu.
Transduktor
Automat, który generuje dane wyjściowe na podstawie bieżącego wejścia i / lub poprzedniego stanu, nazywa się a transducer. Przetworniki mogą być dwojakiego rodzaju -
Mealy Machine - Wyjście zależy zarówno od aktualnego stanu, jak i aktualnego wejścia.
Moore Machine - Wyjście zależy tylko od aktualnego stanu.
Dopuszczalność przez DFA i NDFA
Ciąg jest akceptowany przez DFA / NDFA, jeśli DFA / NDFA rozpoczynający się w stanie początkowym kończy się stanem akceptacji (dowolnym ze stanów końcowych) po całkowitym przeczytaniu ciągu.
Ciąg S jest akceptowany przez DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S) ∈ F
Język L akceptowane przez DFA / NDFA
{S | S ∈ ∑* and δ*(q0, S) ∈ F}
Ciąg S ′ nie jest akceptowany przez DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S′) ∉ F
Językiem L 'nieakceptowanym przez DFA / NDFA (Uzupełnienie akceptowanego języka L) jest
{S | S ∈ ∑* and δ*(q0, S) ∉ F}
Example
Rozważmy DFA pokazane na rysunku 1.3. Z DFA można wyprowadzić dopuszczalne ciągi.

Ciągi akceptowane przez powyższy DFA: {0, 00, 11, 010, 101, ...........}
Ciągi nieakceptowane przez powyższą usługę DFA: {1, 011, 111, ........}
Stwierdzenie problemu
Pozwolić X = (Qx, ∑, δx, q0, Fx)być NDFA, który akceptuje język L (X). Musimy zaprojektować równoważny DFAY = (Qy, ∑, δy, q0, Fy) takie że L(Y) = L(X). Poniższa procedura konwertuje NDFA na jego odpowiednik DFA -
Algorytm
Input - NDFA
Output - Odpowiednik DFA
Step 1 - Utwórz tabelę stanów z podanego NDFA.
Step 2 - Utwórz pustą tabelę stanów pod możliwymi alfabetami wejściowymi dla równoważnego DFA.
Step 3 - Oznacz stan początkowy DFA przez q0 (tak samo jak w przypadku NDFA).
Step 4- Znajdź kombinację stanów {Q 0 , Q 1 , ..., Q n } dla każdego możliwego alfabetu wejściowego.
Step 5 - Za każdym razem, gdy generujemy nowy stan DFA pod kolumnami alfabetu wejściowego, musimy ponownie zastosować krok 4, w przeciwnym razie przejść do kroku 6.
Step 6 - Stany, które zawierają dowolny ze stanów końcowych NDFA, są stanami końcowymi równoważnego DFA.
Przykład
Rozważmy NDFA pokazane na poniższym rysunku.

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| za | {a, b, c, d, e} | {d, e} |
| b | {do} | {mi} |
| do | ∅ | {b} |
| re | {mi} | ∅ |
| mi | ∅ | ∅ |
Korzystając z powyższego algorytmu, znajdujemy jego odpowiednik DFA. Tabela stanów DFA jest pokazana poniżej.
| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| [za] | [a, b, c, d, e] | [d, e] |
| [a, b, c, d, e] | [a, b, c, d, e] | [b, d, e] |
| [d, e] | [mi] | ∅ |
| [b, d, e] | [c, e] | [mi] |
| [mi] | ∅ | ∅ |
| [c, e] | ∅ | [b] |
| [b] | [do] | [mi] |
| [do] | ∅ | [b] |
Schemat stanu DFA jest następujący -

Minimalizacja DFA za pomocą twierdzenia Myhill-Nerode
Algorytm
Input - DFA
Output - Zminimalizowany DFA
Step 1- Narysuj tabelę dla wszystkich par stanów (Q i , Q j ) niekoniecznie połączonych bezpośrednio [Wszystkie są początkowo odznaczone]
Step 2- Rozważ każdą parę stanów (Q i , Q j ) w DFA, gdzie Q i ∈ F i Q j ∉ F lub odwrotnie i zaznacz je. [Tutaj F jest zbiorem stanów końcowych]
Step 3 - Powtarzaj ten krok, dopóki nie będziemy mogli już zaznaczyć stanów -
Jeśli istnieje para nieoznaczona (Q i , Q j ), zaznacz ją, jeśli para {δ (Q i , A), δ (Q i , A)} jest zaznaczona dla jakiegoś alfabetu wejściowego.
Step 4- Połącz wszystkie nieoznakowane pary (Q i , Q j ) i uczyń je jednym stanem w zredukowanym DFA.
Przykład
Użyjmy algorytmu 2, aby zminimalizować DFA pokazane poniżej.

Step 1 - Rysujemy tabelę dla wszystkich par stanów.
| za | b | do | re | mi | fa | |
| za | ||||||
| b | ||||||
| do | ||||||
| re | ||||||
| mi | ||||||
| fa |
Step 2 - Zaznaczamy pary stanów.
| za | b | do | re | mi | fa | |
| za | ||||||
| b | ||||||
| do | ✔ | ✔ | ||||
| re | ✔ | ✔ | ||||
| mi | ✔ | ✔ | ||||
| fa | ✔ | ✔ | ✔ |
Step 3- Postaramy się zaznaczyć przejściowo pary stanów zielonym haczykiem. Jeśli wprowadzimy 1, aby określić stan „a” i „f”, przejdzie on odpowiednio do stanu „c” i „f”. (c, f) jest już zaznaczone, stąd oznaczymy parę (a, f). Teraz wprowadzamy 1, aby określić „b” i „f”; przejdzie odpowiednio do stanu „d” i „f”. (d, f) jest już zaznaczone, stąd oznaczymy parę (b, f).
| za | b | do | re | mi | fa | |
| za | ||||||
| b | ||||||
| do | ✔ | ✔ | ||||
| re | ✔ | ✔ | ||||
| mi | ✔ | ✔ | ||||
| fa | ✔ | ✔ | ✔ | ✔ | ✔ |
Po kroku 3 mamy kombinacje stanów {a, b} {c, d} {c, e} {d, e}, które są nieoznaczone.
Możemy rekombinować {c, d} {c, e} {d, e} w {c, d, e}
Stąd mamy dwa połączone stany jako - {a, b} i {c, d, e}
Więc ostateczny zminimalizowany DFA będzie zawierał trzy stany {f}, {a, b} i {c, d, e}
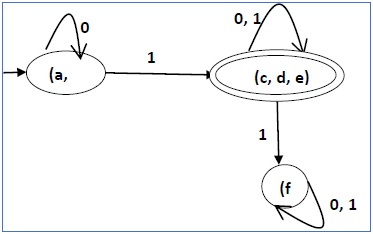
Minimalizacja DFA za pomocą twierdzenia o równoważności
Jeśli X i Y są dwoma stanami w DFA, możemy połączyć te dwa stany w {X, Y}, jeśli nie są rozróżnialne. Można rozróżnić dwa stany, jeśli istnieje co najmniej jeden ciąg S, taki, że jeden z δ (X, S) i δ (Y, S) akceptuje, a drugi nie. W związku z tym DFA jest minimalny wtedy i tylko wtedy, gdy wszystkie stany są rozróżnialne.
Algorytm 3
Step 1 - Wszystkie stany Q są podzielone na dwie partycje - final states i non-final states i są oznaczone P0. Wszystkie stany w partycji są równoważne zeru . Weź licznikk i zainicjuj go wartością 0.
Step 2- Przyrost k o 1. Dla każdego podziału w P k podziel stany w P k na dwie partycje, jeśli są one k-rozróżnialne. Dwa stany w tej partycji X i Y są k-rozróżnialne, jeśli istnieje wejścieS takie że δ(X, S) i δ(Y, S) są (k-1) -distinguishable.
Step 3- Jeśli P k ≠ P k-1 , powtórz krok 2, w przeciwnym razie przejdź do kroku 4.
Step 4- Połącz k- ty równoważne zestawy i uczyń je nowymi stanami zredukowanego DFA.
Przykład
Rozważmy następujący DFA -

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| za | b | do |
| b | za | re |
| do | mi | fa |
| re | mi | fa |
| mi | mi | fa |
| fa | fa | fa |
Zastosujmy powyższy algorytm do powyższego DFA -
- P 0 = {(c, d, e), (a, b, f)}
- P 1 = {(c, d, e), (a, b), (f)}
- P 2 = {(c, d, e), (a, b), (f)}
Stąd P 1 = P 2 .
Istnieją trzy stany w zredukowanym DFA. Obniżony DFA wygląda następująco -
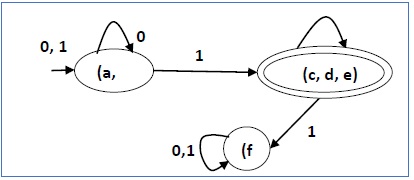
| Q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| (a, b) | (a, b) | (c, d, e) |
| (c, d, e) | (c, d, e) | (fa) |
| (fa) | (fa) | (fa) |
Automaty skończone mogą mieć wyjścia odpowiadające każdemu przejściu. Istnieją dwa typy maszyn o skończonych stanach, które generują dane wyjściowe -
- Mączna Maszyna
- Maszyna Moore'a
Mączna Maszyna
Maszyna Mealy to FSM, którego wyjście zależy od aktualnego stanu, jak również od aktualnego wejścia.
Można to opisać za pomocą 6 krotek (Q, ∑, O, δ, X, q 0 ), gdzie -
Q jest skończonym zbiorem stanów.
∑ jest skończonym zbiorem symboli zwanym alfabetem wejściowym.
O jest skończonym zbiorem symboli zwanym alfabetem wyjściowym.
δ jest funkcją przejścia wejściowego, gdzie δ: Q × ∑ → Q
X jest funkcją przejścia wyjściowego, gdzie X: Q × ∑ → O
q0jest stanem początkowym, z którego przetwarzane jest dowolne wejście (q 0 ∈ Q).
Tabela stanów Mealy Machine jest pokazana poniżej -
| Stan obecny | Następny stan | |||
|---|---|---|---|---|
| wejście = 0 | wejście = 1 | |||
| Stan | Wynik | Stan | Wynik | |
| → a | b | x 1 | do | x 1 |
| b | b | x 2 | re | x 3 |
| do | re | x 3 | do | x 1 |
| re | re | x 3 | re | x 2 |
Schemat stanu powyższej Mealy Machine to -

Moore Machine
Maszyna Moore'a to FSM, którego wyniki zależą tylko od aktualnego stanu.
Maszynę Moore'a można opisać za pomocą 6 krotek (Q, ∑, O, δ, X, q 0 ), gdzie -
Q jest skończonym zbiorem stanów.
∑ jest skończonym zbiorem symboli zwanym alfabetem wejściowym.
O jest skończonym zbiorem symboli zwanym alfabetem wyjściowym.
δ jest funkcją przejścia wejściowego, gdzie δ: Q × ∑ → Q
X jest funkcją przejścia wyjściowego, gdzie X: Q → O
q0jest stanem początkowym, z którego przetwarzane jest dowolne wejście (q 0 ∈ Q).
Tabela stanów maszyny Moore jest pokazana poniżej -
| Stan obecny | Następny stan | Wynik | |
|---|---|---|---|
| Wejście = 0 | Wejście = 1 | ||
| → a | b | do | x 2 |
| b | b | re | x 1 |
| do | do | re | x 2 |
| re | re | re | x 3 |
Schemat stanu powyższej Maszyny Moore to -

Mealy Machine vs Moore Machine
Poniższa tabela podkreśla punkty, które odróżniają maszynę Mealy od maszyny Moore.
| Mączna Maszyna | Moore Machine |
|---|---|
| Wyjście zależy zarówno od aktualnego stanu, jak i aktualnego wejścia | Wynik zależy tylko od aktualnego stanu. |
| Generalnie ma mniej stanów niż Moore Machine. | Generalnie ma więcej stanów niż Mealy Machine. |
| Wartość funkcji wyjściowej jest funkcją przejść i zmian, gdy logika wejściowa jest zakończona. | Wartość funkcji wyjściowej jest funkcją aktualnego stanu i zmian na zboczach zegara, gdy zachodzą zmiany stanu. |
| Maszyny Mealy szybciej reagują na dane wejściowe. Na ogół reagują w tym samym cyklu zegara. | W maszynach Moore'a potrzeba więcej logiki do dekodowania wyjść, co skutkuje większą liczbą opóźnień obwodów. Zwykle reagują o jeden cykl zegara później. |
Moore Machine to Mealy Machine
Algorytm 4
Input - Maszyna Moore'a
Output - Maszyna Mączna
Step 1 - Weź pusty format tabeli przejścia Mealy Machine.
Step 2 - Skopiuj wszystkie stany przejścia Moore Machine do tego formatu tabeli.
Step 3- Sprawdź obecne stany i odpowiadające im wyjścia w tabeli stanów Maszyny Moore'a; jeśli dla stanu Q i wyjście jest m, skopiuj je do kolumn wyjściowych tabeli stanów Mealy Machine, gdziekolwiek Q i pojawi się w następnym stanie.
Przykład
Rozważmy następującą maszynę Moore'a -
| Stan obecny | Następny stan | Wynik | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → a | re | b | 1 |
| b | za | re | 0 |
| do | do | do | 0 |
| re | b | za | 1 |
Teraz stosujemy algorytm 4, aby przekonwertować go na Mealy Machine.
Step 1 & 2 -
| Stan obecny | Następny stan | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Stan | Wynik | Stan | Wynik | |
| → a | re | b | ||
| b | za | re | ||
| do | do | do | ||
| re | b | za | ||
Step 3 -
| Stan obecny | Następny stan | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Stan | Wynik | Stan | Wynik | |
| => a | re | 1 | b | 0 |
| b | za | 1 | re | 1 |
| do | do | 0 | do | 0 |
| re | b | 0 | za | 1 |
Mealy Machine to Moore Machine
Algorytm 5
Input - Maszyna Mączna
Output - Maszyna Moore'a
Step 1- Oblicz liczbę różnych wyjść dla każdego stanu (Q i ), które są dostępne w tabeli stanów maszyny Mealy.
Step 2- Jeśli wszystkie wyjścia Qi są takie same, skopiuj stan Q i . Jeśli ma n różnych wyjść, przerwy P I do n stanów jako Q w którymn = 0, 1, 2 .......
Step 3 - Jeśli wyjście stanu początkowego ma wartość 1, wstaw nowy stan początkowy na początku, który daje wyjście 0.
Przykład
Rozważmy następującą Mealy Machine -
| Stan obecny | Następny stan | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Następny stan | Wynik | Następny stan | Wynik | |
| → a | re | 0 | b | 1 |
| b | za | 1 | re | 0 |
| do | do | 1 | do | 0 |
| re | b | 0 | za | 1 |
Tutaj stany „a” i „d” dają odpowiednio tylko 1 i 0 wyjść, więc zachowujemy stany „a” i „d”. Ale stany „b” i „c” dają różne wyniki (1 i 0). Więc dzielimy sięb w b0, b1 i c w c0, c1.
| Stan obecny | Następny stan | Wynik | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → a | re | b 1 | 1 |
| b 0 | za | re | 0 |
| b 1 | za | re | 1 |
| c 0 | c 1 | C 0 | 0 |
| c 1 | c 1 | C 0 | 1 |
| re | b 0 | za | 0 |
W sensie literackim tego terminu gramatyki oznaczają reguły składniowe konwersacji w językach naturalnych. Lingwistyka próbowała zdefiniować gramatyki od czasu powstania języków naturalnych, takich jak angielski, sanskryt, mandaryński itp.
Teoria języków formalnych znajduje szerokie zastosowanie w dziedzinie informatyki. Noam Chomsky przedstawił matematyczny model gramatyki w 1956 roku, który jest skuteczny w pisaniu języków komputerowych.
Gramatyka
Gramatyka G można formalnie zapisać jako 4-krotkę (N, T, S, P), gdzie -
N lub VN jest zbiorem zmiennych lub symboli nieterminalnych.
T lub ∑ to zestaw symboli terminala.
S to specjalna zmienna nazywana symbolem Start, S ∈ N
Pto Zasady produkcji dla terminali i terminali. Zasada produkcja ma postać α → p, gdzie α i β są struny V N ∪ Ď i co najmniej jeden symbol α należy do V N .
Przykład
Gramatyka G1 -
({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})
Tutaj,
S, A, i B są symbolami nieterminowymi;
a i b to symbole terminala
S to symbol startu, S ∈ N
Produkcje, P : S → AB, A → a, B → b
Przykład
Gramatyka G2 -
(({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Tutaj,
S i A są symbolami nieterminowymi.
a i b to symbole terminala.
ε jest pustym ciągiem.
S to symbol startu, S ∈ N
Produkcja P : S → aAb, aA → aaAb, A → ε
Wyprowadzenia z gramatyki
Łańcuchy mogą pochodzić z innych ciągów przy użyciu produkcji w gramatyce. Jeśli gramatykaG ma produkcję α → β, możemy to powiedzieć x α y pochodzi x β y w G. To wyprowadzenie jest zapisane jako -
x α y ⇒G x β y
Przykład
Rozważmy gramatykę -
G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Niektóre z ciągów, które można wyprowadzić, to:
S ⇒ aA b używając produkcji S → aAb
⇒ a aA bb używając produkcji aA → aAb
⇒ aaa A bbb przy użyciu produkcji aA → aAb
⇒ aaabbb używając produkcji A → ε
Zbiór wszystkich ciągów, które można wyprowadzić z gramatyki, nazywany jest językiem wygenerowanym na podstawie tej gramatyki. Język generowany przez gramatykęG jest podzbiorem formalnie zdefiniowanym przez
L (G) = {W | W ∈ ∑ *, S ⇒ G W }
Gdyby L(G1) = L(G2), Gramatyka G1 jest odpowiednikiem gramatyki G2.
Przykład
Jeśli jest gramatyka
G: N = {S, A, B} T = {a, b} P = {S → AB, A → a, B → b}
Tutaj S produkuje ABi możemy wymienić A przez a, i B przez b. Tutaj jedynym akceptowanym ciągiem jestabtj.
L (G) = {ab}
Przykład
Załóżmy, że mamy następującą gramatykę -
G: N = {S, A, B} T = {a, b} P = {S → AB, A → aA | a, B → bB | b}
Język wygenerowany przez tę gramatykę -
L (G) = {ab, a 2 b, ab 2 , a 2 b 2 , ………}
= {a m b n | m ≥ 1 in ≥ 1}
Konstrukcja gramatyki generującej język
Rozważymy niektóre języki i przekonwertujemy je na gramatykę G, która tworzy te języki.
Przykład
Problem- Załóżmy, że L (G) = {a m b n | m ≥ 0 in> 0}. Musimy poznać gramatykęG który produkuje L(G).
Solution
Ponieważ L (G) = {a m b n | m ≥ 0 in> 0}
zbiór zaakceptowanych ciągów można przepisać jako -
L (G) = {b, ab, bb, aab, abb, …….}
W tym przypadku symbol początkowy musi mieć co najmniej jedno „b” poprzedzone dowolną liczbą „a”, w tym zero.
Aby zaakceptować zestaw ciągów {b, ab, bb, aab, abb, …….}, Wzięliśmy produkcje -
S → aS, S → B, B → b i B → bB
S → B → b (zaakceptowano)
S → B → bB → bb (zaakceptowano)
S → aS → aB → ab (zaakceptowano)
S → aS → aaS → aaB → aab (zaakceptowano)
S → aS → aB → abB → abb (Zaakceptowano)
W ten sposób możemy udowodnić, że każdy pojedynczy ciąg w L (G) jest akceptowany przez język generowany przez zbiór produkcyjny.
Stąd gramatyka -
G: ({S, A, B}, {a, b}, S, {S → aS | B, B → b | bB})
Przykład
Problem- Załóżmy, że L (G) = {a m b n | m> 0 i n ≥ 0}. Musimy znaleźć gramatykę G, która daje L (G).
Solution -
Ponieważ L (G) = {a m b n | m> 0 in ≥ 0}, zbiór akceptowanych ciągów można przepisać jako -
L (G) = {a, aa, ab, aaa, aab, abb, …….}
W tym przypadku symbol początkowy musi mieć co najmniej jedno „a”, po którym następuje dowolna liczba „b”, w tym null.
Aby zaakceptować zestaw ciągów {a, aa, ab, aaa, aab, abb, …….}, Wzięliśmy produkcje -
S → aA, A → aA, A → B, B → bB, B → λ
S → aA → aB → aλ → a (zaakceptowano)
S → aA → aaA → aaB → aaλ → aa (zaakceptowano)
S → aA → aB → abB → abλ → ab (zaakceptowano)
S → aA → aaA → aaaA → aaaB → aaaλ → aaa (zaakceptowano)
S → aA → aaA → aaB → aabB → aabλ → aab (zaakceptowano)
S → aA → aB → abB → abbB → abbλ → abb (zaakceptowano)
W ten sposób możemy udowodnić, że każdy pojedynczy ciąg w L (G) jest akceptowany przez język generowany przez zbiór produkcyjny.
Stąd gramatyka -
G: ({S, A, B}, {a, b}, S, {S → aA, A → aA | B, B → λ | bB})
Według Noama Chomosky'ego istnieją cztery typy gramatyki - typ 0, typ 1, typ 2 i typ 3. Poniższa tabela przedstawia różnice między nimi -
| Typ gramatyki | Zaakceptowano gramatykę | Zaakceptowano język | Automat |
|---|---|---|---|
| Wpisz 0 | Nieograniczona gramatyka | Język rekurencyjnie wyliczalny | Maszyna Turinga |
| Typ 1 | Gramatyka kontekstowa | Język wrażliwy na kontekst | Automat z ograniczeniami liniowymi |
| Wpisz 2 | Gramatyka bezkontekstowa | Język bezkontekstowy | Automat dociskowy |
| Type 3 | Regular grammar | Regular language | Finite state automaton |
Take a look at the following illustration. It shows the scope of each type of grammar −

Type - 3 Grammar
Type-3 grammars generate regular languages. Type-3 grammars must have a single non-terminal on the left-hand side and a right-hand side consisting of a single terminal or single terminal followed by a single non-terminal.
The productions must be in the form X → a or X → aY
where X, Y ∈ N (Non terminal)
and a ∈ T (Terminal)
The rule S → ε is allowed if S does not appear on the right side of any rule.
Example
X → ε
X → a | aY
Y → bType - 2 Grammar
Type-2 grammars generate context-free languages.
The productions must be in the form A → γ
where A ∈ N (Non terminal)
and γ ∈ (T ∪ N)* (String of terminals and non-terminals).
These languages generated by these grammars are be recognized by a non-deterministic pushdown automaton.
Example
S → X a
X → a
X → aX
X → abc
X → εType - 1 Grammar
Type-1 grammars generate context-sensitive languages. The productions must be in the form
α A β → α γ β
where A ∈ N (Non-terminal)
and α, β, γ ∈ (T ∪ N)* (Strings of terminals and non-terminals)
The strings α and β may be empty, but γ must be non-empty.
The rule S → ε is allowed if S does not appear on the right side of any rule. The languages generated by these grammars are recognized by a linear bounded automaton.
Example
AB → AbBc
A → bcA
B → bType - 0 Grammar
Type-0 grammars generate recursively enumerable languages. The productions have no restrictions. They are any phase structure grammar including all formal grammars.
They generate the languages that are recognized by a Turing machine.
The productions can be in the form of α → β where α is a string of terminals and nonterminals with at least one non-terminal and α cannot be null. β is a string of terminals and non-terminals.
Example
S → ACaB
Bc → acB
CB → DB
aD → DbA Regular Expression can be recursively defined as follows −
ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
φ is a Regular Expression denoting an empty language. (L (φ) = { })
x is a Regular Expression where L = {x}
If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then
X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y).
X . Y is a Regular Expression corresponding to the language L(X) . L(Y) where L(X.Y) = L(X) . L(Y)
R* is a Regular Expression corresponding to the language L(R*)where L(R*) = (L(R))*
If we apply any of the rules several times from 1 to 5, they are Regular Expressions.
Some RE Examples
| Regular Expressions | Regular Set |
|---|---|
| (0 + 10*) | L = { 0, 1, 10, 100, 1000, 10000, … } |
| (0*10*) | L = {1, 01, 10, 010, 0010, …} |
| (0 + ε)(1 + ε) | L = {ε, 0, 1, 01} |
| (a+b)* | Set of strings of a’s and b’s of any length including the null string. So L = { ε, a, b, aa , ab , bb , ba, aaa…….} |
| (a+b)*abb | Set of strings of a’s and b’s ending with the string abb. So L = {abb, aabb, babb, aaabb, ababb, …………..} |
| (11)* | Set consisting of even number of 1’s including empty string, So L= {ε, 11, 1111, 111111, ……….} |
| (aa)*(bb)*b | Set of strings consisting of even number of a’s followed by odd number of b’s , so L = {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, …………..} |
| (aa + ab + ba + bb)* | String of a’s and b’s of even length can be obtained by concatenating any combination of the strings aa, ab, ba and bb including null, so L = {aa, ab, ba, bb, aaab, aaba, …………..} |
Any set that represents the value of the Regular Expression is called a Regular Set.
Properties of Regular Sets
Property 1. The union of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(aa)* and RE2 = (aa)*
So, L1 = {a, aaa, aaaaa,.....} (Strings of odd length excluding Null)
and L2 ={ ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,.......}
(Strings of all possible lengths including Null)
RE (L1 ∪ L2) = a* (which is a regular expression itself)
Hence, proved.
Property 2. The intersection of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(a*) and RE2 = (aa)*
So, L1 = { a,aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∩ L2 = { aa, aaaa, aaaaaa,.......} (Strings of even length excluding Null)
RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.
Hence, proved.
Property 3. The complement of a regular set is regular.
Proof −
Let us take a regular expression −
RE = (aa)*
So, L = {ε, aa, aaaa, aaaaaa, .......} (Strings of even length including Null)
Complement of L is all the strings that is not in L.
So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)
RE (L’) = a(aa)* which is a regular expression itself.
Hence, proved.
Property 4. The difference of two regular set is regular.
Proof −
Let us take two regular expressions −
RE1 = a (a*) and RE2 = (aa)*
So, L1 = {a, aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}
(Strings of all odd lengths excluding Null)
RE (L1 – L2) = a (aa)* which is a regular expression.
Hence, proved.
Property 5. The reversal of a regular set is regular.
Proof −
We have to prove LR is also regular if L is a regular set.
Let, L = {01, 10, 11, 10}
RE (L) = 01 + 10 + 11 + 10
LR = {10, 01, 11, 01}
RE (LR) = 01 + 10 + 11 + 10 which is regular
Hence, proved.
Property 6. The closure of a regular set is regular.
Proof −
If L = {a, aaa, aaaaa, .......} (Strings of odd length excluding Null)
i.e., RE (L) = a (aa)*
L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)
RE (L*) = a (a)*
Hence, proved.
Property 7. The concatenation of two regular sets is regular.
Proof −
Let RE1 = (0+1)*0 and RE2 = 01(0+1)*
Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)
and L2 = {01, 010,011,.....} (Set of strings beginning with 01)
Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*
Hence, proved.
Identities Related to Regular Expressions
Given R, P, L, Q as regular expressions, the following identities hold −
- ∅* = ε
- ε* = ε
- RR* = R*R
- R*R* = R*
- (R*)* = R*
- RR* = R*R
- (PQ)*P =P(QP)*
- (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
- R + ∅ = ∅ + R = R (The identity for union)
- R ε = ε R = R (The identity for concatenation)
- ∅ L = L ∅ = ∅ (The annihilator for concatenation)
- R + R = R (Idempotent law)
- L (M + N) = LM + LN (Left distributive law)
- (M + N) L = ML + NL (Right distributive law)
- ε + RR* = ε + R*R = R*
In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.
Statement −
Let P and Q be two regular expressions.
If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*
Proof −
R = Q + (Q + RP)P [After putting the value R = Q + RP]
= Q + QP + RPP
When we put the value of R recursively again and again, we get the following equation −
R = Q + QP + QP2 + QP3…..
R = Q (ε + P + P2 + P3 + …. )
R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]
Hence, proved.
Assumptions for Applying Arden’s Theorem
- The transition diagram must not have NULL transitions
- It must have only one initial state
Method
Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q1.
q1 = q1R11 + q2R21 + … + qnRn1 + ε
q2 = q1R12 + q2R22 + … + qnRn2
…………………………
…………………………
…………………………
…………………………
qn = q1R1n + q2R2n + … + qnRnn
Rij represents the set of labels of edges from qi to qj, if no such edge exists, then Rij = ∅
Step 2 − Solve these equations to get the equation for the final state in terms of Rij
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state and final state is q1.
The equations for the three states q1, q2, and q3 are as follows −
q1 = q1a + q3a + ε (ε move is because q1 is the initial state0
q2 = q1b + q2b + q3b
q3 = q2a
Now, we will solve these three equations −
q2 = q1b + q2b + q3b
= q1b + q2b + (q2a)b (Substituting value of q3)
= q1b + q2(b + ab)
= q1b (b + ab)* (Applying Arden’s Theorem)
q1 = q1a + q3a + ε
= q1a + q2aa + ε (Substituting value of q3)
= q1a + q1b(b + ab*)aa + ε (Substituting value of q2)
= q1(a + b(b + ab)*aa) + ε
= ε (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
Hence, the regular expression is (a + b(b + ab)*aa)*.
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state is q1 and the final state is q2
Now we write down the equations −
q1 = q10 + ε
q2 = q11 + q20
q3 = q21 + q30 + q31
Now, we will solve these three equations −
q1 = ε0* [As, εR = R]
So, q1 = 0*
q2 = 0*1 + q20
So, q2 = 0*1(0)* [By Arden’s theorem]
Hence, the regular expression is 0*10*.
We can use Thompson's Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.
Some basic RA expressions are the following −
Case 1 − For a regular expression ‘a’, we can construct the following FA −

Case 2 − For a regular expression ‘ab’, we can construct the following FA −

Case 3 − For a regular expression (a+b), we can construct the following FA −

Case 4 − For a regular expression (a+b)*, we can construct the following FA −

Method
Step 1 Construct an NFA with Null moves from the given regular expression.
Step 2 Remove Null transition from the NFA and convert it into its equivalent DFA.
Problem
Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0
Solution
We will concatenate three expressions "1", "(0 + 1)*" and "0"

Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −

It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.
Finite Automata with Null Moves (NFA-ε)
A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move.
An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q0, F), consisting of
Q − a finite set of states
∑ − a finite set of input symbols
δ − a transition function δ : Q × (∑ ∪ {ε}) → 2Q
q0 − an initial state q0 ∈ Q
F − a set of final state/states of Q (F⊆Q).

The above (FA-ε) accepts a string set − {0, 1, 01}
Removal of Null Moves from Finite Automata
If in an NDFA, there is ϵ-move between vertex X to vertex Y, we can remove it using the following steps −
- Find all the outgoing edges from Y.
- Copy all these edges starting from X without changing the edge labels.
- If X is an initial state, make Y also an initial state.
- If Y is a final state, make X also a final state.
Problem
Convert the following NFA-ε to NFA without Null move.

Solution
Step 1 −
Here the ε transition is between q1 and q2, so let q1 is X and qf is Y.
Here the outgoing edges from qf is to qf for inputs 0 and 1.
Step 2 −
Now we will Copy all these edges from q1 without changing the edges from qf and get the following FA −

Step 3 −
Here q1 is an initial state, so we make qf also an initial state.
So the FA becomes −

Step 4 −
Here qf is a final state, so we make q1 also a final state.
So the FA becomes −

Theorem
Let L be a regular language. Then there exists a constant ‘c’ such that for every string w in L −
|w| ≥ c
We can break w into three strings, w = xyz, such that −
- |y| > 0
- |xy| ≤ c
- For all k ≥ 0, the string xykz is also in L.
Applications of Pumping Lemma
Pumping Lemma is to be applied to show that certain languages are not regular. It should never be used to show a language is regular.
If L is regular, it satisfies Pumping Lemma.
If L does not satisfy Pumping Lemma, it is non-regular.
Method to prove that a language L is not regular
At first, we have to assume that L is regular.
So, the pumping lemma should hold for L.
Use the pumping lemma to obtain a contradiction −
Select w such that |w| ≥ c
Select y such that |y| ≥ 1
Select x such that |xy| ≤ c
Assign the remaining string to z.
Select k such that the resulting string is not in L.
Hence L is not regular.
Problem
Prove that L = {aibi | i ≥ 0} is not regular.
Solution −
At first, we assume that L is regular and n is the number of states.
Let w = anbn. Thus |w| = 2n ≥ n.
By pumping lemma, let w = xyz, where |xy| ≤ n.
Let x = ap, y = aq, and z = arbn, where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
Let k = 2. Then xy2z = apa2qarbn.
Number of as = (p + 2q + r) = (p + q + r) + q = n + q
Hence, xy2z = an+q bn. Since q ≠ 0, xy2z is not of the form anbn.
Thus, xy2z is not in L. Hence L is not regular.
If (Q, ∑, δ, q0, F) be a DFA that accepts a language L, then the complement of the DFA can be obtained by swapping its accepting states with its non-accepting states and vice versa.
We will take an example and elaborate this below −

This DFA accepts the language
L = {a, aa, aaa , ............. }
over the alphabet
∑ = {a, b}
So, RE = a+.
Now we will swap its accepting states with its non-accepting states and vice versa and will get the following −

This DFA accepts the language
Ľ = {ε, b, ab ,bb,ba, ............... }
over the alphabet
∑ = {a, b}
Note − If we want to complement an NFA, we have to first convert it to DFA and then have to swap states as in the previous method.
Definition − A context-free grammar (CFG) consisting of a finite set of grammar rules is a quadruple (N, T, P, S) where
N is a set of non-terminal symbols.
T is a set of terminals where N ∩ T = NULL.
P is a set of rules, P: N → (N ∪ T)*, i.e., the left-hand side of the production rule P does have any right context or left context.
S is the start symbol.
Example
- The grammar ({A}, {a, b, c}, P, A), P : A → aA, A → abc.
- The grammar ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
- The grammar ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Generation of Derivation Tree
A derivation tree or parse tree is an ordered rooted tree that graphically represents the semantic information a string derived from a context-free grammar.
Representation Technique
Root vertex − Must be labeled by the start symbol.
Vertex − Labeled by a non-terminal symbol.
Leaves − Labeled by a terminal symbol or ε.
If S → x1x2 …… xn is a production rule in a CFG, then the parse tree / derivation tree will be as follows −

There are two different approaches to draw a derivation tree −
Top-down Approach −
Starts with the starting symbol S
Goes down to tree leaves using productions
Bottom-up Approach −
Starts from tree leaves
Proceeds upward to the root which is the starting symbol S
Derivation or Yield of a Tree
The derivation or the yield of a parse tree is the final string obtained by concatenating the labels of the leaves of the tree from left to right, ignoring the Nulls. However, if all the leaves are Null, derivation is Null.
Example
Let a CFG {N,T,P,S} be
N = {S}, T = {a, b}, Starting symbol = S, P = S → SS | aSb | ε
One derivation from the above CFG is “abaabb”
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Sentential Form and Partial Derivation Tree
A partial derivation tree is a sub-tree of a derivation tree/parse tree such that either all of its children are in the sub-tree or none of them are in the sub-tree.
Example
If in any CFG the productions are −
S → AB, A → aaA | ε, B → Bb| ε
the partial derivation tree can be the following −
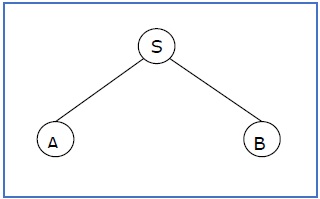
If a partial derivation tree contains the root S, it is called a sentential form. The above sub-tree is also in sentential form.
Leftmost and Rightmost Derivation of a String
Leftmost derivation − A leftmost derivation is obtained by applying production to the leftmost variable in each step.
Rightmost derivation − A rightmost derivation is obtained by applying production to the rightmost variable in each step.
Example
Let any set of production rules in a CFG be
X → X+X | X*X |X| a
over an alphabet {a}.
The leftmost derivation for the string "a+a*a" may be −
X → X+X → a+X → a + X*X → a+a*X → a+a*a
Krokowe wyprowadzenie powyższego ciągu jest pokazane poniżej -

Najbardziej prawe wyprowadzenie powyższego ciągu "a+a*a" może być -
X → X * X → X * a → X + X * a → X + a * a → a + a * a
Krokowe wyprowadzenie powyższego ciągu jest pokazane poniżej -

Gramatyki rekurencyjne dla lewej i prawej strony
W gramatyce bezkontekstowej G, jeśli w formularzu jest produkcja X → Xa gdzie X nie jest terminalem i ‘a’ jest ciągiem terminali, nazywa się a left recursive production. Gramatyka z lewostronną produkcją rekurencyjną nazywa się aleft recursive grammar.
A jeśli w gramatyce bezkontekstowej G, jeśli jest produkcja w formie X → aX gdzie X nie jest terminalem i ‘a’ jest ciągiem terminali, nazywa się a right recursive production. Gramatyka mająca odpowiednią rekurencyjną produkcję nazywa się aright recursive grammar.
Jeśli gramatyka bezkontekstowa G ma więcej niż jedno drzewo pochodne dla danego łańcucha w ∈ L(G), to się nazywa ambiguous grammar. Istnieje wiele wyprowadzeń z prawej lub lewej strony dla jakiegoś napisu wygenerowanego na podstawie tej gramatyki.
Problem
Sprawdź, czy gramatyka G z regułami produkcji -
X → X + X | X * X | X | za
jest niejednoznaczna, czy nie.
Rozwiązanie
Znajdźmy drzewo pochodne dla łańcucha „a + a * a”. Ma dwie skrajne lewe wyprowadzenia.
Derivation 1- X → X + X → a + X → a + X * X → a + a * X → a + a * a
Parse tree 1 -

Derivation 2- X → X * X → X + X * X → a + X * X → a + a * X → a + a * a
Parse tree 2 -

Ponieważ istnieją dwa drzewa parsowania dla pojedynczego łańcucha „a + a * a”, gramatyka G jest dwuznaczny.
Języki bezkontekstowe to closed poniżej -
- Union
- Concatenation
- Operacja Kleene Star
Unia
Niech L 1 i L 2 będą dwoma językami bezkontekstowymi. Wtedy L 1 ∪ L 2 jest również bezkontekstowa.
Przykład
Niech L 1 = {a n b n , n> 0}. Odpowiednia gramatyka G 1 będzie miała P: S1 → aAb | ab
Niech L 2 = {c m d m , m ≥ 0}. Odpowiednia gramatyka G 2 będzie miała P: S2 → cBb | ε
Połączenie L 1 i L 2 , L = L 1 ∪ L 2 = {a n b n } ∪ {c m d m }
Odpowiednia gramatyka G będzie miała dodatkową produkcję S → S1 | S2
Powiązanie
Jeśli L 1 i L 2 są językami bezkontekstowymi, to L 1 L 2 jest również bezkontekstowe.
Przykład
Unia języków L 1 i L 2 , L = L 1 L 2 = {a n b n c m d m }
Odpowiednia gramatyka G będzie miała dodatkową produkcję S → S1 S2
Kleene Star
Jeśli L jest językiem bezkontekstowym, to L * jest również bezkontekstowy.
Przykład
Niech L = {a n b n , n ≥ 0}. Odpowiednia gramatyka G będzie miała P: S → aAb | ε
Kleene Star L 1 = {a n b n } *
Odpowiednia gramatyka G 1 będzie miała dodatkowe produkcje S1 → SS 1 | ε
Języki bezkontekstowe to not closed poniżej -
Intersection - Jeśli L1 i L2 są językami bezkontekstowymi, to L1 ∩ L2 niekoniecznie są bezkontekstowe.
Intersection with Regular Language - Jeśli L1 jest językiem zwykłym, a L2 jest językiem bezkontekstowym, to L1 ∩ L2 jest językiem bezkontekstowym.
Complement - Jeśli L1 jest językiem bezkontekstowym, to L1 'może nie być bezkontekstowy.
W CFG może się zdarzyć, że wszystkie reguły produkcji i symbole nie są potrzebne do wyprowadzenia łańcuchów. Poza tym mogą istnieć produkcje zerowe i jednostkowe. Eliminacja tych produkcji i symboli nazywa sięsimplification of CFGs. Uproszczenie składa się zasadniczo z następujących kroków -
- Redukcja CFG
- Usunięcie produkcji jednostkowej
- Usunięcie Null Productions
Redukcja CFG
CFG są redukowane w dwóch fazach -
Phase 1 - wyprowadzenie równoważnej gramatyki, G’z CFG, G, tak, że każda zmienna wyprowadza jakiś ciąg terminala.
Derivation Procedure -
Krok 1 - Uwzględnij wszystkie symbole, W1, które wyprowadzają jakiś terminal i inicjalizują i=1.
Krok 2 - Uwzględnij wszystkie symbole, Wi+1, które pochodzą Wi.
Krok 3 - Przyrost i i powtórz krok 2, aż Wi+1 = Wi.
Krok 4 - Uwzględnij wszystkie reguły produkcji, które mają Wi w tym.
Phase 2 - wyprowadzenie równoważnej gramatyki, G”z CFG, G’tak, że każdy symbol pojawia się w formie zdaniowej.
Derivation Procedure -
Krok 1 - Uwzględnij symbol początkowy w Y1 i zainicjuj i = 1.
Krok 2 - Uwzględnij wszystkie symbole, Yi+1, z którego można wywodzić Yi i uwzględnij wszystkie zastosowane reguły produkcji.
Krok 3 - Przyrost i i powtórz krok 2, aż Yi+1 = Yi.
Problem
Znajdź zredukowany odpowiednik gramatyki do gramatyki G, mający reguły produkcji, P: S → AC | B, A → a, C → c | BC, E → aA | mi
Rozwiązanie
Phase 1 -
T = {a, c, e}
W 1 = {A, C, E} z reguł A → a, C → c i E → aA
W 2 = {A, C, E} U {S} z reguły S → AC
W 3 = {A, C, E, S} U ∅
Ponieważ W 2 = W 3 , możemy wyprowadzić G 'jako -
G '= {{A, C, E, S}, {a, c, e}, P, {S}}
gdzie P: S → AC, A → a, C → c, E → aA | mi
Phase 2 -
Y 1 = {S}
Y 2 = {S, A, C} z reguły S → AC
Y 3 = {S, A, C, a, c} z reguł A → a i C → c
Y 4 = {S, A, C, a, c}
Ponieważ Y 3 = Y 4 , możemy wyprowadzić G ”jako -
G ”= {{A, C, S}, {a, c}, P, {S}}
gdzie P: S → AC, A → a, C → c
Usunięcie produkcji jednostkowej
Dowolna reguła produkcji w postaci A → B, gdzie A, B ∈ wywoływana jest nieterminalna unit production..
Procedura usuwania -
Step 1 - Aby usunąć A → Bdodaj produkcję A → x do reguły gramatyki kiedykolwiek B → xwystępuje w gramatyce. [x ∈ Terminal, x może mieć wartość Null]
Step 2 - Usuń A → B z gramatyki.
Step 3 - Powtarzaj od kroku 1, aż wszystkie produkcje jednostkowe zostaną usunięte.
Problem
Usuń produkcję jednostkową z następujących -
S → XY, X → a, Y → Z | b, Z → M, M → N, N → a
Solution -
W gramatyce są 3 produkcje jednostkowe -
Y → Z, Z → M i M → N
At first, we will remove M → N.
Ponieważ N → a, dodajemy M → a, a M → N jest usuwane.
Zestaw produkcyjny staje się
S → XY, X → a, Y → Z | b, Z → M, M → a, N → a
Now we will remove Z → M.
Jako M → a dodajemy Z → a, a Z → M jest usuwane.
Zestaw produkcyjny staje się
S → XY, X → a, Y → Z | b, Z → a, M → a, N → a
Now we will remove Y → Z.
Jako Z → a dodajemy Y → a, a Y → Z jest usuwane.
Zestaw produkcyjny staje się
S → XY, X → a, Y → a | b, Z → a, M → a, N → a
Teraz Z, M i N są nieosiągalne, dlatego możemy je usunąć.
Ostateczna wersja CFG jest bez produkcji jednostkowej -
S → XY, X → a, Y → a | b
Usunięcie Null Productions
W CFG: symbol nieterminalny ‘A’ jest zmienną dopuszczającą wartość null, jeśli istnieje produkcja A → ε lub istnieje wyprowadzenie, które zaczyna się od A i ostatecznie kończy się
ε: A → .......… → ε
Procedura usuwania
Step 1 - Znajdź zmienne nieterminalne dopuszczające wartość null, które wyprowadzają ε.
Step 2 - Do każdej produkcji A → a, skonstruuj wszystkie produkcje A → x gdzie x jest uzyskiwany z ‘a’ usuwając jeden lub wiele nieterminali z kroku 1.
Step 3 - Połącz oryginalne produkcje z wynikiem kroku 2 i usuń ε - productions.
Problem
Usuń zerową produkcję z następujących -
S → ASA | aB | b, A → B, B → b | ∈
Solution -
Istnieją dwie zmienne dopuszczające wartość null - A i B
At first, we will remove B → ε.
Po usunięciu B → ε, zestaw produkcyjny staje się -
S → ASA | aB | b | a, A ε B | b | & epsilon, B → b
Now we will remove A → ε.
Po usunięciu A → ε, zestaw produkcyjny staje się -
S → ASA | aB | b | a | SA | AS | S, A → B | b, B → b
To jest ostateczny zestaw produkcyjny bez przejścia zerowego.
CFG jest w normalnej formie Chomsky'ego, jeśli produkcje są w następujących formach -
- A → a
- A → BC
- S → ε
gdzie A, B i C to nieterminale i a jest terminalem.
Algorytm konwersji do postaci normalnej Chomsky'ego -
Step 1 - Jeśli symbol startu S występuje po prawej stronie, utwórz nowy symbol początku S’ i nową produkcję S’→ S.
Step 2- Usuń zerowe produkcje. (Korzystanie z omówionego wcześniej algorytmu usuwania Null Production)
Step 3- Usuń produkcje jednostkowe. (Korzystanie z omówionego wcześniej algorytmu usuwania produkcji jednostkowej)
Step 4 - Wymień każdą produkcję A → B1…Bn gdzie n > 2 z A → B1C gdzie C → B2 …Bn. Powtórz ten krok dla wszystkich produkcji, które mają dwa lub więcej symboli po prawej stronie.
Step 5 - Jeśli prawa strona jakiejkolwiek produkcji jest w formie A → aB gdzie a jest terminalem, a A, B są nieterminalne, wtedy produkcja zostaje zastąpiona przez A → XB i X → a. Powtórz ten krok dla każdej produkcji, która jest w formieA → aB.
Problem
Zamień następujący CFG na CNF
S → ASA | aB, A → B | S, B → b | ε
Rozwiązanie
(1) Od S pojawia się w RHS, dodajemy nowy stan S0 i S0→S jest dodawany do zestawu produkcyjnego i staje się -
S 0 → S, S → ASA | aB, A → B | S, B → b | ∈
(2) Teraz usuniemy zerowe produkcje -
B → ∈ i A → ∈
Po usunięciu B → ε zbiór produkcyjny staje się -
S 0 → S, S → ASA | aB | a, A → B | S | ∈, B → b
Po usunięciu A → ∈ zestaw produkcyjny staje się -
S 0 → S, S → ASA | aB | a | AS | SA | S, A → B | S, B → b
(3) Teraz usuniemy produkcje jednostkowe.
Po usunięciu S → S zestaw produkcyjny staje się -
S 0 → S, S → ASA | aB | a | AS | SA, A → B | S, B → b
Po usunięciu S 0 → S zestaw produkcyjny staje się -
S 0 → ASA | aB | a | AS | SA, S → ASA | aB | a | AS | SA
A → B | S, B → b
Po usunięciu A → B zestaw produkcyjny staje się -
S 0 → ASA | aB | a | AS | SA, S → ASA | aB | a | AS | SA
A → S | b
B → b
Po usunięciu A → S zestaw produkcyjny staje się -
S 0 → ASA | aB | a | AS | SA, S → ASA | aB | a | AS | SA
A → b | ASA | aB | a | AS | SA, B → b
(4) Teraz dowiemy się więcej niż dwóch zmiennych w RHS
Tutaj S 0 → ASA, S → ASA, A → ASA narusza dwa nie-zaciski w RHS
Dlatego zastosujemy krok 4 i krok 5, aby uzyskać następujący końcowy zestaw produkcyjny, który jest w CNF -
S 0 → AX | aB | a | AS | SA
S → AX | aB | a | AS | SA
A → b | AX | aB | a | AS | SA
B → b
X → SA
(5)Musimy zmienić produkcje S 0 → aB, S → aB, A → aB
A ostateczny zestaw produkcyjny to -
S 0 → AX | YB | a | AS | SA
S → AX | YB | a | AS | SA
A → b A → b | AX | YB | a | AS | SA
B → b
X → SA
Y → a
CFG jest w normalnej formie Greibach, jeśli produkcje są w następujących formach -
A → b
A → bD 1 … D n
S → ε
gdzie A, D 1 , ...., D n to nieterminale, a b to terminal.
Algorytm konwersji CFG do postaci normalnej Greibach
Step 1 - Jeśli symbol startu S występuje po prawej stronie, utwórz nowy symbol początku S’ i nową produkcję S’ → S.
Step 2- Usuń zerowe produkcje. (Korzystanie z omówionego wcześniej algorytmu usuwania Null Production)
Step 3- Usuń produkcje jednostkowe. (Korzystanie z omówionego wcześniej algorytmu usuwania produkcji jednostkowej)
Step 4 - Usuń całą bezpośrednią i pośrednią lewostronną rekursję.
Step 5 - Wykonuj odpowiednie podstawienia produkcji, aby zamienić je na właściwą formę GNF.
Problem
Zamień następujący CFG na CNF
S → XY | Xn | p
X → mX | m
Y → Xn | o
Rozwiązanie
Tutaj, Snie pojawia się po prawej stronie żadnej produkcji i nie ma produkcji jednostkowej lub zerowej w zestawie reguł produkcji. Możemy więc pominąć krok 1 do kroku 3.
Step 4
Teraz po wymianie
X w S → XY | Xo | p
z
mX | m
otrzymujemy
S → mXY | mY | mXo | mo | p.
A po wymianie
X w Y → X n | o
prawą stroną
X → mX | m
otrzymujemy
Y → mXn | mn | o.
Do zestawu produkcyjnego dodano dwie nowe produkcje O → o i P → p, a następnie doszliśmy do ostatecznego GNF w następujący sposób -
S → mXY | mY | mXC | mC | p
X → mX | m
Y → mXD | mD | o
O → o
P → p
Lemat
Gdyby L jest językiem bezkontekstowym, ma długość pompowania p taki, że dowolny ciąg w ∈ L długości ≥ p można zapisać jako w = uvxyz, gdzie vy ≠ ε, |vxy| ≤ pi dla wszystkich i ≥ 0, uvixyiz ∈ L.
Zastosowania lematu pompowania
Lemat o pompowaniu służy do sprawdzania, czy gramatyka jest bezkontekstowa, czy nie. Weźmy przykład i pokażmy, jak jest sprawdzany.
Problem
Dowiedz się, czy język L = {xnynzn | n ≥ 1} jest bezkontekstowa czy nie.
Rozwiązanie
Pozwolić Ljest bezkontekstowa. Następnie,L musi spełniać lemat o pompowaniu.
Najpierw wybierz liczbę nlematu o pompowaniu. Następnie przyjmij z jako 0 n 1 n 2 n .
Przerwa z w uvwxy, gdzie
|vwx| ≤ n and vx ≠ ε.
W związku z tym vwxnie może obejmować zarówno zer, jak i 2, ponieważ ostatnie 0 i pierwsze 2 są oddalone od siebie o co najmniej (n + 1). Istnieją dwa przypadki -
Case 1 - vwxnie ma 2s. Następnievxma tylko 0 i 1. Następnieuwy, który musiałby być w L, ma n 2 s, ale mniej niż n 0s lub 1s.
Case 2 - vwx nie ma zer.
Tutaj pojawia się sprzeczność.
W związku z tym, L nie jest językiem bezkontekstowym.
Podstawowa struktura PDA
Automat przesuwający to sposób na zaimplementowanie gramatyki bezkontekstowej w podobny sposób, w jaki projektujemy DFA dla zwykłej gramatyki. DFA może zapamiętać skończoną ilość informacji, ale PDA może zapamiętać nieskończoną ilość informacji.
Zasadniczo automat przesuwający to -
"Finite state machine" + "a stack"
Automat przesuwający składa się z trzech elementów -
- taśma wejściowa,
- jednostka sterująca, i
- stos o nieskończonej wielkości.
Głowica stosu skanuje górny symbol stosu.
Stos wykonuje dwie operacje -
Push - u góry zostanie dodany nowy symbol.
Pop - czyta się i usuwa górny symbol.
PDA może czytać symbol wejściowy lub nie, ale musi czytać wierzchołek stosu w każdym przejściu.
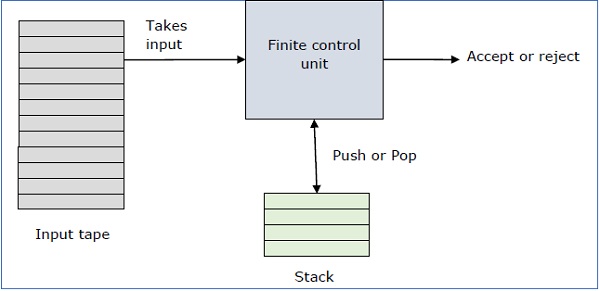
PDA można formalnie opisać jako 7-krotkę (Q, ∑, S, δ, q 0 , I, F) -
Q jest skończoną liczbą stanów
∑ jest alfabetem wejściowym
S to symbole stosu
δ jest funkcją przejścia: Q × (∑ ∪ {ε}) × S × Q × S *
q0jest stanem początkowym (q 0 ∈ Q)
I jest początkowym symbolem wierzchołka stosu (I ∈ S)
F jest zbiorem stanów akceptujących (F ∈ Q)
Poniższy diagram pokazuje przejście PDA ze stanu q 1 do stanu q 2 , oznaczone jako a, b → c -

To znaczy w stanie q1, jeśli napotkamy ciąg wejściowy ‘a’ a górnym symbolem stosu jest ‘b’, potem pop ‘b’, Pchać ‘c’ na szczycie stosu i przejdź do stanu q2.
Terminologie związane z PDA
Natychmiastowy opis
Natychmiastowy opis (ID) PDA jest reprezentowany przez trójkę (q, w, s) gdzie
q jest stan
w jest nieużywanym wejściem
s to zawartość stosu
Notacja kołowrotu
Notacja „kołowrót” jest używana do łączenia par identyfikatorów, które reprezentują jeden lub więcej ruchów PDA. Proces przejścia oznaczony jest symbolem kołowrotu „⊢”.
Rozważ PDA (Q, ∑, S, δ, q 0 , I, F). Przejście można matematycznie przedstawić za pomocą następującego zapisu kołowrotu -
(p, aw, Tβ) ⊢ (q, w, αb)Oznacza to, że podczas przechodzenia ze stanu p określić q, symbol wejścia ‘a’ jest zużyty, a wierzchołek stosu ‘T’ jest zastępowany nowym ciągiem ‘α’.
Note - Jeśli chcemy zero lub więcej ruchów PDA, musimy użyć do tego symbolu (⊢ *).
Istnieją dwa różne sposoby definiowania akceptowalności urządzeń PDA.
Dopuszczalność w stanie końcowym
W stanie końcowym akceptowalnym PDA akceptuje ciąg znaków, gdy po odczytaniu całego ciągu PDA jest w stanie końcowym. Od stanu początkowego możemy wykonywać ruchy, które kończą się stanem końcowym z dowolnymi wartościami stosu. Wartości stosu nie mają znaczenia, o ile osiągniemy stan ostateczny.
Dla PDA (Q, ∑, S, δ, q 0 , I, F) językiem akceptowanym przez zbiór stanów końcowych F jest -
L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, x), q ∈ F}
dla dowolnego ciągu stosu wejściowego x.
Dopuszczalność pustego stosu
Tutaj PDA akceptuje ciąg znaków, gdy po odczytaniu całego ciągu PDA opróżnił swój stos.
Dla PDA (Q, ∑, S, δ, q 0 , I, F) językiem akceptowanym przez pusty stos jest -
L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, ε), q ∈ Q}
Przykład
Skonstruuj PDA, który akceptuje L = {0n 1n | n ≥ 0}
Rozwiązanie

Ten język akceptuje L = {ε, 01, 0011, 000111, .............................}
Tutaj, w tym przykładzie, liczba ‘a’ i ‘b’ muszą być takie same.
Początkowo umieściliśmy specjalny symbol ‘$’ do pustego stosu.
Następnie w stanie q2, jeśli napotkamy wejście 0 i top ma wartość Null, wrzucamy 0 do stosu. To może się powtarzać. A jeśli napotkamy dane wejściowe 1 i top jest 0, to zerujemy.
Następnie w stanie q3, jeśli napotkamy wejście 1, a top jest równy 0, zdejmujemy to 0. Może to również spowodować iterację. A jeśli napotkamy dane wejściowe 1 i top jest 0, zdejmujemy górny element.
Jeśli na szczycie stosu zostanie napotkany specjalny symbol „$”, jest on wyskakiwany i ostatecznie przechodzi do stanu akceptacji q 4 .
Przykład
Skonstruuj PDA, który akceptuje L = {ww R | w = (a + b) *}
Solution

Początkowo umieszczamy specjalny symbol „$” w pustym stosie. W stanieq2, the wczyta się. Uroczyścieq3, każde 0 lub 1 jest zdejmowane, gdy pasuje do wejścia. Jeśli podane zostanie jakiekolwiek inne wejście, PDA przejdzie w stan nieaktywny. Kiedy osiągamy ten specjalny symbol „$”, przechodzimy do stanu akceptacjiq4.
Jeśli gramatyka G jest bezkontekstowy, możemy zbudować równoważny niedeterministyczny PDA, który akceptuje język, który jest tworzony przez gramatykę bezkontekstową G. Dla gramatyki można zbudować parserG.
Także jeśli P jest automatem przesuwającym w dół, można skonstruować równoważną gramatykę bezkontekstową G, gdzie
L(G) = L(P)
W następnych dwóch tematach omówimy, jak konwertować z PDA do CFG i odwrotnie.
Algorytm znajdowania PDA odpowiadającego danemu CFG
Input - A CFG, G = (V, T, P, S)
Output- Równoważne PDA, P = (Q, ∑, S, δ, q 0 , I, F)
Step 1 - Zamień produkcje CFG na GNF.
Step 2 - PDA będzie miał tylko jeden stan {q}.
Step 3 - Symbol startu CFG będzie symbolem startu w PDA.
Step 4 - Wszystkie nieterminale CFG będą symbolami stosu PDA, a wszystkie terminale CFG będą symbolami wejściowymi PDA.
Step 5 - Do każdej produkcji w formie A → aX gdzie a jest terminalem i A, X są kombinacją terminali i nieterminali, wykonaj przejście δ (q, a, A).
Problem
Skonstruuj PDA na podstawie poniższego CFG.
G = ({S, X}, {a, b}, P, S)
gdzie są produkcje -
S → XS | ε , A → aXb | Ab | ab
Rozwiązanie
Niech równoważny PDA,
P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)
gdzie δ -
δ (q, ε, S) = {(q, XS), (q, ε)}
δ (q, ε, X) = {(q, aXb), (q, Xb), (q, ab)}
δ (q, a, a) = {(q, ε)}
δ (q, 1, 1) = {(q, ε)}
Algorytm znajdowania CFG odpowiadającego danemu PDA
Input - A CFG, G = (V, T, P, S)
Output- Równoważne PDA, P = (Q, ∑, S, δ, q 0 , I, F) takie, że nieterminalami gramatyki G będą {X wx | W, X ∈ P} i stanu początkowego będzie Q0, M .
Step 1- Dla każdego w, x, y, z ∈ Q, m ∈ S i a, b ∈ ∑, jeśli δ (w, a, ε) zawiera (y, m) i (z, b, m) zawiera (x, ε), dodaj regułę produkcji X wx → a X yz b w gramatyce G.
Step 2- Dla każdego w, x, y, z ∈ Q dodaj regułę produkcji X wx → X wy X yx w gramatyce G.
Step 3- Dla w ∈ Q dodaj regułę produkcji X ww → ε w gramatyce G.
Parsowanie służy do wyprowadzenia ciągu znaków przy użyciu reguł produkcji gramatyki. Służy do sprawdzania dopuszczalności łańcucha. Kompilator służy do sprawdzania, czy łańcuch jest poprawny składniowo. Parser pobiera dane wejściowe i buduje drzewo analizy.
Parser może być dwojakiego rodzaju -
Top-Down Parser - Analiza odgórna zaczyna się od góry z symbolem startu i wyprowadza łańcuch przy użyciu drzewa parsowania.
Bottom-Up Parser - Analiza oddolna zaczyna się od dołu ciągiem i dochodzi do symbolu początkowego przy użyciu drzewa parsowania.
Projekt parsera odgórnego
W przypadku analizowania zstępującego, PDA ma następujące cztery typy przejść -
Popchnij nieterminal po lewej stronie produkcji na szczycie stosu i popchnij jego ciąg po prawej stronie.
Jeśli najwyższy symbol stosu pasuje do odczytywanego symbolu wejściowego, należy go zdjąć.
Wsuń symbol początkowy „S” do stosu.
Jeśli ciąg wejściowy jest w pełni odczytany, a stos jest pusty, przejdź do stanu końcowego „F”.
Przykład
Zaprojektuj odgórny parser dla wyrażenia "x + y * z" dla gramatyki G z następującymi regułami produkcji -
P: S → S + X | X, X → X * Y | Y, Y → (S) | ID
Solution
Jeśli PDA to (Q, ∑, S, δ, q 0 , I, F), to analiza odgórna wynosi -
(x + y * z, I) ⊢ (x + y * z, SI) ⊢ (x + y * z, S + XI) ⊢ (x + y * z, X + XI)
⊢ (x + y * z, Y + XI) ⊢ (x + y * z, x + XI) ⊢ (+ y * z, + XI) ⊢ (y * z, XI)
⊢ (y * z, X * YI) ⊢ (y * z, y * YI) ⊢ (* z, * YI) ⊢ (z, YI) ⊢ (z, zI) ⊢ (ε, I)
Projekt parsera oddolnego
W przypadku analizy oddolnej PDA ma następujące cztery typy przejść -
Wepchnij bieżący symbol wejściowy do stosu.
Zastąp prawą stronę produkcji na górze stosu lewą stroną.
Jeśli wierzchołek elementu stosu pasuje do bieżącego symbolu wejściowego, zdejmij go.
Jeśli ciąg wejściowy jest w pełni odczytany i tylko wtedy, gdy symbol początkowy „S” pozostaje na stosie, zdejmij go i przejdź do stanu końcowego „F”.
Przykład
Zaprojektuj odgórny parser dla wyrażenia "x + y * z" dla gramatyki G z następującymi regułami produkcji -
P: S → S + X | X, X → X * Y | Y, Y → (S) | ID
Solution
Jeśli PDA to (Q, ∑, S, δ, q 0 , I, F), to analiza oddolna wynosi -
(x + y * z, I) ⊢ (+ y * z, xI) ⊢ (+ y * z, YI) ⊢ (+ y * z, XI) ⊢ (+ y * z, SI)
⊢ (y * z, + SI) ⊢ (* z, y + SI) ⊢ (* z, Y + SI) ⊢ (* z, X + SI) ⊢ (z, * X + SI)
⊢ (ε, z * X + SI) ⊢ (ε, Y * X + SI) ⊢ (ε, X + SI) ⊢ (ε, SI)
Maszyna Turinga to urządzenie akceptujące, które akceptuje języki (zestaw rekurencyjnie wyliczalny) generowane przez gramatyki typu 0. Został wynaleziony w 1936 roku przez Alana Turinga.
Definicja
Maszyna Turinga (TM) to model matematyczny składający się z taśmy o nieskończonej długości, podzielonej na komórki, na których podawane są dane wejściowe. Składa się z głowicy odczytującej taśmę wejściową. Rejestr stanu przechowuje stan maszyny Turinga. Po odczytaniu symbolu wejściowego jest zastępowany innym symbolem, zmienia się jego stan wewnętrzny i przechodzi z jednej komórki w prawo lub w lewo. Jeśli TM osiągnie stan końcowy, ciąg wejściowy jest akceptowany, w przeciwnym razie odrzucany.
TM można formalnie opisać jako 7-krotkę (Q, X, ∑, δ, q 0 , B, F), gdzie -
Q jest skończonym zbiorem stanów
X to alfabet taśmy
∑ jest alfabetem wejściowym
δjest funkcją przejścia; δ: Q × X → Q × X × {Przesunięcie_ w lewo, Przesunięcie_ w prawo}.
q0 jest stanem początkowym
B jest pustym symbolem
F jest zbiorem stanów końcowych
Porównanie z poprzednim automatem
Poniższa tabela przedstawia porównanie różnic między maszyną Turinga a automatem skończonym i automatem przesuwającym.
| Maszyna | Struktura danych stosu | Deterministyczne? |
|---|---|---|
| Automat skończony | NA | tak |
| Pushdown Automaton | Last In First Out (LIFO) | Nie |
| Maszyna Turinga | Nieskończona taśma | tak |
Przykład maszyny Turinga
Maszyna Turinga M = (Q, X, ∑, δ, q 0 , B, F) z
- Q = {q 0 , q 1 , q 2 , q f }
- X = {a, b}
- ∑ = {1}
- q 0 = {q 0 }
- B = pusty symbol
- F = {q f }
δ jest podane przez -
| Symbol alfabetu taśmy | Stan obecny „q 0 ” | Stan obecny „q 1 ” | Stan obecny „q 2 ” |
|---|---|---|---|
| za | 1Rq 1 | 1Lq 0 | 1Lq f |
| b | 1Lq 2 | 1Rq 1 | 1Rq f |
Tutaj przejście 1Rq 1 oznacza, że symbol zapisu to 1, taśma przesuwa się w prawo, a następny stan to q 1 . Podobnie, przejście 1Lq 2 oznacza, że symbolem zapisu jest 1, taśma przesuwa się w lewo, a następny stan to q 2 .
Złożoność czasowa i przestrzenna maszyny Turinga
W przypadku maszyny Turinga złożoność czasowa odnosi się do miary liczby ruchów taśmy, gdy maszyna jest inicjowana dla niektórych symboli wejściowych, a złożoność przestrzeni to liczba komórek zapisanych na taśmie.
Złożoność czasowa wszystkie rozsądne funkcje -
T(n) = O(n log n)
Złożoność przestrzeni TM -
S(n) = O(n)
Baza TM akceptuje język, jeśli wejdzie w stan końcowy dla dowolnego ciągu wejściowego w. Język jest rekurencyjnie wyliczalny (generowany przez gramatykę typu 0), jeśli jest akceptowany przez maszynę Turinga.
TM decyduje o języku, jeśli go akceptuje, i przechodzi w stan odrzucenia dla każdego wejścia spoza tego języka. Język jest rekurencyjny, jeśli zdecyduje o nim maszyna Turinga.
W niektórych przypadkach może się zdarzyć, że baza TM się nie zatrzyma. Taka TM akceptuje język, ale o tym nie decyduje.
Projektowanie maszyny Turinga
Podstawowe wskazówki dotyczące projektowania maszyny Turinga zostały wyjaśnione poniżej na kilku przykładach.
Przykład 1
Zaprojektuj TM tak, aby rozpoznawała wszystkie ciągi składające się z nieparzystej liczby α.
Solution
Maszyna Turinga M można zbudować za pomocą następujących ruchów -
Pozwolić q1 być stanem początkowym.
Gdyby M jest w q1; przy skanowaniu α wchodzi w stanq2 i pisze B (pusty).
Gdyby M jest w q2; przy skanowaniu α wchodzi w stanq1 i pisze B (pusty).
Z powyższych ruchów możemy to zobaczyć M wchodzi do stanu q1 jeśli skanuje parzystą liczbę α i wchodzi w stan q2jeśli skanuje nieparzystą liczbę α. W związku z tymq2 jest jedynym stanem akceptującym.
W związku z tym,
M = {{q 1 , q 2 }, {1}, {1, B}, δ, q 1 , B, {q 2 }}
gdzie δ jest podane przez -
| Symbol alfabetu taśmy | Stan obecny „q 1 ” | Stan obecny „q 2 ” |
|---|---|---|
| α | BRq 2 | BRq 1 |
Przykład 2
Zaprojektuj maszynę Turinga, która czyta łańcuch reprezentujący liczbę binarną i usuwa wszystkie wiodące zera w ciągu. Jeśli jednak ciąg składa się tylko z zer, zachowuje jedno 0.
Solution
Załóżmy, że ciąg wejściowy jest zakończony pustym symbolem B na każdym końcu łańcucha.
Maszyna Turinga, M, można zbudować za pomocą następujących ruchów -
Pozwolić q0 być stanem początkowym.
Gdyby M jest w q0po odczytaniu 0 przesuwa się w prawo, wchodzi w stan q1 i usuwa 0. Przy odczycie 1 wchodzi w stan q2 i porusza się w prawo.
Gdyby M jest w q1, po odczytaniu 0, przesuwa się w prawo i kasuje 0, tj. zastępuje 0 przez B. Po osiągnięciu skrajnej lewej cyfry 1, wchodziq2i porusza się w prawo. Jeśli osiągnie B, czyli ciąg składa się tylko z zer, przesuwa się w lewo i wchodzi w stanq3.
Gdyby M jest w q2po odczytaniu 0 lub 1 przesuwa się w prawo. Po osiągnięciu B przesuwa się w lewo i wchodzi w stanq4. To potwierdza, że ciąg składa się tylko z 0 i 1.
Gdyby M jest w q3, zastępuje B przez 0, przesuwa się w lewo i osiąga stan końcowy qf.
Gdyby M jest w q4po odczytaniu 0 lub 1 przesuwa się w lewo. Po osiągnięciu początku łańcucha, tj. Gdy odczytuje B, osiąga stan końcowyqf.
W związku z tym,
M = {{q 0 , q 1 , q 2 , q 3 , q 4 , q f }, {0,1, B}, {1, B}, δ, q 0 , B, {q f }}
gdzie δ jest podane przez -
| Symbol alfabetu taśmy | Stan obecny „q 0 ” | Stan obecny „q 1 ” | Stan obecny „q 2 ” | Stan obecny „q 3 ” | Stan obecny „q 4 ” |
|---|---|---|---|---|---|
| 0 | BRq 1 | BRq 1 | ORq 2 | - | OLq 4 |
| 1 | 1Rq2 | 1Rq2 | 1Rq2 | - | 1Lq4 |
| B | BRq1 | BLq3 | BLq4 | OLqf | BRqf |
Multi-tape Turing Machines have multiple tapes where each tape is accessed with a separate head. Each head can move independently of the other heads. Initially the input is on tape 1 and others are blank. At first, the first tape is occupied by the input and the other tapes are kept blank. Next, the machine reads consecutive symbols under its heads and the TM prints a symbol on each tape and moves its heads.

A Multi-tape Turing machine can be formally described as a 6-tuple (Q, X, B, δ, q0, F) where −
Q is a finite set of states
X is the tape alphabet
B is the blank symbol
δ is a relation on states and symbols where
δ: Q × Xk → Q × (X × {Left_shift, Right_shift, No_shift })k
where there is k number of tapes
q0 is the initial state
F is the set of final states
Note − Every Multi-tape Turing machine has an equivalent single-tape Turing machine.
Multi-track Turing machines, a specific type of Multi-tape Turing machine, contain multiple tracks but just one tape head reads and writes on all tracks. Here, a single tape head reads n symbols from n tracks at one step. It accepts recursively enumerable languages like a normal single-track single-tape Turing Machine accepts.
A Multi-track Turing machine can be formally described as a 6-tuple (Q, X, ∑, δ, q0, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a relation on states and symbols where
δ(Qi, [a1, a2, a3,....]) = (Qj, [b1, b2, b3,....], Left_shift or Right_shift)
q0 is the initial state
F is the set of final states
Note − For every single-track Turing Machine S, there is an equivalent multi-track Turing Machine M such that L(S) = L(M).
In a Non-Deterministic Turing Machine, for every state and symbol, there are a group of actions the TM can have. So, here the transitions are not deterministic. The computation of a non-deterministic Turing Machine is a tree of configurations that can be reached from the start configuration.
An input is accepted if there is at least one node of the tree which is an accept configuration, otherwise it is not accepted. If all branches of the computational tree halt on all inputs, the non-deterministic Turing Machine is called a Decider and if for some input, all branches are rejected, the input is also rejected.
A non-deterministic Turing machine can be formally defined as a 6-tuple (Q, X, ∑, δ, q0, B, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a transition function;
δ : Q × X → P(Q × X × {Left_shift, Right_shift}).
q0 is the initial state
B is the blank symbol
F is the set of final states
A Turing Machine with a semi-infinite tape has a left end but no right end. The left end is limited with an end marker.

It is a two-track tape −
Upper track − It represents the cells to the right of the initial head position.
Lower track − It represents the cells to the left of the initial head position in reverse order.
The infinite length input string is initially written on the tape in contiguous tape cells.
The machine starts from the initial state q0 and the head scans from the left end marker ‘End’. In each step, it reads the symbol on the tape under its head. It writes a new symbol on that tape cell and then it moves the head either into left or right one tape cell. A transition function determines the actions to be taken.
It has two special states called accept state and reject state. If at any point of time it enters into the accepted state, the input is accepted and if it enters into the reject state, the input is rejected by the TM. In some cases, it continues to run infinitely without being accepted or rejected for some certain input symbols.
Note − Turing machines with semi-infinite tape are equivalent to standard Turing machines.
A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some bounded finite length.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The computation is restricted to the constant bounded area. The input alphabet contains two special symbols which serve as left end markers and right end markers which mean the transitions neither move to the left of the left end marker nor to the right of the right end marker of the tape.
A linear bounded automaton can be defined as an 8-tuple (Q, X, ∑, q0, ML, MR, δ, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
q0 is the initial state
ML is the left end marker
MR is the right end marker where MR ≠ ML
δ is a transition function which maps each pair (state, tape symbol) to (state, tape symbol, Constant ‘c’) where c can be 0 or +1 or -1
F is the set of final states

A deterministic linear bounded automaton is always context-sensitive and the linear bounded automaton with empty language is undecidable..
A language is called Decidable or Recursive if there is a Turing machine which accepts and halts on every input string w. Every decidable language is Turing-Acceptable.

A decision problem P is decidable if the language L of all yes instances to P is decidable.
For a decidable language, for each input string, the TM halts either at the accept or the reject state as depicted in the following diagram −

Example 1
Find out whether the following problem is decidable or not −
Is a number ‘m’ prime?
Solution
Prime numbers = {2, 3, 5, 7, 11, 13, …………..}
Divide the number ‘m’ by all the numbers between ‘2’ and ‘√m’ starting from ‘2’.
If any of these numbers produce a remainder zero, then it goes to the “Rejected state”, otherwise it goes to the “Accepted state”. So, here the answer could be made by ‘Yes’ or ‘No’.
Hence, it is a decidable problem.
Example 2
Given a regular language L and string w, how can we check if w ∈ L?
Solution
Take the DFA that accepts L and check if w is accepted

Some more decidable problems are −
- Does DFA accept the empty language?
- Is L1 ∩ L2 = ∅ for regular sets?
Note −
If a language L is decidable, then its complement L' is also decidable
If a language is decidable, then there is an enumerator for it.
For an undecidable language, there is no Turing Machine which accepts the language and makes a decision for every input string w (TM can make decision for some input string though). A decision problem P is called “undecidable” if the language L of all yes instances to P is not decidable. Undecidable languages are not recursive languages, but sometimes, they may be recursively enumerable languages.

Example
- The halting problem of Turing machine
- The mortality problem
- The mortal matrix problem
- The Post correspondence problem, etc.
Input − A Turing machine and an input string w.
Problem − Does the Turing machine finish computing of the string w in a finite number of steps? The answer must be either yes or no.
Proof − At first, we will assume that such a Turing machine exists to solve this problem and then we will show it is contradicting itself. We will call this Turing machine as a Halting machine that produces a ‘yes’ or ‘no’ in a finite amount of time. If the halting machine finishes in a finite amount of time, the output comes as ‘yes’, otherwise as ‘no’. The following is the block diagram of a Halting machine −

Now we will design an inverted halting machine (HM)’ as −
If H returns YES, then loop forever.
If H returns NO, then halt.
The following is the block diagram of an ‘Inverted halting machine’ −

Further, a machine (HM)2 which input itself is constructed as follows −
- If (HM)2 halts on input, loop forever.
- Else, halt.
Here, we have got a contradiction. Hence, the halting problem is undecidable.
Rice theorem states that any non-trivial semantic property of a language which is recognized by a Turing machine is undecidable. A property, P, is the language of all Turing machines that satisfy that property.
Formal Definition
If P is a non-trivial property, and the language holding the property, Lp , is recognized by Turing machine M, then Lp = {<M> | L(M) ∈ P} is undecidable.
Description and Properties
Property of languages, P, is simply a set of languages. If any language belongs to P (L ∈ P), it is said that L satisfies the property P.
A property is called to be trivial if either it is not satisfied by any recursively enumerable languages, or if it is satisfied by all recursively enumerable languages.
A non-trivial property is satisfied by some recursively enumerable languages and are not satisfied by others. Formally speaking, in a non-trivial property, where L ∈ P, both the following properties hold:
Property 1 − There exists Turing Machines, M1 and M2 that recognize the same language, i.e. either ( <M1>, <M2> ∈ L ) or ( <M1>,<M2> ∉ L )
Property 2 − There exists Turing Machines M1 and M2, where M1 recognizes the language while M2 does not, i.e. <M1> ∈ L and <M2> ∉ L
Proof
Suppose, a property P is non-trivial and φ ∈ P.
Since, P is non-trivial, at least one language satisfies P, i.e., L(M0) ∈ P , ∋ Turing Machine M0.
Let, w be an input in a particular instant and N is a Turing Machine which follows −
On input x
- Run M on w
- If M does not accept (or doesn't halt), then do not accept x (or do not halt)
- If M accepts w then run M0 on x. If M0 accepts x, then accept x.
A function that maps an instance ATM = {<M,w>| M accepts input w} to a N such that
- If M accepts w and N accepts the same language as M0, Then L(M) = L(M0) ∈ p
- If M does not accept w and N accepts φ, Then L(N) = φ ∉ p
Since ATM is undecidable and it can be reduced to Lp, Lp is also undecidable.
The Post Correspondence Problem (PCP), introduced by Emil Post in 1946, is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x1, x2, x3,………, xn)
N = (y1, y2, y3,………, yn)
We can say that there is a Post Correspondence Solution, if for some i1,i2,………… ik, where 1 ≤ ij ≤ n, the condition xi1 …….xik = yi1 …….yik satisfies.
Example 1
Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
have a Post Correspondence Solution?
Solution
| x1 | x2 | x3 | |
|---|---|---|---|
| M | Abb | aa | aaa |
| N | Bba | aaa | aa |
Here,
x2x1x3 = ‘aaabbaaa’
and y2y1y3 = ‘aaabbaaa’
We can see that
x2x1x3 = y2y1y3
Hence, the solution is i = 2, j = 1, and k = 3.
Example 2
Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post Correspondence Solution?
Solution
| x1 | x2 | x3 | |
|---|---|---|---|
| M | ab | bab | bbaaa |
| N | a | ba | bab |
In this case, there is no solution because −
| x2x1x3 | ≠ | y2y1y3 | (Lengths are not same)
Hence, it can be said that this Post Correspondence Problem is undecidable.