Niedeterministyczny automat skończony
W NDFA, dla określonego symbolu wejściowego, maszyna może przejść do dowolnej kombinacji stanów w maszynie. Innymi słowy, nie można określić dokładnego stanu, do którego porusza się maszyna. Stąd to się nazywaNon-deterministic Automaton. Ponieważ ma skończoną liczbę stanów, nazywana jest maszynąNon-deterministic Finite Machine lub Non-deterministic Finite Automaton.
Formalna definicja NDFA
NDFA można przedstawić jako 5-krotkę (Q, ∑, δ, q 0 , F), gdzie -
Q jest skończonym zbiorem stanów.
∑ jest skończonym zbiorem symboli zwanych alfabetami.
δjest funkcją przejścia, gdzie δ: Q × ∑ → 2 Q
(Tutaj pobrano zestaw mocy Q (2 Q ), ponieważ w przypadku NDFA ze stanu może nastąpić przejście do dowolnej kombinacji stanów Q)
q0jest stanem początkowym, z którego przetwarzane jest dowolne wejście (q 0 ∈ Q).
F jest zbiorem stanu / stanów końcowych Q (F ⊆ Q).
Graficzna reprezentacja NDFA: (tak samo jak DFA)
NDFA jest reprezentowane przez digrafy zwane diagramem stanów.
- Wierzchołki reprezentują stany.
- Łuki oznaczone alfabetem wejściowym pokazują przejścia.
- Stan początkowy jest oznaczony pustym pojedynczym łukiem wejściowym.
- Stan końcowy jest oznaczony podwójnymi kółkami.
Example
Niech niedeterministyczny automat skończony będzie →
- Q = {a, b, c}
- ∑ = {0, 1}
- q 0 = {a}
- F = {c}
Funkcja przejścia δ, jak pokazano poniżej -
| Stan obecny | Następny stan dla wejścia 0 | Następny stan dla wejścia 1 |
|---|---|---|
| za | a, b | b |
| b | do | a, c |
| do | pne | do |
Jej reprezentacja graficzna wyglądałaby następująco -
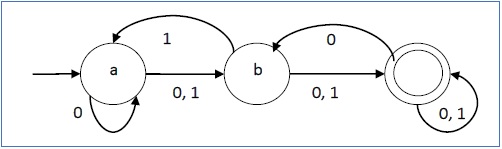
DFA vs NDFA
W poniższej tabeli wymieniono różnice między usługami DFA i NDFA.
| DFA | NDFA |
|---|---|
| Przejście ze stanu następuje do jednego określonego następnego stanu dla każdego symbolu wejściowego. Dlatego nazywa się to deterministycznym . | Przejście ze stanu może następować do wielu następnych stanów dla każdego symbolu wejściowego. Dlatego nazywa się to niedeterministycznym . |
| Puste przejścia ciągów nie są widoczne w DFA. | NDFA zezwala na przejścia pustych ciągów. |
| Wycofywanie jest dozwolone w DFA | W NDFA cofanie się nie zawsze jest możliwe. |
| Wymaga więcej miejsca. | Zajmuje mniej miejsca. |
| Ciąg jest akceptowany przez DFA, jeśli przechodzi do stanu końcowego. | Ciąg jest akceptowany przez NDFA, jeśli przynajmniej jedno ze wszystkich możliwych przejść kończy się w stanie końcowym. |
Akceptory, klasyfikatory i przetworniki
Akceptor (rozpoznający)
Automat obliczający funkcję boolowską nazywa się acceptor. Wszystkie stany akceptora albo akceptują, albo odrzucają dane mu wejściowe.
Klasyfikator
ZA classifier ma więcej niż dwa stany końcowe i daje jedno wyjście po zakończeniu.
Transduktor
Automat, który generuje dane wyjściowe na podstawie bieżącego wejścia i / lub poprzedniego stanu, nazywany jest a transducer. Przetworniki mogą być dwojakiego rodzaju -
Mealy Machine - Wyjście zależy zarówno od aktualnego stanu, jak i aktualnego wejścia.
Moore Machine - Wyjście zależy tylko od aktualnego stanu.
Dopuszczalność przez DFA i NDFA
Ciąg jest akceptowany przez DFA / NDFA, jeśli DFA / NDFA rozpoczynający się w stanie początkowym kończy się stanem akceptacji (dowolnym ze stanów końcowych) po całkowitym przeczytaniu ciągu.
Ciąg S jest akceptowany przez DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S) ∈ F
Język L akceptowane przez DFA / NDFA
{S | S ∈ ∑* and δ*(q0, S) ∈ F}
Ciąg S ′ nie jest akceptowany przez DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S′) ∉ F
Językiem L 'nieakceptowanym przez DFA / NDFA (Uzupełnienie akceptowanego języka L) jest
{S | S ∈ ∑* and δ*(q0, S) ∉ F}
Example
Rozważmy DFA pokazane na rysunku 1.3. Z DFA można wyprowadzić dopuszczalne ciągi.

Ciągi akceptowane przez powyższy DFA: {0, 00, 11, 010, 101, ...........}
Ciągi nieakceptowane przez powyższy DFA: {1, 011, 111, ........}