Wykreślanie liczb wymiernych na osi liczbowej

Definicja

Liczba wymierna jest ułamkiem i jest wykreślana na osi liczbowej w następujący sposób.

Basic rules of representing rational no. on number line

Jeśli liczba wymierna (ułamek) jest właściwa, to mieści się między 0 a 1.
Jeśli numer wymierny (ułamek) jest niewłaściwy, to najpierw zamieniamy go na ułamek mieszany, a następnie podany numer wymierny. leży między liczbą całkowitą a następną liczbą całkowitą.

Wykonujemy następujące kroki, aby przedstawić liczbę wymierną lub ułamek, na przykład $ \ frac {5} {7} $ na osi liczbowej.

Step 1 - Rysujemy oś liczbową.

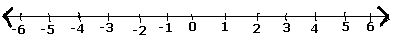
Step 2- Ponieważ liczba $ \ frac {5} {7} $ jest liczbą dodatnią, leży po prawej stronie zera.

Step 3- Tak więc po znaku zerowym mamy $ \ frac {1} {7}, \: \ frac {2} {7}, \: \ frac {3} {7}, \: \ frac {4} {7 }, \: \ frac {5} {7}, \: \ frac {6} {7}, $ i ( $ \ frac {7} {7} $ = 1).

Step 4- Liczba wymierna $ \ frac {5} {7} $ na osi liczbowej jest pokazana w następujący sposób.

Przykład 1:

Wykreśl $ \ frac {1} {4} $ i $ 1 \ frac {2} {4} $ na osi liczbowej poniżej

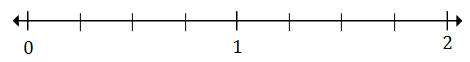
Rozwiązanie

Step 1:

$ \ frac {1} {4} $ (A) leży między 0 a 1; $ 1 \ frac {2} {4} $ (B) mieści się między 1 a 2

Step 2:

Każdy podział jest podzielony na cztery części, ponieważ dolna część ułamków wynosi 4.

$ \ frac {1} {4} $ to pierwszy znak po 0, dlatego punkt A reprezentuje $ \ frac {1} {4} $

$ 1 \ frac {2} {4} $ to drugi znak po 1, więc punkt B reprezentuje $ 1 \ frac {2} {4} $

Przykład 2:

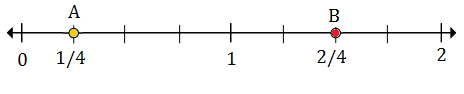
Wykreśl $ \ frac {5} {8} $ i $ 2 \ frac {3} {8} $ na osi liczbowej poniżej

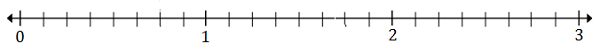
Rozwiązanie

Step 1:

$ \ frac {5} {8} $ 8 (A) leży między 0 a 1; $ 2 \ frac {3} {8} $ (B) leży między 2 a 3

Step 2:

Każdy podział jest podzielony na osiem części, ponieważ dolna część ułamków wynosi 8.

$ \ frac {5} {8} $ to piąty znak po 0, dlatego punkt A reprezentuje $ \ frac {5} {8} $

$ 2 \ frac {3} {8} $ to trzeci znak po 2, więc punkt B reprezentuje $ 2 \ frac {3} {8} $