Modulacja amplitudy

Wśród rodzajów technik modulacji główną klasyfikacją jest modulacja ciągłej fali i modulacja impulsowa. Techniki modulacji fali ciągłej są dalej podzielone naAmplitude Modulation i Angle Modulation.

Fala ciągła trwa w sposób ciągły bez przerw i jest to sygnał wiadomości pasma podstawowego, który zawiera informacje. Fala ta musi być modulowana.

Zgodnie ze standardową definicją: „Amplituda sygnału nośnego zmienia się zgodnie z chwilową amplitudą sygnału modulującego”. Co oznacza, że amplituda sygnału nośnego, który nie zawiera informacji, zmienia się zgodnie z amplitudą sygnału, który zawiera informacje, w każdej chwili. Można to dobrze wyjaśnić na poniższych rysunkach.

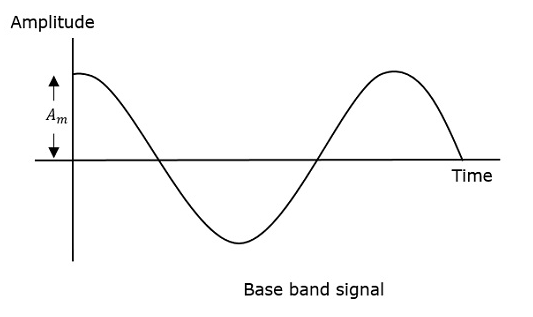
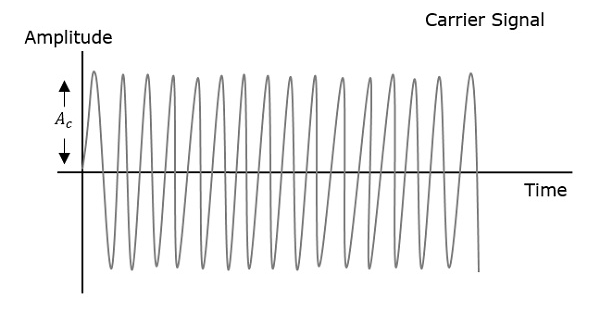
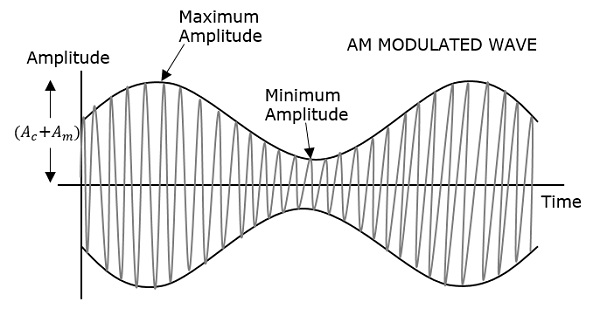
Fala modulująca, która jest pokazana jako pierwsza, jest sygnałem wiadomości. Następna to fala nośna, która jest po prostu sygnałem o wysokiej częstotliwości i nie zawiera żadnych informacji. Podczas gdy ostatnia jest wypadkową modulowaną falą.

Można zauważyć, że dodatnie i ujemne szczyty fali nośnej są połączone wyimaginowaną linią. Ta linia pomaga odtworzyć dokładny kształt sygnału modulującego. Ta wyimaginowana linia na fali nośnej nosi nazwęEnvelope. To jest to samo, co sygnał wiadomości.

Wyrażenie matematyczne

Poniżej znajduje się matematyczne wyrażenie dla tych fal.

Reprezentacja fal w dziedzinie czasu

Niech sygnał modulujący będzie -

$$ m (t) = A_mcos (2 \ pi f_mt) $$

Niech sygnał nośny będzie -

$$ c (t) = A_ccos (2 \ pi f_ct) $$

Gdzie A_m = maksymalna amplituda sygnału modulującego

A_c = maksymalna amplituda sygnału nośnego

Standardowa postać fali z modulacją amplitudy jest zdefiniowana jako -

$$ S (t) = A_c [1 + K_am (t)] cos (2 \ pi f_ct) $$

$$ S (t) = A_c [1+ \ mu cos (2 \ pi f_mt)] cos (2 \ pi f_ct) $$

$$ Gdzie, \ mu = K_aA_m $$

Indeks modulacji

Fala nośna po zmodulowaniu, jeśli wyliczany jest poziom zmodulowany, wówczas taka próba nosi nazwę Modulation Index lub Modulation Depth. Określa poziom modulacji, któremu podlega fala nośna.

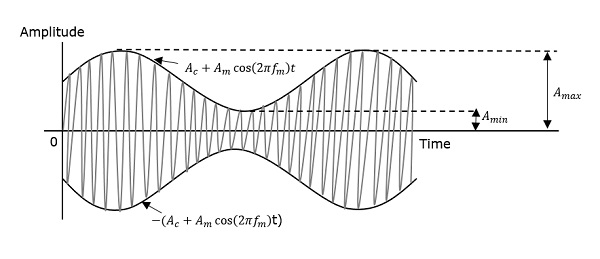
Maksymalne i minimalne wartości obwiedni modulowanej fali są reprezentowane odpowiednio przez A _max i A _min .

Spróbujmy opracować równanie dla wskaźnika modulacji.

$$ A_ {max} = A_c (1+ \ mu) $$

Ponieważ przy A _max wartość cos θ wynosi 1

$$ A_ {min} = A_c (1- \ mu) $$

Ponieważ przy A _min wartość cos θ wynosi -1

$$ \ frac {A_ {max}} {A_ {min}} = \ frac {1+ \ mu} {1- \ mu} $$

$$ A_ {max} - \ mu A_ {max} = A_ {min} + \ mu A_ {min} $$

$$ - \ mu (A_ {max} + A_ {min}) = A_ {min} -A_ {max} $$

$$ \ mu = \ frac {A_ {max} -A_ {min}} {A_ {max} + A_ {min}} $$

W ten sposób otrzymujemy równanie na współczynnik modulacji. µoznacza indeks modulacji lub głębokość modulacji. Jest to często określane w procentach zwanych jakoPercentage Modulation. Jest to zakres modulacji wyrażony w procentach i oznaczony przezm.

Aby uzyskać idealną modulację, wartość wskaźnika modulacji powinna wynosić 1, co oznacza, że głębokość modulacji powinna wynosić 100%.

Na przykład, jeśli ta wartość jest mniejsza niż 1, tj. Wskaźnik modulacji wynosi 0,5, wówczas modulowane wyjście będzie wyglądać jak na poniższym rysunku. Nazywa się to niedomodulacją. Taka fala nazywana jestunder-modulated wave.

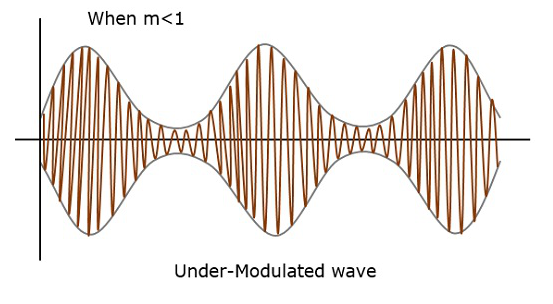
Jeśli wartość wskaźnika modulacji jest większa niż 1, tj. 1,5 lub więcej, wówczas fala będzie miała wartość over-modulated wave. Wyglądałoby to tak, jak na poniższym rysunku.

Wraz ze wzrostem wartości wskaźnika modulacji, nośna doświadcza odwrócenia fazy o 180 °, co powoduje dodatkowe wstęgi boczne, a tym samym zniekształcenie fali. Taka przemodulowana fala powoduje zakłócenia, których nie można wyeliminować.