Komunikacja satelitarna - mechanika orbitalna

Wiemy, że ścieżka satelity krążącego wokół Ziemi jest znana jako orbit. Ścieżkę tę można przedstawić za pomocą notacji matematycznych. Mechanika orbitalna to badanie ruchu satelitów obecnych na orbitach. Dzięki wiedzy o ruchu orbitalnym możemy łatwo zrozumieć operacje kosmiczne.

Elementy orbitalne

Elementy orbitalne to parametry, które są pomocne przy opisywaniu ruchu orbitalnego satelitów. Poniżej znajdują sięorbital elements.

• Półoś wielka
• Eccentricity
• Średnia anomalia
• Argument perygeum
• Inclination
• Rektascensja węzła wstępującego

Powyższe sześć elementów orbitalnych określa orbitę satelitów Ziemi. Dlatego łatwo jest odróżnić jednego satelitę od innych satelitów na podstawie wartości elementów orbitalnych.

Półoś wielka

Długość Semi-major axis (a)określa rozmiar orbity satelity. Jest to połowa większej osi. Biegnie od środka przez ognisko do krawędzi elipsy. Jest to więc promień orbity w dwóch najbardziej odległych punktach orbity.

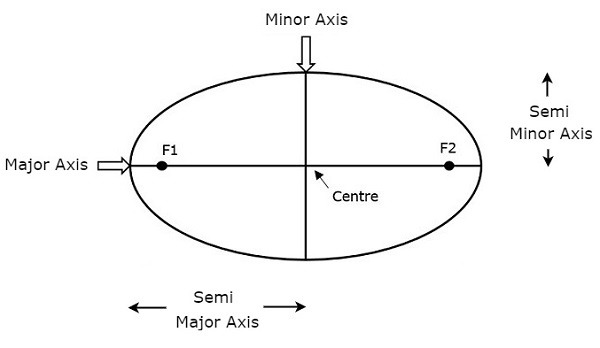
Na powyższym rysunku przedstawiono zarówno półoś dużą, jak i półoś małą. Długość półmajor axis (a) decyduje nie tylko o wielkości orbity satelity, ale także o okresie rewolucji.

Jeśli orbita kołowa jest uważana za przypadek specjalny, wówczas długość półosi wielkiej będzie równa radius tej okrągłej orbity.

Ekscentryczność

Wartość Eccentricity (e)ustala kształt orbity satelity. Ten parametr wskazuje odchylenie kształtu orbity od idealnego koła.

Jeśli długości półosi wielkiej i półosi małej eliptycznej orbity są a & b, to wyrażenie matematyczne dla eccentricity (e) będzie

$$ e = \ frac {\ sqrt {a ^ 2 - b ^ 2}} {a} $$

Wartość mimośrodu orbity kołowej wynosi zero, ponieważ oba a i b są równe. Natomiast wartość mimośrodu orbity eliptycznej mieści się w przedziale od zera do jedynki.

Następujące figure pokazuje różne orbity satelitów dla różnych wartości mimośrodowości (e)

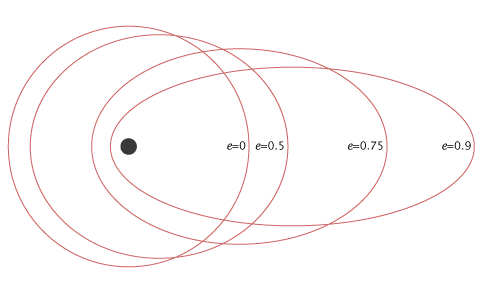
Na powyższym rysunku orbita satelity odpowiadająca zerowej wartości mimośrodowości (e) jest orbitą kołową. Pozostałe trzy orbity satelitów są eliptyczne, co odpowiada wartościom mimośrodu (e) 0,5, 0,75 i 0,9.

Średnia anomalia

W przypadku satelity punkt znajdujący się najbliżej Ziemi nazywany jest Perygeum. Mean anomaly (M) podaje średnią wartość położenia kątowego satelity w odniesieniu do perygeum.

Jeśli orbita jest kołowa, anomalia Średnia podaje kątowe położenie satelity na orbicie. Ale jeśli orbita jest eliptyczna, obliczenie dokładnej pozycji jest bardzo trudne. W tym czasie anomalia średnia jest używana jako krok pośredni.

Argument z Perygeum

Orbita satelity przecina płaszczyznę równikową w dwóch punktach. Pierwszy punkt nazywa się jakodescending node, gdzie satelita przechodzi z półkuli północnej na półkulę południową. Drugi punkt nazywa się jakoascending node, gdzie satelita przechodzi z półkuli południowej na półkulę północną.

Argument of perigee (ω)jest kątem między węzłem wstępującym a perygeum. Jeśli zarówno perygeum, jak i węzeł wstępujący istnieją w tym samym punkcie, argument perygeum będzie wynosił zero stopni

Argument perygeum jest mierzony w płaszczyźnie orbity w centrum Ziemi w kierunku ruchu satelity.

Nachylenie

Kąt między płaszczyzną orbity a płaszczyzną równikową Ziemi jest znany jako inclination (i). Jest mierzona w węźle wstępującym, z kierunkiem ze wschodu na północ. Zatem nachylenie określa orientację orbity, biorąc pod uwagę równik Ziemi jako odniesienie.

Istnieją cztery rodzaje orbit w zależności od kąta nachylenia.

• Equatorial orbit - Kąt nachylenia wynosi zero stopni lub 180 stopni.

• Polar orbit - Kąt nachylenia wynosi 90 stopni.

• Prograde orbit - Kąt nachylenia wynosi od zera do 90 stopni.

• Retrograde orbit - Kąt nachylenia wynosi od 90 do 180 stopni.

Rektascensja węzła wstępującego

Wiemy to ascending node to punkt, w którym satelita przecina płaszczyznę równikową, przechodząc z półkuli południowej na półkulę północną.

Rektascensja węzła wstępującego (Ω)to kąt między linią Barana a węzłem wstępującym w kierunku wschodnim w płaszczyźnie równikowej. Baran jest również nazywany wiosennym i równonocy.

Satelity ground trackto ścieżka na powierzchni Ziemi, która leży dokładnie poniżej jej orbity. Ścieżka naziemna satelity może przybierać różne formy w zależności od wartości elementów orbitalnych.

Równania orbitalne

W tej części omówimy równania związane z ruchem orbity.

Siły działające na satelicie

Satelita obracający się wokół Ziemi podlega działaniu siły grawitacyjnej Ziemi. Ta siła jest znana jakoCentripetal force(F ₁ ), ponieważ ta siła kieruje satelitę w jego kierunku.

Matematycznie Centripetal force(F ₁ ) działające na satelitę z powodu Ziemi można zapisać jako

$$ F_ {1} = \ frac {GMm} {R ^ 2} $$

Gdzie,

• Guniwersalna stała grawitacyjna i jest równa 6.673 X 10 ^-11 N ∙ m ² / kg ² .

• Mjest masą ziemi i jest równa 5,98 x 10 ²⁴ Kg.

• m to masa satelity.

• R to odległość od satelity do środka Ziemi.

Satelita obracający się wokół Ziemi poddawany jest działaniu siły przyciągania słońca i księżyca z powodu ich sił grawitacyjnych. Ta siła jest znana jakoCentrifugal force(F ₂ ), ponieważ ta siła odciąga satelitę od Ziemi.

Matematycznie Centrifugal force(F ₂ ) działające na satelicie można zapisać jako

$$ F_ {2} = \ frac {mv ^ 2} {R} $$

Gdzie, v jest prędkością orbitalną satelity.

Prędkość orbitalna

Prędkość orbitalna satelity to prędkość, z jaką satelita obraca się wokół Ziemi. Satelita nie odchyla się od swojej orbity i porusza się z określoną prędkością na tej orbicie, gdy zarówno siły odśrodkowe, jak i odśrodkowe sąbalance wzajemnie.

Więc, equateSiła dośrodkowa (F ₁ ) i siła odśrodkowa (F ₂ ).

$$ \ frac {GMm} {R ^ 2} = \ frac {mv ^ 2} {R} $$

$$ => \ frac {GM} {R} = v ^ 2 $$

$$ => v = \ sqrt {\ frac {GM} {R}} $$

Dlatego też orbital velocity satelity jest

$$ v = \ sqrt {\ frac {GM} {R}} $$

Gdzie,

• Gjest stałą grawitacji i jest równa 6.673 X 10 ^-11 N ∙ m ² / kg ² .

• Mjest masą ziemi i jest równa 5,98 x 10 ²⁴ Kg.

• R to odległość od satelity do środka Ziemi.

A więc głównie prędkość orbity depends na odległość od satelity do środka Ziemi (R), ponieważ G i M są stałymi.