Teoria dos autômatos - Guia rápido
Autômatos - O que é?
O termo "autômato" é derivado da palavra grega "αὐτόματα", que significa "ação automática". Um autômato (autômatos no plural) é um dispositivo de computação autopropelido abstrato que segue uma sequência predeterminada de operações automaticamente.
Um autômato com um número finito de estados é chamado de Finite Automaton (FA) ou Finite State Machine (FSM).
Definição formal de um autômato finito
Um autômato pode ser representado por uma 5-tupla (Q, ∑, δ, q 0 , F), onde -
Q é um conjunto finito de estados.
∑ é um conjunto finito de símbolos, chamado de alphabet do autômato.
δ é a função de transição.
q0é o estado inicial de onde qualquer entrada é processada (q 0 ∈ Q).
F é um conjunto de estados / estados finais de Q (F ⊆ Q).
Terminologias Relacionadas
Alfabeto
Definition - um alphabet é qualquer conjunto finito de símbolos.
Example - ∑ = {a, b, c, d} é um alphabet set onde 'a', 'b', 'c' e 'd' são symbols.
Corda
Definition - A string é uma sequência finita de símbolos tirada de ∑.
Example - 'cabcad' é uma string válida no conjunto de alfabeto ∑ = {a, b, c, d}
Comprimento de uma corda
Definition- É o número de símbolos presentes em uma string. (Denotado por|S|)
Examples -
Se S = 'cabcad', | S | = 6
Se | S | = 0, é chamado de empty string (Denotado por λ ou ε)
Kleene Star
Definition - A estrela Kleene, ∑*, é um operador unário em um conjunto de símbolos ou strings, ∑, que dá o conjunto infinito de todas as cordas possíveis de todos os comprimentos possíveis ao longo ∑ Incluindo λ.
Representation- ∑ * = ∑ 0 ∪ ∑ 1 ∪ ∑ 2 ∪ ……. onde ∑ p é o conjunto de todas as strings possíveis de comprimento p.
Example - Se ∑ = {a, b}, ∑ * = {λ, a, b, aa, ab, ba, bb, ……… ..}
Kleene Closure / Plus
Definition - o conjunto ∑+ é o conjunto infinito de todas as cordas possíveis de todos os comprimentos possíveis sobre ∑ excluindo λ.
Representation- ∑ + = ∑ 1 ∪ ∑ 2 ∪ ∑ 3 ∪ …….
∑ + = ∑ * - {λ}
Example- Se ∑ = {a, b}, ∑ + = {a, b, aa, ab, ba, bb, ……… ..}
Língua
Definition- Um idioma é um subconjunto de ∑ * para algum alfabeto ∑. Pode ser finito ou infinito.
Example - Se o idioma assumir todas as strings possíveis de comprimento 2 em ∑ = {a, b}, então L = {ab, aa, ba, bb}
O autômato finito pode ser classificado em dois tipos -
- Autômato Finito Determinístico (DFA)
- Autômato Finito Não Determinístico (NDFA / NFA)
Autômato Finito Determinístico (DFA)
No DFA, para cada símbolo de entrada, pode-se determinar o estado para o qual a máquina se moverá. Por isso, é chamadoDeterministic Automaton. Por ter um número finito de estados, a máquina é chamadaDeterministic Finite Machine ou Deterministic Finite Automaton.
Definição formal de um DFA
Um DFA pode ser representado por uma 5-tupla (Q, ∑, δ, q 0 , F) onde -
Q é um conjunto finito de estados.
∑ é um conjunto finito de símbolos chamado alfabeto.
δ é a função de transição onde δ: Q × ∑ → Q
q0é o estado inicial de onde qualquer entrada é processada (q 0 ∈ Q).
F é um conjunto de estados / estados finais de Q (F ⊆ Q).
Representação gráfica de um DFA
Um DFA é representado por dígrafos chamados state diagram.
- Os vértices representam os estados.
- Os arcos marcados com um alfabeto de entrada mostram as transições.
- O estado inicial é denotado por um único arco de entrada vazio.
- O estado final é indicado por círculos duplos.
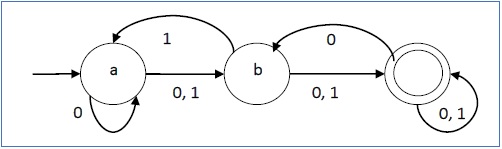
Exemplo
Seja um autômato finito determinístico →
- Q = {a, b, c},
- ∑ = {0, 1},
- q 0 = {a},
- F = {c}, e
Função de transição δ, conforme mostrado pela tabela a seguir -
| Estado atual | Próximo estado para a entrada 0 | Próximo estado para a entrada 1 |
|---|---|---|
| a | uma | b |
| b | c | uma |
| c | b | c |
Sua representação gráfica seria a seguinte -

No NDFA, para um símbolo de entrada específico, a máquina pode mover-se para qualquer combinação dos estados na máquina. Em outras palavras, o estado exato para o qual a máquina se move não pode ser determinado. Por isso, é chamadoNon-deterministic Automaton. Por possuir número finito de estados, a máquina é chamadaNon-deterministic Finite Machine ou Non-deterministic Finite Automaton.
Definição formal de um NDFA
Um NDFA pode ser representado por uma 5-tupla (Q, ∑, δ, q 0 , F) onde -
Q é um conjunto finito de estados.
∑ é um conjunto finito de símbolos chamados alfabetos.
δé a função de transição onde δ: Q × ∑ → 2 Q
(Aqui, o conjunto de potência de Q (2 Q ) foi tomado porque, no caso de NDFA, de um estado, a transição pode ocorrer para qualquer combinação de estados Q)
q0é o estado inicial de onde qualquer entrada é processada (q 0 ∈ Q).
F é um conjunto de estados / estados finais de Q (F ⊆ Q).
Representação gráfica de um NDFA: (igual ao DFA)
Um NDFA é representado por dígrafos chamados diagrama de estado.
- Os vértices representam os estados.
- Os arcos marcados com um alfabeto de entrada mostram as transições.
- O estado inicial é denotado por um único arco de entrada vazio.
- O estado final é indicado por círculos duplos.
Example
Seja um autômato finito não determinístico →
- Q = {a, b, c}
- ∑ = {0, 1}
- q 0 = {a}
- F = {c}
A função de transição δ conforme mostrado abaixo -
| Estado atual | Próximo estado para a entrada 0 | Próximo estado para a entrada 1 |
|---|---|---|
| uma | a, b | b |
| b | c | a, c |
| c | b, c | c |
Sua representação gráfica seria a seguinte -
DFA vs NDFA
A tabela a seguir lista as diferenças entre DFA e NDFA.
| DFA | NDFA |
|---|---|
| A transição de um estado é para um único próximo estado particular para cada símbolo de entrada. Por isso é chamado de determinístico . | A transição de um estado pode ser para vários próximos estados para cada símbolo de entrada. Por isso é chamado de não determinístico . |
| Transições de string vazias não são vistas no DFA. | NDFA permite transições de string vazias. |
| Retrocesso é permitido no DFA | No NDFA, o retrocesso nem sempre é possível. |
| Requer mais espaço. | Requer menos espaço. |
| Uma string é aceita por um DFA, se transitar para um estado final. | Uma string é aceita por um NDFA, se pelo menos uma de todas as transições possíveis terminar em um estado final. |
Aceitadores, classificadores e transdutores
Aceitador (Reconhecedor)
Um autômato que calcula uma função booleana é chamado de acceptor. Todos os estados de um aceitador estão aceitando ou rejeitando as entradas fornecidas a ele.
Classificador
UMA classifier tem mais de dois estados finais e fornece uma única saída quando termina.
Transdutor
Um autômato que produz saídas com base na entrada atual e / ou estado anterior é chamado de transducer. Os transdutores podem ser de dois tipos -
Mealy Machine - A saída depende do estado atual e da entrada atual.
Moore Machine - A saída depende apenas do estado atual.
Aceitabilidade por DFA e NDFA
Uma string é aceita por um DFA / NDFA iff o DFA / NDFA começando no estado inicial termina em um estado de aceitação (qualquer um dos estados finais) depois de ler a string completamente.
Uma string S é aceita por um DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S) ∈ F
O idioma L aceito pelo DFA / NDFA é
{S | S ∈ ∑* and δ*(q0, S) ∈ F}
Uma string S ′ não é aceita por um DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S′) ∉ F
O idioma L ′ não aceito pelo DFA / NDFA (Complemento do idioma L aceito) é
{S | S ∈ ∑* and δ*(q0, S) ∉ F}
Example
Vamos considerar o DFA mostrado na Figura 1.3. Do DFA, as strings aceitáveis podem ser derivadas.

Strings aceitos pelo DFA acima: {0, 00, 11, 010, 101, ...........}
Strings não aceitos pelo DFA acima: {1, 011, 111, ........}
Declaração do Problema
Deixei X = (Qx, ∑, δx, q0, Fx)ser um NDFA que aceita a linguagem L (X). Temos que projetar um DFA equivalenteY = (Qy, ∑, δy, q0, Fy) de tal modo que L(Y) = L(X). O procedimento a seguir converte o NDFA em seu DFA equivalente -
Algoritmo
Input - Um NDFA
Output - Um DFA equivalente
Step 1 - Crie uma tabela de estados a partir do NDFA fornecido.
Step 2 - Crie uma tabela de estados em branco em possíveis alfabetos de entrada para o DFA equivalente.
Step 3 - Marque o estado inicial do DFA por q0 (igual ao NDFA).
Step 4- Descubra a combinação de estados {Q 0 , Q 1 , ..., Q n } para cada alfabeto de entrada possível.
Step 5 - Cada vez que geramos um novo estado DFA nas colunas do alfabeto de entrada, temos que aplicar a etapa 4 novamente, caso contrário, vá para a etapa 6.
Step 6 - Os estados que contêm qualquer um dos estados finais do NDFA são os estados finais do DFA equivalente.
Exemplo
Vamos considerar o NDFA mostrado na figura abaixo.

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| uma | {a, b, c, d, e} | {d, e} |
| b | {c} | {e} |
| c | ∅ | {b} |
| d | {e} | ∅ |
| e | ∅ | ∅ |
Usando o algoritmo acima, encontramos seu DFA equivalente. A tabela de estado do DFA é mostrada a seguir.
| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| [uma] | [a, b, c, d, e] | [d, e] |
| [a, b, c, d, e] | [a, b, c, d, e] | [b, d, e] |
| [d, e] | [e] | ∅ |
| [b, d, e] | [c, e] | [e] |
| [e] | ∅ | ∅ |
| [c, e] | ∅ | [b] |
| [b] | [c] | [e] |
| [c] | ∅ | [b] |
O diagrama de estado do DFA é o seguinte -

Minimização DFA usando o teorema de Myhill-Nerode
Algoritmo
Input - DFA
Output - DFA minimizado
Step 1- Desenhe uma tabela para todos os pares de estados (Q i , Q j ) não necessariamente conectados diretamente [Todos são desmarcados inicialmente]
Step 2- Considere todos os pares de estados (Q i , Q j ) no DFA onde Q i ∈ F e Q j ∉ F ou vice-versa e marque-os. [Aqui F é o conjunto de estados finais]
Step 3 - Repita esta etapa até que não possamos marcar mais estados -
Se houver um par não marcado (Q i , Q j ), marque-o se o par {δ (Q i , A), δ (Q i , A)} estiver marcado para algum alfabeto de entrada.
Step 4- Combine todos os pares não marcados (Q i , Q j ) e torne-os um único estado no DFA reduzido.
Exemplo
Vamos usar o Algoritmo 2 para minimizar o DFA mostrado abaixo.

Step 1 - Desenhamos uma tabela para todos os pares de estados.
| uma | b | c | d | e | f | |
| uma | ||||||
| b | ||||||
| c | ||||||
| d | ||||||
| e | ||||||
| f |
Step 2 - Marcamos os pares de estados.
| uma | b | c | d | e | f | |
| uma | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ |
Step 3- Tentaremos marcar os pares de estados, com a marca de verificação de cor verde, transitivamente. Se inserirmos 1 no estado 'a' e 'f', ele irá para o estado 'c' e 'f' respectivamente. (c, f) já está marcado, portanto, marcaremos o par (a, f). Agora, inserimos 1 no estado 'b' e 'f'; ele irá para o estado 'd' e 'f' respectivamente. (d, f) já está marcado, portanto, marcaremos o par (b, f).
| uma | b | c | d | e | f | |
| uma | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ | ✔ | ✔ |
Após a etapa 3, temos as combinações de estado {a, b} {c, d} {c, e} {d, e} que não estão marcadas.
Podemos recombinar {c, d} {c, e} {d, e} em {c, d, e}
Portanto, temos dois estados combinados como - {a, b} e {c, d, e}
Portanto, o DFA minimizado final conterá três estados {f}, {a, b} e {c, d, e}
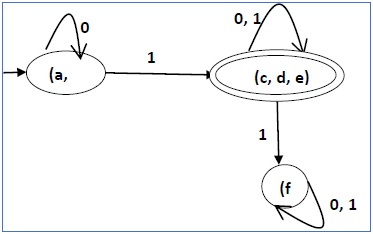
Minimização DFA usando o Teorema de Equivalência
Se X e Y são dois estados em um DFA, podemos combinar esses dois estados em {X, Y} se eles não forem distinguíveis. Dois estados são distinguíveis, se houver pelo menos uma string S, tal que um de δ (X, S) e δ (Y, S) está aceitando e outro não está aceitando. Conseqüentemente, um DFA é mínimo se e somente se todos os estados forem distinguíveis.
Algoritmo 3
Step 1 - todos os estados Q são divididos em duas partições - final states e non-final states e são denotados por P0. Todos os estados em uma partição são 0 th equivalente. Pegue um contadork e inicialize-o com 0.
Step 2- Incremente k em 1. Para cada partição em P k , divida os estados em P k em duas partições se eles forem k-distinguíveis. Dois estados dentro desta partição X e Y são k-distinguíveis se houver uma entradaS de tal modo que δ(X, S) e δ(Y, S) são (k-1) -distinguíveis.
Step 3- Se P k ≠ P k-1 , repita a Etapa 2, caso contrário, vá para a Etapa 4.
Step 4- Combine os k- ésimos conjuntos equivalentes e torne-os os novos estados do DFA reduzido.
Exemplo
Vamos considerar o seguinte DFA -

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| uma | b | c |
| b | uma | d |
| c | e | f |
| d | e | f |
| e | e | f |
| f | f | f |
Vamos aplicar o algoritmo acima ao DFA acima -
- P 0 = {(c, d, e), (a, b, f)}
- P 1 = {(c, d, e), (a, b), (f)}
- P 2 = {(c, d, e), (a, b), (f)}
Portanto, P 1 = P 2 .
Existem três estados no DFA reduzido. O DFA reduzido é o seguinte -
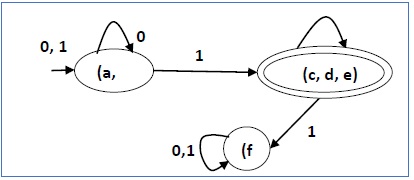
| Q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| (a, b) | (a, b) | (c, d, e) |
| (c, d, e) | (c, d, e) | (f) |
| (f) | (f) | (f) |
Autômatos finitos podem ter saídas correspondentes a cada transição. Existem dois tipos de máquinas de estado finito que geram saída -
- Mealy Machine
- Máquina de moore
Mealy Machine
Uma máquina Mealy é um FSM cuja saída depende do estado atual, bem como da entrada atual.
Pode ser descrito por uma tupla de 6 (Q, ∑, O, δ, X, q 0 ) onde -
Q é um conjunto finito de estados.
∑ é um conjunto finito de símbolos denominado alfabeto de entrada.
O é um conjunto finito de símbolos denominado alfabeto de saída.
δ é a função de transição de entrada onde δ: Q × ∑ → Q
X é a função de transição de saída onde X: Q × ∑ → O
q0é o estado inicial de onde qualquer entrada é processada (q 0 ∈ Q).
A tabela de estado de uma máquina Mealy é mostrada abaixo -
| Estado atual | Próximo estado | |||
|---|---|---|---|---|
| entrada = 0 | entrada = 1 | |||
| Estado | Resultado | Estado | Resultado | |
| → a | b | x 1 | c | x 1 |
| b | b | x 2 | d | x 3 |
| c | d | x 3 | c | x 1 |
| d | d | x 3 | d | x 2 |
O diagrama de estado da Mealy Machine acima é -

Máquina Moore
A máquina de Moore é um FSM cujas saídas dependem apenas do estado atual.
Uma máquina de Moore pode ser descrita por uma 6 tupla (Q, ∑, O, δ, X, q 0 ) onde -
Q é um conjunto finito de estados.
∑ é um conjunto finito de símbolos denominado alfabeto de entrada.
O é um conjunto finito de símbolos denominado alfabeto de saída.
δ é a função de transição de entrada onde δ: Q × ∑ → Q
X é a função de transição de saída onde X: Q → O
q0é o estado inicial de onde qualquer entrada é processada (q 0 ∈ Q).
A tabela de estado de uma Máquina Moore é mostrada abaixo -
| Estado atual | Próximo estado | Resultado | |
|---|---|---|---|
| Entrada = 0 | Entrada = 1 | ||
| → a | b | c | x 2 |
| b | b | d | x 1 |
| c | c | d | x 2 |
| d | d | d | x 3 |
O diagrama de estado da Máquina Moore acima é -

Máquina Mealy vs. Máquina Moore
A tabela a seguir destaca os pontos que diferenciam uma Máquina Mealy de uma Máquina Moore.
| Mealy Machine | Máquina Moore |
|---|---|
| A saída depende do estado atual e da entrada atual | A saída depende apenas do estado atual. |
| Geralmente, ele tem menos estados do que a Máquina Moore. | Geralmente, ele tem mais estados do que a Máquina Mealy. |
| O valor da função de saída é uma função das transições e mudanças, quando a lógica de entrada no estado atual é feita. | O valor da função de saída é uma função do estado atual e das mudanças nas bordas do clock, sempre que ocorrerem mudanças de estado. |
| As máquinas Mealy reagem mais rápido às entradas. Eles geralmente reagem no mesmo ciclo de clock. | Em máquinas Moore, mais lógica é necessária para decodificar as saídas, resultando em mais atrasos no circuito. Eles geralmente reagem um ciclo de clock depois. |
Máquina Moore para Máquina Mealy
Algoritmo 4
Input - Máquina Moore
Output - Máquina Mealy
Step 1 - Pegue um formato de tabela de transição da Máquina Mealy em branco.
Step 2 - Copie todos os estados de transição da Máquina Moore para este formato de tabela.
Step 3- Verifique os estados atuais e suas saídas correspondentes na tabela de estados da Máquina Moore; se para um estado Q i a saída for m, copie-o nas colunas de saída da tabela de estado da Máquina Mealy onde quer que Q i apareça no próximo estado.
Exemplo
Vamos considerar a seguinte máquina de Moore -
| Estado atual | Próximo estado | Resultado | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → a | d | b | 1 |
| b | uma | d | 0 |
| c | c | c | 0 |
| d | b | uma | 1 |
Agora aplicamos o Algoritmo 4 para convertê-lo em Máquina Mealy.
Step 1 & 2 -
| Estado atual | Próximo estado | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Estado | Resultado | Estado | Resultado | |
| → a | d | b | ||
| b | uma | d | ||
| c | c | c | ||
| d | b | uma | ||
Step 3 -
| Estado atual | Próximo estado | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Estado | Resultado | Estado | Resultado | |
| => a | d | 1 | b | 0 |
| b | uma | 1 | d | 1 |
| c | c | 0 | c | 0 |
| d | b | 0 | uma | 1 |
Máquina Mealy para Máquina Moore
Algoritmo 5
Input - Máquina Mealy
Output - Máquina Moore
Step 1- Calcule o número de saídas diferentes para cada estado (Q i ) que estão disponíveis na tabela de estados da máquina Mealy.
Step 2- Se todas as saídas de Qi forem iguais, copie o estado Q i . Se tiver n saídas distintas, divida Q i em n estados como Q em onden = 0, 1, 2 .......
Step 3 - Se a saída do estado inicial for 1, insira um novo estado inicial no início que forneça 0 saída.
Exemplo
Vamos considerar a seguinte Máquina Mealy -
| Estado atual | Próximo estado | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Próximo estado | Resultado | Próximo estado | Resultado | |
| → a | d | 0 | b | 1 |
| b | uma | 1 | d | 0 |
| c | c | 1 | c | 0 |
| d | b | 0 | uma | 1 |
Aqui, os estados 'a' e 'd' fornecem apenas 1 e 0 saídas, respectivamente, portanto, retemos os estados 'a' e 'd'. Mas os estados 'b' e 'c' produzem resultados diferentes (1 e 0). Então, nós dividimosb para dentro b0, b1 e c para dentro c0, c1.
| Estado atual | Próximo estado | Resultado | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → a | d | b 1 | 1 |
| b 0 | uma | d | 0 |
| b 1 | uma | d | 1 |
| c 0 | c 1 | C 0 | 0 |
| c 1 | c 1 | C 0 | 1 |
| d | b 0 | uma | 0 |
No sentido literário do termo, gramáticas denotam regras sintáticas para conversação em línguas naturais. A lingüística tem tentado definir gramáticas desde o início das línguas naturais, como inglês, sânscrito, mandarim, etc.
A teoria das linguagens formais encontra sua aplicabilidade extensivamente nos campos da Ciência da Computação. Noam Chomsky deu um modelo matemático de gramática em 1956 que é eficaz para escrever linguagens de computador.
Gramática
Uma gramática G pode ser formalmente escrito como uma tupla de 4 (N, T, S, P) onde -
N ou VN é um conjunto de variáveis ou símbolos não terminais.
T ou ∑ é um conjunto de símbolos Terminal.
S é uma variável especial chamada de símbolo inicial, S ∈ N
Psão as regras de produção para terminais e não terminais. Uma regra de produção tem a forma α → β, onde α e β são cordas em V N ∪ Σ e pelo menos um símbolo de α pertence a V N .
Exemplo
Grammar G1 -
({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})
Aqui,
S, A, e B são símbolos não terminais;
a e b são símbolos terminais
S é o símbolo de início, S ∈ N
Produções, P : S → AB, A → a, B → b
Exemplo
Grammar G2 -
(({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Aqui,
S e A são símbolos não terminais.
a e b são símbolos terminais.
ε é uma string vazia.
S é o símbolo de início, S ∈ N
Produção P : S → aAb, aA → aaAb, A → ε
Derivações de uma gramática
Strings podem ser derivadas de outras strings usando as produções em uma gramática. Se uma gramáticaG tem uma produção α → β, Nós podemos dizer que x α y deriva x β y dentro G. Esta derivação é escrita como -
x α y ⇒G x β y
Exemplo
Vamos considerar a gramática -
G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Algumas das strings que podem ser derivadas são -
S ⇒ aA b usando produção S → aAb
⇒ a aA bb usando produção aA → aAb
⇒ aaa A bbb usando produção aA → aAb
⇒ aaabbb usando produção A → ε
O conjunto de todas as strings que podem ser derivadas de uma gramática é considerado a linguagem gerada por essa gramática. Uma linguagem gerada por uma gramáticaG é um subconjunto formalmente definido por
L (G) = {W | W ∈ ∑ *, S ⇒ G W }
E se L(G1) = L(G2), a gramática G1 é equivalente à gramática G2.
Exemplo
Se houver uma gramática
G: N = {S, A, B} T = {a, b} P = {S → AB, A → a, B → b}
Aqui S produz AB, e podemos substituir A de a, e B de b. Aqui, a única string aceita éab, ou seja,
L (G) = {ab}
Exemplo
Suponha que temos a seguinte gramática -
G: N = {S, A, B} T = {a, b} P = {S → AB, A → aA | a, B → bB | b}
A linguagem gerada por esta gramática -
L (G) = {ab, a 2 b, ab 2 , a 2 b 2 , ………}
= {a m b n | m ≥ 1 e n ≥ 1}
Construção de uma gramática gerando uma linguagem
Vamos considerar algumas linguagens e convertê-las em uma gramática G que produz essas linguagens.
Exemplo
Problem- Suponha, L (G) = {a m b n | m ≥ 0 e n> 0}. Temos que descobrir a gramáticaG que produz L(G).
Solution
Como L (G) = {a m b n | m ≥ 0 e n> 0}
o conjunto de strings aceito pode ser reescrito como -
L (G) = {b, ab, bb, aab, abb, …….}
Aqui, o símbolo de início deve ter pelo menos um 'b' precedido por qualquer número de 'a' incluindo nulo.
Para aceitar o conjunto de strings {b, ab, bb, aab, abb, …….}, Pegamos as produções -
S → aS, S → B, B → be B → bB
S → B → b (aceito)
S → B → bB → bb (aceito)
S → aS → aB → ab (aceito)
S → aS → aaS → aaB → aab (aceito)
S → aS → aB → abB → abb (aceito)
Assim, podemos provar que cada string em L (G) é aceita pela linguagem gerada pelo conjunto de produção.
Daí a gramática -
G: ({S, A, B}, {a, b}, S, {S → aS | B, B → b | bB})
Exemplo
Problem- Suponha, L (G) = {a m b n | m> 0 e n ≥ 0}. Temos que descobrir a gramática G que produz L (G).
Solution -
Como L (G) = {a m b n | m> 0 e n ≥ 0}, o conjunto de strings aceito pode ser reescrito como -
L (G) = {a, aa, ab, aaa, aab, abb, …….}
Aqui, o símbolo de início deve ter pelo menos um 'a' seguido por qualquer número de 'b' incluindo nulo.
Para aceitar o conjunto de strings {a, aa, ab, aaa, aab, abb, …….}, Pegamos as produções -
S → aA, A → aA, A → B, B → bB, B → λ
S → aA → aB → aλ → a (aceito)
S → aA → aaA → aaB → aaλ → aa (aceito)
S → aA → aB → abB → abλ → ab (aceito)
S → aA → aaA → aaaA → aaaB → aaaλ → aaa (aceito)
S → aA → aaA → aaB → aabB → aabλ → aab (aceito)
S → aA → aB → abB → abbB → abbλ → abb (aceito)
Assim, podemos provar que cada string em L (G) é aceita pela linguagem gerada pelo conjunto de produção.
Daí a gramática -
G: ({S, A, B}, {a, b}, S, {S → aA, A → aA | B, B → λ | bB})
De acordo com Noam Chomosky, existem quatro tipos de gramáticas - Tipo 0, Tipo 1, Tipo 2 e Tipo 3. A tabela a seguir mostra como elas diferem umas das outras -
| Tipo de Gramática | Grammar Accepted | Idioma aceito | Autômato |
|---|---|---|---|
| Tipo 0 | Gramática irrestrita | Linguagem recursivamente enumerável | Máquina de Turing |
| Tipo 1 | Gramática sensível ao contexto | Linguagem sensível ao contexto | Autômato linear |
| Tipo 2 | Gramática livre de contexto | Linguagem livre de contexto | Autômato pushdown |
| Tipo 3 | Gramática regular | Linguagem regular | Autômato de estado finito |
Dê uma olhada na ilustração a seguir. Mostra o escopo de cada tipo de gramática -

Tipo - 3 gramática
Type-3 grammarsgerar linguagens regulares. As gramáticas do tipo 3 devem ter um único não terminal no lado esquerdo e um lado direito consistindo em um único terminal ou único terminal seguido por um único não terminal.
As produções devem estar no formato X → a or X → aY
Onde X, Y ∈ N (Não terminal)
e a ∈ T (Terminal)
A regra S → ε é permitido se S não aparece no lado direito de nenhuma regra.
Exemplo
X → ε
X → a | aY
Y → bTipo - 2 gramática
Type-2 grammars gerar linguagens livres de contexto.
As produções devem estar no formato A → γ
Onde A ∈ N (Não terminal)
e γ ∈ (T ∪ N)* (String de terminais e não terminais).
Essas linguagens geradas por essas gramáticas são reconhecidas por um autômato pushdown não determinístico.
Exemplo
S → X a
X → a
X → aX
X → abc
X → εTipo - 1 gramática
Type-1 grammarsgerar linguagens sensíveis ao contexto. As produções devem estar no formato
α A β → α γ β
Onde A ∈ N (Não terminal)
e α, β, γ ∈ (T ∪ N)* (Strings de terminais e não terminais)
As cordas α e β pode estar vazio, mas γ não deve estar vazio.
A regra S → εé permitido se S não aparecer no lado direito de nenhuma regra. As linguagens geradas por essas gramáticas são reconhecidas por um autômato linear limitado.
Exemplo
AB → AbBc
A → bcA
B → bTipo - 0 de gramática
Type-0 grammarsgerar linguagens recursivamente enumeráveis. As produções não têm restrições. Eles são qualquer gramática de estrutura de fase, incluindo todas as gramáticas formais.
Eles geram as linguagens que são reconhecidas por uma máquina de Turing.
As produções podem ser na forma de α → β Onde α é uma sequência de terminais e não terminais com pelo menos um não terminal e α não pode ser nulo. β é uma string de terminais e não terminais.
Exemplo
S → ACaB
Bc → acB
CB → DB
aD → DbUMA Regular Expression pode ser definido recursivamente da seguinte forma -
ε é uma expressão regular indica o idioma que contém uma string vazia. (L (ε) = {ε})
φ é uma expressão regular que denota um idioma vazio. (L (φ) = { })
x é uma expressão regular onde L = {x}
E se X é uma expressão regular que denota o idioma L(X) e Y é uma expressão regular que denota o idioma L(Y), então
X + Y é uma Expressão Regular correspondente ao idioma L(X) ∪ L(Y) Onde L(X+Y) = L(X) ∪ L(Y).
X . Y é uma Expressão Regular correspondente ao idioma L(X) . L(Y) Onde L(X.Y) = L(X) . L(Y)
R* é uma Expressão Regular correspondente ao idioma L(R*)Onde L(R*) = (L(R))*
Se aplicarmos qualquer uma das regras várias vezes de 1 a 5, elas serão expressões regulares.
Alguns exemplos de RE
| Expressões regulares | Conjunto Regular |
|---|---|
| (0 + 10 *) | L = {0, 1, 10, 100, 1000, 10000,…} |
| (0 * 10 *) | L = {1, 01, 10, 010, 0010,…} |
| (0 + ε) (1 + ε) | L = {ε, 0, 1, 01} |
| (a + b) * | Conjunto de strings de a's eb's de qualquer comprimento, incluindo a string nula. Então L = {ε, a, b, aa, ab, bb, ba, aaa …….} |
| (a + b) * abb | Conjunto de strings de a's eb's terminando com a string abb. Portanto, L = {abb, aabb, babb, aaabb, ababb, ………… ..} |
| (11) * | Conjunto consistindo em número par de 1's incluindo string vazia, So L = {ε, 11, 1111, 111111, ……….} |
| (aa) * (bb) * b | Conjunto de strings que consiste em número par de a's seguido por número ímpar de b's, então L = {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, ………… ..} |
| (aa + ab + ba + bb) * | Sequências de a's eb's de comprimento par podem ser obtidas concatenando qualquer combinação das strings aa, ab, ba e bb incluindo null, então L = {aa, ab, ba, bb, aaab, aaba, ………… .. } |
Qualquer conjunto que representa o valor da Expressão Regular é chamado de Regular Set.
Propriedades de conjuntos regulares
Property 1. A união de dois conjuntos regulares é regular.
Proof -
Vamos pegar duas expressões regulares
RE 1 = a (aa) * e RE 2 = (aa) *
Então, L 1 = {a, aaa, aaaaa, .....} (Strings de comprimento ímpar excluindo Null)
e L 2 = {ε, aa, aaaa, aaaaaa, .......} (cordas de comprimento par incluindo nulo)
L 1 ∪ L 2 = {ε, a, aa, aaa, aaaa, aaaaa, aaaaaa, .......}
(Strings de todos os comprimentos possíveis incluindo Null)
RE (L 1 ∪ L 2 ) = a * (que é uma expressão regular em si)
Hence, proved.
Property 2. A intersecção de dois conjuntos regulares é regular.
Proof −
Let us take two regular expressions
RE1 = a(a*) and RE2 = (aa)*
So, L1 = { a,aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∩ L2 = { aa, aaaa, aaaaaa,.......} (Strings of even length excluding Null)
RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.
Hence, proved.
Property 3. The complement of a regular set is regular.
Proof −
Let us take a regular expression −
RE = (aa)*
So, L = {ε, aa, aaaa, aaaaaa, .......} (Strings of even length including Null)
Complement of L is all the strings that is not in L.
So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)
RE (L’) = a(aa)* which is a regular expression itself.
Hence, proved.
Property 4. The difference of two regular set is regular.
Proof −
Let us take two regular expressions −
RE1 = a (a*) and RE2 = (aa)*
So, L1 = {a, aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}
(Strings of all odd lengths excluding Null)
RE (L1 – L2) = a (aa)* which is a regular expression.
Hence, proved.
Property 5. The reversal of a regular set is regular.
Proof −
We have to prove LR is also regular if L is a regular set.
Let, L = {01, 10, 11, 10}
RE (L) = 01 + 10 + 11 + 10
LR = {10, 01, 11, 01}
RE (LR) = 01 + 10 + 11 + 10 which is regular
Hence, proved.
Property 6. The closure of a regular set is regular.
Proof −
If L = {a, aaa, aaaaa, .......} (Strings of odd length excluding Null)
i.e., RE (L) = a (aa)*
L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)
RE (L*) = a (a)*
Hence, proved.
Property 7. The concatenation of two regular sets is regular.
Proof −
Let RE1 = (0+1)*0 and RE2 = 01(0+1)*
Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)
and L2 = {01, 010,011,.....} (Set of strings beginning with 01)
Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*
Hence, proved.
Identities Related to Regular Expressions
Given R, P, L, Q as regular expressions, the following identities hold −
- ∅* = ε
- ε* = ε
- RR* = R*R
- R*R* = R*
- (R*)* = R*
- RR* = R*R
- (PQ)*P =P(QP)*
- (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
- R + ∅ = ∅ + R = R (The identity for union)
- R ε = ε R = R (The identity for concatenation)
- ∅ L = L ∅ = ∅ (The annihilator for concatenation)
- R + R = R (Idempotent law)
- L (M + N) = LM + LN (Left distributive law)
- (M + N) L = ML + NL (Right distributive law)
- ε + RR* = ε + R*R = R*
In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.
Statement −
Let P and Q be two regular expressions.
If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*
Proof −
R = Q + (Q + RP)P [After putting the value R = Q + RP]
= Q + QP + RPP
When we put the value of R recursively again and again, we get the following equation −
R = Q + QP + QP2 + QP3…..
R = Q (ε + P + P2 + P3 + …. )
R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]
Hence, proved.
Assumptions for Applying Arden’s Theorem
- The transition diagram must not have NULL transitions
- It must have only one initial state
Method
Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q1.
q1 = q1R11 + q2R21 + … + qnRn1 + ε
q2 = q1R12 + q2R22 + … + qnRn2
…………………………
…………………………
…………………………
…………………………
qn = q1R1n + q2R2n + … + qnRnn
Rij represents the set of labels of edges from qi to qj, if no such edge exists, then Rij = ∅
Step 2 − Solve these equations to get the equation for the final state in terms of Rij
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state and final state is q1.
The equations for the three states q1, q2, and q3 are as follows −
q1 = q1a + q3a + ε (ε move is because q1 is the initial state0
q2 = q1b + q2b + q3b
q3 = q2a
Now, we will solve these three equations −
q2 = q1b + q2b + q3b
= q1b + q2b + (q2a)b (Substituting value of q3)
= q1b + q2(b + ab)
= q1b (b + ab)* (Applying Arden’s Theorem)
q1 = q1a + q3a + ε
= q1a + q2aa + ε (Substituting value of q3)
= q1a + q1b(b + ab*)aa + ε (Substituting value of q2)
= q1(a + b(b + ab)*aa) + ε
= ε (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
Hence, the regular expression is (a + b(b + ab)*aa)*.
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state is q1 and the final state is q2
Now we write down the equations −
q1 = q10 + ε
q2 = q11 + q20
q3 = q21 + q30 + q31
Now, we will solve these three equations −
q1 = ε0* [As, εR = R]
So, q1 = 0*
q2 = 0*1 + q20
So, q2 = 0*1(0)* [By Arden’s theorem]
Hence, the regular expression is 0*10*.
We can use Thompson's Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.
Some basic RA expressions are the following −
Case 1 − For a regular expression ‘a’, we can construct the following FA −

Case 2 − For a regular expression ‘ab’, we can construct the following FA −

Case 3 − For a regular expression (a+b), we can construct the following FA −

Case 4 − For a regular expression (a+b)*, we can construct the following FA −

Method
Step 1 Construct an NFA with Null moves from the given regular expression.
Step 2 Remove Null transition from the NFA and convert it into its equivalent DFA.
Problem
Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0
Solution
We will concatenate three expressions "1", "(0 + 1)*" and "0"

Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −

It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.
Finite Automata with Null Moves (NFA-ε)
A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move.
An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q0, F), consisting of
Q − a finite set of states
∑ − a finite set of input symbols
δ − a transition function δ : Q × (∑ ∪ {ε}) → 2Q
q0 − an initial state q0 ∈ Q
F − a set of final state/states of Q (F⊆Q).

The above (FA-ε) accepts a string set − {0, 1, 01}
Removal of Null Moves from Finite Automata
If in an NDFA, there is ϵ-move between vertex X to vertex Y, we can remove it using the following steps −
- Find all the outgoing edges from Y.
- Copy all these edges starting from X without changing the edge labels.
- If X is an initial state, make Y also an initial state.
- If Y is a final state, make X also a final state.
Problem
Convert the following NFA-ε to NFA without Null move.

Solution
Step 1 −
Here the ε transition is between q1 and q2, so let q1 is X and qf is Y.
Here the outgoing edges from qf is to qf for inputs 0 and 1.
Step 2 −
Now we will Copy all these edges from q1 without changing the edges from qf and get the following FA −

Step 3 −
Here q1 is an initial state, so we make qf also an initial state.
So the FA becomes −

Step 4 −
Here qf is a final state, so we make q1 also a final state.
So the FA becomes −

Theorem
Let L be a regular language. Then there exists a constant ‘c’ such that for every string w in L −
|w| ≥ c
We can break w into three strings, w = xyz, such that −
- |y| > 0
- |xy| ≤ c
- For all k ≥ 0, the string xykz is also in L.
Applications of Pumping Lemma
Pumping Lemma is to be applied to show that certain languages are not regular. It should never be used to show a language is regular.
If L is regular, it satisfies Pumping Lemma.
If L does not satisfy Pumping Lemma, it is non-regular.
Method to prove that a language L is not regular
At first, we have to assume that L is regular.
So, the pumping lemma should hold for L.
Use the pumping lemma to obtain a contradiction −
Select w such that |w| ≥ c
Select y such that |y| ≥ 1
Select x such that |xy| ≤ c
Assign the remaining string to z.
Select k such that the resulting string is not in L.
Hence L is not regular.
Problem
Prove that L = {aibi | i ≥ 0} is not regular.
Solution −
At first, we assume that L is regular and n is the number of states.
Let w = anbn. Thus |w| = 2n ≥ n.
By pumping lemma, let w = xyz, where |xy| ≤ n.
Let x = ap, y = aq, and z = arbn, where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
Let k = 2. Then xy2z = apa2qarbn.
Number of as = (p + 2q + r) = (p + q + r) + q = n + q
Hence, xy2z = an+q bn. Since q ≠ 0, xy2z is not of the form anbn.
Thus, xy2z is not in L. Hence L is not regular.
If (Q, ∑, δ, q0, F) be a DFA that accepts a language L, then the complement of the DFA can be obtained by swapping its accepting states with its non-accepting states and vice versa.
We will take an example and elaborate this below −

This DFA accepts the language
L = {a, aa, aaa , ............. }
over the alphabet
∑ = {a, b}
So, RE = a+.
Now we will swap its accepting states with its non-accepting states and vice versa and will get the following −

This DFA accepts the language
Ľ = {ε, b, ab ,bb,ba, ............... }
over the alphabet
∑ = {a, b}
Note − If we want to complement an NFA, we have to first convert it to DFA and then have to swap states as in the previous method.
Definition − A context-free grammar (CFG) consisting of a finite set of grammar rules is a quadruple (N, T, P, S) where
N is a set of non-terminal symbols.
T is a set of terminals where N ∩ T = NULL.
P is a set of rules, P: N → (N ∪ T)*, i.e., the left-hand side of the production rule P does have any right context or left context.
S is the start symbol.
Example
- The grammar ({A}, {a, b, c}, P, A), P : A → aA, A → abc.
- The grammar ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
- The grammar ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Generation of Derivation Tree
A derivation tree or parse tree is an ordered rooted tree that graphically represents the semantic information a string derived from a context-free grammar.
Representation Technique
Root vertex − Must be labeled by the start symbol.
Vertex − Labeled by a non-terminal symbol.
Leaves − Labeled by a terminal symbol or ε.
If S → x1x2 …… xn is a production rule in a CFG, then the parse tree / derivation tree will be as follows −

There are two different approaches to draw a derivation tree −
Top-down Approach −
Starts with the starting symbol S
Goes down to tree leaves using productions
Bottom-up Approach −
Starts from tree leaves
Proceeds upward to the root which is the starting symbol S
Derivation or Yield of a Tree
The derivation or the yield of a parse tree is the final string obtained by concatenating the labels of the leaves of the tree from left to right, ignoring the Nulls. However, if all the leaves are Null, derivation is Null.
Example
Let a CFG {N,T,P,S} be
N = {S}, T = {a, b}, Starting symbol = S, P = S → SS | aSb | ε
One derivation from the above CFG is “abaabb”
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Sentential Form and Partial Derivation Tree
A partial derivation tree is a sub-tree of a derivation tree/parse tree such that either all of its children are in the sub-tree or none of them are in the sub-tree.
Example
If in any CFG the productions are −
S → AB, A → aaA | ε, B → Bb| ε
the partial derivation tree can be the following −
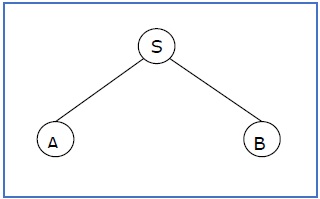
If a partial derivation tree contains the root S, it is called a sentential form. The above sub-tree is also in sentential form.
Leftmost and Rightmost Derivation of a String
Leftmost derivation − A leftmost derivation is obtained by applying production to the leftmost variable in each step.
Rightmost derivation − A rightmost derivation is obtained by applying production to the rightmost variable in each step.
Example
Let any set of production rules in a CFG be
X → X+X | X*X |X| a
over an alphabet {a}.
The leftmost derivation for the string "a+a*a" may be −
X → X+X → a+X → a + X*X → a+a*X → a+a*a
A derivação gradativa da string acima é mostrada abaixo -

A derivação mais à direita para a string acima "a+a*a" pode ser -
X → X * X → X * a → X + X * a → X + a * a → a + a * a
A derivação gradativa da string acima é mostrada abaixo -

Gramáticas recursivas esquerda e direita
Em uma gramática livre de contexto G, se houver uma produção no formulário X → Xa Onde X é um não terminal e ‘a’ é uma cadeia de terminais, é chamada de left recursive production. A gramática com uma produção recursiva à esquerda é chamada deleft recursive grammar.
E se em uma gramática livre de contexto G, se houver uma produção está na forma X → aX Onde X é um não terminal e ‘a’ é uma cadeia de terminais, é chamada de right recursive production. A gramática com uma produção recursiva correta é chamada deright recursive grammar.
Se uma gramática livre de contexto G tem mais de uma árvore de derivação para alguma string w ∈ L(G), é chamado de ambiguous grammar. Existem várias derivações mais à direita ou mais à esquerda para alguma string gerada a partir dessa gramática.
Problema
Verifique se a gramática G com regras de produção -
X → X + X | X * X | X | uma
é ambíguo ou não.
Solução
Vamos descobrir a árvore de derivação para a string "a + a * a". Possui duas derivações mais à esquerda.
Derivation 1- X → X + X → a + X → a + X * X → a + a * X → a + a * a
Parse tree 1 -

Derivation 2- X → X * X → X + X * X → a + X * X → a + a * X → a + a * a
Parse tree 2 -

Uma vez que existem duas árvores de análise para uma única string "a + a * a", a gramática G é ambíguo.
Linguagens livres de contexto são closed sob -
- Union
- Concatenation
- Operação Kleene Star
União
Sejam L 1 e L 2 duas linguagens livres de contexto. Então L 1 ∪ L 2 também é livre de contexto.
Exemplo
Seja L 1 = {a n b n , n> 0}. A gramática correspondente G 1 terá P: S1 → aAb | ab
Seja L 2 = {c m d m , m ≥ 0}. A gramática correspondente G 2 terá P: S2 → cBb | ε
União de L 1 e L 2 , L = L 1 ∪ L 2 = {a n b n } ∪ {c m d m }
A gramática G correspondente terá a produção adicional S → S1 | S2
Concatenação
Se L 1 e L 2 são linguagens livres de contexto, então L 1 L 2 também é livre de contexto.
Exemplo
União das línguas L 1 e L 2 , L = L 1 L 2 = {a n b n c m d m }
A gramática G correspondente terá a produção adicional S → S1 S2
Kleene Star
Se L é uma linguagem livre de contexto, então L * também é livre de contexto.
Exemplo
Seja L = {a n b n , n ≥ 0}. A gramática G correspondente terá P: S → aAb | ε
Kleene Star L 1 = {a n b n } *
A gramática correspondente G 1 terá produções adicionais S1 → SS 1 | ε
Linguagens livres de contexto são not closed sob -
Intersection - Se L1 e L2 são linguagens livres de contexto, então L1 ∩ L2 não é necessariamente livre de contexto.
Intersection with Regular Language - Se L1 é uma linguagem regular e L2 é uma linguagem livre de contexto, então L1 ∩ L2 é uma linguagem livre de contexto.
Complement - Se L1 for uma linguagem livre de contexto, então L1 'pode não ser livre de contexto.
Em uma CFG, pode acontecer que todas as regras de produção e símbolos não sejam necessários para a derivação de strings. Além disso, pode haver algumas produções nulas e produções unitárias. A eliminação dessas produções e símbolos é chamadasimplification of CFGs. A simplificação compreende essencialmente as seguintes etapas -
- Redução de CFG
- Remoção de unidades de produção
- Remoção de produções nulas
Redução de CFG
CFGs são reduzidos em duas fases -
Phase 1 - Derivação de uma gramática equivalente, G’, do CFG, G, de modo que cada variável derive alguma string terminal.
Derivation Procedure -
Etapa 1 - Incluir todos os símbolos, W1, que derivam algum terminal e inicializam i=1.
Etapa 2 - Incluir todos os símbolos, Wi+1, que derivam Wi.
Etapa 3 - Incremento i e repita a Etapa 2, até Wi+1 = Wi.
Etapa 4 - Incluir todas as regras de produção que têm Wi iniciar.
Phase 2 - Derivação de uma gramática equivalente, G”, do CFG, G’, de modo que cada símbolo apareça em uma forma sentencial.
Derivation Procedure -
Etapa 1 - Incluir o símbolo inicial em Y1 e inicializar i = 1.
Etapa 2 - Incluir todos os símbolos, Yi+1, que pode ser derivado de Yi e incluir todas as regras de produção que foram aplicadas.
Etapa 3 - Incremento i e repita a Etapa 2, até Yi+1 = Yi.
Problema
Encontre uma gramática reduzida equivalente à gramática G, com regras de produção, P: S → AC | B, A → a, C → c | BC, E → aA | e
Solução
Phase 1 -
T = {a, c, e}
W 1 = {A, C, E} das regras A → a, C → c e E → aA
W 2 = {A, C, E} U {S} da regra S → AC
W 3 = {A, C, E, S} U ∅
Como W 2 = W 3 , podemos derivar G 'como -
G '= {{A, C, E, S}, {a, c, e}, P, {S}}
onde P: S → AC, A → a, C → c, E → aA | e
Phase 2 -
Y 1 = {S}
Y 2 = {S, A, C} da regra S → AC
Y 3 = {S, A, C, a, c} das regras A → a e C → c
Y 4 = {S, A, C, a, c}
Uma vez que Y 3 = Y 4 , podemos derivar G ”como -
G ”= {{A, C, S}, {a, c}, P, {S}}
onde P: S → AC, A → a, C → c
Remoção de unidades de produção
Qualquer regra de produção na forma A → B onde A, B ∈ Não-terminal é chamada unit production..
Procedimento de Remoção -
Step 1 - Para remover A → B, adicionar produção A → x à regra gramatical sempre que B → xocorre na gramática. [x ∈ Terminal, x pode ser Nulo]
Step 2 - Apagar A → B da gramática.
Step 3 - Repita a partir do passo 1 até que todas as unidades de produção sejam removidas.
Problem
Remova a unidade de produção do seguinte -
S → XY, X → a, Y → Z | b, Z → M, M → N, N → a
Solution -
Existem 3 produções unitárias na gramática -
Y → Z, Z → M e M → N
At first, we will remove M → N.
Como N → a, adicionamos M → a, e M → N é removido.
O conjunto de produção torna-se
S → XY, X → a, Y → Z | b, Z → M, M → a, N → a
Now we will remove Z → M.
Como M → a, adicionamos Z → a, e Z → M é removido.
O conjunto de produção torna-se
S → XY, X → a, Y → Z | b, Z → a, M → a, N → a
Now we will remove Y → Z.
Como Z → a, adicionamos Y → a, e Y → Z é removido.
O conjunto de produção torna-se
S → XY, X → a, Y → a | b, Z → a, M → a, N → a
Agora Z, M e N estão inacessíveis, portanto, podemos removê-los.
O CFG final é uma unidade de produção livre -
S → XY, X → a, Y → a | b
Remoção de produções nulas
Em um CFG, um símbolo não terminal ‘A’ é uma variável anulável se houver uma produção A → ε ou há uma derivação que começa em A e finalmente termina com
ε: A → .......… → ε
Procedimento de Remoção
Step 1 - Descubra variáveis não terminais anuláveis que derivam ε.
Step 2 - Para cada produção A → a, construir todas as produções A → x Onde x é obtido de ‘a’ removendo um ou vários não terminais da Etapa 1.
Step 3 - Combine as produções originais com o resultado da etapa 2 e remova ε - productions.
Problem
Remova a produção nula do seguinte -
S → ASA | aB | b, A → B, B → b | ∈
Solution -
Existem duas variáveis anuláveis - A e B
At first, we will remove B → ε.
Depois de remover B → ε, o conjunto de produção se torna -
S → ASA | aB | b | a, A ε B | b | & épsilon, B → b
Now we will remove A → ε.
Depois de remover A → ε, o conjunto de produção se torna -
S → ASA | aB | b | a | SA | AS | S, A → B | b, B → b
Este é o conjunto de produção final sem transição nula.
Um CFG está na forma normal de Chomsky se as produções estiverem nas seguintes formas -
- A → a
- A → BC
- S → ε
onde A, B e C são não terminais e a é terminal.
Algoritmo para converter para a forma normal de Chomsky -
Step 1 - Se o símbolo de início S ocorre em algum lado direito, crie um novo símbolo de início S’ e uma nova produção S’→ S.
Step 2- Remova produções nulas. (Usando o algoritmo de remoção de produção nula discutido anteriormente)
Step 3- Remova produções unitárias. (Usando o algoritmo de remoção de produção da unidade discutido anteriormente)
Step 4 - Substitua cada produção A → B1…Bn Onde n > 2 com A → B1C Onde C → B2 …Bn. Repita esta etapa para todas as produções com dois ou mais símbolos no lado direito.
Step 5 - Se o lado direito de qualquer produção estiver na forma A → aB onde a é um terminal e A, B não são terminais, então a produção é substituída por A → XB e X → a. Repita esta etapa para cada produção que está no formulárioA → aB.
Problema
Converta o seguinte CFG em CNF
S → ASA | aB, A → B | S, B → b | ε
Solução
(1) Desde a S aparece no RHS, adicionamos um novo estado S0 e S0→S é adicionado ao conjunto de produção e se torna -
S 0 → S, S → ASA | aB, A → B | S, B → b | ∈
(2) Agora vamos remover as produções nulas -
B → ∈ e A → ∈
Depois de remover B → ε, o conjunto de produção se torna -
S 0 → S, S → ASA | aB | a, A → B | S | ∈, B → b
Depois de remover A → ∈, o conjunto de produção se torna -
S 0 → S, S → ASA | aB | a | AS | SA | S, A → B | S, B → b
(3) Agora vamos remover as produções unitárias.
Depois de remover S → S, o conjunto de produção se torna -
S 0 → S, S → ASA | aB | a | AS | SA, A → B | S, B → b
Depois de remover S 0 → S, o conjunto de produção torna-se -
S 0 → ASA | aB | a | AS | SA, S → ASA | aB | a | AS | SA
A → B | S, B → b
Depois de remover A → B, o conjunto de produção se torna -
S 0 → ASA | aB | a | AS | SA, S → ASA | aB | a | AS | SA
A → S | b
B → b
Depois de remover A → S, o conjunto de produção se torna -
S 0 → ASA | aB | a | AS | SA, S → ASA | aB | a | AS | SA
A → b | ASA | aB | a | AS | SA, B → b
(4) Agora vamos descobrir mais de duas variáveis no RHS
Aqui, S 0 → ASA, S → ASA, A → ASA viola dois não terminais em RHS
Portanto, aplicaremos as etapas 4 e 5 para obter o seguinte conjunto de produção final que está em CNF -
S 0 → AX | aB | a | AS | SA
S → AX | aB | a | AS | SA
A → b | AX | aB | a | AS | SA
B → b
X → SA
(5)Temos que mudar as produções S 0 → aB, S → aB, A → aB
E o conjunto de produção final se torna -
S 0 → AX | YB | a | AS | SA
S → AX | YB | a | AS | SA
A → b A → b | AX | YB | a | AS | SA
B → b
X → SA
S → a
Um CFG está na forma normal de Greibach se as produções estiverem nas seguintes formas -
A → b
A → bD 1 ... D n
S → ε
onde A, D 1 , ...., D n são não terminais eb é um terminal.
Algoritmo para converter um CFG na forma normal de Greibach
Step 1 - Se o símbolo de início S ocorre em algum lado direito, crie um novo símbolo de início S’ e uma nova produção S’ → S.
Step 2- Remova produções nulas. (Usando o algoritmo de remoção de produção nula discutido anteriormente)
Step 3- Remova produções unitárias. (Usando o algoritmo de remoção de produção da unidade discutido anteriormente)
Step 4 - Remova toda a recursão à esquerda direta e indireta.
Step 5 - Faça substituições adequadas de produções para convertê-lo na forma adequada de GNF.
Problema
Converta o seguinte CFG em CNF
S → XY | Xn | p
X → mX | m
Y → Xn | o
Solução
Aqui, Snão aparece no lado direito de nenhuma produção e não há unidades ou produções nulas no conjunto de regras de produção. Portanto, podemos pular da Etapa 1 para a Etapa 3.
Step 4
Agora depois de substituir
X em S → XY | Xo | p
com
mX | m
nós obtemos
S → mXY | mY | mXo | mo | p.
E depois de substituir
X em Y → X n | o
com o lado direito de
X → mX | m
nós obtemos
Y → mXn | mn | o.
Duas novas produções O → o e P → p são adicionadas ao conjunto de produção e então chegamos ao GNF final da seguinte forma -
S → mXY | mY | mXC | mC | p
X → mX | m
Y → mXD | mD | o
O → o
P → p
Lema
E se L é uma linguagem livre de contexto, há um comprimento de bombeamento p de modo que qualquer corda w ∈ L de comprimento ≥ p pode ser escrito como w = uvxyz, Onde vy ≠ ε, |vxy| ≤ p, e para todos i ≥ 0, uvixyiz ∈ L.
Aplicações do Lema de Bombeamento
O lema do bombeamento é usado para verificar se uma gramática é livre de contexto ou não. Vamos dar um exemplo e mostrar como ele é verificado.
Problema
Descubra se o idioma L = {xnynzn | n ≥ 1} é livre de contexto ou não.
Solução
Deixei Lé livre de contexto. Então,L deve satisfazer o lema do bombeamento.
Primeiro, escolha um número ndo lema do bombeamento. Então, considere z como 0 n 1 n 2 n .
Pausa z para dentro uvwxy, Onde
|vwx| ≤ n and vx ≠ ε.
Conseqüentemente vwxnão pode envolver 0s e 2s, uma vez que o último 0 e os primeiros 2 estão separados por pelo menos (n + 1) posições. Existem dois casos -
Case 1 - vwxnão tem 2s. Entãovxtem apenas 0s e 1s. Entãouwy, que teria que estar em L, tem n 2s, mas menos do que n 0s ou 1s.
Case 2 - vwx não tem 0s.
Aqui ocorre contradição.
Conseqüentemente, L não é uma linguagem livre de contexto.
Estrutura Básica do PDA
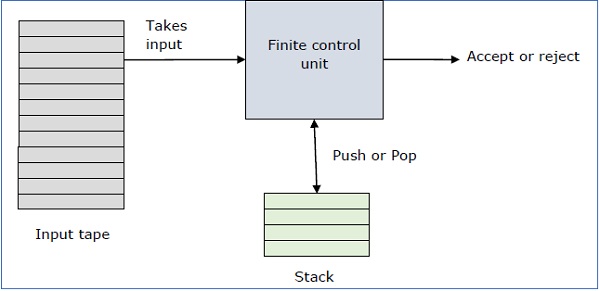
Um autômato pushdown é uma maneira de implementar uma gramática livre de contexto de uma maneira semelhante à qual projetamos o DFA para uma gramática regular. Um DFA pode lembrar uma quantidade finita de informações, mas um PDA pode lembrar uma quantidade infinita de informações.
Basicamente, um autômato pushdown é -
"Finite state machine" + "a stack"
Um autômato pushdown tem três componentes -
- uma fita de entrada,
- uma unidade de controle, e
- uma pilha com tamanho infinito.
O cabeçalho da pilha examina o símbolo do topo da pilha.
Uma pilha faz duas operações -
Push - um novo símbolo é adicionado no topo.
Pop - o símbolo superior é lido e removido.
Um PDA pode ou não ler um símbolo de entrada, mas precisa ler o topo da pilha em cada transição.
Um PDA pode ser formalmente descrito como um 7-tupla (Q, ∑, S, δ, q 0 , I, F) -
Q é o número finito de estados
∑ é o alfabeto de entrada
S são símbolos de pilha
δ é a função de transição: Q × (∑ ∪ {ε}) × S × Q × S *
q0é o estado inicial (q 0 ∈ Q)
I é o símbolo inicial do topo da pilha (I ∈ S)
F é um conjunto de estados de aceitação (F ∈ Q)
O diagrama a seguir mostra uma transição em um PDA de um estado q 1 para o estado q 2 , rotulado como a, b → c -

Isso significa no estado q1, se encontrarmos uma string de entrada ‘a’ e o símbolo do topo da pilha é ‘b’, então nós estouramos ‘b’, empurrar ‘c’ no topo da pilha e mova para o estado q2.
Terminologias relacionadas ao PDA
Descrição Instantânea
A descrição instantânea (ID) de um PDA é representada por um tripleto (q, w, s) onde
q é o estado
w é entrada não consumida
s é o conteúdo da pilha
Notação de torniquete
A notação "catraca" é usada para conectar pares de IDs que representam um ou vários movimentos de um PDA. O processo de transição é denotado pelo símbolo da catraca "⊢".
Considere um PDA (Q, ∑, S, δ, q 0 , I, F). Uma transição pode ser representada matematicamente pela seguinte notação de catraca -
(p, aw, Tβ) ⊢ (q, w, αb)Isso implica que, embora haja uma transição do estado p declarar q, o símbolo de entrada ‘a’ é consumido, e o topo da pilha ‘T’ é substituído por uma nova string ‘α’.
Note - Se quisermos zero ou mais movimentos de um PDA, temos que usar o símbolo (⊢ *) para isso.
Existem duas maneiras diferentes de definir a aceitabilidade do PDA.
Aceitabilidade do estado final
Na aceitabilidade do estado final, um PDA aceita uma string quando, depois de ler a string inteira, o PDA está em um estado final. Do estado inicial, podemos fazer movimentos que terminam em um estado final com quaisquer valores da pilha. Os valores da pilha são irrelevantes, contanto que acabemos em um estado final.
Para um PDA (Q, ∑, S, δ, q 0 , I, F), a linguagem aceita pelo conjunto de estados finais F é -
L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, x), q ∈ F}
para qualquer string de pilha de entrada x.
Aceitabilidade de pilha vazia
Aqui, um PDA aceita uma string quando, depois de ler a string inteira, o PDA esvazia sua pilha.
Para um PDA (Q, ∑, S, δ, q 0 , I, F), a linguagem aceita pela pilha vazia é -
L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, ε), q ∈ Q}
Exemplo
Construa um PDA que aceite L = {0n 1n | n ≥ 0}
Solução

Este idioma aceita L = {ε, 01, 0011, 000111, .............................}
Aqui, neste exemplo, o número de ‘a’ e ‘b’ tem que ser o mesmo.
Inicialmente, colocamos um símbolo especial ‘$’ na pilha vazia.
Então no estado q2, se encontrarmos a entrada 0 e o topo for Nulo, colocamos 0 na pilha. Isso pode iterar. E se encontrarmos a entrada 1 e o topo for 0, colocaremos este 0.
Então no estado q3, se encontrarmos a entrada 1 e o topo for 0, estouramos este 0. Isso também pode iterar. E se encontrarmos a entrada 1 e o topo for 0, exibimos o elemento superior.
Se o símbolo especial '$' for encontrado no topo da pilha, ele é retirado e finalmente vai para o estado de aceitação q 4 .
Exemplo
Construa um PDA que aceite L = {ww R | w = (a + b) *}
Solution

Inicialmente, colocamos um símbolo especial '$' na pilha vazia. No estadoq2, a westá sendo lido. No estadoq3, cada 0 ou 1 é exibido quando corresponder à entrada. Se qualquer outra entrada for fornecida, o PDA irá para um estado morto. Quando alcançamos aquele símbolo especial '$', vamos para o estado de aceitaçãoq4.
Se uma gramática G é livre de contexto, podemos construir um PDA não determinístico equivalente que aceita a linguagem que é produzida pela gramática livre de contexto G. Um analisador pode ser construído para a gramáticaG.
Também se P é um autômato pushdown, uma gramática livre de contexto equivalente G pode ser construída onde
L(G) = L(P)
Nos próximos dois tópicos, discutiremos como converter de PDA para CFG e vice-versa.
Algoritmo para encontrar PDA correspondente a um determinado CFG
Input - A CFG, G = (V, T, P, S)
Output- PDA equivalente, P = (Q, ∑, S, δ, q 0 , I, F)
Step 1 - Converter as produções do CFG em GNF.
Step 2 - O PDA terá apenas um estado {q}.
Step 3 - O símbolo de início de CFG será o símbolo de início no PDA.
Step 4 - Todos os não terminais do CFG serão os símbolos da pilha do PDA e todos os terminais do CFG serão os símbolos de entrada do PDA.
Step 5 - Para cada produção no formulário A → aX onde a é terminal e A, X são uma combinação de terminais e não terminais, faça uma transição δ (q, a, A).
Problema
Construa um PDA a partir do seguinte CFG.
G = ({S, X}, {a, b}, P, S)
onde as produções estão -
S → XS | ε , A → aXb | Ab | ab
Solução
Deixe o PDA equivalente,
P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)
onde δ -
δ (q, ε, S) = {(q, XS), (q, ε)}
δ (q, ε, X) = {(q, aXb), (q, Xb), (q, ab)}
δ (q, a, a) = {(q, ε)}
δ (q, 1, 1) = {(q, ε)}
Algoritmo para encontrar CFG correspondente a um determinado PDA
Input - A CFG, G = (V, T, P, S)
Output- PDA equivalente, P = (Q, ∑, S, δ, q 0 , I, F) tal que os não terminais da gramática G serão {X wx | w, x ∈ Q} e o estado inicial será Um q0, F .
Step 1- Para cada w, x, y, z ∈ Q, m ∈ S e a, b ∈ ∑, se δ (w, a, ε) contém (y, m) e (z, b, m) contém (x, ε), adicione a regra de produção X wx → a X yz b na gramática G.
Step 2- Para cada w, x, y, z ∈ Q, adicione a regra de produção X wx → X wy X yx na gramática G.
Step 3- Para w ∈ Q, adicione a regra de produção X ww → ε na gramática G.
A análise é usada para derivar uma string usando as regras de produção de uma gramática. É usado para verificar a aceitabilidade de uma string. O compilador é usado para verificar se uma string está sintaticamente correta ou não. Um analisador pega as entradas e constrói uma árvore de análise.
Um analisador pode ser de dois tipos -
Top-Down Parser - A análise de cima para baixo começa do topo com o símbolo de início e deriva uma string usando uma árvore de análise.
Bottom-Up Parser - A análise de baixo para cima começa de baixo para cima com a string e chega ao símbolo inicial usando uma árvore de análise.
Projeto do analisador de cima para baixo
Para análise de cima para baixo, um PDA tem os seguintes quatro tipos de transições -
Estale o não terminal do lado esquerdo da produção no topo da pilha e empurre seu fio do lado direito.
Se o símbolo do topo da pilha corresponder ao símbolo de entrada que está sendo lido, retire-o.
Empurre o símbolo inicial 'S' na pilha.
Se a string de entrada for totalmente lida e a pilha estiver vazia, vá para o estado final 'F'.
Exemplo
Projete um analisador de cima para baixo para a expressão "x + y * z" para a gramática G com as seguintes regras de produção -
P: S → S + X | X, X → X * Y | Y, Y → (S) | Eu iria
Solution
Se o PDA for (Q, ∑, S, δ, q 0 , I, F), então a análise de cima para baixo é -
(x + y * z, I) ⊢ (x + y * z, SI) ⊢ (x + y * z, S + XI) ⊢ (x + y * z, X + XI)
⊢ (x + y * z, Y + XI) ⊢ (x + y * z, x + XI) ⊢ (+ y * z, + XI) ⊢ (y * z, XI)
⊢ (y * z, X * YI) ⊢ (y * z, y * YI) ⊢ (* z, * YI) ⊢ (z, YI) ⊢ (z, zI) ⊢ (ε, I)
Projeto de um analisador de baixo para cima
Para análise ascendente, um PDA tem os seguintes quatro tipos de transições -
Empurre o símbolo de entrada atual na pilha.
Substitua o lado direito de uma produção no topo da pilha pelo lado esquerdo.
Se o topo do elemento da pilha corresponder ao símbolo de entrada atual, destaque-o.
Se a string de entrada for totalmente lida e somente se o símbolo inicial 'S' permanecer na pilha, retire-o e vá para o estado final 'F'.
Exemplo
Projete um analisador de cima para baixo para a expressão "x + y * z" para a gramática G com as seguintes regras de produção -
P: S → S + X | X, X → X * Y | Y, Y → (S) | Eu iria
Solution
Se o PDA for (Q, ∑, S, δ, q 0 , I, F), então a análise de baixo para cima é -
(x + y * z, I) ⊢ (+ y * z, xI) ⊢ (+ y * z, YI) ⊢ (+ y * z, XI) ⊢ (+ y * z, SI)
⊢ (y * z, + SI) ⊢ (* z, y + SI) ⊢ (* z, Y + SI) ⊢ (* z, X + SI) ⊢ (z, * X + SI)
⊢ (ε, z * X + SI) ⊢ (ε, Y * X + SI) ⊢ (ε, X + SI) ⊢ (ε, SI)
Uma Máquina de Turing é um dispositivo de aceitação que aceita as linguagens (conjunto recursivamente enumerável) geradas por gramáticas do tipo 0. Foi inventado em 1936 por Alan Turing.
Definição
Uma Máquina de Turing (TM) é um modelo matemático que consiste em uma fita de comprimento infinito dividida em células nas quais a entrada é dada. Consiste em uma cabeça que lê a fita de entrada. Um registro de estado armazena o estado da máquina de Turing. Depois de ler um símbolo de entrada, ele é substituído por outro símbolo, seu estado interno é alterado e ele se move de uma célula para a direita ou esquerda. Se a TM atinge o estado final, a string de entrada é aceita, caso contrário, rejeitada.
A TM pode ser formalmente descrita como uma 7-tupla (Q, X, ∑, δ, q 0 , B, F) onde -
Q é um conjunto finito de estados
X é o alfabeto da fita
∑ é o alfabeto de entrada
δé uma função de transição; δ: Q × X → Q × X × {Left_shift, Right_shift}.
q0 é o estado inicial
B é o símbolo em branco
F é o conjunto de estados finais
Comparação com o autômato anterior
A tabela a seguir mostra uma comparação de como uma máquina de Turing difere do Autômato Finito e do Autômato Pushdown.
| Máquina | Estrutura de dados da pilha | Determinístico? |
|---|---|---|
| Autômato Finito | N / D | sim |
| Pushdown Automaton | Último a entrar, primeiro a sair (UEPS) | Não |
| Máquina de Turing | Fita infinita | sim |
Exemplo de máquina de Turing
Máquina de Turing M = (Q, X, ∑, δ, q 0 , B, F) com
- Q = {q 0 , q 1 , q 2 , q f }
- X = {a, b}
- ∑ = {1}
- q 0 = {q 0 }
- B = símbolo em branco
- F = {q f }
δ é dado por -
| Símbolo do alfabeto de fita | Estado Atual 'q 0 ' | Estado Atual 'q 1 ' | Estado Atual 'q 2 ' |
|---|---|---|---|
| uma | 1Rq 1 | 1Lq 0 | 1Lq f |
| b | 1Lq 2 | 1Rq 1 | 1Rq f |
Aqui, a transição 1Rq 1 implica que o símbolo de gravação é 1, a fita se move para a direita e o próximo estado é q 1 . Da mesma forma, a transição 1Lq 2 implica que o símbolo de gravação é 1, a fita se move para a esquerda e o próximo estado é q 2 .
Complexidade de tempo e espaço de uma máquina de Turing
Para uma máquina de Turing, a complexidade do tempo refere-se à medida do número de vezes que a fita se move quando a máquina é inicializada para alguns símbolos de entrada e a complexidade do espaço é o número de células da fita gravada.
Complexidade de tempo, todas as funções razoáveis -
T(n) = O(n log n)
A complexidade do espaço da TM -
S(n) = O(n)
Uma TM aceita um idioma se entrar em um estado final para qualquer string de entrada w. Uma linguagem é recursivamente enumerável (gerada pela gramática Tipo-0) se for aceita por uma máquina de Turing.
Uma TM decide se um idioma o aceita e entra em um estado de rejeição para qualquer entrada que não esteja no idioma. Uma linguagem é recursiva se for decidida por uma máquina de Turing.
Pode haver alguns casos em que uma MT não para. Essa MT aceita o idioma, mas não o decide.
Projetando uma Máquina de Turing
As diretrizes básicas para projetar uma máquina de Turing foram explicadas abaixo com a ajuda de alguns exemplos.
Exemplo 1
Projete uma TM para reconhecer todas as cadeias que consistem em um número ímpar de αs.
Solution
A máquina de Turing M pode ser construído pelos seguintes movimentos -
Deixei q1 ser o estado inicial.
E se M é em q1; na varredura α, ele entra no estadoq2 e escreve B (em branco).
E se M é em q2; na varredura α, ele entra no estadoq1 e escreve B (em branco).
A partir dos movimentos acima, podemos ver que M entra no estado q1 se varre um número par de α's, e entra no estado q2se varre um número ímpar de α's. Conseqüentementeq2 é o único estado de aceitação.
Conseqüentemente,
M = {{q 1 , q 2 }, {1}, {1, B}, δ, q 1 , B, {q 2 }}
onde δ é dado por -
| Símbolo do alfabeto de fita | Estado Atual 'q 1 ' | Estado Atual 'q 2 ' |
|---|---|---|
| α | BRq 2 | BRq 1 |
Exemplo 2
Projete uma máquina de Turing que leia uma string representando um número binário e apague todos os zeros iniciais da string. No entanto, se a string for composta por apenas 0s, ela manterá um 0.
Solution
Vamos supor que a string de entrada é encerrada por um símbolo em branco, B, em cada extremidade da string.
A Máquina de Turing, M, pode ser construído pelos seguintes movimentos -
Deixei q0 ser o estado inicial.
E se M é em q0, na leitura 0, move-se para a direita, entra no estado q1 e apaga 0. Na leitura 1, ele entra no estado q2 e se move para a direita.
E se M é em q1, na leitura 0, move-se para a direita e apaga 0, ou seja, substitui 0's por B's. Ao chegar ao 1 mais à esquerda, ele entraq2e se move para a direita. Se atingir B, ou seja, a string é composta por apenas 0's, ela se move para a esquerda e entra no estadoq3.
E se M é em q2, ao ler 0 ou 1, ele se move para a direita. Ao chegar a B, ele se move para a esquerda e entra no estadoq4. Isso valida que a string compreende apenas 0's e 1's.
E se M é em q3, ele substitui B por 0, move-se para a esquerda e atinge o estado final qf.
E se M é em q4, ao ler 0 ou 1, ele se move para a esquerda. Ao chegar ao início da string, ou seja, ao ler B, chega ao estado finalqf.
Conseqüentemente,
M = {{q 0 , q 1 , q 2 , q 3 , q 4 , q f }, {0,1, B}, {1, B}, δ, q 0 , B, {q f }}
onde δ é dado por -
| Símbolo do alfabeto de fita | Estado Atual 'q 0 ' | Estado Atual 'q 1 ' | Estado Atual 'q 2 ' | Estado Atual 'q 3 ' | Estado Atual 'q 4 ' |
|---|---|---|---|---|---|
| 0 | BRq 1 | BRq 1 | ORq 2 | - | OLq 4 |
| 1 | 1Rq 2 | 1Rq 2 | 1Rq 2 | - | 1Lq 4 |
| B | BRq 1 | BLq 3 | BLq 4 | OLq f | BRq f |
As máquinas de Turing com várias fitas têm várias fitas, onde cada fita é acessada com um cabeçote separado. Cada cabeça pode se mover independentemente das outras cabeças. Inicialmente a entrada está na fita 1 e as outras estão em branco. A princípio, a primeira fita é ocupada pela entrada e as demais fitas são mantidas em branco. Em seguida, a máquina lê símbolos consecutivos sob suas cabeças e a TM imprime um símbolo em cada fita e move suas cabeças.

Uma máquina de Turing Multi-tape pode ser formalmente descrita como uma 6-tupla (Q, X, B, δ, q 0 , F) onde -
Q é um conjunto finito de estados
X é o alfabeto da fita
B é o símbolo em branco
δ é uma relação sobre estados e símbolos onde
δ: Q × X k → Q × (X × {Left_shift, Right_shift, No_shift}) k
onde há k número de fitas
q0 é o estado inicial
F é o conjunto de estados finais
Note - Cada máquina de Turing de fita múltipla tem uma máquina de Turing de fita única equivalente.
As máquinas de Turing com várias trilhas, um tipo específico de máquina de Turing com várias fitas, contêm várias trilhas, mas apenas uma cabeça de fita lê e grava em todas as trilhas. Aqui, uma única cabeça de fita lê n símbolos denfaixas em uma etapa. Ele aceita linguagens recursivamente enumeráveis como uma Turing Machine de faixa única normal aceita.
Uma máquina de Turing Multi-track pode ser formalmente descrita como uma 6-tupla (Q, X, ∑, δ, q 0 , F) onde -
Q é um conjunto finito de estados
X é o alfabeto da fita
∑ é o alfabeto de entrada
δ é uma relação sobre estados e símbolos onde
δ (Q i , [a 1 , a 2 , a 3 , ....]) = (Q j , [b 1 , b 2 , b 3 , ....], Left_shift ou Right_shift)
q0 é o estado inicial
F é o conjunto de estados finais
Note - Para cada máquina de Turing de pista única S, há uma Máquina de Turing multitrilha equivalente M de tal modo que L(S) = L(M).
Em uma Máquina de Turing Não Determinística, para cada estado e símbolo, há um grupo de ações que a MT pode ter. Então, aqui as transições não são determinísticas. O cálculo de uma Máquina de Turing não determinística é uma árvore de configurações que pode ser alcançada desde a configuração inicial.
Uma entrada é aceita se houver pelo menos um nó da árvore que seja uma configuração aceita, caso contrário, não é aceita. Se todos os ramos da árvore computacional param em todas as entradas, a Máquina de Turing não determinística é chamada deDecider e se para alguma entrada, todas as ramificações forem rejeitadas, a entrada também será rejeitada.
Uma máquina de Turing não determinística pode ser definida formalmente como uma 6-tupla (Q, X, ∑, δ, q 0 , B, F) onde -
Q é um conjunto finito de estados
X é o alfabeto da fita
∑ é o alfabeto de entrada
δ é uma função de transição;
δ: Q × X → P (Q × X × {Left_shift, Right_shift}).
q0 é o estado inicial
B é o símbolo em branco
F é o conjunto de estados finais
Uma Máquina de Turing com uma fita semi-infinita tem uma extremidade esquerda, mas não uma extremidade direita. A extremidade esquerda é limitada com um marcador final.

É uma fita de duas trilhas -
Upper track - Representa as células à direita da posição inicial da cabeça.
Lower track - Representa as células à esquerda da posição inicial da cabeça na ordem inversa.
A string de entrada de comprimento infinito é inicialmente gravada na fita em células de fita contíguas.
A máquina começa do estado inicial q0e a cabeça faz a varredura do marcador da extremidade esquerda 'End'. Em cada etapa, ele lê o símbolo na fita sob sua cabeça. Ele grava um novo símbolo na célula da fita e então move a cabeça para a esquerda ou para a direita. Uma função de transição determina as ações a serem tomadas.
Tem dois estados especiais chamados accept state e reject state. Se em qualquer ponto do tempo ele entrar no estado aceito, a entrada será aceita e se entrar no estado rejeitado, a entrada será rejeitada pelo TM. Em alguns casos, ele continua a funcionar infinitamente sem ser aceito ou rejeitado por alguns símbolos de entrada específicos.
Note - As máquinas de Turing com fita semi-infinita são equivalentes às máquinas de Turing padrão.
Um autômato linear limitado é uma máquina de Turing não determinística de múltiplas trilhas com uma fita de algum comprimento finito limitado.
Length = function (Length of the initial input string, constant c)
Aqui,
Memory information ≤ c × Input information
O cálculo é restrito à área constante limitada. O alfabeto de entrada contém dois símbolos especiais que servem como marcadores da extremidade esquerda e da extremidade direita, o que significa que as transições não se movem para a esquerda do marcador da extremidade esquerda nem para a direita do marcador da extremidade direita da fita.
Um autômato linear limitado pode ser definido como um 8-tupla (Q, X, ∑, q 0 , ML, MR, δ, F) onde -
Q é um conjunto finito de estados
X é o alfabeto da fita
∑ é o alfabeto de entrada
q0 é o estado inicial
ML é o marcador da extremidade esquerda
MRé o marcador da extremidade direita onde M R ≠ M L
δ é uma função de transição que mapeia cada par (estado, símbolo de fita) para (estado, símbolo de fita, Constante 'c') onde c pode ser 0 ou +1 ou -1
F é o conjunto de estados finais

Um autômato limitado linear determinístico é sempre context-sensitive e o autômato linear limitado com linguagem vazia é undecidable..
Uma linguagem é chamada Decidable ou Recursive se houver uma máquina de Turing que aceita e pára em cada string de entrada w. Cada linguagem decidível é Turing-Aceitável.

Um problema de decisão P é decidível se o idioma L de todas as instâncias sim para P é decidível.
Para uma linguagem decidível, para cada string de entrada, a TM para no estado de aceitação ou rejeição, conforme representado no diagrama a seguir -

Exemplo 1
Descubra se o seguinte problema é decidível ou não -
É um número 'm' primo?
Solução
Números primos = {2, 3, 5, 7, 11, 13, ………… ..}
Divida o número ‘m’ por todos os números entre '2' e '√m' começando em '2'.
Se algum desses números produzir um resto zero, ele vai para o “estado Rejeitado”, caso contrário, ele vai para o “estado Aceito”. Portanto, aqui a resposta pode ser 'Sim' ou 'Não'.
Hence, it is a decidable problem.
Exemplo 2
Dado um idioma regular L e corda w, como podemos verificar se w ∈ L?
Solução
Pegue o DFA que aceita L e verifique se w é aceito

Alguns problemas mais decidíveis são -
- O DFA aceita o idioma vazio?
- É L 1 ∩ L 2 = ∅ para conjuntos regulares?
Note -
Se um idioma L é decidível, então seu complemento L' também é decidível
Se um idioma é decidível, então há um enumerador para ele.
Para uma linguagem indecidível, não há Máquina de Turing que aceita a linguagem e toma uma decisão para cada string de entrada w(O TM pode tomar decisões para alguma string de entrada). Um problema de decisãoP é chamado de "indecidível" se o idioma L de todas as instâncias sim para Pnão é decidível. Linguagens indecidíveis não são linguagens recursivas, mas às vezes, podem ser linguagens enumeráveis recursivamente.

Exemplo
- O problema de parada da máquina de Turing
- O problema da mortalidade
- O problema da matriz mortal
- O problema de correspondência do Post, etc.
Input - Uma máquina de Turing e uma string de entrada w.
Problem - A máquina de Turing termina o cálculo da coluna wem um número finito de etapas? A resposta deve ser sim ou não.
Proof- A princípio, vamos supor que tal máquina de Turing existe para resolver esse problema e depois mostraremos que ela se contradiz. Chamaremos esta máquina de Turing como umHalting machineque produz um 'sim' ou 'não' em uma quantidade finita de tempo. Se a máquina de parada terminar em um período de tempo finito, a saída vem como 'sim', caso contrário, como 'não'. A seguir está o diagrama de blocos de uma máquina de parada -

Agora vamos projetar um inverted halting machine (HM)’ como -
E se H retorna SIM e, em seguida, faz um loop para sempre.
E se H retorna NÃO e depois pára.
A seguir está o diagrama de blocos de uma 'máquina de parada invertida' -

Além disso, uma máquina (HM)2 cuja entrada em si é construída da seguinte forma -
- Se (HM) 2 parar na entrada, loop para sempre.
- Senão, pare.
Aqui, temos uma contradição. Portanto, o problema da parada éundecidable.
O teorema de Rice afirma que qualquer propriedade semântica não trivial de uma linguagem que é reconhecida por uma máquina de Turing é indecidível. Uma propriedade, P, é a linguagem de todas as máquinas de Turing que satisfazem essa propriedade.
Definição formal
Se P for uma propriedade não trivial e a linguagem que detém a propriedade, L p , for reconhecida pela máquina de Turing M, então L p = {<M> | L (M) ∈ P} é indecidível.
Descrição e propriedades
A propriedade das linguagens, P, é simplesmente um conjunto de linguagens. Se alguma linguagem pertence a P (L ∈ P), diz-se que L satisfaz a propriedade P.
Uma propriedade é chamada de trivial se não for satisfeita por nenhuma linguagem recursivamente enumerável ou se for satisfeita por todas as linguagens recursivamente enumeráveis.
Uma propriedade não trivial é satisfeita por algumas linguagens recursivamente enumeráveis e não é satisfeita por outras. Falando formalmente, em uma propriedade não trivial, onde L ∈ P, ambas as seguintes propriedades são válidas:
Property 1 - Existem máquinas de Turing, M1 e M2 que reconhecem o mesmo idioma, ou seja (<M1>, <M2> ∈ L) ou (<M1>, <M2> ∉ L)
Property 2 - Existem máquinas de Turing M1 e M2, onde M1 reconhece o idioma enquanto M2 não, ou seja, <M1> ∈ L e <M2> ∉ L
Prova
Suponha que uma propriedade P não seja trivial e φ ∈ P.
Como P não é trivial, pelo menos uma linguagem satisfaz P, ou seja, L (M 0 ) ∈ P, ∋ Máquina de Turing M 0 .
Seja w uma entrada em um determinado instante e N é uma Máquina de Turing que segue -
Na entrada x
- Execute M em w
- Se M não aceitar (ou não parar), então não aceite x (ou não pare)
- Se M aceitar w, execute M 0 em x. Se M 0 aceita x, então aceite x.
Uma função que mapeia uma instância ATM = {<M, w> | M aceita a entrada w} para um N tal que
- Se M aceita w e N aceita a mesma linguagem que M 0 , então L (M) = L (M 0 ) ∈ p
- Se M não aceita w e N aceita φ, então L (N) = φ ∉ p
Visto que A TM é indecidível e pode ser reduzido a Lp, Lp também é indecidível.
O Post Correspondence Problem (PCP), introduzido por Emil Post em 1946, é um problema de decisão indecidível. O problema PCP sobre um alfabeto ∑ é declarado da seguinte forma -
Dadas as duas listas a seguir, M e N de strings não vazias em ∑ -
M = (x 1 , x 2 , x 3 , ………, x n )
N = (y 1 , y 2 , y 3 , ………, y n )
Podemos dizer que existe uma solução de pós-correspondência, se para algum i 1 , i 2 , ………… i k , onde 1 ≤ i j ≤ n, a condição x i1 …… .x ik = y i1 ……. y ik satisfaz.
Exemplo 1
Descubra se as listas
M = (abb, aa, aaa) e N = (bba, aaa, aa)
tem uma solução de correspondência postal?
Solução
| x 1 | x 2 | x 3 | |
|---|---|---|---|
| M | Abb | aa | aaa |
| N | Bba | aaa | aa |
Aqui,
x2x1x3 = ‘aaabbaaa’
e y2y1y3 = ‘aaabbaaa’
Nós podemos ver isso
x2x1x3 = y2y1y3
Portanto, a solução é i = 2, j = 1, and k = 3.
Exemplo 2
Descubra se as listas M = (ab, bab, bbaaa) e N = (a, ba, bab) tem uma solução de correspondência postal?
Solução
| x 1 | x 2 | x 3 | |
|---|---|---|---|
| M | ab | babinha | bbaaa |
| N | uma | BA | babinha |
Neste caso, não há solução porque -
| x2x1x3 | ≠ | y2y1y3 | (Os comprimentos não são iguais)
Portanto, pode-se dizer que este problema de pós-correspondência é undecidable.