Introdução à gramática livre de contexto

Definition - Uma gramática livre de contexto (CFG) que consiste em um conjunto finito de regras gramaticais é um quádruplo (N, T, P, S) Onde

N é um conjunto de símbolos não terminais.
T é um conjunto de terminais onde N ∩ T = NULL.
P é um conjunto de regras, P: N → (N ∪ T)*, ou seja, o lado esquerdo da regra de produção P tem qualquer contexto certo ou contexto esquerdo.
S é o símbolo inicial.

Example

A gramática ({A}, {a, b, c}, P, A), P: A → aA, A → abc.
A gramática ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
A gramática ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε

Geração de Árvore de Derivação

Uma árvore de derivação ou árvore de análise é uma árvore com raiz ordenada que representa graficamente as informações semânticas de uma string derivada de uma gramática livre de contexto.

Técnica de Representação

Root vertex - Deve ser identificado pelo símbolo de início.
Vertex - Rotulado por um símbolo não terminal.
Leaves - Identificado por um símbolo de terminal ou ε.

Se S → x ₁ x ₂ …… x _n é uma regra de produção em um CFG, então a árvore de análise / árvore de derivação será a seguinte -

Existem duas abordagens diferentes para desenhar uma árvore de derivação -

Top-down Approach −

Começa com o símbolo inicial S
Desce até as folhas das árvores usando produções

Bottom-up Approach −

Começa com folhas de árvore
Prossegue para cima até a raiz, que é o símbolo inicial S

Derivação ou produção de uma árvore

A derivação ou o rendimento de uma árvore de análise é a string final obtida pela concatenação dos rótulos das folhas da árvore da esquerda para a direita, ignorando os nulos. No entanto, se todas as folhas forem Nulas, a derivação será Nula.

Example

Seja um CFG {N, T, P, S}

N = {S}, T = {a, b}, símbolo inicial = S, P = S → SS | aSb | ε

Uma derivação do CFG acima é “abaabb”

S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Forma sentencial e árvore de derivação parcial

Uma árvore de derivação parcial é uma subárvore de uma árvore de derivação / árvore de análise de forma que todos os seus filhos estão na subárvore ou nenhum deles está na subárvore.

Example

Se em qualquer CFG as produções são -

S → AB, A → aaA | ε, B → Bb | ε

a árvore de derivação parcial pode ser a seguinte -

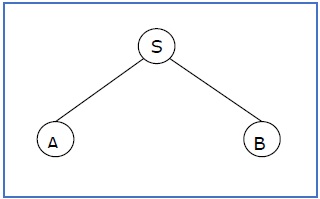
Se uma árvore de derivação parcial contém a raiz S, é chamada de sentential form. A subárvore acima também está em forma sentencial.

Derivação mais à esquerda e mais à direita de uma string

Leftmost derivation - A derivação mais à esquerda é obtida aplicando a produção à variável mais à esquerda em cada etapa.
Rightmost derivation - Uma derivação mais à direita é obtida aplicando a produção à variável mais à direita em cada etapa.

Example

Deixe qualquer conjunto de regras de produção em um CFG ser

X → X + X | X * X | X | uma

sobre um alfabeto {a}.

A derivação mais à esquerda para a string "a+a*a" pode ser -

X → X + X → a + X → a + X * X → a + a * X → a + a * a

A derivação gradual da string acima é mostrada abaixo -

A derivação mais à direita para a string acima "a+a*a" pode ser -

X → X * X → X * a → X + X * a → X + a * a → a + a * a

A derivação gradual da string acima é mostrada abaixo -

Gramáticas recursivas esquerda e direita

Em uma gramática livre de contexto G, se houver uma produção no formulário X → Xa Onde X é um não terminal e ‘a’ é uma cadeia de terminais, é chamada de left recursive production. A gramática com uma produção recursiva à esquerda é chamada deleft recursive grammar.

E se em uma gramática livre de contexto G, se houver uma produção está na forma X → aX Onde X é um não terminal e ‘a’ é uma cadeia de terminais, é chamada de right recursive production. A gramática com uma produção recursiva correta é chamada deright recursive grammar.