Noções básicas de computadores - sistema numérico
A técnica para representar e trabalhar com números é chamada number system. Decimal number systemé o sistema numérico mais comum. Outros sistemas de números populares incluem binary number system, octal number system, hexadecimal number system, etc.
Sistema de Número Decimal
O sistema de números decimais é um base 10sistema numérico com 10 dígitos de 0 a 9. Isso significa que qualquer quantidade numérica pode ser representada usando esses 10 dígitos. O sistema de números decimais também é umpositional value system. Isso significa que o valor dos dígitos dependerá de sua posição. Vamos dar um exemplo para entender isso.
Digamos que temos três números - 734, 971 e 207. O valor de 7 em todos os três números é diferente−
- Em 734, o valor de 7 é 7 centenas ou 700 ou 7 × 100 ou 7 × 10 2
- Em 971, o valor de 7 é 7 dezenas ou 70 ou 7 × 10 ou 7 × 10 1
- Em 207, o valor 0f 7 é 7 unidades ou 7 ou 7 × 1 ou 7 × 10 0
A ponderação de cada posição pode ser representada da seguinte forma -

Nos sistemas digitais, as instruções são dadas por meio de sinais elétricos; a variação é feita variando a tensão do sinal. É difícil ter 10 tensões diferentes para implementar o sistema de numeração decimal em equipamento digital. Assim, muitos sistemas numéricos que são mais fáceis de implementar digitalmente foram desenvolvidos. Vamos examiná-los em detalhes.
Sistema de número binário
A maneira mais fácil de variar as instruções por meio de sinais elétricos é o sistema de dois estados - ligado e desligado. On é representado como 1 e off como 0, embora 0 não seja realmente nenhum sinal, mas um sinal em uma tensão mais baixa. O sistema numérico que tem apenas estes dois dígitos - 0 e 1 - é chamadobinary number system.
Cada dígito binário também é chamado de bit. O sistema de números binários também é um sistema de valores posicionais, em que cada dígito tem um valor expresso em potências de 2, conforme exibido aqui.

Em qualquer número binário, o dígito mais à direita é chamado least significant bit (LSB) e o dígito mais à esquerda é chamado most significant bit (MSB).
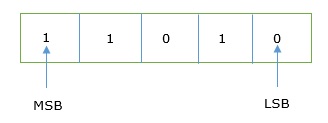
E o equivalente decimal desse número é a soma do produto de cada dígito com seu valor posicional.
11010 2 = 1 × 2 4 + 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0
= 16 + 8 + 0 + 2 + 0
= 26 10
A memória do computador é medida em termos de quantos bits ela pode armazenar. Aqui está um gráfico para a conversão da capacidade de memória.
- 1 byte (B) = 8 bits
- 1 kilobytes (KB) = 1.024 bytes
- 1 megabyte (MB) = 1024 KB
- 1 Gigabyte (GB) = 1024 MB
- 1 Terabyte (TB) = 1.024 GB
- 1 exabyte (EB) = 1024 PB
- 1 zetabyte = 1024 EB
- 1 Yottabyte (YB) = 1024 ZB
Sistema numérico octal
Octal number system tem oito dígitos - 0, 1, 2, 3, 4, 5, 6 e 7. O sistema numérico octal também é um sistema de valores posicionais em que cada dígito tem seu valor expresso em potências de 8, conforme mostrado aqui -

O equivalente decimal de qualquer número octal é a soma do produto de cada dígito com seu valor posicional.
726 8 = 7 × 8 2 + 2 × 8 1 + 6 × 8 0
= 448 + 16 + 6
= 470 10
Sistema numérico hexadecimal
Octal number system tem 16 símbolos - 0 a 9 e A a F onde A é igual a 10, B é igual a 11 e assim por diante até F. O sistema numérico hexadecimal também é um sistema de valores posicionais em que cada dígito tem seu valor expresso em potências de 16 , como mostrado aqui -

O equivalente decimal de qualquer número hexadecimal é a soma do produto de cada dígito com seu valor posicional.
27FB 16 = 2 × 16 3 + 7 × 16 2 + 15 × 16 1 + 10 × 16 0
= 8192 + 1792 + 240 +10
= 10234 10
Relação do sistema numérico
A tabela a seguir descreve a relação entre os sistemas numéricos decimais, binários, octal e hexadecimal.
| HEXADECIMAL | DECIMAL | OCTAL | BINÁRIO |
|---|---|---|---|
| 0 | 0 | 0 | 0000 |
| 1 | 1 | 1 | 0001 |
| 2 | 2 | 2 | 0010 |
| 3 | 3 | 3 | 0011 |
| 4 | 4 | 4 | 0100 |
| 5 | 5 | 5 | 0101 |
| 6 | 6 | 6 | 0110 |
| 7 | 7 | 7 | 0111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| UMA | 10 | 12 | 1010 |
| B | 11 | 13 | 1011 |
| C | 12 | 14 | 1100 |
| D | 13 | 15 | 1101 |
| E | 14 | 16 | 1110 |
| F | 15 | 17 | 1111 |
ASCII
Além dos dados numéricos, o computador deve ser capaz de lidar com alfabetos, sinais de pontuação, operadores matemáticos, símbolos especiais, etc. que formam o conjunto completo de caracteres do idioma inglês. O conjunto completo de caracteres ou símbolos são chamados de códigos alfanuméricos. O código alfanumérico completo normalmente inclui -
- 26 letras maiúsculas
- 26 letras minúsculas
- 10 dígitos
- 7 sinais de pontuação
- 20 a 40 caracteres especiais
Agora, um computador entende apenas valores numéricos, qualquer que seja o sistema numérico usado. Portanto, todos os caracteres devem ter um equivalente numérico chamado código alfanumérico. O código alfanumérico mais amplamente utilizado é o American Standard Code for Information Interchange (ASCII). ASCII é um código de 7 bits que possui 128 (27) códigos possíveis.

ISCII
ISCII significa Indian Script Code for Information Interchange. IISCII foi desenvolvido para oferecer suporte a idiomas indianos no computador. Os idiomas suportados pelo IISCI incluem Devanagari, Tamil, Bangla, Gujarati, Gurmukhi, Tamil, Telugu, etc. O IISCI é usado principalmente por departamentos governamentais e, antes que pudesse pegar, um novo padrão de codificação universal chamadoUnicode foi introduzido.
Unicode
Unicode é um sistema de codificação internacional projetado para ser usado com scripts de diferentes idiomas. Cada caractere ou símbolo é atribuído a um valor numérico exclusivo, em grande parte dentro da estrutura do ASCII. Anteriormente, cada script tinha seu próprio sistema de codificação, que poderia entrar em conflito uns com os outros.
Em contraste, isso é o que o Unicode oficialmente pretende fazer - o Unicode fornece um número exclusivo para cada caractere, não importa a plataforma, não importa o programa, não importa o idioma .