Projeto do compilador - análise de sintaxe

A análise de sintaxe ou análise sintática é a segunda fase de um compilador. Neste capítulo, aprenderemos os conceitos básicos usados na construção de um parser.

Vimos que um analisador léxico pode identificar tokens com a ajuda de expressões regulares e regras de padrão. Mas um analisador léxico não pode verificar a sintaxe de uma determinada frase devido às limitações das expressões regulares. Expressões regulares não podem verificar tokens de balanceamento, como parênteses. Portanto, esta fase usa gramática livre de contexto (CFG), que é reconhecida por autômatos push-down.

CFG, por outro lado, é um superconjunto da Gramática Regular, conforme ilustrado abaixo:

Isso implica que toda gramática regular também é livre de contexto, mas existem alguns problemas, que estão além do escopo da gramática regular. CFG é uma ferramenta útil para descrever a sintaxe das linguagens de programação.

Gramática Livre de Contexto

Nesta seção, veremos primeiro a definição de gramática livre de contexto e apresentaremos as terminologias usadas na tecnologia de análise.

Uma gramática livre de contexto tem quatro componentes:

Um conjunto de non-terminals(V). Não terminais são variáveis sintáticas que denotam conjuntos de strings. Os não terminais definem conjuntos de strings que ajudam a definir a linguagem gerada pela gramática.
Um conjunto de tokens, conhecido como terminal symbols(Σ). Terminais são os símbolos básicos a partir dos quais as strings são formadas.
Um conjunto de productions(P). As produções de uma gramática especificam a maneira pela qual os terminais e não terminais podem ser combinados para formar strings. Cada produção consiste em umnon-terminal chamado de lado esquerdo da produção, uma seta e uma sequência de tokens e / ou on- terminals, chamado de lado direito da produção.
Um dos não terminais é designado como o símbolo de início (S); de onde a produção começa.

As strings são derivadas do símbolo de início, substituindo repetidamente um não terminal (inicialmente o símbolo de início) pelo lado direito de uma produção, para esse não terminal.

Exemplo

Tomamos o problema da linguagem palíndromo, que não pode ser descrita por meio da Expressão Regular. Ou seja, L = {w | w = w ^R } não é uma linguagem regular. Mas pode ser descrito por meio do CFG, conforme ilustrado a seguir:

G = ( V, Σ, P, S )

Onde:

V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }

Esta gramática descreve a linguagem do palíndromo, como: 1001, 11100111, 00100, 1010101, 11111, etc.

Analisadores de sintaxe

Um analisador de sintaxe ou analisador obtém a entrada de um analisador léxico na forma de fluxos de token. O analisador analisa o código-fonte (fluxo de token) em relação às regras de produção para detectar quaisquer erros no código. A saída desta fase é umparse tree.

Dessa forma, o analisador realiza duas tarefas, ou seja, analisar o código, procurar erros e gerar uma árvore de análise como saída da fase.

Espera-se que os analisadores analisem todo o código, mesmo que existam alguns erros no programa. Analisadores usam estratégias de recuperação de erros, que aprenderemos mais tarde neste capítulo.

Derivação

Uma derivação é basicamente uma sequência de regras de produção, a fim de obter a string de entrada. Durante a análise, tomamos duas decisões para alguma forma sentencial de entrada:

Decidir o não terminal que deve ser substituído.
Decidir a regra de produção, pela qual, o não terminal será substituído.

Para decidir qual não terminal deve ser substituído pela regra de produção, podemos ter duas opções.

Derivação mais à esquerda

Se a forma sentencial de uma entrada for digitalizada e substituída da esquerda para a direita, é chamada de derivação mais à esquerda. A forma sentencial derivada da derivação mais à esquerda é chamada de forma sentencial à esquerda.

Derivação mais à direita

Se digitalizarmos e substituirmos a entrada por regras de produção, da direita para a esquerda, isso é conhecido como derivação da extrema direita. A forma sentencial derivada da derivação mais à direita é chamada de forma sentencial à direita.

Example

Regras de produção:

E → E + E
E → E * E
E → id

String de entrada: id + id * id

A derivação mais à esquerda é:

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

Observe que o não terminal mais à esquerda é sempre processado primeiro.

A derivação mais à direita é:

E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id

Analisar árvore

Uma árvore de análise é uma representação gráfica de uma derivação. É conveniente ver como as strings são derivadas do símbolo inicial. O símbolo inicial da derivação se torna a raiz da árvore de análise. Vamos ver isso por um exemplo do último tópico.

Tomamos a derivação mais à esquerda de a + b * c

A derivação mais à esquerda é:

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

Passo 1:

E → E * E

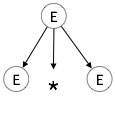
Passo 2:

E → E + E * E

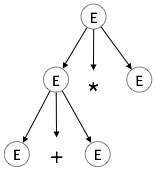
Etapa 3:

E → id + E * E

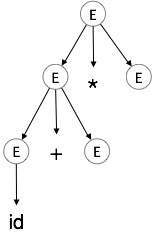
Passo 4:

E → id + id * E

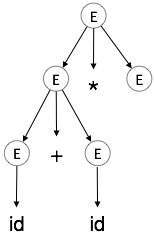
Etapa 5:

E → id + id * id

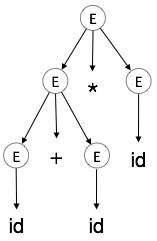
Em uma árvore de análise:

Todos os nós folha são terminais.
Todos os nós internos são não terminais.
O percurso em ordem fornece a string de entrada original.

Uma árvore de análise descreve associatividade e precedência de operadores. A subárvore mais profunda é percorrida primeiro, portanto, o operador dessa subárvore tem precedência sobre o operador que está nos nós pais.

Ambiguidade

Uma gramática G é considerada ambígua se tiver mais de uma árvore de análise (derivação esquerda ou direita) para pelo menos uma string.

Example

E → E + E
E → E – E
E → id

Para a string id + id - id, a gramática acima gera duas árvores de análise:

A linguagem gerada por uma gramática ambígua é considerada inherently ambiguous. A ambigüidade na gramática não é boa para a construção de um compilador. Nenhum método pode detectar e remover a ambigüidade automaticamente, mas pode ser removido reescrevendo toda a gramática sem ambigüidade ou definindo e seguindo as restrições de associatividade e precedência.

Associatividade

Se um operando tiver operadores em ambos os lados, o lado em que o operador assume esse operando é decidido pela associatividade desses operadores. Se a operação for associativa à esquerda, o operando será obtido pelo operador à esquerda ou, se a operação for associativa à direita, o operador à direita obterá o operando.

Example

Operações como adição, multiplicação, subtração e divisão são associativas à esquerda. Se a expressão contiver:

id op id op id

será avaliado como:

(id op id) op id

Por exemplo, (id + id) + id

Operações como exponenciação são associativas à direita, ou seja, a ordem de avaliação na mesma expressão será:

id op (id op id)

Por exemplo, id ^ (id ^ id)

Precedência

Se dois operadores diferentes compartilham um operando comum, a precedência dos operadores decide quem ficará com o operando. Ou seja, 2 + 3 * 4 pode ter duas árvores de análise sintática diferentes, uma correspondendo a (2 + 3) * 4 e outra correspondendo a 2+ (3 * 4). Ao definir a precedência entre os operadores, esse problema pode ser facilmente removido. Como no exemplo anterior, matematicamente * (multiplicação) tem precedência sobre + (adição), então a expressão 2 + 3 * 4 sempre será interpretada como:

2 + (3 * 4)

Esses métodos diminuem as chances de ambigüidade em um idioma ou em sua gramática.

Recursão à esquerda

Uma gramática se torna recursiva à esquerda se tiver qualquer 'A' não terminal cuja derivação contém o próprio 'A' como o símbolo mais à esquerda. A gramática recursiva à esquerda é considerada uma situação problemática para analisadores top-down. Os analisadores de cima para baixo começam a analisar a partir do símbolo Iniciar, que em si não é terminal. Portanto, quando o analisador encontra o mesmo não terminal em sua derivação, torna-se difícil para ele julgar quando parar de analisar o não terminal esquerdo e ele entra em um loop infinito.

Example:

(1) A => Aα | β

(2) S => Aα | β 
    A => Sd

(1) é um exemplo de recursão imediata à esquerda, onde A é qualquer símbolo não terminal e α representa uma sequência de não terminais.

(2) é um exemplo de recursão indireta à esquerda.

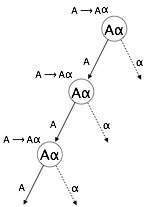
Um analisador de cima para baixo primeiro analisará o A, que por sua vez produzirá uma string que consiste no próprio A e o analisador pode entrar em um loop para sempre.

Remoção de recursão à esquerda

Uma maneira de remover a recursão à esquerda é usar a seguinte técnica:

A produção

A => Aα | β

é convertido nas seguintes produções

A => βA'
A'=> αA' | ε

Isso não afeta as cadeias de caracteres derivadas da gramática, mas remove a recursão à esquerda imediata.

O segundo método é usar o algoritmo a seguir, que deve eliminar todas as recursões diretas e indiretas à esquerda.

START

Arrange non-terminals in some order like A1, A2, A3,…, A_n

   for each i from 1 to n
      {
      for each j from 1 to i-1
         {
         replace each production of form A_i ⟹Aj
         with A_i ⟹ δ1  | δ2 | δ3 |…|  
         where A_j ⟹ δ₁ | δ₂|…| δ_n  are current A_j productions
         }
      }
   eliminate immediate left-recursion
   
END

Example

O conjunto de produção

S => Aα | β 
A => Sd

depois de aplicar o algoritmo acima, deve se tornar

S => Aα | β 
A => Aαd | βd

e, em seguida, remova a recursão à esquerda imediata usando a primeira técnica.

A  => βdA'
A' => αdA' | ε

Agora, nenhuma parte da produção tem recursão à esquerda direta ou indireta.

Fatoração à esquerda

Se mais de uma regra de produção de gramática tiver uma string de prefixo comum, o analisador de cima para baixo não poderá fazer uma escolha sobre qual produção deve ser realizada para analisar a string em questão.

Example

Se um analisador top-down encontra uma produção como

A ⟹ αβ | α | …

Então, ele não pode determinar qual produção seguir para analisar a string, já que ambas as produções estão iniciando no mesmo terminal (ou não). Para remover essa confusão, usamos uma técnica chamada fatoração à esquerda.

A fatoração à esquerda transforma a gramática para torná-la útil para analisadores de cima para baixo. Nesta técnica, fazemos uma produção para cada prefixo comum e o resto da derivação é adicionado por novas produções.

Example

As produções acima podem ser escritas como

A => αA'
A'=> β |  | …

Agora, o analisador tem apenas uma produção por prefixo, o que torna mais fácil tomar decisões.

Conjuntos de primeiros e seguintes

Uma parte importante da construção da tabela do analisador é criar primeiro e seguir os conjuntos. Esses conjuntos podem fornecer a posição real de qualquer terminal na derivação. Isso é feito para criar a tabela de análise em que a decisão de substituir T [A, t] = α por alguma regra de produção.

Primeiro set

Este conjunto é criado para saber qual símbolo terminal é derivado na primeira posição por um não terminal. Por exemplo,

α → t β

Ou seja, α deriva t (terminal) na primeira posição. Portanto, t ∈ PRIMEIRO (α).

Algoritmo para calcular o primeiro conjunto

Observe a definição do conjunto FIRST (α):

se α for um terminal, então FIRST (α) = {α}.
se α é um não terminal e α → ℇ é uma produção, então FIRST (α) = {ℇ}.
se α é um não terminal e α → 1 2 3… n e qualquer FIRST () contém t então t está em FIRST (α).

O primeiro conjunto pode ser visto como:

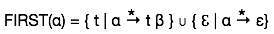
Seguir Set

Da mesma forma, calculamos qual símbolo terminal segue imediatamente um α não terminal nas regras de produção. Não consideramos o que o não-terminal pode gerar, mas, em vez disso, vemos qual seria o próximo símbolo do terminal que segue as produções de um não-terminal.

Algoritmo para calcular o conjunto de acompanhamento:

se α é um símbolo de início, então FOLLOW () = $
se α é um não terminal e tem uma produção α → AB, então FIRST (B) está em FOLLOW (A) exceto ℇ.
se α é um não terminal e tem uma produção α → AB, onde B ℇ, então FOLLOW (A) está em FOLLOW (α).

O conjunto seguinte pode ser visto como: FOLLOW (α) = {t | S * αt *}

Limitações dos analisadores de sintaxe

Os analisadores de sintaxe recebem suas entradas, na forma de tokens, de analisadores lexicais. Os analisadores lexicais são responsáveis pela validade de um token fornecido pelo analisador de sintaxe. Os analisadores de sintaxe têm as seguintes desvantagens -

não pode determinar se um token é válido,
ele não pode determinar se um token é declarado antes de ser usado,
ele não pode determinar se um token foi inicializado antes de ser usado,
ele não pode determinar se uma operação executada em um tipo de token é válida ou não.

Essas tarefas são realizadas pelo analisador semântico, que estudaremos na Análise Semântica.