Criptografia de chave pública

Ao contrário da criptografia de chave simétrica, não encontramos o uso histórico da criptografia de chave pública. É um conceito relativamente novo.

A criptografia simétrica era adequada para organizações como governos, forças armadas e grandes corporações financeiras que estavam envolvidas na comunicação confidencial.

Com a disseminação de redes de computadores menos seguras nas últimas décadas, sentiu-se uma necessidade genuína de usar criptografia em maior escala. A chave simétrica foi considerada não prática devido aos desafios enfrentados para o gerenciamento de chaves. Isso deu origem aos criptosistemas de chave pública.

O processo de criptografia e descriptografia é descrito na ilustração a seguir -

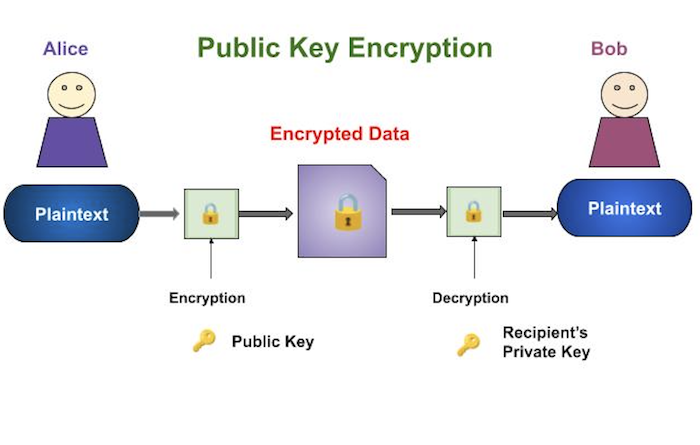
As propriedades mais importantes do esquema de criptografia de chave pública são -

Chaves diferentes são usadas para criptografar e descriptografar. Esta é uma propriedade que define este esquema diferente do esquema de criptografia simétrica.
Cada receptor possui uma chave de descriptografia exclusiva, geralmente conhecida como sua chave privada.
O receptor precisa publicar uma chave de criptografia, conhecida como sua chave pública.
Alguma garantia da autenticidade de uma chave pública é necessária neste esquema para evitar falsificação pelo adversário como o receptor. Geralmente, este tipo de criptosistema envolve terceiros confiáveis que certificam que uma determinada chave pública pertence apenas a uma pessoa ou entidade específica.
O algoritmo de criptografia é complexo o suficiente para proibir o invasor de deduzir o texto simples do texto cifrado e a chave de criptografia (pública).
Embora as chaves privadas e públicas estejam relacionadas matematicamente, não é possível calcular a chave privada a partir da chave pública. Na verdade, a parte inteligente de qualquer criptosistema de chave pública consiste em projetar um relacionamento entre duas chaves.

Existem três tipos de esquemas de criptografia de chave pública. Nós os discutiremos nas seções a seguir -

RSA Cryptosystem

Este criptosistema é o sistema inicial. Continua a ser o criptossistema mais utilizado até hoje. O sistema foi inventado por três estudiososRon Rivest, Adi Shamir, e Len Adleman e, portanto, é denominado como criptosistema RSA.

Veremos dois aspectos do criptosistema RSA, primeiro a geração do par de chaves e segundo os algoritmos de criptografia-descriptografia.

Geração de par de chaves RSA

Cada pessoa ou parte que deseja participar na comunicação por meio de criptografia precisa gerar um par de chaves, a saber, a chave pública e a chave privada. O processo seguido na geração das chaves é descrito abaixo -

Generate the RSA modulus (n)
- Selecione dois primos grandes, pe q.
- Calcule n = p * q. Para criptografia forte e inquebrável, seja n um número grande, normalmente um mínimo de 512 bits.
Find Derived Number (e)
- Número e deve ser maior que 1 e menor que (p - 1) (q - 1).
- Não deve haver nenhum fator comum para e e (p - 1) (q - 1) exceto para 1. Em outras palavras, dois números e e (p - 1) (q - 1) são coprimos.
Form the public key
- O par de números (n, e) forma a chave pública RSA e é tornado público.
- Curiosamente, embora n seja parte da chave pública, a dificuldade em fatorar um grande número primo garante que o invasor não possa encontrar em tempo finito os dois primos (p & q) usados para obter n. Essa é a força da RSA.
Generate the private key
- A chave privada d é calculada de p, q e e. Para dados n e e, existe um número único d.
- O número d é o inverso do módulo e (p - 1) (q - 1). Isso significa que d é o número menor que (p - 1) (q - 1) tal que, quando multiplicado por e, é igual a 1 módulo (p - 1) (q - 1).
- Esta relação é escrita matematicamente da seguinte forma -

ed = 1 mod (p − 1)(q − 1)

O Algoritmo Euclidiano Estendido usa p, q e e como entrada e fornece d como saída.

Exemplo

Um exemplo de geração de par de chaves RSA é fornecido abaixo. (Para facilitar o entendimento, os primos p & q considerados aqui são valores pequenos. Praticamente, esses valores são muito altos).

Sejam dois primos p = 7 e q = 13. Assim, módulo n = pq = 7 x 13 = 91.
Selecione e = 5, que é uma escolha válida, uma vez que não há número que seja o fator comum de 5 e (p - 1) (q - 1) = 6 × 12 = 72, exceto para 1.
O par de números (n, e) = (91, 5) forma a chave pública e pode ser disponibilizado para qualquer pessoa a quem desejemos que nos envie mensagens criptografadas.
Insira p = 7, q = 13 e e = 5 para o Algoritmo Euclidiano Estendido. A saída será d = 29.
Verifique se o d calculado está correto calculando -

de = 29 × 5 = 145 = 1 mod 72

Portanto, a chave pública é (91, 5) e as chaves privadas é (91, 29).

Criptografia e descriptografia

Uma vez que o par de chaves tenha sido gerado, o processo de criptografia e descriptografia é relativamente simples e computacionalmente fácil.

Curiosamente, o RSA não opera diretamente em cadeias de bits como no caso da criptografia de chave simétrica. Ele opera em números módulo n. Portanto, é necessário representar o texto simples como uma série de números menores que n.

Criptografia RSA

Suponha que o remetente deseje enviar alguma mensagem de texto para alguém cuja chave pública seja (n, e).
O remetente então representa o texto simples como uma série de números menores que n.
Para criptografar o primeiro texto simples P, que é um número módulo n. O processo de criptografia é uma etapa matemática simples como -

C = P^e mod n

Em outras palavras, o texto cifrado C é igual ao texto simples P multiplicado por ele mesmo e vezes e então reduzido módulo n. Isso significa que C também é um número menor que n.
Voltando ao nosso exemplo de Geração de chave com texto simples P = 10, obtemos o texto cifrado C -

C = 10⁵ mod 91

RSA Decryption

O processo de descriptografia para RSA também é muito simples. Suponha que o receptor do par de chaves públicas (n, e) tenha recebido um texto cifrado C.
O receptor eleva C à potência de sua chave privada d. O resultado módulo n será o texto simples P.

Plaintext = C^d mod n

Voltando novamente ao nosso exemplo numérico, o texto cifrado C = 82 seria descriptografado para o número 10 usando a chave privada 29 -

Plaintext = 82²⁹ mod 91 = 10

Análise RSA

A segurança do RSA depende da força de duas funções distintas. O criptossistema RSA é o mais popular do sistema de criptografia de chave pública, que se baseia na dificuldade prática de fatorar números muito grandes.

Encryption Function - É considerada uma função unilateral de conversão de texto simples em texto cifrado e só pode ser revertida com o conhecimento da chave privada d.
Key Generation- A dificuldade de determinar uma chave privada de uma chave pública RSA é equivalente a fatorar o módulo n. Portanto, um invasor não pode usar o conhecimento de uma chave pública RSA para determinar uma chave privada RSA, a menos que possa fatorar n. É também uma função unilateral, ir dos valores p & q para o módulo n é fácil, mas o reverso não é possível.

Se alguma dessas duas funções for comprovada como não unilateral, o RSA será interrompido. De fato, se uma técnica de fatoração eficiente for desenvolvida, o RSA não será mais seguro.

A força da criptografia RSA diminui drasticamente contra ataques se os números peq não forem primos grandes e / ou a chave pública e escolhida for um número pequeno.

ElGamal Cryptosystem

Junto com o RSA, existem outros criptossistemas de chave pública propostos. Muitos deles são baseados em diferentes versões do Problema do Logaritmo Discreto.

O criptosistema ElGamal, denominado Variante da Curva Elíptica, é baseado no Problema do Logaritmo Discreto. Ele deriva a força da suposição de que os logaritmos discretos não podem ser encontrados em um período de tempo prático para um determinado número, enquanto a operação inversa da potência pode ser calculada com eficiência.

Vamos examinar uma versão simples do ElGamal que funciona com números módulo p. No caso das variantes da curva elíptica, é baseado em sistemas numéricos bastante diferentes.

Geração do par de chaves ElGamal

Cada usuário do criptossistema ElGamal gera o par de chaves da seguinte forma -

Choosing a large prime p. Geralmente, um número primo de comprimento de 1024 a 2048 bits é escolhido.
Choosing a generator element g.
- Esse número deve estar entre 1 e p - 1, mas não pode ser qualquer número.
- É um gerador do grupo multiplicativo de inteiros módulo p. Isso significa que para cada inteiro m co-primo a p, há um inteiro k tal que g ^k = a mod n.
  
  Por exemplo, 3 é gerador do grupo 5 (Z ₅ = {1, 2, 3, 4}).

N	3 ⁿ	3 ⁿ mod 5
1	3	3
2	9	4
3	27	2
4	81	1

Choosing the private key. A chave privada x é qualquer número maior que 1 e menor que p − 1.
Computing part of the public key. O valor y é calculado a partir dos parâmetros p, ge da chave privada x da seguinte forma -

y = g^x mod p

Obtaining Public key. A chave pública ElGamal consiste em três parâmetros (p, g, y).

Por exemplo, suponha que p = 17 e que g = 6 (pode-se confirmar que 6 é um gerador do grupo Z ₁₇ ). A chave privada x pode ser qualquer número maior que 1 e menor que 71, então escolhemos x = 5. O valor y é então calculado da seguinte maneira -

y = 6⁵ mod 17 = 7

Assim, a chave privada é 62 e a chave pública é (17, 6, 7).

Criptografia e descriptografia

A geração de um par de chaves ElGamal é comparativamente mais simples do que o processo equivalente para RSA. Mas a criptografia e a descriptografia são um pouco mais complexas do que RSA.

Criptografia ElGamal

Suponha que o remetente deseja enviar um texto simples para alguém cuja chave pública ElGamal é (p, g, y), então -

Sender representa o texto simples como uma série de números módulo p.
Para criptografar o primeiro texto simples P, que é representado como um número módulo p. O processo de criptografia para obter o texto cifrado C é o seguinte -
- Gere aleatoriamente um número k;
- Calcule dois valores C1 e C2, onde -

C1 = g^k mod p
C2 = (P^*y^k) mod p

Envie o texto cifrado C, consistindo em dois valores separados (C1, C2), enviados juntos.
Referindo-se ao nosso exemplo de geração de chave ElGamal dado acima, o texto simples P = 13 é criptografado da seguinte forma -
- Gere aleatoriamente um número, digamos k = 10
- Calcule os dois valores C1 e C2, onde -

C1 = 6¹⁰ mod 17
C2 = (13^*7¹⁰) mod 17 = 9

Envie o texto cifrado C = (C1, C2) = (15, 9).

ElGamal Decryption

Para descriptografar o texto cifrado (C1, C2) usando a chave privada x, as duas etapas a seguir são executadas -
- Calcule o inverso modular de (C1) ^x módulo p, que é (C1) ^-x , geralmente referido como fator de descriptografia.
- Obtenha o texto simples usando a seguinte fórmula -

C2 × (C1)^-x mod p = Plaintext

Em nosso exemplo, para descriptografar o texto cifrado C = (C1, C2) = (15, 9) usando a chave privada x = 5, o fator de descriptografia é

15^-5 mod 17 = 9

Extraia o texto simples P = (9 × 9) mod 17 = 13.

Análise ElGamal

No sistema ElGamal, cada usuário possui uma chave privada x. e temthree components de chave pública - prime modulus p, generator g, and public Y = g^x mod p. A força do ElGamal é baseada na dificuldade do problema de logaritmo discreto.

O tamanho da chave segura é geralmente> 1024 bits. Hoje, até chaves de 2048 bits são usadas. No que diz respeito à velocidade de processamento, o Elgamal é bastante lento, sendo usado principalmente para protocolos de autenticação de chaves. Devido à maior eficiência de processamento, as variantes da curva elíptica do ElGamal estão se tornando cada vez mais populares.

Criptografia de curva elíptica (ECC)

Criptografia de curva elíptica (ECC) é um termo usado para descrever um conjunto de ferramentas e protocolos criptográficos cuja segurança é baseada em versões especiais do problema de logaritmo discreto. Ele não usa números módulo p.

ECC é baseado em conjuntos de números que estão associados a objetos matemáticos chamados curvas elípticas. Existem regras para somar e calcular múltiplos desses números, assim como existem para os números módulo p.

ECC inclui variantes de muitos esquemas criptográficos que foram inicialmente projetados para números modulares, como criptografia ElGamal e Algoritmo de Assinatura Digital.

Acredita-se que o problema do logaritmo discreto seja muito mais difícil quando aplicado a pontos em uma curva elíptica. Isso solicita a mudança de números módulo p para pontos em uma curva elíptica. Além disso, um nível de segurança equivalente pode ser obtido com chaves mais curtas se usarmos variantes baseadas em curvas elípticas.

As chaves mais curtas resultam em dois benefícios -

Facilidade de gerenciamento de chaves
Computação eficiente

Esses benefícios tornam as variantes do esquema de criptografia baseadas em curvas elípticas altamente atraentes para aplicativos onde os recursos de computação são limitados.

Esquemas RSA e ElGamal - Uma Comparação

Vamos comparar brevemente os esquemas RSA e ElGamal nos vários aspectos.

RSA	ElGamal
É mais eficiente para criptografia.	É mais eficiente para descriptografar.
É menos eficiente para descriptografar.	É mais eficiente para descriptografar.
Para um determinado nível de segurança, chaves longas são necessárias no RSA.	Para o mesmo nível de segurança, são necessárias chaves muito curtas.
É amplamente aceito e usado.	É novo e não muito popular no mercado.