Estruturas de dados e algoritmos - Arrays

Array é um contêiner que pode conter um número fixo de itens e esses itens devem ser do mesmo tipo. A maioria das estruturas de dados faz uso de arrays para implementar seus algoritmos. A seguir estão os termos importantes para entender o conceito de Array.

Element - Cada item armazenado em uma matriz é chamado de elemento.
Index - Cada localização de um elemento em uma matriz possui um índice numérico, que é usado para identificar o elemento.

Representação de Matriz

Os arrays podem ser declarados de várias maneiras em diferentes idiomas. Para ilustração, vamos tomar a declaração do array C.

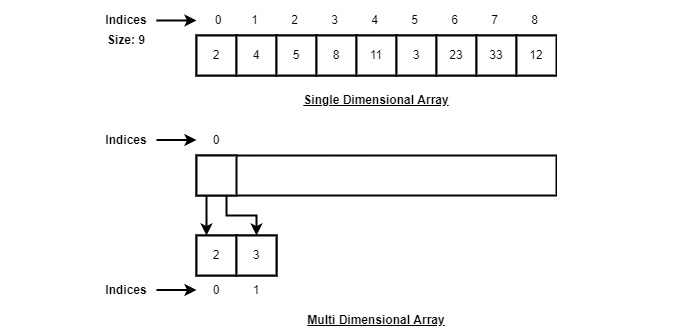
Conforme a ilustração acima, a seguir estão os pontos importantes a serem considerados.

O índice começa com 0.
O comprimento do array é 10, o que significa que ele pode armazenar 10 elementos.
Cada elemento pode ser acessado por meio de seu índice. Por exemplo, podemos buscar um elemento no índice 6 como 9.

Operações básicas

A seguir estão as operações básicas suportadas por uma matriz.

Traverse - imprime todos os elementos do array um por um.
Insertion - Adiciona um elemento no índice fornecido.
Deletion - Exclui um elemento no índice fornecido.
Search - Pesquisa um elemento usando o índice fornecido ou pelo valor.
Update - Atualiza um elemento no índice fornecido.

Em C, quando um array é inicializado com size, ele atribui valores padrão a seus elementos na seguinte ordem.

Tipo de dados	Valor padrão
bool	falso
Caracteres	0
int	0
flutuador	0,0
em dobro	0.0f
vazio
wchar_t	0

Operação transversal

Esta operação consiste em percorrer os elementos de uma matriz.

Exemplo

O programa a seguir percorre e imprime os elementos de uma matriz:

#include <stdio.h>
main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;   
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Quando compilamos e executamos o programa acima, ele produz o seguinte resultado -

Resultado

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8

Operação de Inserção

A operação de inserção é inserir um ou mais elementos de dados em uma matriz. Com base no requisito, um novo elemento pode ser adicionado no início, no final ou em qualquer índice da matriz.

Aqui, vemos uma implementação prática da operação de inserção, onde adicionamos dados no final da matriz -

Exemplo

A seguir está a implementação do algoritmo acima -

#include <stdio.h>

main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   
   printf("The original array elements are :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }

   n = n + 1;
	
   while( j >= k) {
      LA[j+1] = LA[j];
      j = j - 1;
   }

   LA[k] = item;

   printf("The array elements after insertion :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Quando compilamos e executamos o programa acima, ele produz o seguinte resultado -

Resultado

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after insertion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 10 
LA[4] = 7 
LA[5] = 8

Para outras variações da operação de inserção de matriz, clique aqui

Operação de Exclusão

A exclusão se refere à remoção de um elemento existente do array e à reorganização de todos os elementos de um array.

Algoritmo

Considerar LA é uma matriz linear com N elementos e K é um número inteiro positivo tal que K<=N. A seguir está o algoritmo para excluir um elemento disponível na K- ^ésima posição de LA.

1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA[J + 1]
5. Set J = J+1
6. Set N = N-1
7. Stop

Exemplo

A seguir está a implementação do algoritmo acima -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   j = k;
	
   while( j < n) {
      LA[j-1] = LA[j];
      j = j + 1;
   }
	
   n = n -1;
   
   printf("The array elements after deletion :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Quando compilamos e executamos o programa acima, ele produz o seguinte resultado -

Resultado

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after deletion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 7 
LA[3] = 8

Operação de Pesquisa

Você pode realizar uma pesquisa por um elemento da matriz com base em seu valor ou índice.

Algoritmo

Considerar LA é uma matriz linear com N elementos e K é um número inteiro positivo tal que K<=N. A seguir está o algoritmo para encontrar um elemento com um valor de ITEM usando a pesquisa sequencial.

1. Start
2. Set J = 0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop

Exemplo

A seguir está a implementação do algoritmo acima -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0, j = 0;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   while( j < n){
      if( LA[j] == item ) {
         break;
      }
		
      j = j + 1;
   }
	
   printf("Found element %d at position %d\n", item, j+1);
}

Quando compilamos e executamos o programa acima, ele produz o seguinte resultado -

Resultado

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
Found element 5 at position 3

Operação de atualização

A operação de atualização refere-se à atualização de um elemento existente da matriz em um determinado índice.

Algoritmo

Considerar LA é uma matriz linear com N elementos e K é um número inteiro positivo tal que K<=N. A seguir está o algoritmo para atualizar um elemento disponível na K- ^ésima posição de LA.

1. Start
2. Set LA[K-1] = ITEM
3. Stop

Exemplo

A seguir está a implementação do algoritmo acima -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5, item = 10;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   LA[k-1] = item;

   printf("The array elements after updation :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Quando compilamos e executamos o programa acima, ele produz o seguinte resultado -

Resultado

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after updation :
LA[0] = 1 
LA[1] = 3 
LA[2] = 10 
LA[3] = 7 
LA[4] = 8