Estruturas de dados e algoritmos - Guia rápido

Estrutura de dados é uma forma sistemática de organizar os dados para usá-los com eficiência. Os termos a seguir são os termos básicos de uma estrutura de dados.

Interface- Cada estrutura de dados possui uma interface. Interface representa o conjunto de operações que uma estrutura de dados suporta. Uma interface fornece apenas a lista de operações suportadas, tipo de parâmetros que eles podem aceitar e tipo de retorno dessas operações.
Implementation- A implementação fornece a representação interna de uma estrutura de dados. A implementação também fornece a definição dos algoritmos usados nas operações da estrutura de dados.

Características de uma estrutura de dados

Correctness - A implementação da estrutura de dados deve implementar sua interface corretamente.
Time Complexity - O tempo de execução ou o tempo de execução das operações da estrutura de dados deve ser o menor possível.
Space Complexity - O uso de memória de uma operação de estrutura de dados deve ser o mínimo possível.

Necessidade de estrutura de dados

Como os aplicativos estão ficando complexos e ricos em dados, existem três problemas comuns que os aplicativos enfrentam hoje em dia.

Data Search- Considere um estoque de 1 milhão (10 ⁶ ) itens de uma loja. Se o aplicativo for para pesquisar um item, ele deve pesquisar um item em 1 milhão (10 ⁶ ) itens toda vez, tornando a pesquisa mais lenta. Conforme os dados aumentam, a pesquisa se torna mais lenta.
Processor speed - A velocidade do processador embora seja muito alta, cai limitada se os dados crescerem para bilhões de registros.
Multiple requests - Como milhares de usuários podem pesquisar dados simultaneamente em um servidor web, até mesmo o servidor rápido falha ao pesquisar os dados.

Para resolver os problemas mencionados acima, as estruturas de dados vêm para resgatar. Os dados podem ser organizados em uma estrutura de dados de forma que não seja necessário pesquisar todos os itens, e os dados necessários podem ser pesquisados quase instantaneamente.

Casos de tempo de execução

Existem três casos que geralmente são usados para comparar o tempo de execução de várias estruturas de dados de maneira relativa.

Worst Case- Este é o cenário em que uma operação de estrutura de dados específica leva o tempo máximo que pode levar. Se o pior caso de uma operação for ƒ (n), então esta operação não levará mais do que ƒ (n) tempo, onde ƒ (n) representa a função de n.
Average Case- Este é o cenário que descreve o tempo médio de execução de uma operação de uma estrutura de dados. Se uma operação levar ƒ (n) tempo para ser executada, então m operações levarão mƒ (n) tempo.
Best Case- Este é o cenário que representa o menor tempo de execução possível de uma operação de uma estrutura de dados. Se uma operação levar tempo ƒ (n) para ser executada, então a operação real pode levar tempo como o número aleatório que seria máximo como ƒ (n).

Terminologia Básica

Data - Os dados são valores ou conjunto de valores.
Data Item - O item de dados refere-se a uma única unidade de valores.
Group Items - Os itens de dados divididos em subitens são chamados de itens de grupo.
Elementary Items - Os itens de dados que não podem ser divididos são chamados de itens elementares.
Attribute and Entity - Uma entidade é aquela que contém certos atributos ou propriedades, aos quais podem ser atribuídos valores.
Entity Set - Entidades de atributos semelhantes formam um conjunto de entidades.
Field - O campo é uma única unidade elementar de informação que representa um atributo de uma entidade.
Record - Registro é uma coleção de valores de campo de uma determinada entidade.
File - Arquivo é uma coleção de registros das entidades em um determinado conjunto de entidades.

Experimente a opção online

Você realmente não precisa configurar seu próprio ambiente para começar a aprender a linguagem de programação C. O Reason é muito simples, já configuramos o ambiente de Programação C online, para que você possa compilar e executar todos os exemplos disponíveis online ao mesmo tempo, enquanto faz seu trabalho teórico. Isso lhe dá confiança no que está lendo e para verificar o resultado com diferentes opções. Sinta-se à vontade para modificar qualquer exemplo e executá-lo online.

Experimente o seguinte exemplo usando o Try it opção disponível no canto superior direito da caixa do código de amostra -

#include <stdio.h>
int main(){
   /* My first program in C */
   printf("Hello, World! \n");
   return 0;
}

Para a maioria dos exemplos fornecidos neste tutorial, você encontrará a opção Experimente, portanto, faça uso dela e aproveite seu aprendizado.

Configuração de ambiente local

Se você ainda deseja configurar seu ambiente para a linguagem de programação C, você precisa das duas ferramentas a seguir disponíveis em seu computador: (a) Editor de Texto e (b) Compilador C.

Editor de texto

Isso será usado para digitar seu programa. Exemplos de poucos editores incluem o bloco de notas do Windows, o comando Editar do sistema operacional, Brief, Epsilon, EMACS e vim ou vi.

O nome e a versão do editor de texto podem variar em diferentes sistemas operacionais. Por exemplo, o Bloco de notas será usado no Windows e o vim ou vi pode ser usado no Windows, bem como no Linux ou UNIX.

Os arquivos que você cria com seu editor são chamados de arquivos-fonte e contêm o código-fonte do programa. Os arquivos de origem para programas C são normalmente nomeados com a extensão ".c"

Antes de iniciar sua programação, certifique-se de ter um editor de texto instalado e de ter experiência suficiente para escrever um programa de computador, salvá-lo em um arquivo, compilá-lo e finalmente executá-lo.

O compilador C

O código-fonte escrito no arquivo-fonte é a fonte legível para o seu programa. Ele precisa ser "compilado" para se transformar em linguagem de máquina para que sua CPU possa realmente executar o programa de acordo com as instruções fornecidas.

Este compilador de linguagem de programação C será usado para compilar seu código-fonte em um programa executável final. Presumimos que você tenha o conhecimento básico sobre um compilador de linguagem de programação.

O compilador mais frequentemente usado e disponível gratuitamente é o compilador GNU C / C ++. Caso contrário, você pode ter compiladores da HP ou Solaris se tiver os respectivos sistemas operacionais (SO).

A seção a seguir o orienta sobre como instalar o compilador GNU C / C ++ em vários sistemas operacionais. Estamos mencionando C / C ++ juntos porque o compilador GNU GCC funciona para as linguagens de programação C e C ++.

Instalação em UNIX / Linux

Se você estiver usando Linux or UNIXe, em seguida, verifique se o GCC está instalado em seu sistema digitando o seguinte comando na linha de comando -

$ gcc -v

Se você tiver um compilador GNU instalado em sua máquina, ele deve imprimir uma mensagem como a seguinte -

Using built-in specs.
Target: i386-redhat-linux
Configured with: ../configure --prefix = /usr .......
Thread model: posix
gcc version 4.1.2 20080704 (Red Hat 4.1.2-46)

Se o GCC não estiver instalado, você terá que instalá-lo usando as instruções detalhadas disponíveis em https://gcc.gnu.org/install/

Este tutorial foi escrito com base no Linux e todos os exemplos dados foram compilados no tipo Cent OS do sistema Linux.

Instalação em Mac OS

Se você usa Mac OS X, a maneira mais fácil de obter o GCC é baixar o ambiente de desenvolvimento Xcode do site da Apple e seguir as instruções simples de instalação. Depois de configurar o Xcode, você poderá usar o compilador GNU para C / C ++.

O Xcode está disponível atualmente em developer.apple.com/technologies/tools/

Instalação em Windows

Para instalar o GCC no Windows, você precisa instalar o MinGW. Para instalar o MinGW, vá para a página inicial do MinGW, www.mingw.org , e siga o link para a página de download do MinGW. Baixe a versão mais recente do programa de instalação do MinGW, que deve se chamar MinGW- <versão> .exe.

Ao instalar o MinWG, no mínimo, você deve instalar gcc-core, gcc-g ++, binutils e o tempo de execução do MinGW, mas você pode desejar instalar mais.

Adicione o subdiretório bin da instalação do MinGW ao seu PATH variável de ambiente, para que você possa especificar essas ferramentas na linha de comando por seus nomes simples.

Quando a instalação for concluída, você poderá executar gcc, g ++, ar, ranlib, dlltool e várias outras ferramentas GNU a partir da linha de comando do Windows.

Algoritmo é um procedimento passo a passo, que define um conjunto de instruções a serem executadas em uma determinada ordem para obter a saída desejada. Os algoritmos são geralmente criados independentemente das linguagens subjacentes, ou seja, um algoritmo pode ser implementado em mais de uma linguagem de programação.

Do ponto de vista da estrutura de dados, a seguir estão algumas categorias importantes de algoritmos -

Search - Algoritmo para pesquisar um item em uma estrutura de dados.
Sort - Algoritmo para classificar os itens em uma determinada ordem.
Insert - Algoritmo para inserir item em uma estrutura de dados.
Update - Algoritmo para atualizar um item existente em uma estrutura de dados.
Delete - Algoritmo para excluir um item existente de uma estrutura de dados.

Características de um Algoritmo

Nem todos os procedimentos podem ser chamados de algoritmo. Um algoritmo deve ter as seguintes características -

Unambiguous- O algoritmo deve ser claro e inequívoco. Cada uma de suas etapas (ou fases) e suas entradas / saídas devem ser claras e levar a apenas um significado.
Input - Um algoritmo deve ter 0 ou mais entradas bem definidas.
Output - Um algoritmo deve ter 1 ou mais saídas bem definidas e deve corresponder à saída desejada.
Finiteness - Os algoritmos devem terminar após um número finito de etapas.
Feasibility - Deve ser viável com os recursos disponíveis.
Independent - Um algoritmo deve ter instruções passo a passo, que devem ser independentes de qualquer código de programação.

Como escrever um algoritmo?

Não existem padrões bem definidos para escrever algoritmos. Em vez disso, é dependente de problemas e recursos. Algoritmos nunca são escritos para suportar um código de programação específico.

Como sabemos, todas as linguagens de programação compartilham construções de código básicas como loops (do, for, while), controle de fluxo (if-else), etc. Essas construções comuns podem ser usadas para escrever um algoritmo.

Escrevemos algoritmos passo a passo, mas nem sempre é o caso. A escrita do algoritmo é um processo e é executada depois que o domínio do problema está bem definido. Ou seja, devemos conhecer o domínio do problema, para o qual estamos projetando uma solução.

Exemplo

Vamos tentar aprender a escrever algoritmos usando um exemplo.

Problem - Projete um algoritmo para adicionar dois números e exibir o resultado.

Step 1 − START
Step 2 − declare three integers a, b & c
Step 3 − define values of a & b
Step 4 − add values of a & b
Step 5 − store output of step 4 to c
Step 6 − print c
Step 7 − STOP

Os algoritmos informam aos programadores como codificar o programa. Alternativamente, o algoritmo pode ser escrito como -

Step 1 − START ADD
Step 2 − get values of a & b
Step 3 − c ← a + b
Step 4 − display c
Step 5 − STOP

No projeto e análise de algoritmos, geralmente o segundo método é usado para descrever um algoritmo. Isso torna mais fácil para o analista analisar o algoritmo, ignorando todas as definições indesejadas. Ele pode observar quais operações estão sendo usadas e como o processo está fluindo.

Escrita step numbers, é opcional.

Projetamos um algoritmo para obter a solução de um determinado problema. Um problema pode ser resolvido de mais de uma maneira.

Portanto, muitos algoritmos de solução podem ser derivados para um determinado problema. O próximo passo é analisar esses algoritmos de solução propostos e implementar a solução mais adequada.

Análise de Algoritmo

A eficiência de um algoritmo pode ser analisada em dois estágios diferentes, antes e após a implementação. Eles são os seguintes -

A Priori Analysis- Esta é uma análise teórica de um algoritmo. A eficiência de um algoritmo é medida assumindo que todos os outros fatores, por exemplo, a velocidade do processador, são constantes e não têm efeito na implementação.
A Posterior Analysis- Esta é uma análise empírica de um algoritmo. O algoritmo selecionado é implementado em linguagem de programação. Isso é então executado na máquina do computador de destino. Nesta análise, estatísticas reais, como tempo de execução e espaço necessário, são coletadas.

Vamos aprender sobre a análise de algoritmo a priori . A análise de algoritmo lida com a execução ou tempo de execução de várias operações envolvidas. O tempo de execução de uma operação pode ser definido como o número de instruções de computador executadas por operação.

Complexidade do Algoritmo

Suponha X é um algoritmo e n é o tamanho dos dados de entrada, o tempo e o espaço usados pelo algoritmo X são os dois fatores principais, que decidem a eficiência de X.

Time Factor - O tempo é medido contando o número de operações principais, como comparações no algoritmo de classificação.
Space Factor - O espaço é medido contando o espaço máximo de memória exigido pelo algoritmo.

A complexidade de um algoritmo f(n) dá o tempo de execução e / ou o espaço de armazenamento exigido pelo algoritmo em termos de n como o tamanho dos dados de entrada.

Complexidade do Espaço

A complexidade de espaço de um algoritmo representa a quantidade de espaço de memória exigida pelo algoritmo em seu ciclo de vida. O espaço exigido por um algoritmo é igual à soma dos dois componentes a seguir -

Uma parte fixa que é um espaço necessário para armazenar certos dados e variáveis, que são independentes do tamanho do problema. Por exemplo, variáveis simples e constantes usadas, tamanho do programa, etc.
Uma parte variável é um espaço requerido por variáveis, cujo tamanho depende do tamanho do problema. Por exemplo, alocação de memória dinâmica, espaço de pilha de recursão, etc.

A complexidade espacial S (P) de qualquer algoritmo P é S (P) = C + SP (I), onde C é a parte fixa e S (I) é a parte variável do algoritmo, que depende da característica de instância I. Seguinte é um exemplo simples que tenta explicar o conceito -

Algorithm: SUM(A, B)
Step 1 -  START
Step 2 -  C ← A + B + 10
Step 3 -  Stop

Aqui temos três variáveis A, B e C e uma constante. Portanto, S (P) = 1 + 3. Agora, o espaço depende dos tipos de dados de determinadas variáveis e tipos de constantes e será multiplicado de acordo.

Complexidade de tempo

A complexidade de tempo de um algoritmo representa a quantidade de tempo necessária para que o algoritmo seja executado até a conclusão. Os requisitos de tempo podem ser definidos como uma função numérica T (n), onde T (n) pode ser medido como o número de etapas, desde que cada etapa consuma um tempo constante.

Por exemplo, a adição de dois inteiros de n bits leva npassos. Conseqüentemente, o tempo computacional total é T (n) = c ∗ n, onde c é o tempo gasto para a adição de dois bits. Aqui, observamos que T (n) cresce linearmente conforme o tamanho da entrada aumenta.

A análise assintótica de um algoritmo refere-se à definição do limite / enquadramento matemático de seu desempenho em tempo de execução. Usando a análise assintótica, podemos muito bem concluir o melhor caso, o caso médio e o pior caso de um algoritmo.

A análise assintótica é limitada pela entrada, ou seja, se não houver entrada para o algoritmo, conclui-se que ele funciona em um tempo constante. Além da "entrada", todos os outros fatores são considerados constantes.

A análise assintótica refere-se ao cálculo do tempo de execução de qualquer operação em unidades matemáticas de computação. Por exemplo, o tempo de execução de uma operação é calculado como f (n) e pode ser para outra operação é calculado como g (n ² ). Isso significa que o tempo de execução da primeira operação aumentará linearmente com o aumento den e o tempo de execução da segunda operação aumentará exponencialmente quando naumenta. Da mesma forma, o tempo de execução de ambas as operações será quase o mesmo sen é significativamente pequeno.

Normalmente, o tempo exigido por um algoritmo cai em três tipos -

Best Case - Tempo mínimo necessário para a execução do programa.
Average Case - Tempo médio necessário para a execução do programa.
Worst Case - Tempo máximo necessário para a execução do programa.

Notações Assintóticas

A seguir estão as notações assintóticas comumente usadas para calcular a complexidade do tempo de execução de um algoritmo.

Ο Notação
Ω Notação
Notação θ

Big Oh Notation, Ο

A notação Ο (n) é a maneira formal de expressar o limite superior do tempo de execução de um algoritmo. Ele mede o pior caso de complexidade de tempo ou a maior quantidade de tempo que um algoritmo pode levar para ser concluído.

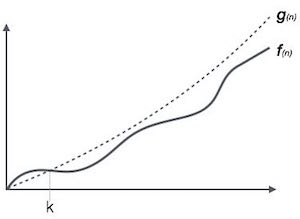
Por exemplo, para uma função f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n₀ such that f(n) ≤ c.g(n) for all n > n₀. }

Notação Omega, Ω

A notação Ω (n) é a maneira formal de expressar o limite inferior do tempo de execução de um algoritmo. Ele mede o melhor caso de complexidade de tempo ou a melhor quantidade de tempo que um algoritmo pode levar para ser concluído.

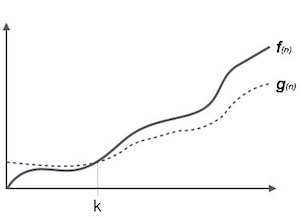
Por exemplo, para uma função f(n)

Ω(f(n)) ≥ { g(n) : there exists c > 0 and n₀ such that g(n) ≤ c.f(n) for all n > n₀. }

Notação Theta, θ

A notação θ (n) é a maneira formal de expressar o limite inferior e o limite superior do tempo de execução de um algoritmo. É representado da seguinte forma -

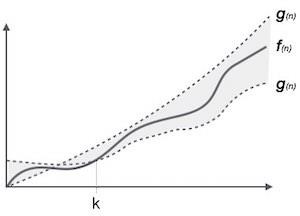
θ(f(n)) = { g(n) if and only if g(n) =  Ο(f(n)) and g(n) = Ω(f(n)) for all n > n₀. }

Notações assintóticas comuns

A seguir está uma lista de algumas notações assintóticas comuns -

constante	-	Ο (1)
logarítmico	-	Ο (log n)
linear	-	Ο (n)
n log n	-	Ο (n log n)
quadrático	-	Ο (n ² )
cúbico	-	Ο (n ³ )
polinomial	-	n ^{Ο (1)}
exponencial	-	2 ^{Ο (n)}

Um algoritmo é projetado para alcançar a solução ideal para um determinado problema. Na abordagem de algoritmo guloso, as decisões são feitas a partir do domínio de solução dado. Por ser ganancioso, é escolhida a solução mais próxima que parece fornecer uma solução ótima.

Algoritmos gananciosos tentam encontrar uma solução ótima localizada, que pode eventualmente levar a soluções globalmente otimizadas. No entanto, algoritmos geralmente gananciosos não fornecem soluções otimizadas globalmente.

Contando Moedas

Este problema é contar até um valor desejado escolhendo o mínimo possível de moedas e a abordagem gananciosa força o algoritmo a escolher a maior moeda possível. Se nos forem fornecidas moedas de $$ 1, 2, 5 e 10 e formos solicitados a contar $$ 18, o procedimento ganancioso será -

1 - Selecione uma moeda de $ 10, a contagem restante é 8
2 - Em seguida, selecione uma moeda de $ 5, a contagem restante é de 3
3 - Em seguida, selecione uma moeda de $ 2, a contagem restante é 1
4 - E, por fim, a seleção de uma moeda de 1 $ resolve o problema

Porém, parece estar funcionando bem, para esta contagem precisamos pegar apenas 4 moedas. Mas se mudarmos ligeiramente o problema, a mesma abordagem pode não ser capaz de produzir o mesmo resultado ótimo.

Para o sistema monetário, onde temos moedas de 1, 7, 10 valores, contar moedas para o valor 18 será absolutamente ideal, mas para contagens como 15, pode usar mais moedas do que o necessário. Por exemplo, a abordagem gananciosa usará 10 + 1 + 1 + 1 + 1 + 1, total de 6 moedas. Considerando que o mesmo problema poderia ser resolvido usando apenas 3 moedas (7 + 7 + 1)

Portanto, podemos concluir que a abordagem gananciosa escolhe uma solução otimizada imediata e pode falhar onde a otimização global é uma grande preocupação.

Exemplos

A maioria dos algoritmos de rede usa a abordagem gananciosa. Aqui está uma lista de alguns deles -

Problema do caixeiro viajante
Algoritmo de árvore de expansão mínima de Prim
Algoritmo de árvore de expansão mínima de Kruskal
Algoritmo de árvore de expansão mínima de Dijkstra
Gráfico - Colorir Mapa
Gráfico - Capa do Vértice
Problema da mochila
Problema de programação de trabalho

Existem muitos problemas semelhantes que usam a abordagem gananciosa para encontrar uma solução ideal.

Na abordagem dividir para conquistar, o problema em questão é dividido em subproblemas menores e cada problema é resolvido de forma independente. Quando continuamos a dividir os subproblemas em subproblemas ainda menores, podemos eventualmente atingir um estágio em que nenhuma divisão é possível. Esses menores subproblemas "atômicos" possíveis (frações) são resolvidos. A solução de todos os subproblemas é finalmente combinada para obter a solução de um problema original.

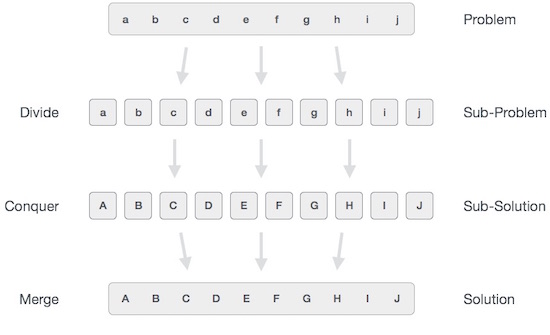
Em termos gerais, podemos entender divide-and-conquer abordagem em um processo de três etapas.

Divide / Break

Esta etapa envolve dividir o problema em subproblemas menores. Os subproblemas devem representar uma parte do problema original. Esta etapa geralmente usa uma abordagem recursiva para dividir o problema até que nenhum subproblema seja mais divisível. Nesse estágio, os subproblemas tornam-se atômicos por natureza, mas ainda representam uma parte do problema real.

Conquistar / Resolver

Esta etapa recebe muitos subproblemas menores a serem resolvidos. Geralmente, neste nível, os problemas são considerados 'resolvidos' por conta própria.

Unir / Combinar

Quando os subproblemas menores são resolvidos, esse estágio os combina recursivamente até que formem uma solução para o problema original. Esta abordagem algorítmica funciona recursivamente e as etapas de conquista e mesclagem funcionam tão próximas que aparecem como uma só.

Exemplos

Os seguintes algoritmos de computador são baseados em divide-and-conquer abordagem de programação -

Mesclar Classificar
Ordenação rápida
Pesquisa Binária
Multiplicação da matriz de Strassen
Par mais próximo (pontos)

Existem várias maneiras de resolver qualquer problema de computador, mas as mencionadas são um bom exemplo de abordagem de dividir para conquistar.

A abordagem de programação dinâmica é semelhante a dividir e conquistar, dividindo o problema em possíveis subproblemas menores e ainda menores. Mas ao contrário de, dividir e conquistar, esses subproblemas não são resolvidos de forma independente. Em vez disso, os resultados desses subproblemas menores são lembrados e usados para subproblemas semelhantes ou sobrepostos.

A programação dinâmica é usada onde temos problemas, que podem ser divididos em subproblemas semelhantes, para que seus resultados possam ser reutilizados. Principalmente, esses algoritmos são usados para otimização. Antes de resolver o subproblema em mãos, o algoritmo dinâmico tentará examinar os resultados dos subproblemas resolvidos anteriormente. As soluções dos subproblemas são combinadas para alcançar a melhor solução.

Então, podemos dizer que -

O problema deve ser capaz de ser dividido em subproblemas menores de sobreposição.
Uma solução ótima pode ser alcançada usando uma solução ótima de subproblemas menores.
Algoritmos dinâmicos usam Memoização.

Comparação

Em contraste com os algoritmos gulosos, onde a otimização local é abordada, os algoritmos dinâmicos são motivados para uma otimização geral do problema.

Em contraste com os algoritmos de dividir e conquistar, onde as soluções são combinadas para alcançar uma solução geral, os algoritmos dinâmicos usam a saída de um subproblema menor e então tentam otimizar um subproblema maior. Algoritmos dinâmicos usam Memoização para lembrar a saída de subproblemas já resolvidos.

Exemplo

Os seguintes problemas de computador podem ser resolvidos usando abordagem de programação dinâmica -

Série de números de Fibonacci
Problema de mochila
Torre de Hanói
Caminho mais curto para todos os pares por Floyd-Warshall
Caminho mais curto por Dijkstra
Agendamento de projeto

A programação dinâmica pode ser usada de cima para baixo e de baixo para cima. E, claro, na maioria das vezes, referir-se à saída da solução anterior é mais barato do que recomputar em termos de ciclos de CPU.

Este capítulo explica os termos básicos relacionados à estrutura de dados.

Definição de Dados

A definição de dados define um dado específico com as seguintes características.

Atomic - A definição deve definir um único conceito.
Traceable - A definição deve ser capaz de ser mapeada para algum elemento de dados.
Accurate - A definição deve ser inequívoca.
Clear and Concise - A definição deve ser compreensível.

Objeto de Dados

Objeto de dados representa um objeto que possui dados.

Tipo de dados

Tipo de dados é uma maneira de classificar vários tipos de dados, como inteiros, strings, etc., que determina os valores que podem ser usados com o tipo de dados correspondente, o tipo de operações que podem ser realizadas no tipo de dados correspondente. Existem dois tipos de dados -

Tipo de dados integrado
Tipo de dados derivados

Tipo de dados integrado

Esses tipos de dados para os quais uma linguagem tem suporte integrado são conhecidos como tipos de dados integrados. Por exemplo, a maioria das linguagens fornece os seguintes tipos de dados integrados.

Integers
Booleano (verdadeiro, falso)
Flutuante (números decimais)
Personagem e cordas

Tipo de dados derivados

Esses tipos de dados que são independentes da implementação, pois podem ser implementados de uma ou outra maneira, são conhecidos como tipos de dados derivados. Esses tipos de dados são normalmente criados pela combinação de tipos de dados primários ou integrados e operações associadas sobre eles. Por exemplo -

List
Array
Stack
Queue

Operações básicas

Os dados nas estruturas de dados são processados por certas operações. A estrutura de dados específica escolhida depende muito da frequência da operação que precisa ser executada na estrutura de dados.

Traversing
Searching
Insertion
Deletion
Sorting
Merging

Array é um contêiner que pode conter um número fixo de itens e esses itens devem ser do mesmo tipo. A maioria das estruturas de dados faz uso de arrays para implementar seus algoritmos. A seguir estão os termos importantes para entender o conceito de Array.

Element - Cada item armazenado em uma matriz é chamado de elemento.
Index - Cada localização de um elemento em uma matriz possui um índice numérico, que é usado para identificar o elemento.

Representação de Matriz

Os arrays podem ser declarados de várias maneiras em diferentes idiomas. Para ilustração, vamos tomar a declaração do array C.

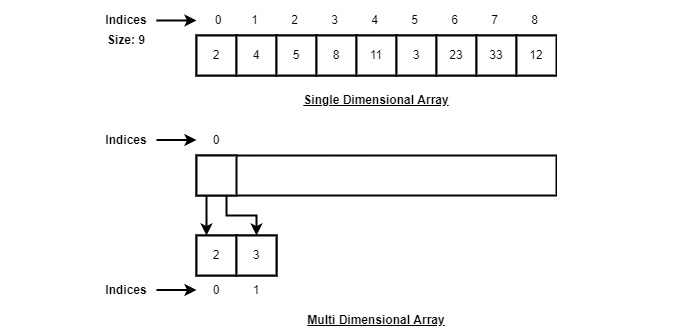
Conforme a ilustração acima, a seguir estão os pontos importantes a serem considerados.

O índice começa com 0.
O comprimento do array é 10, o que significa que ele pode armazenar 10 elementos.
Cada elemento pode ser acessado por meio de seu índice. Por exemplo, podemos buscar um elemento no índice 6 como 9.

Operações básicas

A seguir estão as operações básicas suportadas por uma matriz.

Traverse - imprime todos os elementos do array um por um.
Insertion - Adiciona um elemento no índice fornecido.
Deletion - Exclui um elemento no índice fornecido.
Search - Pesquisa um elemento usando o índice fornecido ou pelo valor.
Update - Atualiza um elemento no índice fornecido.

Em C, quando um array é inicializado com size, ele atribui valores padrão a seus elementos na seguinte ordem.

Tipo de dados	Valor padrão
bool	falso
Caracteres	0
int	0
flutuador	0,0
em dobro	0.0f
vazio
wchar_t	0

Operação transversal

Esta operação consiste em percorrer os elementos de uma matriz.

Exemplo

O programa a seguir percorre e imprime os elementos de uma matriz:

#include <stdio.h>
main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;   
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Quando compilamos e executamos o programa acima, ele produz o seguinte resultado -

Resultado

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8

Operação de Inserção

A operação de inserção é inserir um ou mais elementos de dados em uma matriz. Com base no requisito, um novo elemento pode ser adicionado no início, no final ou em qualquer índice da matriz.

Aqui, vemos uma implementação prática da operação de inserção, onde adicionamos dados no final da matriz -

Exemplo

A seguir está a implementação do algoritmo acima -

#include <stdio.h>

main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   
   printf("The original array elements are :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }

   n = n + 1;
	
   while( j >= k) {
      LA[j+1] = LA[j];
      j = j - 1;
   }

   LA[k] = item;

   printf("The array elements after insertion :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Quando compilamos e executamos o programa acima, ele produz o seguinte resultado -

Resultado

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after insertion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 10 
LA[4] = 7 
LA[5] = 8

Para outras variações da operação de inserção de matriz, clique aqui

Operação de Exclusão

A exclusão se refere à remoção de um elemento existente do array e à reorganização de todos os elementos de um array.

Algoritmo

Considerar LA é uma matriz linear com N elementos e K é um número inteiro positivo tal que K<=N. A seguir está o algoritmo para excluir um elemento disponível na K- ^ésima posição de LA.

1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA[J + 1]
5. Set J = J+1
6. Set N = N-1
7. Stop

Exemplo

A seguir está a implementação do algoritmo acima -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   j = k;
	
   while( j < n) {
      LA[j-1] = LA[j];
      j = j + 1;
   }
	
   n = n -1;
   
   printf("The array elements after deletion :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Quando compilamos e executamos o programa acima, ele produz o seguinte resultado -

Resultado

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after deletion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 7 
LA[3] = 8

Operação de Pesquisa

Você pode realizar uma pesquisa por um elemento da matriz com base em seu valor ou índice.

Algoritmo

Considerar LA é uma matriz linear com N elementos e K é um número inteiro positivo tal que K<=N. A seguir está o algoritmo para encontrar um elemento com um valor de ITEM usando a pesquisa sequencial.

1. Start
2. Set J = 0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop

Exemplo

A seguir está a implementação do algoritmo acima -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0, j = 0;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   while( j < n){
      if( LA[j] == item ) {
         break;
      }
		
      j = j + 1;
   }
	
   printf("Found element %d at position %d\n", item, j+1);
}

Quando compilamos e executamos o programa acima, ele produz o seguinte resultado -

Resultado

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
Found element 5 at position 3

Operação de atualização

A operação de atualização refere-se à atualização de um elemento existente da matriz em um determinado índice.

Algoritmo

Considerar LA é uma matriz linear com N elementos e K é um número inteiro positivo tal que K<=N. A seguir está o algoritmo para atualizar um elemento disponível na K- ^ésima posição de LA.

1. Start
2. Set LA[K-1] = ITEM
3. Stop

Exemplo

A seguir está a implementação do algoritmo acima -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5, item = 10;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   LA[k-1] = item;

   printf("The array elements after updation :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Quando compilamos e executamos o programa acima, ele produz o seguinte resultado -

Resultado

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after updation :
LA[0] = 1 
LA[1] = 3 
LA[2] = 10 
LA[3] = 7 
LA[4] = 8

Uma lista vinculada é uma sequência de estruturas de dados, que são conectadas por meio de links.

Lista vinculada é uma sequência de links que contém itens. Cada link contém uma conexão com outro link. A lista vinculada é a segunda estrutura de dados mais usada depois da matriz. A seguir estão os termos importantes para entender o conceito de Lista Vinculada.

Link - Cada link de uma lista vinculada pode armazenar dados chamados de elemento.
Next - Cada link de uma lista vinculada contém um link para o próximo link chamado Avançar.
LinkedList - Uma lista vinculada contém o link de conexão para o primeiro link denominado Primeiro.

Representação de lista vinculada

A lista vinculada pode ser visualizada como uma cadeia de nós, onde cada nó aponta para o próximo nó.

Conforme a ilustração acima, a seguir estão os pontos importantes a serem considerados.

A lista vinculada contém um elemento de link chamado primeiro.
Cada link carrega um (s) campo (s) de dados e um campo de link chamado next.
Cada link está vinculado ao seu próximo link usando o próximo link.
O último link carrega um link como nulo para marcar o fim da lista.

Tipos de lista vinculada

A seguir estão os vários tipos de lista vinculada.

Simple Linked List - A navegação do item é apenas para frente.
Doubly Linked List - Os itens podem ser navegados para frente e para trás.
Circular Linked List - O último item contém o link do primeiro elemento como próximo e o primeiro elemento contém um link para o último elemento como anterior.

Operações básicas

A seguir estão as operações básicas suportadas por uma lista.

Insertion - Adiciona um elemento no início da lista.
Deletion - Exclui um elemento do início da lista.
Display - Exibe a lista completa.
Search - Pesquisa um elemento usando a chave fornecida.
Delete - Exclui um elemento usando a chave fornecida.

Operação de Inserção

Adicionar um novo nó à lista vinculada é uma atividade de mais de uma etapa. Devemos aprender isso com diagramas aqui. Primeiro, crie um nó usando a mesma estrutura e encontre o local onde ele deve ser inserido.

Imagine que estamos inserindo um nó B (NewNode), entre A (LeftNode) e C(RightNode). Em seguida, aponte B. ao lado de C -

NewNode.next −> RightNode;

Deve ser assim -

Agora, o próximo nó à esquerda deve apontar para o novo nó.

LeftNode.next −> NewNode;

Isso colocará o novo nó no meio dos dois. A nova lista deve ser semelhante a esta -

Etapas semelhantes devem ser executadas se o nó estiver sendo inserido no início da lista. Ao inseri-lo no final, o penúltimo nó da lista deve apontar para o novo nó e o novo nó irá apontar para NULL.

Operação de Exclusão

A exclusão também é um processo de mais de uma etapa. Vamos aprender com a representação pictórica. Primeiro, localize o nó de destino a ser removido, usando algoritmos de pesquisa.

O nó esquerdo (anterior) do nó de destino agora deve apontar para o próximo nó do nó de destino -

LeftNode.next −> TargetNode.next;

Isso removerá o link que estava apontando para o nó de destino. Agora, usando o código a seguir, removeremos o que o nó de destino está apontando.

TargetNode.next −> NULL;

Precisamos usar o nó excluído. Podemos manter isso na memória, caso contrário, podemos simplesmente desalocar a memória e apagar o nó de destino completamente.

Operação reversa

Esta operação é completa. Precisamos fazer o último nó a ser apontado pelo nó principal e reverter toda a lista vinculada.

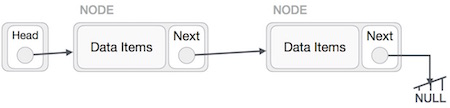
Primeiro, vamos até o final da lista. Deve estar apontando para NULL. Agora, faremos com que ele aponte para seu nó anterior -

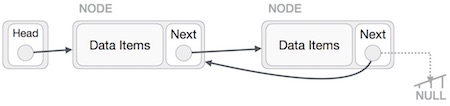
Temos que ter certeza de que o último nó não é o último nó. Portanto, teremos algum nó temporário, que se parece com o nó principal apontando para o último nó. Agora, faremos todos os nós do lado esquerdo apontarem para seus nós anteriores, um por um.

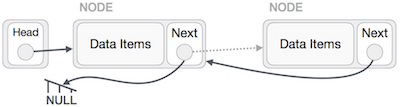
Exceto o nó (primeiro nó) apontado pelo nó principal, todos os nós devem apontar para seu predecessor, tornando-os seu novo sucessor. O primeiro nó apontará para NULL.

Faremos o nó principal apontar para o novo primeiro nó usando o nó temporário.

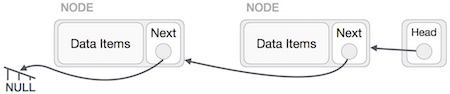
A lista vinculada agora está invertida. Para ver a implementação da lista vinculada na linguagem de programação C, clique aqui .

A lista duplamente vinculada é uma variação da lista vinculada na qual a navegação é possível de ambas as maneiras, tanto para frente quanto para trás facilmente em comparação com a lista vinculada única. A seguir estão os termos importantes para entender o conceito de lista duplamente vinculada.

Link - Cada link de uma lista vinculada pode armazenar dados chamados de elemento.
Next - Cada link de uma lista vinculada contém um link para o próximo link chamado Avançar.
Prev - Cada link de uma lista vinculada contém um link para o link anterior chamado Anterior.
LinkedList - Uma lista vinculada contém o link de conexão para o primeiro link chamado Primeiro e para o último link chamado Último.

Representação de lista duplamente vinculada

Conforme a ilustração acima, a seguir estão os pontos importantes a serem considerados.

A lista duplamente vinculada contém um elemento de link denominado primeiro e último.
Cada link carrega um campo (s) de dados e dois campos de link chamados next e prev.
Cada link está vinculado ao seu próximo link usando o próximo link.
Cada link está vinculado a seu link anterior usando seu link anterior.
O último link carrega um link como nulo para marcar o fim da lista.

Operações básicas

A seguir estão as operações básicas suportadas por uma lista.

Insertion - Adiciona um elemento no início da lista.
Deletion - Exclui um elemento do início da lista.
Insert Last - Adiciona um elemento no final da lista.
Delete Last - Exclui um elemento do final da lista.
Insert After - Adiciona um elemento após um item da lista.
Delete - Exclui um elemento da lista usando a tecla.
Display forward - Exibe a lista completa de uma maneira direta.
Display backward - Exibe a lista completa de forma reversa.

Operação de Inserção

O código a seguir demonstra a operação de inserção no início de uma lista duplamente vinculada.

Exemplo

//insert link at the first location
void insertFirst(int key, int data) {

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
	
   if(isEmpty()) {
      //make it the last link
      last = link;
   } else {
      //update first prev link
      head->prev = link;
   }

   //point it to old first link
   link->next = head;
	
   //point first to new first link
   head = link;
}

Operação de Exclusão

O código a seguir demonstra a operação de exclusão no início de uma lista duplamente vinculada.

Exemplo

//delete first item
struct node* deleteFirst() {

   //save reference to first link
   struct node *tempLink = head;
	
   //if only one link
   if(head->next == NULL) {
      last = NULL;
   } else {
      head->next->prev = NULL;
   }
	
   head = head->next;
	
   //return the deleted link
   return tempLink;
}

Inserção no final de uma operação

O código a seguir demonstra a operação de inserção na última posição de uma lista duplamente vinculada.

Exemplo

//insert link at the last location
void insertLast(int key, int data) {

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
	
   if(isEmpty()) {
      //make it the last link
      last = link;
   } else {
      //make link a new last link
      last->next = link;     
      
      //mark old last node as prev of new link
      link->prev = last;
   }

   //point last to new last node
   last = link;
}

Para ver a implementação na linguagem de programação C, clique aqui .

Lista vinculada circular é uma variação da lista vinculada na qual o primeiro elemento aponta para o último elemento e o último elemento aponta para o primeiro elemento. Tanto a Lista vinculada individualmente quanto a Lista vinculada dupla podem ser transformadas em uma lista vinculada circular.

Lista vinculada individualmente como circular

Na lista unida individualmente, o próximo ponteiro do último nó aponta para o primeiro nó.

Lista duplamente vinculada como circular

Na lista duplamente ligada, o próximo ponteiro do último nó aponta para o primeiro nó e o ponteiro anterior do primeiro nó aponta para o último nó que faz a circular em ambas as direções.

Conforme a ilustração acima, a seguir estão os pontos importantes a serem considerados.

O próximo link do último aponta para o primeiro link da lista em ambos os casos de lista unida ou duplamente vinculada.
O anterior do primeiro link aponta para o último da lista no caso de lista duplamente vinculada.

Operações básicas

A seguir estão as operações importantes apoiadas por uma lista circular.

insert - Insere um elemento no início da lista.
delete - Exclui um elemento do início da lista.
display - Exibe a lista.

Operação de Inserção

O código a seguir demonstra a operação de inserção em uma lista vinculada circular com base em uma lista vinculada única.

Exemplo

//insert link at the first location
void insertFirst(int key, int data) {
   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data= data;
	
   if (isEmpty()) {
      head = link;
      head->next = head;
   } else {
      //point it to old first node
      link->next = head;
		
      //point first to new first node
      head = link;
   }   
}

Operação de Exclusão

O código a seguir demonstra a operação de exclusão em uma lista vinculada circular com base em uma lista vinculada única.

//delete first item
struct node * deleteFirst() {
   //save reference to first link
   struct node *tempLink = head;
	
   if(head->next == head) {  
      head = NULL;
      return tempLink;
   }     

   //mark next to first link as first 
   head = head->next;
	
   //return the deleted link
   return tempLink;
}

Operação da lista de exibição

O código a seguir demonstra a operação da lista de exibição em uma lista ligada circular.

//display the list
void printList() {
   struct node *ptr = head;
   printf("\n[ ");
	
   //start from the beginning
   if(head != NULL) {
      while(ptr->next != ptr) {     
         printf("(%d,%d) ",ptr->key,ptr->data);
         ptr = ptr->next;
      }
   }
	
   printf(" ]");
}

Para saber sobre sua implementação na linguagem de programação C, clique aqui .

Uma pilha é um tipo abstrato de dados (ADT), comumente usado na maioria das linguagens de programação. É denominado pilha, pois se comporta como uma pilha do mundo real, por exemplo - um baralho de cartas ou uma pilha de pratos, etc.

Uma pilha do mundo real permite operações apenas em uma extremidade. Por exemplo, podemos colocar ou remover um cartão ou prato apenas do topo da pilha. Da mesma forma, Stack ADT permite todas as operações de dados em apenas uma extremidade. A qualquer momento, podemos acessar apenas o elemento superior de uma pilha.

Este recurso torna a estrutura de dados LIFO. LIFO significa Last-in-first-out. Aqui, o elemento que é colocado (inserido ou adicionado) por último é acessado primeiro. Na terminologia da pilha, a operação de inserção é chamadaPUSH operação e operação de remoção é chamada POP Operação.

Representação de pilha

O diagrama a seguir descreve uma pilha e suas operações -

Uma pilha pode ser implementada por meio de Array, Structure, Pointer e Linked List. A pilha pode ser de tamanho fixo ou pode ter uma sensação de redimensionamento dinâmico. Aqui, vamos implementar pilha usando arrays, o que a torna uma implementação de pilha de tamanho fixo.

Operações básicas

As operações de pilha podem envolver inicializar a pilha, usá-la e, em seguida, desinicializá-la. Além dessas coisas básicas, uma pilha é usada para as duas operações principais a seguir -

push() - Empurrar (armazenar) um elemento na pilha.
pop() - Remover (acessar) um elemento da pilha.

Quando os dados são colocados na pilha.

Para usar uma pilha com eficiência, precisamos verificar o status da pilha também. Para o mesmo propósito, a seguinte funcionalidade é adicionada às pilhas -

peek() - obtém o elemento de dados superior da pilha, sem removê-lo.
isFull() - verifique se a pilha está cheia.
isEmpty() - verifique se a pilha está vazia.

Em todos os momentos, mantemos um ponteiro para os últimos dados PUSHed na pilha. Como este ponteiro sempre representa o topo da pilha, portanto denominadotop. otop O ponteiro fornece o valor do topo da pilha sem realmente removê-lo.

Primeiro devemos aprender sobre os procedimentos para suportar funções de pilha -

olhadinha()

Algoritmo da função peek () -

begin procedure peek
   return stack[top]
end procedure

Implementação da função peek () na linguagem de programação C -

Example

int peek() {
   return stack[top];
}

está cheio()

Algoritmo da função isfull () -

begin procedure isfull

   if top equals to MAXSIZE
      return true
   else
      return false
   endif
   
end procedure

Implementação da função isfull () na linguagem de programação C -

Example

bool isfull() {
   if(top == MAXSIZE)
      return true;
   else
      return false;
}

está vazia()

Algoritmo da função isempty () -

begin procedure isempty

   if top less than 1
      return true
   else
      return false
   endif
   
end procedure

A implementação da função isempty () na linguagem de programação C é um pouco diferente. Inicializamos top em -1, pois o índice na matriz começa em 0. Portanto, verificamos se top está abaixo de zero ou -1 para determinar se a pilha está vazia. Aqui está o código -

Example

bool isempty() {
   if(top == -1)
      return true;
   else
      return false;
}

Operação Push

O processo de colocar um novo elemento de dados na pilha é conhecido como Operação Push. A operação push envolve uma série de etapas -

Step 1 - Verifica se a pilha está cheia.
Step 2 - Se a pilha estiver cheia, produz um erro e sai.
Step 3 - Se a pilha não estiver cheia, incrementos top para apontar o próximo espaço vazio.
Step 4 - Adiciona elemento de dados ao local da pilha, para onde o topo está apontando.
Step 5 - Retorna sucesso.

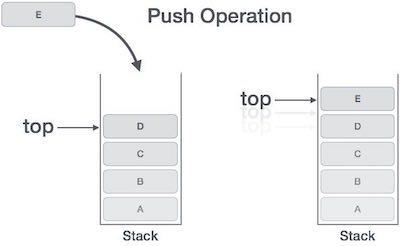
Se a lista encadeada for usada para implementar a pilha, na etapa 3, precisamos alocar espaço dinamicamente.

Algoritmo para Operação PUSH

Um algoritmo simples para operação Push pode ser derivado da seguinte forma -

begin procedure push: stack, data

   if stack is full
      return null
   endif
   
   top ← top + 1
   stack[top] ← data

end procedure

A implementação deste algoritmo em C é muito fácil. Veja o seguinte código -

Example

void push(int data) {
   if(!isFull()) {
      top = top + 1;   
      stack[top] = data;
   } else {
      printf("Could not insert data, Stack is full.\n");
   }
}

Operação Pop

Acessar o conteúdo removendo-o da pilha é conhecido como Operação Pop. Em uma implementação de array da operação pop (), o elemento de dados não é realmente removido, em vez dissotopé diminuído para uma posição inferior na pilha para apontar para o próximo valor. Mas na implementação de lista vinculada, pop () realmente remove o elemento de dados e desaloca o espaço de memória.

Uma operação Pop pode envolver as seguintes etapas -

Step 1 - Verifica se a pilha está vazia.
Step 2 - Se a pilha estiver vazia, produz um erro e sai.
Step 3 - Se a pilha não estiver vazia, acessa o elemento de dados no qual top está apontando.
Step 4 - Diminui o valor do topo em 1.
Step 5 - Retorna sucesso.

Algoritmo para Operação Pop

Um algoritmo simples para a operação Pop pode ser derivado da seguinte maneira -

begin procedure pop: stack

   if stack is empty
      return null
   endif
   
   data ← stack[top]
   top ← top - 1
   return data

end procedure

A implementação deste algoritmo em C é a seguinte -

Example

int pop(int data) {

   if(!isempty()) {
      data = stack[top];
      top = top - 1;   
      return data;
   } else {
      printf("Could not retrieve data, Stack is empty.\n");
   }
}

Para um programa de pilha completo em linguagem de programação C, clique aqui .

A forma de escrever expressões aritméticas é conhecida como notation. Uma expressão aritmética pode ser escrita em três notações diferentes, mas equivalentes, ou seja, sem alterar a essência ou a saída de uma expressão. Essas notações são -

Notação Infix
Notação de prefixo (polonês)
Notação Postfix (polonês reverso)

Essas notações são nomeadas como usam o operador na expressão. Devemos aprender o mesmo aqui neste capítulo.

Notação Infix

Nós escrevemos expressão em infix notação, por exemplo, a - b + c, onde os operadores são usados in-entre operandos. É fácil para nós, humanos, ler, escrever e falar em notação infixa, mas o mesmo não funciona bem com dispositivos de computação. Um algoritmo para processar notação de infixação pode ser difícil e caro em termos de consumo de tempo e espaço.

Notação de prefixo

Nesta notação, o operador é prefixed para operandos, ou seja, o operador é escrito antes dos operandos. Por exemplo,+ab. Isso é equivalente à sua notação infixaa + b. A notação de prefixo também é conhecida comoPolish Notation.

Notação Postfix

Este estilo de notação é conhecido como Reversed Polish Notation. Neste estilo de notação, o operador épostfixed para os operandos, ou seja, o operador é escrito após os operandos. Por exemplo,ab+. Isso é equivalente à sua notação infixaa + b.

A tabela a seguir tenta mostrar brevemente a diferença em todas as três notações -

Sr. Não.	Notação Infix	Notação de prefixo	Notação Postfix
1	a + b	+ ab	ab +
2	(a + b) ∗ c	∗ + abc	ab + c ∗
3	a ∗ (b + c)	∗ a + bc	abc + ∗
4	a / b + c / d	+ / ab / cd	ab / cd / +
5	(a + b) ∗ (c + d)	∗ + ab + cd	ab + cd + ∗
6	((a + b) ∗ c) - d	- ∗ + abcd	ab + c ∗ d -

Análise de expressões

Como discutimos, não é uma maneira muito eficiente de projetar um algoritmo ou programa para analisar notações infixas. Em vez disso, essas notações infixas são primeiro convertidas em notações pós-fixadas ou prefixadas e depois calculadas.

Para analisar qualquer expressão aritmética, precisamos cuidar também da precedência do operador e da associatividade.

Precedência

Quando um operando está entre dois operadores diferentes, qual operador assumirá o operando primeiro, é decidido pela precedência de um operador sobre os outros. Por exemplo -

Como a operação de multiplicação tem precedência sobre a adição, b * c será avaliado primeiro. Uma tabela de precedência de operador é fornecida posteriormente.

Associatividade

A associatividade descreve a regra em que os operadores com a mesma precedência aparecem em uma expressão. Por exemplo, na expressão a + b - c, ambos + e - têm a mesma precedência, então qual parte da expressão será avaliada primeiro, é determinada pela associatividade desses operadores. Aqui, + e - são associativos à esquerda, então a expressão será avaliada como(a + b) − c.

A precedência e a associatividade determinam a ordem de avaliação de uma expressão. A seguir está uma tabela de precedência e associatividade do operador (da mais alta para a mais baixa) -

Sr. Não.	Operador	Precedência	Associatividade
1	Exponenciação ^	Altíssima	Associativo certo
2	Multiplicação (∗) e divisão (/)	Segundo mais alto	Esquerda Associativa
3	Adição (+) e subtração (-)	O mais baixo	Esquerda Associativa

A tabela acima mostra o comportamento padrão dos operadores. A qualquer momento na avaliação da expressão, a ordem pode ser alterada usando parênteses. Por exemplo -

Dentro a + b*c, a parte da expressão b*cserá avaliado primeiro, com a multiplicação como precedência sobre a adição. Aqui usamos parênteses paraa + b para ser avaliado primeiro, como (a + b)*c.

Algoritmo de avaliação Postfix

Devemos agora olhar para o algoritmo sobre como avaliar a notação pós-fixada -

Step 1 − scan the expression from left to right 
Step 2 − if it is an operand push it to stack 
Step 3 − if it is an operator pull operand from stack and perform operation 
Step 4 − store the output of step 3, back to stack 
Step 5 − scan the expression until all operands are consumed 
Step 6 − pop the stack and perform operation

Para ver a implementação na linguagem de programação C, clique aqui .

Fila é uma estrutura de dados abstrata, um tanto semelhante às Pilhas. Ao contrário das pilhas, uma fila está aberta em ambas as extremidades. Uma extremidade é sempre usada para inserir dados (enfileirar) e a outra é usada para remover dados (desenfileirar). A fila segue a metodologia First-In-First-Out, ou seja, o item de dados armazenado primeiro será acessado primeiro.

Um exemplo do mundo real de fila pode ser uma estrada de mão única de faixa única, onde o veículo entra primeiro, sai primeiro. Mais exemplos do mundo real podem ser vistos como filas nos guichês e pontos de ônibus.

Representação de fila

Como agora entendemos que na fila, acessamos as duas extremidades por motivos diferentes. O diagrama a seguir fornecido abaixo tenta explicar a representação da fila como estrutura de dados -

Como nas pilhas, uma fila também pode ser implementada usando Arrays, Linked-lists, Pointers e Structures. Para fins de simplicidade, devemos implementar filas usando array unidimensional.

Operações básicas

As operações de fila podem envolver inicializar ou definir a fila, utilizá-la e, em seguida, apagá-la completamente da memória. Aqui, devemos tentar entender as operações básicas associadas às filas -

enqueue() - adicionar (armazenar) um item à fila.
dequeue() - remover (acessar) um item da fila.

Poucas funções a mais são necessárias para tornar eficiente a operação de fila mencionada acima. Estes são -

peek() - Obtém o elemento na frente da fila sem removê-lo.
isfull() - Verifica se a fila está cheia.
isempty() - Verifica se a fila está vazia.

Na fila, sempre retiramos da fila (ou acessamos) dados, apontados por front ponteiro e enquanto enfileiramos (ou armazenamos) dados na fila, ajudamos rear ponteiro.

Vamos primeiro aprender sobre as funções de suporte de uma fila -

olhadinha()

Esta função ajuda a ver os dados no frontda fila. O algoritmo da função peek () é o seguinte -

Algorithm

begin procedure peek
   return queue[front]
end procedure

Implementação da função peek () na linguagem de programação C -

Example

int peek() {
   return queue[front];
}

está cheio()

Como estamos usando uma matriz de dimensão única para implementar a fila, apenas verificamos se o ponteiro traseiro atinge MAXSIZE para determinar se a fila está cheia. No caso de mantermos a fila em uma lista ligada circular, o algoritmo será diferente. Algoritmo da função isfull () -

Algorithm

begin procedure isfull

   if rear equals to MAXSIZE
      return true
   else
      return false
   endif
   
end procedure

Implementação da função isfull () na linguagem de programação C -

Example

bool isfull() {
   if(rear == MAXSIZE - 1)
      return true;
   else
      return false;
}

está vazia()

Algoritmo da função isempty () -

Algorithm

begin procedure isempty

   if front is less than MIN  OR front is greater than rear
      return true
   else
      return false
   endif
   
end procedure

Se o valor de front for menor que MIN ou 0, indica que a fila ainda não foi inicializada, portanto está vazia.

Aqui está o código de programação C -

Example

bool isempty() {
   if(front < 0 || front > rear) 
      return true;
   else
      return false;
}

Operação de enfileiramento

As filas mantêm dois indicadores de dados, front e rear. Portanto, suas operações são comparativamente difíceis de implementar do que as de pilhas.

As etapas a seguir devem ser realizadas para enfileirar (inserir) dados em uma fila -

Step 1 - Verifique se a fila está cheia.
Step 2 - Se a fila estiver cheia, produza um erro de estouro e saia.
Step 3 - Se a fila não estiver cheia, incremente rear ponteiro para apontar o próximo espaço vazio.
Step 4 - Adicione o elemento de dados ao local da fila, para onde a parte traseira está apontando.
Step 5 - sucesso de retorno.

Às vezes, também verificamos se uma fila foi inicializada ou não, para lidar com qualquer situação imprevista.

Algoritmo para operação de enfileiramento

procedure enqueue(data)      
   
   if queue is full
      return overflow
   endif
   
   rear ← rear + 1
   queue[rear] ← data
   return true
   
end procedure

Implementação de enqueue () na linguagem de programação C -

Example

int enqueue(int data)      
   if(isfull())
      return 0;
   
   rear = rear + 1;
   queue[rear] = data;
   
   return 1;
end procedure

Operação de desenfileiramento

Acessar dados da fila é um processo de duas tarefas - acessar os dados onde frontestá apontando e remove os dados após o acesso. As seguintes etapas são realizadas para realizardequeue operação -

Step 1 - Verifique se a fila está vazia.
Step 2 - Se a fila estiver vazia, produz um erro de underflow e sai.
Step 3 - Se a fila não estiver vazia, acesse os dados onde front está apontando.
Step 4 - Incrementar front ponteiro para apontar para o próximo elemento de dados disponível.
Step 5 - Retorno com sucesso.

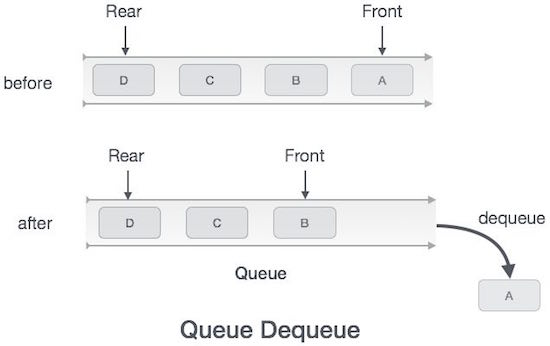
Algoritmo para operação de desenfileiramento

procedure dequeue
   
   if queue is empty
      return underflow
   end if

   data = queue[front]
   front ← front + 1
   return true

end procedure

Implementação de dequeue () na linguagem de programação C -

Example

int dequeue() {
   if(isempty())
      return 0;

   int data = queue[front];
   front = front + 1;

   return data;
}

Para obter um programa Queue completo na linguagem de programação C, clique aqui .

A pesquisa linear é um algoritmo de pesquisa muito simples. Nesse tipo de busca, uma busca sequencial é feita em todos os itens um a um. Cada item é verificado e se uma correspondência for encontrada, esse item específico é retornado, caso contrário, a pesquisa continua até o final da coleta de dados.

Algoritmo

Linear Search ( Array A, Value x)

Step 1: Set i to 1
Step 2: if i > n then go to step 7
Step 3: if A[i] = x then go to step 6
Step 4: Set i to i + 1
Step 5: Go to Step 2
Step 6: Print Element x Found at index i and go to step 8
Step 7: Print element not found
Step 8: Exit

Pseudo-código

procedure linear_search (list, value)

   for each item in the list
      if match item == value
         return the item's location
      end if
   end for

end procedure

Para saber sobre a implementação de pesquisa linear na linguagem de programação C, clique aqui .

A pesquisa binária é um algoritmo de pesquisa rápida com complexidade de tempo de execução de Ο (log n). Este algoritmo de pesquisa funciona com o princípio de dividir para conquistar. Para que esse algoritmo funcione corretamente, a coleta de dados deve estar na forma classificada.

A pesquisa binária procura um item específico, comparando o item mais intermediário da coleção. Se ocorrer uma correspondência, o índice do item será retornado. Se o item do meio for maior que o item, o item será pesquisado na submatriz à esquerda do item do meio. Caso contrário, o item é pesquisado na submatriz à direita do item do meio. Este processo continua na submatriz também até que o tamanho da submatriz seja reduzido a zero.

Como funciona a pesquisa binária?

Para que uma pesquisa binária funcione, é obrigatório que a matriz de destino seja classificada. Aprenderemos o processo de busca binária com um exemplo pictórico. A seguir está nossa matriz classificada e vamos supor que precisamos pesquisar a localização do valor 31 usando a pesquisa binária.

Primeiro, devemos determinar metade da matriz usando esta fórmula -

mid = low + (high - low) / 2

Aqui está, 0 + (9 - 0) / 2 = 4 (valor inteiro de 4,5). Portanto, 4 é o meio da matriz.

Agora comparamos o valor armazenado na localização 4 com o valor que está sendo pesquisado, ou seja, 31. Descobrimos que o valor na localização 4 é 27, o que não é uma correspondência. Como o valor é maior que 27 e temos uma matriz classificada, também sabemos que o valor de destino deve estar na parte superior da matriz.

Mudamos nosso mínimo para médio + 1 e encontramos o novo valor médio novamente.

low = mid + 1
mid = low + (high - low) / 2

Nosso novo mid é 7 agora. Comparamos o valor armazenado no local 7 com nosso valor alvo 31.

O valor armazenado no local 7 não corresponde, mas é mais do que procuramos. Portanto, o valor deve estar na parte inferior deste local.

Portanto, calculamos o meio novamente. Desta vez, são 5.

Comparamos o valor armazenado no local 5 com nosso valor alvo. Descobrimos que é uma combinação.

Concluímos que o valor alvo 31 está armazenado na localização 5.

A pesquisa binária divide pela metade os itens pesquisáveis e, portanto, reduz a contagem de comparações a serem feitas a muito menos números.

Pseudo-código

O pseudocódigo dos algoritmos de pesquisa binária deve ser semelhante a este -

Procedure binary_search
   A ← sorted array
   n ← size of array
   x ← value to be searched

   Set lowerBound = 1
   Set upperBound = n 

   while x not found
      if upperBound < lowerBound 
         EXIT: x does not exists.
   
      set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
      
      if A[midPoint] < x
         set lowerBound = midPoint + 1
         
      if A[midPoint] > x
         set upperBound = midPoint - 1 

      if A[midPoint] = x 
         EXIT: x found at location midPoint
   end while
   
end procedure

Para saber sobre a implementação de pesquisa binária usando array na linguagem de programação C, clique aqui .

A pesquisa de interpolação é uma variante aprimorada da pesquisa binária. Este algoritmo de pesquisa funciona na posição de sondagem do valor necessário. Para que esse algoritmo funcione corretamente, a coleta de dados deve ser ordenada e igualmente distribuída.

A pesquisa binária tem uma grande vantagem de complexidade de tempo sobre a pesquisa linear. A pesquisa linear tem complexidade de pior caso de Ο (n), enquanto a pesquisa binária tem Ο (log n).

Existem casos em que a localização dos dados alvo pode ser conhecida com antecedência. Por exemplo, no caso de uma lista telefônica, se quisermos pesquisar o número de telefone de Morphius. Aqui, a pesquisa linear e até a pesquisa binária parecerão lentas, pois podemos pular diretamente para o espaço da memória onde os nomes que começam com 'M' são armazenados.

Posicionamento na pesquisa binária

Na pesquisa binária, se os dados desejados não forem encontrados, o restante da lista é dividido em duas partes, inferior e superior. A busca é realizada em qualquer um deles.

Mesmo quando os dados são classificados, a pesquisa binária não aproveita para sondar a posição dos dados desejados.

Sondagem de posição na pesquisa de interpolação

A pesquisa de interpolação encontra um item específico calculando a posição da sonda. Inicialmente, a posição da sonda é a posição do item mais central da coleção.

Se ocorrer uma correspondência, o índice do item será retornado. Para dividir a lista em duas partes, usamos o seguinte método -

mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])

where −
   A    = list
   Lo   = Lowest index of the list
   Hi   = Highest index of the list
   A[n] = Value stored at index n in the list

Se o item do meio for maior que o item, então a posição da sonda é calculada novamente na submatriz à direita do item do meio. Caso contrário, o item é pesquisado na submatriz à esquerda do item do meio. Esse processo continua na submatriz também até que o tamanho da submatriz seja reduzido a zero.

A complexidade do tempo de execução do algoritmo de pesquisa de interpolação é Ο(log (log n)) em comparação com Ο(log n) do BST em situações favoráveis.

Algoritmo

Como é uma improvisação do algoritmo BST existente, estamos mencionando as etapas para pesquisar o índice de valor de dados 'alvo', usando sondagem de posição -

Step 1 − Start searching data from middle of the list.
Step 2 − If it is a match, return the index of the item, and exit.
Step 3 − If it is not a match, probe position.
Step 4 − Divide the list using probing formula and find the new midle.
Step 5 − If data is greater than middle, search in higher sub-list.
Step 6 − If data is smaller than middle, search in lower sub-list.
Step 7 − Repeat until match.

Pseudo-código

A → Array list
N → Size of A
X → Target Value

Procedure Interpolation_Search()

   Set Lo  →  0
   Set Mid → -1
   Set Hi  →  N-1

   While X does not match
   
      if Lo equals to Hi OR A[Lo] equals to A[Hi]
         EXIT: Failure, Target not found
      end if
      
      Set Mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo]) 

      if A[Mid] = X
         EXIT: Success, Target found at Mid
      else 
         if A[Mid] < X
            Set Lo to Mid+1
         else if A[Mid] > X
            Set Hi to Mid-1
         end if
      end if
   End While

End Procedure

Para saber sobre a implementação da busca de interpolação na linguagem de programação C, clique aqui .

Hash Table é uma estrutura de dados que armazena dados de forma associativa. Em uma tabela hash, os dados são armazenados em um formato de matriz, em que cada valor de dados tem seu próprio valor de índice exclusivo. O acesso aos dados torna-se muito rápido se conhecermos o índice dos dados desejados.

Assim, torna-se uma estrutura de dados em que as operações de inserção e busca são muito rápidas, independentemente do tamanho dos dados. A tabela de hash usa uma matriz como meio de armazenamento e usa a técnica de hash para gerar um índice onde um elemento deve ser inserido ou localizado.

Hashing

Hashing é uma técnica para converter um intervalo de valores-chave em um intervalo de índices de uma matriz. Vamos usar o operador de módulo para obter uma gama de valores-chave. Considere um exemplo de tabela hash de tamanho 20 e os seguintes itens devem ser armazenados. Os itens estão no formato (chave, valor).

(1,20)
(2,70)
(42,80)
(4,25)
(12,44)
(14,32)
(17,11)
(13,78)
(37,98)

Sr. Não.	Chave	Cerquilha	Índice Array
1	1	1% 20 = 1	1
2	2	2% 20 = 2	2
3	42	42% 20 = 2	2
4	4	4% 20 = 4	4
5	12	12% 20 = 12	12
6	14	14% 20 = 14	14
7	17	17% 20 = 17	17
8	13	13% 20 = 13	13
9	37	37% 20 = 17	17

Sondagem Linear

Como podemos ver, pode acontecer que a técnica de hashing seja usada para criar um índice já usado do array. Nesse caso, podemos pesquisar o próximo local vazio na matriz olhando para a próxima célula até encontrar uma célula vazia. Essa técnica é chamada de sondagem linear.

Sr. Não.	Chave	Cerquilha	Índice Array	Após a análise linear, índice de matriz
1	1	1% 20 = 1	1	1
2	2	2% 20 = 2	2	2
3	42	42% 20 = 2	2	3
4	4	4% 20 = 4	4	4
5	12	12% 20 = 12	12	12
6	14	14% 20 = 14	14	14
7	17	17% 20 = 17	17	17
8	13	13% 20 = 13	13	13
9	37	37% 20 = 17	17	18

Operações básicas

A seguir estão as operações primárias básicas de uma tabela hash.

Search - Pesquisa um elemento em uma tabela hash.
Insert - insere um elemento em uma tabela hash.
delete - Exclui um elemento de uma tabela hash.

Item de dados

Defina um item de dados com alguns dados e chave, com base nos quais a pesquisa será conduzida em uma tabela hash.

struct DataItem {
   int data;
   int key;
};

Método Hash

Defina um método de hashing para calcular o código hash da chave do item de dados.

int hashCode(int key){
   return key % SIZE;
}

Operação de Pesquisa

Sempre que um elemento deve ser pesquisado, calcule o código hash da chave passada e localize o elemento usando esse código hash como índice na matriz. Use a análise linear para obter o elemento à frente se o elemento não for encontrado no código hash calculado.

Exemplo

struct DataItem *search(int key) {
   //get the hash
   int hashIndex = hashCode(key);
	
   //move in array until an empty
   while(hashArray[hashIndex] != NULL) {
	
      if(hashArray[hashIndex]->key == key)
         return hashArray[hashIndex];
			
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }

   return NULL;        
}

Operação de inserção

Sempre que um elemento deve ser inserido, calcule o código hash da chave passada e localize o índice usando esse código hash como um índice na matriz. Use sondagem linear para localização vazia, se um elemento for encontrado no código hash calculado.

Exemplo

void insert(int key,int data) {
   struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
   item->data = data;  
   item->key = key;     

   //get the hash 
   int hashIndex = hashCode(key);

   //move in array until an empty or deleted cell
   while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }
	
   hashArray[hashIndex] = item;        
}

Excluir operação

Sempre que um elemento deve ser excluído, calcule o código hash da chave passada e localize o índice usando esse código hash como um índice na matriz. Use a análise linear para obter o elemento adiante se um elemento não for encontrado no código hash calculado. Quando encontrado, armazene um item fictício para manter o desempenho da tabela hash intacto.

Exemplo

struct DataItem* delete(struct DataItem* item) {
   int key = item->key;

   //get the hash 
   int hashIndex = hashCode(key);

   //move in array until an empty 
   while(hashArray[hashIndex] !=NULL) {
	
      if(hashArray[hashIndex]->key == key) {
         struct DataItem* temp = hashArray[hashIndex]; 
			
         //assign a dummy item at deleted position
         hashArray[hashIndex] = dummyItem; 
         return temp;
      } 
		
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }  
	
   return NULL;        
}

Para saber sobre a implementação de hash na linguagem de programação C, clique aqui .

A classificação refere-se a organizar os dados em um formato específico. O algoritmo de classificação especifica a maneira de organizar os dados em uma ordem específica. As ordens mais comuns são em ordem numérica ou lexicográfica.

A importância da classificação reside no fato de que a pesquisa de dados pode ser otimizada em um nível muito alto, se os dados forem armazenados de maneira classificada. A classificação também é usada para representar dados em formatos mais legíveis. A seguir estão alguns exemplos de classificação em cenários da vida real -

Telephone Directory - A lista telefônica armazena os números de telefone das pessoas classificadas por seus nomes, para que os nomes possam ser pesquisados facilmente.
Dictionary - O dicionário armazena as palavras em ordem alfabética para facilitar a busca por qualquer palavra.

Classificação no local e não no local

Os algoritmos de classificação podem exigir algum espaço extra para comparação e armazenamento temporário de alguns elementos de dados. Esses algoritmos não requerem nenhum espaço extra e a classificação ocorre no local ou, por exemplo, dentro do próprio array. Isso é chamadoin-place sorting. A classificação por bolha é um exemplo de classificação no local.

No entanto, em alguns algoritmos de classificação, o programa requer espaço maior ou igual aos elementos sendo classificados. A classificação que usa igual ou mais espaço é chamadanot-in-place sorting. Merge-sort é um exemplo de classificação não no local.

Classificação estável e não estável

Se um algoritmo de classificação, após classificar o conteúdo, não alterar a sequência de conteúdo semelhante em que aparecem, ele é chamado stable sorting.

Se um algoritmo de classificação, após classificar o conteúdo, alterar a sequência de conteúdo semelhante em que aparecem, ele é chamado unstable sorting.

A estabilidade de um algoritmo é importante quando desejamos manter a sequência dos elementos originais, como em uma tupla, por exemplo.

Algoritmo de classificação adaptativo e não adaptativo

Um algoritmo de classificação é considerado adaptativo, se tirar vantagem de elementos já 'classificados' na lista a ser classificada. Ou seja, ao classificar se a lista de fontes já possui algum elemento classificado, os algoritmos adaptativos levarão isso em consideração e tentarão não reordená-los.

Um algoritmo não adaptativo é aquele que não leva em consideração os elementos já classificados. Eles tentam forçar cada elemento a ser reordenado para confirmar sua classificação.

Termos importantes

Alguns termos são geralmente cunhados durante a discussão de técnicas de classificação, aqui está uma breve introdução a eles -

Ordem crescente

Uma sequência de valores está em increasing order, se o elemento sucessivo for maior que o anterior. Por exemplo, 1, 3, 4, 6, 8, 9 estão em ordem crescente, pois cada próximo elemento é maior do que o elemento anterior.

Ordem Decrescente

Uma sequência de valores está em decreasing order, se o elemento sucessivo for menor que o atual. Por exemplo, 9, 8, 6, 4, 3, 1 estão em ordem decrescente, pois cada próximo elemento é menor do que o elemento anterior.

Ordem não crescente

Uma sequência de valores está em non-increasing order, se o elemento sucessivo for menor ou igual ao elemento anterior na sequência. Essa ordem ocorre quando a sequência contém valores duplicados. Por exemplo, 9, 8, 6, 3, 3, 1 estão em ordem não crescente, pois cada próximo elemento é menor ou igual (no caso de 3), mas não maior do que qualquer elemento anterior.

Ordem não decrescente

Uma sequência de valores está em non-decreasing order, se o elemento sucessivo for maior ou igual ao seu elemento anterior na sequência. Essa ordem ocorre quando a sequência contém valores duplicados. Por exemplo, 1, 3, 3, 6, 8, 9 estão em ordem não decrescente, pois cada próximo elemento é maior ou igual (no caso de 3), mas não menor que o anterior.

A classificação por bolha é um algoritmo de classificação simples. Este algoritmo de classificação é um algoritmo baseado em comparação em que cada par de elementos adjacentes é comparado e os elementos são trocados se não estiverem em ordem. Este algoritmo não é adequado para grandes conjuntos de dados, pois sua complexidade média e de pior caso são de Ο (n ² ), onden é o número de itens.

Como funciona a classificação por bolha?

Pegamos um array não classificado como nosso exemplo. A classificação por bolha leva Ο (n ² ) tempo, portanto, estamos mantendo-a curta e precisa.

A classificação por bolha começa com os dois primeiros elementos, comparando-os para verificar qual é o maior.

Nesse caso, o valor 33 é maior que 14, portanto, já está nos locais classificados. Em seguida, comparamos 33 com 27.

Descobrimos que 27 é menor que 33 e esses dois valores devem ser trocados.

A nova matriz deve ser semelhante a esta -

Em seguida, comparamos 33 e 35. Descobrimos que ambos já estão em posições ordenadas.

Em seguida, passamos para os próximos dois valores, 35 e 10.

Sabemos então que 10 é menor que 35. Portanto, eles não são classificados.

Trocamos esses valores. Descobrimos que atingimos o final da matriz. Após uma iteração, o array deve ficar assim -

Para ser preciso, agora estamos mostrando como um array deve ficar após cada iteração. Após a segunda iteração, deve ficar assim -

Observe que após cada iteração, pelo menos um valor se move no final.

E quando não há necessidade de troca, o bubble sorts aprende que um array está completamente classificado.

Agora devemos examinar alguns aspectos práticos do tipo de bolha.

Algoritmo

Nós presumimos list é uma matriz de nelementos Além disso, assumimos queswap a função troca os valores dos elementos da matriz fornecidos.

begin BubbleSort(list)

   for all elements of list
      if list[i] > list[i+1]
         swap(list[i], list[i+1])
      end if
   end for
   
   return list
   
end BubbleSort

Pseudo-código

Observamos no algoritmo que o Bubble Sort compara cada par de elementos do array, a menos que todo o array esteja completamente classificado em ordem crescente. Isso pode causar alguns problemas de complexidade, como o que aconteceria se o array não precisasse mais de troca, pois todos os elementos já estão em ascensão.

Para amenizar o problema, usamos uma variável sinalizador swappedo que nos ajudará a ver se alguma troca aconteceu ou não. Se nenhuma troca ocorreu, ou seja, o array não requer mais processamento para ser classificado, ele sairá do loop.

O pseudocódigo do algoritmo BubbleSort pode ser escrito da seguinte maneira -

procedure bubbleSort( list : array of items )

   loop = list.count;
   
   for i = 0 to loop-1 do:
      swapped = false
		
      for j = 0 to loop-1 do:
      
         /* compare the adjacent elements */   
         if list[j] > list[j+1] then
            /* swap them */
            swap( list[j], list[j+1] )		 
            swapped = true
         end if
         
      end for
      
      /*if no number was swapped that means 
      array is sorted now, break the loop.*/
      
      if(not swapped) then
         break
      end if
      
   end for
   
end procedure return list

Implementação

Mais um problema que não abordamos em nosso algoritmo original e seu pseudocódigo improvisado, é que, após cada iteração, os valores mais altos se estabelecem no final do array. Portanto, a próxima iteração não precisa incluir elementos já classificados. Para esse propósito, em nossa implementação, restringimos o loop interno para evitar valores já classificados.

Para saber sobre a implementação de classificação por bolha na linguagem de programação C, clique aqui .

Este é um algoritmo de classificação baseado em comparação no local. Aqui, uma sub-lista é mantida, que está sempre classificada. Por exemplo, a parte inferior de uma matriz é mantida para ser classificada. Um elemento que deve ser 'inserido' nesta sub-lista ordenada, tem que encontrar seu lugar apropriado e então tem que ser inserido lá. Daí o nome,insertion sort.

A matriz é pesquisada sequencialmente e os itens não classificados são movidos e inseridos na sub-lista classificada (na mesma matriz). Este algoritmo não é adequado para grandes conjuntos de dados, pois sua complexidade média e de pior caso são de Ο (n ² ), onden é o número de itens.

Como funciona a classificação por inserção?

Pegamos um array não classificado como nosso exemplo.

A classificação por inserção compara os dois primeiros elementos.

Ele descobre que 14 e 33 já estão em ordem crescente. Por enquanto, 14 está na sub-lista classificada.

A classificação por inserção avança e compara 33 com 27.

E descobre que 33 não está na posição correta.

Ele troca 33 por 27. Ele também verifica todos os elementos da sub-lista classificada. Aqui, vemos que a sub-lista classificada tem apenas um elemento 14 e 27 é maior que 14. Portanto, a sub-lista classificada permanece classificada após a troca.

Agora temos 14 e 27 na sub-lista classificada. Em seguida, compara 33 com 10.

Esses valores não estão em uma ordem de classificação.

Então, nós os trocamos.

No entanto, a troca torna 27 e 10 não classificados.

Portanto, nós os trocamos também.

Novamente encontramos 14 e 10 em uma ordem não classificada.

Nós os trocamos novamente. No final da terceira iteração, temos uma sub-lista classificada de 4 itens.

Esse processo continua até que todos os valores não classificados sejam incluídos em uma sub-lista classificada. Agora veremos alguns aspectos de programação da classificação por inserção.

Algoritmo

Agora temos uma visão maior de como essa técnica de classificação funciona, para que possamos derivar etapas simples pelas quais podemos alcançar a classificação por inserção.

Step 1 − If it is the first element, it is already sorted. return 1;
Step 2 − Pick next element
Step 3 − Compare with all elements in the sorted sub-list
Step 4 − Shift all the elements in the sorted sub-list that is greater than the 
         value to be sorted
Step 5 − Insert the value
Step 6 − Repeat until list is sorted

Pseudo-código

procedure insertionSort( A : array of items )
   int holePosition
   int valueToInsert
	
   for i = 1 to length(A) inclusive do:
	
      /* select value to be inserted */
      valueToInsert = A[i]
      holePosition = i
      
      /*locate hole position for the element to be inserted */
		
      while holePosition > 0 and A[holePosition-1] > valueToInsert do:
         A[holePosition] = A[holePosition-1]
         holePosition = holePosition -1
      end while
		
      /* insert the number at hole position */
      A[holePosition] = valueToInsert
      
   end for
	
end procedure

Para saber sobre a implementação de classificação por inserção na linguagem de programação C, clique aqui .

A classificação por seleção é um algoritmo de classificação simples. Este algoritmo de classificação é um algoritmo baseado em comparação no local em que a lista é dividida em duas partes, a parte classificada na extremidade esquerda e a parte não classificada na extremidade direita. Inicialmente, a parte classificada está vazia e a parte não classificada é a lista inteira.

O menor elemento é selecionado na matriz não classificada e trocado pelo elemento mais à esquerda, e esse elemento se torna parte da matriz classificada. Este processo continua movendo o limite da matriz não classificada por um elemento à direita.

Este algoritmo não é adequado para grandes conjuntos de dados, pois sua complexidade média e pior caso são de Ο (n ² ), onden é o número de itens.

Como funciona a classificação por seleção?

Considere a seguinte matriz representada como exemplo.

Para a primeira posição na lista classificada, toda a lista é verificada sequencialmente. A primeira posição onde 14 está armazenado atualmente, pesquisamos em toda a lista e descobrimos que 10 é o valor mais baixo.

Portanto, substituímos 14 por 10. Após uma iteração 10, que por acaso é o valor mínimo da lista, aparece na primeira posição da lista classificada.

Para a segunda posição, onde 33 está residindo, começamos a examinar o resto da lista de maneira linear.

Descobrimos que 14 é o segundo valor mais baixo da lista e deve aparecer em segundo lugar. Trocamos esses valores.

Após duas iterações, dois valores mínimos são posicionados no início de maneira classificada.

O mesmo processo é aplicado ao restante dos itens da matriz.

A seguir está uma representação pictórica de todo o processo de classificação -

Agora, vamos aprender alguns aspectos de programação da classificação por seleção.

Algoritmo

Step 1 − Set MIN to location 0
Step 2 − Search the minimum element in the list
Step 3 − Swap with value at location MIN
Step 4 − Increment MIN to point to next element
Step 5 − Repeat until list is sorted

Pseudo-código

procedure selection sort 
   list  : array of items
   n     : size of list

   for i = 1 to n - 1
   /* set current element as minimum*/
      min = i    
  
      /* check the element to be minimum */

      for j = i+1 to n 
         if list[j] < list[min] then
            min = j;
         end if
      end for

      /* swap the minimum element with the current element*/
      if indexMin != i  then
         swap list[min] and list[i]
      end if
   end for
	
end procedure

Para saber sobre a implementação de classificação de seleção na linguagem de programação C, clique aqui .

A classificação por mesclagem é uma técnica de classificação baseada na técnica de divisão e conquista. Com o pior caso de complexidade de tempo sendo Ο (n log n), é um dos algoritmos mais respeitados.

A classificação por mesclagem primeiro divide a matriz em metades iguais e, a seguir, as combina de maneira classificada.

Como funciona a mesclagem de classificação?

Para entender a classificação por mesclagem, consideramos uma matriz não classificada como a seguir -

Sabemos que a classificação por mesclagem primeiro divide todo o array iterativamente em metades iguais, a menos que os valores atômicos sejam alcançados. Vemos aqui que um array de 8 itens é dividido em dois arrays de tamanho 4.

Isso não altera a sequência de aparência dos itens no original. Agora dividimos essas duas matrizes em metades.

Nós dividimos ainda mais essas matrizes e alcançamos o valor atômico que não pode mais ser dividido.

Agora, nós os combinamos exatamente da mesma maneira como foram divididos. Observe os códigos de cores dados a essas listas.

Primeiro comparamos o elemento de cada lista e, em seguida, os combinamos em outra lista de maneira classificada. Vemos que 14 e 33 estão em posições ordenadas. Comparamos 27 e 10 e na lista de destino de 2 valores colocamos 10 primeiro, seguido por 27. Alteramos a ordem de 19 e 35, enquanto 42 e 44 são colocados sequencialmente.

Na próxima iteração da fase de combinação, comparamos listas de dois valores de dados e os fundimos em uma lista de valores de dados encontrados, colocando todos em uma ordem de classificação.

Após a fusão final, a lista deve ficar assim -

Agora devemos aprender alguns aspectos de programação da classificação por mesclagem.

Algoritmo

A classificação por mesclagem continua dividindo a lista em metades iguais até que não possa mais ser dividida. Por definição, se for apenas um elemento da lista, ele é classificado. Em seguida, a classificação por mesclagem combina as listas menores classificadas mantendo a nova lista também classificada.

Step 1 − if it is only one element in the list it is already sorted, return.
Step 2 − divide the list recursively into two halves until it can no more be divided.
Step 3 − merge the smaller lists into new list in sorted order.

Pseudo-código

Veremos agora os pseudocódigos para funções de classificação por mesclagem. Como nossos algoritmos apontam duas funções principais - dividir e mesclar.

Merge sort funciona com recursão e veremos nossa implementação da mesma maneira.

procedure mergesort( var a as array )
   if ( n == 1 ) return a

   var l1 as array = a[0] ... a[n/2]
   var l2 as array = a[n/2+1] ... a[n]

   l1 = mergesort( l1 )
   l2 = mergesort( l2 )

   return merge( l1, l2 )
end procedure

procedure merge( var a as array, var b as array )

   var c as array
   while ( a and b have elements )
      if ( a[0] > b[0] )
         add b[0] to the end of c
         remove b[0] from b
      else
         add a[0] to the end of c
         remove a[0] from a
      end if
   end while
   
   while ( a has elements )
      add a[0] to the end of c
      remove a[0] from a
   end while
   
   while ( b has elements )
      add b[0] to the end of c
      remove b[0] from b
   end while
   
   return c
	
end procedure

Para saber mais sobre a implementação de merge sort na linguagem de programação C, clique aqui .

A classificação shell é um algoritmo de classificação altamente eficiente e é baseado no algoritmo de classificação por inserção. Este algoritmo evita grandes deslocamentos como no caso da classificação por inserção, se o valor menor estiver na extrema direita e tiver que ser movido na extrema esquerda.

Este algoritmo usa classificação por inserção em elementos amplamente espalhados, primeiro para classificá-los e, em seguida, classifica os elementos menos espaçados. Este espaçamento é denominado comointerval. Este intervalo é calculado com base na fórmula de Knuth como -

Fórmula de Knuth

h = h * 3 + 1
where −
   h is interval with initial value 1

Este algoritmo é bastante eficiente para conjuntos de dados de médio porte, pois sua complexidade média e de pior caso são de Ο (n), onde n é o número de itens.

Como funciona a classificação Shell?

Vamos considerar o exemplo a seguir para ter uma ideia de como funciona a classificação de shell. Pegamos o mesmo array que usamos em nossos exemplos anteriores. Para nosso exemplo e facilidade de compreensão, tomamos o intervalo de 4. Faça uma sub-lista virtual de todos os valores localizados no intervalo de 4 posições. Aqui, esses valores são {35, 14}, {33, 19}, {42, 27} e {10, 44}

Comparamos os valores em cada sub-lista e os trocamos (se necessário) no array original. Após esta etapa, a nova matriz deve se parecer com isto -

Então, pegamos o intervalo de 2 e essa lacuna gera duas sublistas - {14, 27, 35, 42}, {19, 10, 33, 44}

Comparamos e trocamos os valores, se necessário, na matriz original. Após esta etapa, a matriz deve ficar assim -

Por fim, classificamos o restante da matriz usando o intervalo de valor 1. A classificação por shell usa a classificação por inserção para classificar a matriz.

A seguir está a descrição passo a passo -

Vemos que foram necessárias apenas quatro trocas para classificar o restante do array.

Algoritmo

A seguir está o algoritmo para classificação de shell.

Step 1 − Initialize the value of h
Step 2 − Divide the list into smaller sub-list of equal interval h
Step 3 − Sort these sub-lists using insertion sort
Step 3 − Repeat until complete list is sorted

Pseudo-código

A seguir está o pseudocódigo para classificação de shell.

procedure shellSort()
   A : array of items 
	
   /* calculate interval*/
   while interval < A.length /3 do:
      interval = interval * 3 + 1	    
   end while
   
   while interval > 0 do:

      for outer = interval; outer < A.length; outer ++ do:

      /* select value to be inserted */
      valueToInsert = A[outer]
      inner = outer;

         /*shift element towards right*/
         while inner > interval -1 && A[inner - interval] >= valueToInsert do:
            A[inner] = A[inner - interval]
            inner = inner - interval
         end while

      /* insert the number at hole position */
      A[inner] = valueToInsert

      end for

   /* calculate interval*/
   interval = (interval -1) /3;	  

   end while
   
end procedure

Para saber sobre a implementação de classificação de shell na linguagem de programação C, clique aqui .

Fórmula de Knuth

h = h * 3 + 1
where −
   h is interval with initial value 1

Este algoritmo é bastante eficiente para conjuntos de dados de tamanho médio, pois sua complexidade média e de pior caso desse algoritmo depende da sequência de lacunas mais conhecida é Ο (n), onde n é o número de itens. E o pior caso de complexidade de espaço é O (n).

Como funciona a classificação Shell?

Comparamos os valores em cada sub-lista e os trocamos (se necessário) no array original. Após esta etapa, a nova matriz deve se parecer com isto -

Então, pegamos o intervalo de 1 e essa lacuna gera duas sublistas - {14, 27, 35, 42}, {19, 10, 33, 44}

Comparamos e trocamos os valores, se necessário, na matriz original. Após esta etapa, a matriz deve ficar assim -

Por fim, classificamos o restante da matriz usando o intervalo de valor 1. A classificação por shell usa a classificação por inserção para classificar a matriz.

A seguir está a descrição passo a passo -

Vemos que foram necessárias apenas quatro trocas para classificar o restante do array.

Algoritmo

A seguir está o algoritmo para classificação de shell.

Step 1 − Initialize the value of h
Step 2 − Divide the list into smaller sub-list of equal interval h
Step 3 − Sort these sub-lists using insertion sort
Step 3 − Repeat until complete list is sorted

Pseudo-código

A seguir está o pseudocódigo para classificação de shell.

procedure shellSort()
   A : array of items 
	
   /* calculate interval*/
   while interval < A.length /3 do:
      interval = interval * 3 + 1	    
   end while
   
   while interval > 0 do:

      for outer = interval; outer < A.length; outer ++ do:

      /* select value to be inserted */
      valueToInsert = A[outer]
      inner = outer;

         /*shift element towards right*/
         while inner > interval -1 && A[inner - interval] >= valueToInsert do:
            A[inner] = A[inner - interval]
            inner = inner - interval
         end while

      /* insert the number at hole position */
      A[inner] = valueToInsert

      end for

   /* calculate interval*/
   interval = (interval -1) /3;	  

   end while
   
end procedure

Para saber sobre a implementação de classificação de shell na linguagem de programação C, clique aqui .

A classificação rápida é um algoritmo de classificação altamente eficiente e se baseia no particionamento de uma matriz de dados em matrizes menores. Um grande array é particionado em dois arrays, um dos quais contém valores menores que o valor especificado, digamos pivô, com base no qual a partição é feita e outro array mantém valores maiores que o valor do pivô.

O Quicksort particiona um array e, em seguida, chama a si mesmo recursivamente duas vezes para classificar os dois subarrays resultantes. Esse algoritmo é bastante eficiente para conjuntos de dados de grande porte, pois sua complexidade média e de pior caso são O (nLogn) e image.png (n ² ), respectivamente.

Partição em classificação rápida

A representação animada a seguir explica como encontrar o valor pivô em uma matriz.

O valor pivô divide a lista em duas partes. E recursivamente, encontramos o pivô para cada sublista até que todas as listas contenham apenas um elemento.

Algoritmo de Pivô de Classificação Rápida

Com base em nosso entendimento de particionamento em classificação rápida, agora tentaremos escrever um algoritmo para ele, que é o seguinte.

Step 1 − Choose the highest index value has pivot
Step 2 − Take two variables to point left and right of the list excluding pivot
Step 3 − left points to the low index
Step 4 − right points to the high
Step 5 − while value at left is less than pivot move right
Step 6 − while value at right is greater than pivot move left
Step 7 − if both step 5 and step 6 does not match swap left and right
Step 8 − if left ≥ right, the point where they met is new pivot

Pseudocódigo de Pivô de Classificação Rápida

O pseudocódigo para o algoritmo acima pode ser derivado como -

function partitionFunc(left, right, pivot)
   leftPointer = left
   rightPointer = right - 1

   while True do
      while A[++leftPointer] < pivot do
         //do-nothing            
      end while
		
      while rightPointer > 0 && A[--rightPointer] > pivot do
         //do-nothing         
      end while
		
      if leftPointer >= rightPointer
         break
      else                
         swap leftPointer,rightPointer
      end if
		
   end while 
	
   swap leftPointer,right
   return leftPointer
	
end function

Algoritmo de classificação rápida

Usando o algoritmo de pivô recursivamente, acabamos com partições menores possíveis. Cada partição é então processada para classificação rápida. Definimos algoritmo recursivo para quicksort da seguinte forma -

Step 1 − Make the right-most index value pivot
Step 2 − partition the array using pivot value
Step 3 − quicksort left partition recursively
Step 4 − quicksort right partition recursively

Pseudocódigo de classificação rápida

Para obter mais informações, vamos ver o pseudocódigo para algoritmo de classificação rápida -

procedure quickSort(left, right)

   if right-left <= 0
      return
   else     
      pivot = A[right]
      partition = partitionFunc(left, right, pivot)
      quickSort(left,partition-1)
      quickSort(partition+1,right)    
   end if		
   
end procedure

Para saber sobre a implementação de classificação rápida na linguagem de programação C, clique aqui .

Um gráfico é uma representação pictórica de um conjunto de objetos onde alguns pares de objetos são conectados por links. Os objetos interconectados são representados por pontos denominados comovertices, e os links que conectam os vértices são chamados edges.

Formalmente, um gráfico é um par de conjuntos (V, E), Onde V é o conjunto de vértices e Eé o conjunto de arestas, conectando os pares de vértices. Dê uma olhada no gráfico a seguir -

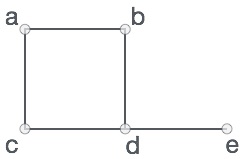
No gráfico acima,

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

Estrutura de dados do gráfico

Os gráficos matemáticos podem ser representados na estrutura de dados. Podemos representar um gráfico usando uma matriz de vértices e uma matriz bidimensional de arestas. Antes de prosseguirmos, vamos nos familiarizar com alguns termos importantes -

Vertex- Cada nó do gráfico é representado como um vértice. No exemplo a seguir, o círculo rotulado representa vértices. Assim, A a G são vértices. Podemos representá-los usando um array, conforme mostrado na imagem a seguir. Aqui, A pode ser identificado pelo índice 0. B pode ser identificado usando o índice 1 e assim por diante.
Edge- Edge representa um caminho entre dois vértices ou uma linha entre dois vértices. No exemplo a seguir, as linhas de A a B, B a C e assim por diante representam as arestas. Podemos usar um array bidimensional para representar um array conforme mostrado na imagem a seguir. Aqui AB pode ser representado como 1 na linha 0, coluna 1, BC como 1 na linha 1, coluna 2 e assim por diante, mantendo as outras combinações como 0.
Adjacency- Dois nós ou vértices são adjacentes se estiverem conectados um ao outro por meio de uma aresta. No exemplo a seguir, B é adjacente a A, C é adjacente a B e assim por diante.
Path- O caminho representa uma sequência de arestas entre os dois vértices. No exemplo a seguir, ABCD representa um caminho de A a D.

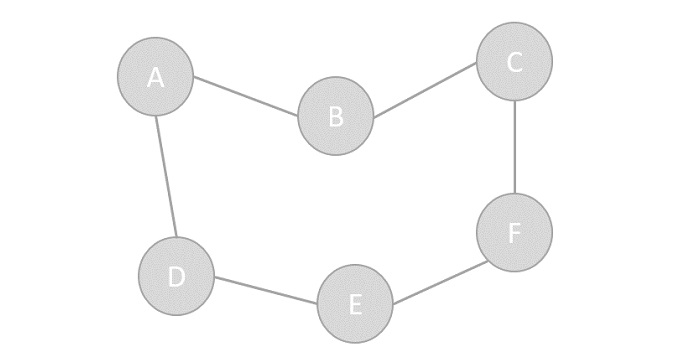
Operações básicas

A seguir estão as operações básicas básicas de um gráfico -

Add Vertex - Adiciona um vértice ao gráfico.
Add Edge - Adiciona uma aresta entre os dois vértices do gráfico.
Display Vertex - Exibe um vértice do gráfico.

Para saber mais sobre o Graph, leia o Tutorial da teoria do Graph . Aprenderemos como percorrer um gráfico nos próximos capítulos.

O algoritmo Depth First Search (DFS) percorre um gráfico em um movimento em profundidade e usa uma pilha para lembrar de obter o próximo vértice para iniciar uma pesquisa, quando um beco sem saída ocorre em qualquer iteração.

Como no exemplo dado acima, o algoritmo DFS atravessa de S para A para D para G para E para B primeiro, então para F e por último para C. Ele emprega as seguintes regras.

Rule 1- Visite o vértice não visitado adjacente. Marque como visitado. Mostre-o. Empurre-o em uma pilha.
Rule 2- Se nenhum vértice adjacente for encontrado, abra um vértice da pilha. (Irá aparecer todos os vértices da pilha, que não têm vértices adjacentes.)
Rule 3 - Repita a Regra 1 e a Regra 2 até que a pilha esteja vazia.

Degrau	Travessia	Descrição
1		Inicialize a pilha.
2		Marca Sconforme visitado e colocá-lo na pilha. Explore qualquer nó adjacente não visitado deS. Temos três nós e podemos escolher qualquer um deles. Para este exemplo, tomaremos o nó em ordem alfabética.
3		Marca Aconforme visitado e colocá-lo na pilha. Explore qualquer nó adjacente não visitado de A. AmbosS e D são adjacentes a A mas estamos preocupados apenas com nós não visitados.
4		Visita De marcá-lo como visitado e colocá-lo na pilha. Aqui temosB e C nós, que são adjacentes a De ambos não são visitados. No entanto, devemos escolher novamente em ordem alfabética.
5		Nós escolhemos B, marque-o como visitado e coloque-o na pilha. AquiBnão tem nenhum nó adjacente não visitado. Então, nós popB da pilha.
6		Verificamos o topo da pilha para retornar ao nó anterior e verificamos se há algum nó não visitado. Aqui encontramosD para estar no topo da pilha.
7		Apenas o nó adjacente não visitado é de D é Cagora. Então nós visitamosC, marque-o como visitado e coloque-o na pilha.

Como Cnão tem nenhum nó adjacente não visitado, portanto, continuamos aumentando a pilha até encontrar um nó que possui um nó adjacente não visitado. Nesse caso, não há nenhum e continuamos exibindo até que a pilha esteja vazia.

Para saber como é a implementação deste algoritmo na linguagem de programação C, clique aqui .

O algoritmo Breadth First Search (BFS) percorre um gráfico em um movimento de largura e usa uma fila para lembrar de obter o próximo vértice para iniciar uma pesquisa, quando um beco sem saída ocorre em qualquer iteração.

Como no exemplo dado acima, o algoritmo BFS atravessa de A para B para E para F primeiro, então para C e G por último para D. Ele emprega as seguintes regras.

Rule 1- Visite o vértice não visitado adjacente. Marque como visitado. Mostre-o. Insira-o em uma fila.
Rule 2 - Se nenhum vértice adjacente for encontrado, remova o primeiro vértice da fila.
Rule 3 - Repita a Regra 1 e a Regra 2 até que a fila esteja vazia.

Degrau	Travessia	Descrição
1		Inicialize a fila.
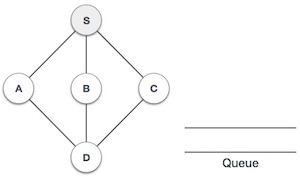
2		Começamos visitando S (nó inicial) e marque-o como visitado.
3		Em seguida, vemos um nó adjacente não visitado de S. Neste exemplo, temos três nós, mas em ordem alfabética, escolhemosA, marque-o como visitado e coloque-o na fila.
4		Em seguida, o nó adjacente não visitado de S é B. Nós o marcamos como visitado e o colocamos na fila.
5		Em seguida, o nó adjacente não visitado de S é C. Nós o marcamos como visitado e o colocamos na fila.
6		Agora, Sé deixado sem nós adjacentes não visitados. Então, retiramos da fila e encontramosA.
7		De A temos Dcomo nó adjacente não visitado. Nós o marcamos como visitado e o colocamos na fila.

Nesse estágio, não ficamos sem nós não marcados (não visitados). Mas, de acordo com o algoritmo, continuamos retirando a fila para obter todos os nós não visitados. Quando a fila se esvazia, o programa termina.

A implementação deste algoritmo em linguagem de programação C pode ser vista aqui .

A árvore representa os nós conectados por arestas. Discutiremos árvore binária ou árvore de pesquisa binária especificamente.

A árvore binária é uma estrutura de dados especial usada para fins de armazenamento de dados. Uma árvore binária tem uma condição especial de que cada nó pode ter no máximo dois filhos. Uma árvore binária tem os benefícios de uma matriz ordenada e uma lista vinculada, pois a pesquisa é tão rápida quanto em uma matriz classificada e as operações de inserção ou exclusão são tão rápidas quanto em uma lista vinculada.

Termos importantes

A seguir estão os termos importantes com respeito à árvore.

Path - Caminho refere-se à sequência de nós ao longo das bordas de uma árvore.
Root- O nó no topo da árvore é denominado raiz. Existe apenas uma raiz por árvore e um caminho do nó raiz para qualquer nó.
Parent - Qualquer nó, exceto o nó raiz, tem uma borda ascendente para um nó chamado pai.
Child - O nó abaixo de um determinado nó conectado por sua borda para baixo é chamado de nó filho.
Leaf - O nó que não possui nenhum nó filho é denominado nó folha.
Subtree - Subárvore representa os descendentes de um nó.
Visiting - A visita se refere à verificação do valor de um nó quando o controle está no nó.
Traversing - Traversing significa passar por nós em uma ordem específica.
Levels- O nível de um nó representa a geração de um nó. Se o nó raiz está no nível 0, então seu próximo nó filho está no nível 1, seu neto está no nível 2 e assim por diante.
keys - A chave representa um valor de um nó com base no qual uma operação de pesquisa deve ser realizada para um nó.

Representação da árvore de busca binária

A árvore de pesquisa binária exibe um comportamento especial. O filho esquerdo de um nó deve ter um valor menor que o valor de seu pai e o filho direito do nó deve ter um valor maior que seu valor pai.

Vamos implementar árvore usando objeto de nó e conectá-los por meio de referências.

Nó de Árvore

O código para escrever um nó de árvore seria semelhante ao que é fornecido a seguir. Ele tem uma parte de dados e referências a seus nós filho esquerdo e direito.

struct node {
   int data;   
   struct node *leftChild;
   struct node *rightChild;
};

Em uma árvore, todos os nós compartilham uma construção comum.

Operações básicas de BST

As operações básicas que podem ser realizadas em uma estrutura de dados de árvore de pesquisa binária são as seguintes -

Insert - Insere um elemento em uma árvore / cria uma árvore.
Search - Pesquisa um elemento em uma árvore.
Preorder Traversal - Atravessa uma árvore de forma pré-encomenda.
Inorder Traversal - Percorre uma árvore de maneira ordenada.
Postorder Traversal - Percorre uma árvore de maneira pós-ordem.

Devemos aprender a criar (inserir em) uma estrutura de árvore e pesquisar um item de dados em uma árvore neste capítulo. Aprenderemos sobre os métodos de travessia de árvores no próximo capítulo.

Operação de inserção

A primeira inserção cria a árvore. Depois, sempre que um elemento for inserido, primeiro localize seu local apropriado. Comece a pesquisar a partir do nó raiz e, em seguida, se os dados forem menores que o valor-chave, procure o local vazio na subárvore esquerda e insira os dados. Caso contrário, pesquise o local vazio na subárvore certa e insira os dados.

Algoritmo

If root is NULL 
   then create root node
return

If root exists then
   compare the data with node.data
   
   while until insertion position is located

      If data is greater than node.data
         goto right subtree
      else
         goto left subtree

   endwhile 
   
   insert data
	
end If

Implementação

A implementação da função de inserção deve ser semelhante a esta -

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty, create root node
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent  = NULL;

      while(1) {                
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }
			
         //go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}

Operação de Pesquisa

Sempre que um elemento deve ser pesquisado, comece a pesquisar a partir do nó raiz e, se os dados forem menores que o valor-chave, procure o elemento na subárvore esquerda. Caso contrário, pesquise o elemento na subárvore certa. Siga o mesmo algoritmo para cada nó.

Algoritmo

If root.data is equal to search.data
   return root
else
   while data not found

      If data is greater than node.data
         goto right subtree
      else
         goto left subtree
         
      If data found
         return node
   endwhile 
   
   return data not found
   
end if

A implementação desse algoritmo deve ser semelhante a esta.

struct node* search(int data) {
   struct node *current = root;
   printf("Visiting elements: ");

   while(current->data != data) {
      if(current != NULL)
      printf("%d ",current->data); 
      
      //go to left tree

      if(current->data > data) {
         current = current->leftChild;
      }
      //else go to right tree
      else {                
         current = current->rightChild;
      }

      //not found
      if(current == NULL) {
         return NULL;
      }

      return current;
   }  
}

Para saber sobre a implementação da estrutura de dados da árvore de pesquisa binária, clique aqui .

Traversal é um processo para visitar todos os nós de uma árvore e pode imprimir seus valores também. Porque, todos os nós são conectados por meio de arestas (links), sempre começamos a partir do nó raiz (cabeça). Ou seja, não podemos acessar aleatoriamente um nó em uma árvore. Existem três maneiras que usamos para atravessar uma árvore -

Transversal em ordem
Pré-encomendar Traversal
Traversal pós-pedido

Geralmente, percorremos uma árvore para pesquisar ou localizar um determinado item ou chave na árvore ou para imprimir todos os valores que ela contém.

Transversal em ordem

Neste método de travessia, a subárvore esquerda é visitada primeiro, depois a raiz e depois a subárvore direita. Devemos sempre lembrar que cada nó pode representar uma subárvore em si.

Se uma árvore binária for percorrida in-order, a saída produzirá valores-chave classificados em ordem crescente.

Nós começamos de A, e seguindo a travessia em ordem, nos movemos para sua subárvore esquerda B. Btambém é percorrido em ordem. O processo continua até que todos os nós sejam visitados. A saída da travessia em ordem desta árvore será -

D → B → E → A → F → C → G

Algoritmo

Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Visit root node.
Step 3 − Recursively traverse right subtree.

Pré-encomendar Traversal

Neste método de travessia, o nó raiz é visitado primeiro, depois a subárvore esquerda e finalmente a subárvore direita.

Nós começamos de Ae, após a travessia da pré-encomenda, visitamos primeiro A em si e, em seguida, mova para sua subárvore esquerda B. Btambém é percorrido na pré-encomenda. O processo continua até que todos os nós sejam visitados. O resultado da passagem de pré-encomenda desta árvore será -

A → B → D → E → C → F → G

Algoritmo

Until all nodes are traversed −
Step 1 − Visit root node.
Step 2 − Recursively traverse left subtree.
Step 3 − Recursively traverse right subtree.

Traversal pós-pedido

Neste método de passagem, o nó raiz é visitado por último, daí o nome. Primeiro, percorremos a subárvore esquerda, depois a subárvore direita e, finalmente, o nó raiz.

Nós começamos de A, e após a travessia de pós-pedido, primeiro visitamos a subárvore esquerda B. Btambém é percorrido pós-pedido. O processo continua até que todos os nós sejam visitados. A saída da travessia pós-pedido desta árvore será -

D → E → B → F → G → C → A

Algoritmo

Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Recursively traverse right subtree.
Step 3 − Visit root node.

Para verificar a implementação de travessia de árvore em C, clique aqui .

Uma árvore de pesquisa binária (BST) é uma árvore em que todos os nós seguem as propriedades mencionadas abaixo -

O valor da chave da subárvore esquerda é menor que o valor da chave de seu nó pai (raiz).
O valor da chave da subárvore direita é maior ou igual ao valor da chave de seu nó pai (raiz).

Assim, o BST divide todas as suas subárvores em dois segmentos; a subárvore esquerda e a subárvore direita e podem ser definidas como -

left_subtree (keys) < node (key) ≤ right_subtree (keys)

Representação

O BST é uma coleção de nós organizados de forma que mantenham as propriedades do BST. Cada nó possui uma chave e um valor associado. Durante a pesquisa, a chave desejada é comparada com as chaves no BST e, se encontrada, o valor associado é recuperado.

A seguir está uma representação pictórica do BST -

Observamos que a chave do nó raiz (27) possui todas as chaves de menor valor na subárvore esquerda e as chaves de maior valor na subárvore direita.

Operações básicas

A seguir estão as operações básicas de uma árvore -

Search - Pesquisa um elemento em uma árvore.
Insert - Insere um elemento em uma árvore.
Pre-order Traversal - Atravessa uma árvore de forma pré-encomenda.
In-order Traversal - Percorre uma árvore de maneira ordenada.
Post-order Traversal - Percorre uma árvore de maneira pós-ordem.

Nó

Defina um nó com alguns dados, referências a seus nós filhos esquerdo e direito.

struct node {
   int data;   
   struct node *leftChild;
   struct node *rightChild;
};

Operação de Pesquisa

Sempre que um elemento deve ser pesquisado, comece a pesquisar a partir do nó raiz. Então, se os dados forem menores que o valor da chave, procure o elemento na subárvore esquerda. Caso contrário, pesquise o elemento na subárvore certa. Siga o mesmo algoritmo para cada nó.

Algoritmo

struct node* search(int data){
   struct node *current = root;
   printf("Visiting elements: ");
	
   while(current->data != data){
	
      if(current != NULL) {
         printf("%d ",current->data);
			
         //go to left tree
         if(current->data > data){
            current = current->leftChild;
         }  //else go to right tree
         else {                
            current = current->rightChild;
         }
			
         //not found
         if(current == NULL){
            return NULL;
         }
      }			
   }
   
   return current;
}

Operação de inserção

Sempre que um elemento deve ser inserido, primeiro localize seu local apropriado. Comece a pesquisar a partir do nó raiz e, em seguida, se os dados forem menores que o valor-chave, procure o local vazio na subárvore esquerda e insira os dados. Caso contrário, pesquise o local vazio na subárvore certa e insira os dados.

Algoritmo

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;

      while(1) {                
         parent = current;
			
         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            //insert to the left
				
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }  //go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}

E se a entrada para a árvore de pesquisa binária vier de maneira classificada (crescente ou decrescente)? Ficará assim -

Observa-se que o desempenho de pior caso do BST é o mais próximo dos algoritmos de busca linear, ou seja, Ο (n). Em dados em tempo real, não podemos prever o padrão de dados e suas frequências. Assim, surge a necessidade de equilibrar o BST existente.

Nomeado após seu inventor Adelson, Velski E Landis, AVL treessão árvore de pesquisa binária de equilíbrio de altura. A árvore AVL verifica a altura das subárvores esquerda e direita e garante que a diferença não seja maior que 1. Esta diferença é chamada deBalance Factor.

Aqui, vemos que a primeira árvore está equilibrada e as duas próximas árvores não estão equilibradas -

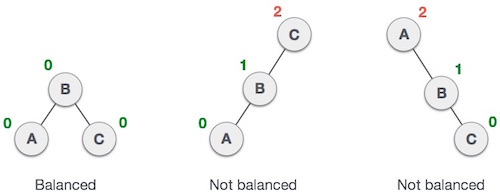
Na segunda árvore, a subárvore esquerda de C tem altura 2 e a subárvore direita tem altura 0, então a diferença é 2. Na terceira árvore, a subárvore direita de Atem altura 2 e falta a esquerda, então é 0 e a diferença é 2 novamente. A árvore AVL permite que a diferença (fator de equilíbrio) seja apenas 1.

BalanceFactor = height(left-sutree) − height(right-sutree)

Se a diferença na altura das subárvores esquerda e direita for maior que 1, a árvore é balanceada usando algumas técnicas de rotação.

Rotações AVL

Para se equilibrar, uma árvore AVL pode realizar os seguintes quatro tipos de rotações -

Rotação à esquerda
Rotação direita
Rotação esquerda-direita
Rotação direita-esquerda

As duas primeiras rotações são rotações simples e as duas rotações seguintes são rotações duplas. Para ter uma árvore desequilibrada, precisamos pelo menos de uma árvore de altura 2. Com esta árvore simples, vamos entendê-los um por um.

Rotação Esquerda

Se uma árvore se torna desequilibrada, quando um nó é inserido na subárvore direita da subárvore direita, então realizamos uma única rotação à esquerda -

Em nosso exemplo, nó Atornou-se desequilibrado porque um nó é inserido na subárvore direita da subárvore direita de A. Executamos a rotação para a esquerda, tornandoA a subárvore esquerda de B.

Rotação à Direita

A árvore AVL pode ficar desequilibrada, se um nó for inserido na subárvore esquerda da subárvore esquerda. A árvore então precisa de uma rotação correta.

Conforme representado, o nó desequilibrado se torna o filho direito de seu filho esquerdo executando uma rotação para a direita.

Rotação Esquerda-Direita

Rotações duplas são versões ligeiramente complexas de versões já explicadas de rotações. Para melhor entendê-los, devemos anotar cada ação realizada durante a rotação. Vamos primeiro verificar como realizar a rotação esquerda-direita. Uma rotação esquerda-direita é uma combinação de rotação esquerda seguida por rotação direita.

Estado	Açao
	Um nó foi inserido na subárvore direita da subárvore esquerda. Isto fazCum nó desequilibrado. Esses cenários fazem com que a árvore AVL execute a rotação da esquerda para a direita.
	Primeiro realizamos a rotação à esquerda na subárvore esquerda de C. Isto fazA, a subárvore esquerda de B.
	Nó C ainda está desequilibrado, porém agora, é por causa da subárvore esquerda da subárvore esquerda.
	Devemos agora girar a árvore para a direita, fazendo B o novo nó raiz desta subárvore. C agora se torna a subárvore direita de sua própria subárvore esquerda.
	A árvore agora está equilibrada.

Rotação direita-esquerda

O segundo tipo de rotação dupla é a rotação direita-esquerda. É uma combinação de rotação para a direita seguida de rotação para a esquerda.

Estado	Açao
	Um nó foi inserido na subárvore esquerda da subárvore direita. Isto fazA, um nó desequilibrado com fator de equilíbrio 2.
	Primeiro, fazemos a rotação correta ao longo C nó, fazendo C a subárvore direita de sua própria subárvore esquerda B. Agora,B torna-se a subárvore certa de A.
	Nó A ainda está desequilibrado por causa da subárvore direita de sua subárvore direita e requer uma rotação para a esquerda.
	Uma rotação para a esquerda é realizada fazendo B o novo nó raiz da subárvore. A torna-se a subárvore esquerda de sua subárvore direita B.
	A árvore agora está equilibrada.

Uma árvore geradora é um subconjunto do Gráfico G, que possui todos os vértices cobertos com o número mínimo possível de arestas. Portanto, uma árvore geradora não tem ciclos e não pode ser desconectada.

Por essa definição, podemos chegar à conclusão de que todo Grafo G conectado e não direcionado tem pelo menos uma árvore geradora. Um gráfico desconectado não possui nenhuma árvore estendida, pois não pode ser estendido a todos os seus vértices.

Encontramos três árvores abrangentes em um gráfico completo. Um gráfico não direcionado completo pode ter no máximon^n-2 número de árvores abrangentes, onde né o número de nós. No exemplo abordado acima,n is 3, conseqüentemente 3³⁻² = 3 árvores abrangentes são possíveis.

Propriedades Gerais de Spanning Tree

Agora entendemos que um gráfico pode ter mais de uma árvore de abrangência. A seguir estão algumas propriedades da árvore de abrangência conectada ao gráfico G -

Um grafo conectado G pode ter mais de uma árvore geradora.
Todas as árvores geradoras possíveis do grafo G têm o mesmo número de arestas e vértices.
A Spanning Tree não possui nenhum ciclo (loops).
Remover uma aresta da árvore de abrangência fará com que o gráfico se desconecte, ou seja, a árvore de abrangência é minimally connected.
Adicionar uma aresta à árvore geradora criará um circuito ou loop, ou seja, a árvore geradora é maximally acyclic.

Propriedades matemáticas da árvore de expansão

Spanning tree tem n-1 bordas, onde n é o número de nós (vértices).
De um gráfico completo, removendo o máximo e - n + 1 bordas, podemos construir uma árvore geradora.
Um gráfico completo pode ter no máximo n^n-2 número de árvores abrangentes.

Assim, podemos concluir que as árvores geradoras são um subconjunto do Gráfico G conectado e os gráficos desconectados não possuem árvore geradora.

Aplicação de Spanning Tree

Spanning tree é basicamente usado para encontrar um caminho mínimo para conectar todos os nós em um gráfico. A aplicação comum de árvores geradoras são -

Civil Network Planning
Computer Network Routing Protocol
Cluster Analysis

Vamos entender isso por meio de um pequeno exemplo. Considere a rede da cidade como um gráfico enorme e agora planeja implantar linhas telefônicas de forma que, no mínimo, possamos nos conectar a todos os nós da cidade. É aqui que a árvore de abrangência entra em cena.

Árvore de abrangência mínima (MST)

Em um gráfico ponderado, uma árvore de abrangência mínima é uma árvore de abrangência que tem peso mínimo do que todas as outras árvores de abrangência do mesmo gráfico. Em situações do mundo real, esse peso pode ser medido como distância, congestionamento, carga de tráfego ou qualquer valor arbitrário denotado nas bordas.

Algoritmo de árvore de abrangência mínima

Devemos aprender sobre dois algoritmos de árvore geradora mais importantes aqui -

Algoritmo de Kruskal
Algoritmo de Prim

Ambos são algoritmos gananciosos.

Heap é um caso especial de estrutura de dados de árvore binária balanceada, onde a chave do nó raiz é comparada com seus filhos e organizada de acordo. E seα tem nodo filho β então -

chave (α) ≥ chave (β)

Como o valor do pai é maior que o do filho, esta propriedade gera Max Heap. Com base nesses critérios, um heap pode ser de dois tipos -

For Input → 35 33 42 10 14 19 27 44 26 31

Min-Heap - Onde o valor do nó raiz é menor ou igual a qualquer um de seus filhos.

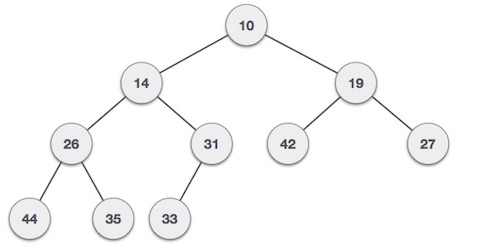
Max-Heap - Onde o valor do nó raiz é maior ou igual a qualquer um de seus filhos.

Ambas as árvores são construídas usando a mesma entrada e ordem de chegada.

Algoritmo de construção de pilha máxima

Devemos usar o mesmo exemplo para demonstrar como um Max Heap é criado. O procedimento para criar Min Heap é semelhante, mas optamos por valores mínimos em vez de valores máximos.

Vamos derivar um algoritmo para o heap máximo inserindo um elemento de cada vez. A qualquer momento, o heap deve manter sua propriedade. Durante a inserção, também assumimos que estamos inserindo um nó em uma árvore já montada.

Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.

Note - No algoritmo de construção Min Heap, esperamos que o valor do nó pai seja menor que o do nó filho.

Vamos entender a construção de Max Heap por uma ilustração animada. Consideramos a mesma amostra de entrada que usamos anteriormente.

Algoritmo de exclusão de heap máximo

Vamos derivar um algoritmo para excluir do heap máximo. A exclusão no heap máximo (ou mínimo) sempre ocorre na raiz para remover o valor máximo (ou mínimo).

Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.

Algumas linguagens de programação de computador permitem que um módulo ou função chame a si mesmo. Essa técnica é conhecida como recursão. Em recursão, uma funçãoα chama a si mesmo diretamente ou chama uma função β que por sua vez chama a função original α. A funçãoα é chamada de função recursiva.

Example - uma função que chama a si mesma.

int function(int value) {
   if(value < 1)
      return;
   function(value - 1);

   printf("%d ",value);   
}

Example - uma função que chama outra função que por sua vez a chama novamente.

int function1(int value1) {
   if(value1 < 1)
      return;
   function2(value1 - 1);
   printf("%d ",value1);   
}
int function2(int value2) {
   function1(value2);
}

Propriedades

Uma função recursiva pode ser infinita como um loop. Para evitar a execução infinita de função recursiva, existem duas propriedades que uma função recursiva deve ter -

Base criteria - Deve haver pelo menos um critério ou condição base, de modo que, quando essa condição for atendida, a função pare de chamar a si mesma recursivamente.
Progressive approach - As chamadas recursivas devem progredir de forma que cada vez que for feita uma chamada recursiva se aproxime dos critérios básicos.

Implementação

Muitas linguagens de programação implementam recursão por meio de stacks. Geralmente, sempre que uma função (caller) chama outra função (callee) ou ela própria como receptor, a função do chamador transfere o controle de execução para o receptor. Esse processo de transferência também pode envolver alguns dados a serem passados do chamador para o receptor.

Isso implica que a função do chamador deve suspender sua execução temporariamente e retomar mais tarde, quando o controle de execução retornar da função do receptor. Aqui, a função do chamador precisa começar exatamente do ponto de execução onde ela se coloca em espera. Ele também precisa dos mesmos valores de dados exatos nos quais estava trabalhando. Para tanto, é criado um registro de ativação (ou stack frame) para a função do chamador.

Este registro de ativação mantém as informações sobre variáveis locais, parâmetros formais, endereço de retorno e todas as informações passadas para a função do chamador.

Análise de recursão

Pode-se argumentar por que usar recursão, já que a mesma tarefa pode ser feita com iteração. A primeira razão é que a recursão torna um programa mais legível e, por causa dos sistemas de CPU aprimorados mais recentes, a recursão é mais eficiente do que as iterações.

Complexidade de tempo

No caso de iterações, consideramos o número de iterações para contar a complexidade do tempo. Da mesma forma, em caso de recursão, supondo que tudo seja constante, tentamos descobrir o número de vezes que uma chamada recursiva está sendo feita. Uma chamada feita para uma função é Ο (1), portanto, o (n) número de vezes que uma chamada recursiva é feita torna a função recursiva Ο (n).

Complexidade do Espaço

A complexidade do espaço é contabilizada como a quantidade de espaço extra necessária para a execução de um módulo. No caso de iterações, o compilador dificilmente requer qualquer espaço extra. O compilador continua atualizando os valores das variáveis usadas nas iterações. Mas em caso de recursão, o sistema precisa armazenar o registro de ativação cada vez que uma chamada recursiva é feita. Assim, considera-se que a complexidade espacial da função recursiva pode ser maior do que a de uma função com iteração.

Torre de Hanói, é um quebra-cabeça matemático que consiste em três torres (pinos) e mais de um anel é conforme representado -

Esses anéis são de tamanhos diferentes e empilhados em ordem crescente, ou seja, o menor fica sobre o maior. Existem outras variações do quebra-cabeça em que o número de discos aumenta, mas a contagem de torres permanece a mesma.

Regras

A missão é mover todos os discos para alguma outra torre sem violar a sequência de arranjo. Algumas regras a serem seguidas para a Torre de Hanói são -

Apenas um disco pode ser movido entre as torres a qualquer momento.
Apenas o disco "superior" pode ser removido.
Nenhum disco grande pode ficar sobre um disco pequeno.

A seguir está uma representação animada da resolução de um quebra-cabeça da Torre de Hanói com três discos.

O quebra-cabeça da Torre de Hanói com n discos pode ser resolvido no mínimo 2ⁿ−1passos. Esta apresentação mostra que um quebra-cabeça com 3 discos tomou2³ - 1 = 7 passos.

Algoritmo

Para escrever um algoritmo para Torre de Hanoi, primeiro precisamos aprender como resolver este problema com menor quantidade de discos, digamos → 1 ou 2. Marcamos três torres com o nome, source, destination e aux(apenas para ajudar a mover os discos). Se tivermos apenas um disco, ele pode ser facilmente movido do pino de origem para o destino.

Se tivermos 2 discos -

Primeiro, movemos o disco menor (superior) para aux Peg.
Em seguida, movemos o disco maior (inferior) para o pino de destino.
E, finalmente, movemos o disco menor do aux para o pino de destino.

Agora, estamos em posição de projetar um algoritmo para a Torre de Hanoi com mais de dois discos. Dividimos a pilha de discos em duas partes. O maior disco (n- ^ésimo disco) está em uma parte e todos os outros (n-1) discos estão na segunda parte.

Nosso objetivo final é mover o disco nda origem ao destino e coloque todos os outros discos (n1) nele. Podemos imaginar aplicar o mesmo de forma recursiva para todos os conjuntos de discos fornecidos.

Os passos a seguir são -

Step 1 − Move n-1 disks from source to aux
Step 2 − Move n^th disk from source to dest
Step 3 − Move n-1 disks from aux to dest

Um algoritmo recursivo para Torre de Hanói pode ser conduzido da seguinte maneira -

START
Procedure Hanoi(disk, source, dest, aux)

   IF disk == 1, THEN
      move disk from source to dest             
   ELSE
      Hanoi(disk - 1, source, aux, dest)     // Step 1
      move disk from source to dest          // Step 2
      Hanoi(disk - 1, aux, dest, source)     // Step 3
   END IF
   
END Procedure
STOP

Para verificar a implementação na programação C, clique aqui .

A série de Fibonacci gera o número subsequente adicionando dois números anteriores. A série de Fibonacci começa com dois números -F₀ & F₁. Os valores iniciais de F ₀ e F ₁ podem ser considerados 0, 1 ou 1, 1, respectivamente.

A série Fibonacci satisfaz as seguintes condições -

F_n = F_n-1 + F_n-2

Portanto, uma série de Fibonacci pode ter a seguinte aparência -

F ₈ = 0 1 1 2 3 5 8 13

ou, este -

F ₈ = 1 1 2 3 5 8 13 21

Para fins de ilustração, Fibonacci de F ₈ é exibido como -

Algoritmo Iterativo de Fibonacci

Primeiro, tentamos esboçar o algoritmo iterativo para a série de Fibonacci.

Procedure Fibonacci(n)
   declare f₀, f₁, fib, loop 
   
   set f₀ to 0
   set f₁ to 1
   
   display f₀, f₁
   
   for loop ← 1 to n
   
      fib ← f₀ + f₁   
      f₀ ← f₁
      f₁ ← fib

      display fib
   end for
	
end procedure

Para saber sobre a implementação do algoritmo acima na linguagem de programação C, clique aqui .

Algoritmo Recursivo de Fibonacci

Vamos aprender como criar um algoritmo recursivo da série de Fibonacci. Os critérios básicos de recursão.

START
Procedure Fibonacci(n)
   declare f₀, f₁, fib, loop 
   
   set f₀ to 0
   set f₁ to 1
   
   display f₀, f₁
   
   for loop ← 1 to n
   
      fib ← f₀ + f₁   
      f₀ ← f₁
      f₁ ← fib

      display fib
   end for

END

Para ver a implementação do algoritmo acima na linguagem de programação C, clique aqui .