Eletrônica de potência - Parâmetros de desempenho

É importante determinar os parâmetros de desempenho para diferentes conversores cujas topologias podem ser monofásicas ou multifásicas.

Suposições

• Os aparelhos utilizados são ideais, ou seja, não apresentam perdas
• Os dispositivos têm cargas resistivas

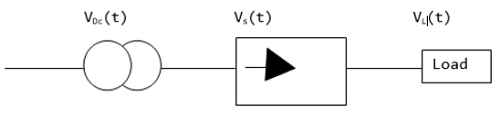
Tensão DC na carga

$$ V_ {DC} = \ frac {1} {T} \ int_ {0} ^ {T} V_ {L} \ left (t \ right) dt $$

Tensão RMS na carga

$$ V_ {L} = \ sqrt {\ frac {1} {T}} \ int_ {0} ^ {T} V_ {L} ^ {2} \ left (t \ right) dt $$

Fator de forma

$$ FF = \ frac {V_ {L}} {V_ {DC}} $$

Fator Ondulação

$$ RF = \ frac {\ sqrt {V_ {L} ^ {2} -V_ {DC} ^ {2}}} {V_ {DC}} = \ sqrt {FF ^ {2} -1} $$

Eficiência (fator de retificação)

$$ \ eta = \ frac {P_ {DC}} {P_ {L} + P_ {D}} $$

Onde o acima é definido como -

$ P_ {DC} = V_ {DC} \ vezes I_ {DC} $

$ P_ {L} = V_ {L} \ vezes I_ {L} $

$ P_ {D} = R_ {D} \ vezes I_ {L} ^ {2} $ ($ P_ {D} $ são as perdas do retificador e $ R_ {D} $ a resistência)

$$ \ eta = \ frac {V_ {DC} I_ {DC}} {\ left (V_ {L} I_ {L} \ right) + \ left (R_ {D} I_ {L} ^ {2} \ right )} = \ frac {V_ {DC} ^ {2}} {V_ {L} ^ {2}} \ times \ frac {1} {1+ \ frac {R_ {D}} {R_ {L}}} $$

Mas $ R_ {D} = 0 $

Portanto,

$$ \ eta = \ left (\ frac {V_ {DC}} {V_ {L}} \ right) ^ {2} = \ left (\ frac {1} {FF} \ right) ^ {2} $$

Fator de utilização do transformador

$$ TUF = \ frac {P_ {DC}} {VA \: Avaliação \: de \: o \: Transformador} = \ frac {P_ {DC}} {\ frac {VA_ {p} + VA_ {s}} {2}} $$

VA _p e VA _s são as classificações de potência primária e secundária do transformador.