Aprendizado profundo em Python - implementações

Nesta implementação de Deep learning, nosso objetivo é prever o atrito de clientes ou a rotatividade de dados de um determinado banco - quais clientes provavelmente deixarão este serviço bancário. O conjunto de dados usado é relativamente pequeno e contém 10.000 linhas com 14 colunas. Estamos usando a distribuição Anaconda e estruturas como Theano, TensorFlow e Keras. O Keras foi desenvolvido com base no Tensorflow e no Theano, que funcionam como back-ends.

# Artificial Neural Network
# Installing Theano
pip install --upgrade theano

# Installing Tensorflow
pip install –upgrade tensorflow

# Installing Keras
pip install --upgrade keras

Etapa 1: pré-processamento de dados

In[]:

# Importing the libraries
   import numpy as np
   import matplotlib.pyplot as plt
   import pandas as pd
 
# Importing the database
   dataset = pd.read_csv('Churn_Modelling.csv')

Passo 2

Criamos matrizes das características do conjunto de dados e da variável de destino, que é a coluna 14, rotulada como “Exited”.

A aparência inicial dos dados é mostrada abaixo -

In[]:
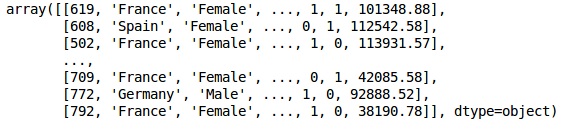
X = dataset.iloc[:, 3:13].values
Y = dataset.iloc[:, 13].values
X

Resultado

etapa 3

Resultado

array([1, 0, 1, ..., 1, 1, 0], dtype = int64)

Passo 4

Tornamos a análise mais simples codificando variáveis de string. Estamos usando a função ScikitLearn 'LabelEncoder' para codificar automaticamente os diferentes rótulos nas colunas com valores entre 0 e n_classes-1.

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder() 
X[:,1] = labelencoder_X_1.fit_transform(X[:,1]) 
labelencoder_X_2 = LabelEncoder() 
X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2])
X

Resultado

Na saída acima, os nomes dos países são substituídos por 0, 1 e 2; enquanto masculino e feminino são substituídos por 0 e 1.

Etapa 5

Labelling Encoded Data

Usamos o mesmo ScikitLearn biblioteca e outra função chamada de OneHotEncoder para apenas passar o número da coluna criando uma variável fictícia.

onehotencoder = OneHotEncoder(categorical features = [1])
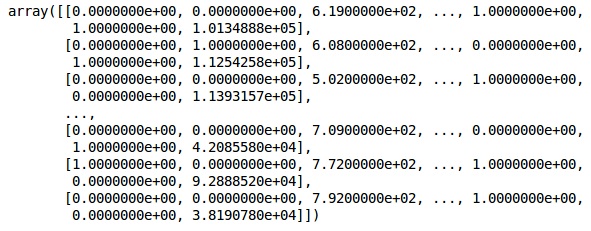
X = onehotencoder.fit_transform(X).toarray()
X = X[:, 1:]
X

Agora, as 2 primeiras colunas representam o país e a 4ª coluna representa o gênero.

Resultado

Sempre dividimos nossos dados em treinamento e teste; treinamos nosso modelo em dados de treinamento e depois verificamos a precisão de um modelo em dados de teste, o que ajuda a avaliar a eficiência do modelo.

Etapa 6

Estamos usando o ScikitLearn's train_test_splitfunção para dividir nossos dados em conjunto de treinamento e conjunto de teste. Mantemos a taxa de divisão do trem para o teste em 80:20.

#Splitting the dataset into the Training set and the Test Set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

Algumas variáveis têm valores em milhares, enquanto outras têm valores em dezenas ou unidades. Escalamos os dados para que sejam mais representativos.

Etapa 7

Neste código, estamos ajustando e transformando os dados de treinamento usando o StandardScalerfunção. Padronizamos nosso dimensionamento para usar o mesmo método ajustado para transformar / dimensionar os dados de teste.

# Feature Scaling

fromsklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)

Resultado

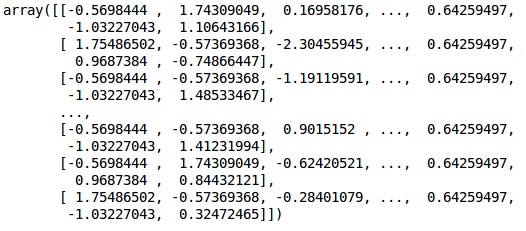
Os dados agora estão dimensionados corretamente. Finalmente, concluímos o nosso pré-processamento de dados. Agora, vamos começar com nosso modelo.

Etapa 8

Importamos os módulos necessários aqui. Precisamos do módulo Sequential para inicializar a rede neural e do módulo denso para adicionar as camadas ocultas.

# Importing the Keras libraries and packages 
import keras 
from keras.models import Sequential 
from keras.layers import Dense

Etapa 9

Chamaremos o modelo de Classificador, pois nosso objetivo é classificar a rotatividade de clientes. Em seguida, usamos o módulo Sequential para inicialização.

#Initializing Neural Network 
classifier = Sequential()

Etapa 10

Adicionamos as camadas ocultas uma a uma usando a função densa. No código abaixo, veremos muitos argumentos.

Nosso primeiro parâmetro é output_dim. É o número de nós que adicionamos a esta camada.inité a inicialização do Stochastic Gradient Decent. Em uma rede neural, atribuímos pesos a cada nó. Na inicialização, os pesos devem ser próximos a zero e nós inicializamos os pesos aleatoriamente usando a função uniforme. oinput_dimparâmetro é necessário apenas para a primeira camada, pois o modelo não conhece o número de nossas variáveis de entrada. Aqui, o número total de variáveis de entrada é 11. Na segunda camada, o modelo conhece automaticamente o número de variáveis de entrada da primeira camada oculta.

Execute a seguinte linha de código para adicionar a camada de entrada e a primeira camada oculta -

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu', input_dim = 11))

Execute a seguinte linha de código para adicionar a segunda camada oculta -

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu'))

Execute a seguinte linha de código para adicionar a camada de saída -

classifier.add(Dense(units = 1, kernel_initializer = 'uniform', 
activation = 'sigmoid'))

Etapa 11

Compiling the ANN

Nós adicionamos várias camadas ao nosso classificador até agora. Agora iremos compilá-los usando ocompilemétodo. Os argumentos adicionados no controle de compilação final completam a rede neural. Portanto, precisamos ter cuidado nesta etapa.

Aqui está uma breve explicação dos argumentos.

O primeiro argumento é Optimizer.Este é um algoritmo usado para encontrar o conjunto ideal de pesos. Este algoritmo é chamado deStochastic Gradient Descent (SGD). Aqui, estamos usando um entre vários tipos, chamado de 'otimizador Adam'. O SGD depende da perda, então nosso segundo parâmetro é perda. Se nossa variável dependente for binária, usamos a função de perda logarítmica chamada‘binary_crossentropy’, e se nossa variável dependente tiver mais de duas categorias na saída, então usamos ‘categorical_crossentropy’. Queremos melhorar o desempenho de nossa rede neural com base emaccuracy, então adicionamos metrics como precisão.

# Compiling Neural Network 
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

Etapa 12

Vários códigos precisam ser executados nesta etapa.

Ajustando a ANN ao Conjunto de Treinamento

Agora treinamos nosso modelo nos dados de treinamento. Nós usamos ofitmétodo para se ajustar ao nosso modelo. Também otimizamos os pesos para melhorar a eficiência do modelo. Para isso, temos que atualizar os pesos.Batch size é o número de observações após as quais atualizamos os pesos. Epoché o número total de iterações. Os valores de tamanho do lote e época são escolhidos pelo método de tentativa e erro.

classifier.fit(X_train, y_train, batch_size = 10, epochs = 50)

Fazendo previsões e avaliando o modelo

# Predicting the Test set results
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)

Prevendo uma única nova observação

# Predicting a single new observation
"""Our goal is to predict if the customer with the following data will leave the bank:
Geography: Spain
Credit Score: 500
Gender: Female
Age: 40
Tenure: 3
Balance: 50000
Number of Products: 2
Has Credit Card: Yes
Is Active Member: Yes

Etapa 13

Predicting the test set result

O resultado da previsão lhe dará a probabilidade de o cliente sair da empresa. Vamos converter essa probabilidade em binários 0 e 1.

# Predicting the Test set results 
y_pred = classifier.predict(X_test) 
y_pred = (y_pred > 0.5)

new_prediction = classifier.predict(sc.transform
(np.array([[0.0, 0, 500, 1, 40, 3, 50000, 2, 1, 1, 40000]])))
new_prediction = (new_prediction > 0.5)

Etapa 14

Esta é a última etapa em que avaliamos o desempenho do nosso modelo. Já temos resultados originais e, portanto, podemos construir uma matriz de confusão para verificar a precisão do nosso modelo.

Making the Confusion Matrix

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print (cm)

Resultado

loss: 0.3384 acc: 0.8605
[ [1541 54]
[230 175] ]

A partir da matriz de confusão, a precisão do nosso modelo pode ser calculada como -

Accuracy = 1541+175/2000=0.858

We achieved 85.8% accuracy, qual é bom.

O Algoritmo de Propagação Direta

Nesta seção, aprenderemos como escrever código para fazer propagação direta (predição) para uma rede neural simples -

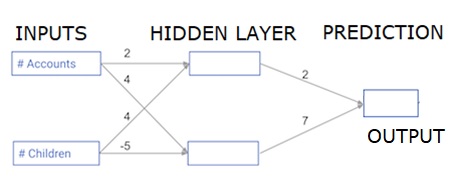
Cada ponto de dados é um cliente. A primeira entrada é quantas contas eles têm, e a segunda entrada é quantos filhos eles têm. O modelo irá prever quantas transações o usuário fará no próximo ano.

Os dados de entrada são pré-carregados como dados de entrada e os pesos estão em um dicionário chamado pesos. A matriz de pesos para o primeiro nó na camada oculta está em pesos ['nó_0'], e para o segundo nó na camada oculta estão em pesos ['nó_1'] respectivamente.

Os pesos que alimentam o nó de saída estão disponíveis em pesos.

A função de ativação linear retificada

Uma "função de ativação" é uma função que funciona em cada nó. Ele transforma a entrada do nó em alguma saída.

A função de ativação linear retificada (chamada ReLU ) é amplamente utilizada em redes de alto desempenho. Esta função recebe um único número como entrada, retornando 0 se a entrada for negativa e a entrada como saída se a entrada for positiva.

Aqui estão alguns exemplos -

relu (4) = 4
relu (-2) = 0

Preenchemos a definição da função relu () -

Usamos a função max () para calcular o valor da saída de relu ().
Aplicamos a função relu () a node_0_input para calcular node_0_output.
Aplicamos a função relu () a node_1_input para calcular node_1_output.

import numpy as np
input_data = np.array([-1, 2])
weights = {
   'node_0': np.array([3, 3]),
   'node_1': np.array([1, 5]),
   'output': np.array([2, -1])
}
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = np.tanh(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = np.tanh(node_1_input)
hidden_layer_output = np.array(node_0_output, node_1_output)
output =(hidden_layer_output * weights['output']).sum()
print(output)

def relu(input):
   '''Define your relu activation function here'''
   # Calculate the value for the output of the relu function: output
   output = max(input,0)
      # Return the value just calculated
   return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)

# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)

# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])

# Calculate model output (do not apply relu)
odel_output = (hidden_layer_outputs * weights['output']).sum()
print(model_output)# Print model output

Resultado

0.9950547536867305
-3

Aplicando a rede a muitas observações / linhas de dados

Nesta seção, aprenderemos como definir uma função chamada predict_with_network (). Esta função irá gerar previsões para múltiplas observações de dados, tomadas da rede acima, tomadas como dados_de_entrada. Os pesos dados na rede acima estão sendo usados. A definição da função relu () também está sendo usada.

Vamos definir uma função chamada predict_with_network () que aceita dois argumentos - input_data_row e pesos - e retorna uma previsão da rede como saída.

Calculamos os valores de entrada e saída para cada nó, armazenando-os como: node_0_input, node_0_output, node_1_input e node_1_output.

Para calcular o valor de entrada de um nó, multiplicamos as matrizes relevantes e calculamos sua soma.

Para calcular o valor de saída de um nó, aplicamos a função relu () ao valor de entrada do nó. Usamos um 'for loop' para iterar sobre input_data -

Também usamos nosso predict_with_network () para gerar previsões para cada linha do input_data - input_data_row. Também anexamos cada previsão aos resultados.

# Define predict_with_network()
def predict_with_network(input_data_row, weights):
   # Calculate node 0 value
   node_0_input = (input_data_row * weights['node_0']).sum()
   node_0_output = relu(node_0_input)
   
   # Calculate node 1 value
   node_1_input = (input_data_row * weights['node_1']).sum()
   node_1_output = relu(node_1_input)
   
   # Put node values into array: hidden_layer_outputs
   hidden_layer_outputs = np.array([node_0_output, node_1_output])
   
   # Calculate model output
   input_to_final_layer = (hidden_layer_outputs*weights['output']).sum()
   model_output = relu(input_to_final_layer)
# Return model output
   return(model_output)

# Create empty list to store prediction results
results = []
for input_data_row in input_data:
   # Append prediction to results
   results.append(predict_with_network(input_data_row, weights))
print(results)# Print results

Resultado

[0, 12]

Aqui, usamos a função relu onde relu (26) = 26 e relu (-13) = 0 e assim por diante.

Redes neurais multi-camadas profundas

Aqui, estamos escrevendo um código para fazer a propagação direta para uma rede neural com duas camadas ocultas. Cada camada oculta possui dois nós. Os dados de entrada foram pré-carregados comoinput_data. Os nós na primeira camada oculta são chamados de node_0_0 e node_0_1.

Seus pesos são pré-carregados como pesos ['node_0_0'] e pesos ['node_0_1'] respectivamente.

Os nós na segunda camada oculta são chamados node_1_0 and node_1_1. Seus pesos são pré-carregados comoweights['node_1_0'] e weights['node_1_1'] respectivamente.

Em seguida, criamos uma saída de modelo a partir dos nós ocultos usando pesos pré-carregados como weights['output'].

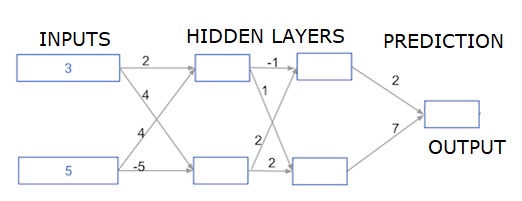
Calculamos node_0_0_input usando seus pesos, pesos ['node_0_0'] e os dados de entrada fornecidos. Em seguida, aplique a função relu () para obter node_0_0_output.

Fazemos o mesmo que acima para node_0_1_input para obter node_0_1_output.

Calculamos node_1_0_input usando seus pesos, pesos ['node_1_0'] e as saídas da primeira camada oculta - hidden_0_outputs. Em seguida, aplicamos a função relu () para obter node_1_0_output.

Fazemos o mesmo que acima para node_1_1_input para obter node_1_1_output.

Calculamos model_output usando pesos ['output'] e os outputs da segunda camada oculta, hidden_1_outputs array. Não aplicamos a função relu () a esta saída.

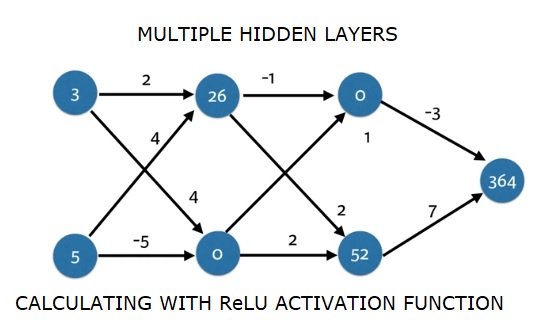
import numpy as np
input_data = np.array([3, 5])
weights = {
   'node_0_0': np.array([2, 4]),
   'node_0_1': np.array([4, -5]),
   'node_1_0': np.array([-1, 1]),
   'node_1_1': np.array([2, 2]),
   'output': np.array([2, 7])
}
def predict_with_network(input_data):
   # Calculate node 0 in the first hidden layer
   node_0_0_input = (input_data * weights['node_0_0']).sum()
   node_0_0_output = relu(node_0_0_input)
   
   # Calculate node 1 in the first hidden layer
   node_0_1_input = (input_data*weights['node_0_1']).sum()
   node_0_1_output = relu(node_0_1_input)
   
   # Put node values into array: hidden_0_outputs
   hidden_0_outputs = np.array([node_0_0_output, node_0_1_output])
   
   # Calculate node 0 in the second hidden layer
   node_1_0_input = (hidden_0_outputs*weights['node_1_0']).sum()
   node_1_0_output = relu(node_1_0_input)
   
   # Calculate node 1 in the second hidden layer
   node_1_1_input = (hidden_0_outputs*weights['node_1_1']).sum()
   node_1_1_output = relu(node_1_1_input)
   
   # Put node values into array: hidden_1_outputs
   hidden_1_outputs = np.array([node_1_0_output, node_1_1_output])
   
   # Calculate model output: model_output
   model_output = (hidden_1_outputs*weights['output']).sum()
      # Return model_output
   return(model_output)
output = predict_with_network(input_data)
print(output)

Resultado