Aprendizagem profunda em Python - Guia rápido

Aprendizagem estruturada profunda ou aprendizagem hierárquica ou aprendizagem profunda, em resumo, faz parte da família dos métodos de aprendizagem de máquina que são, eles próprios, um subconjunto do campo mais amplo da Inteligência Artificial.

O aprendizado profundo é uma classe de algoritmos de aprendizado de máquina que usa várias camadas de unidades de processamento não linear para extração e transformação de recursos. Cada camada sucessiva usa a saída da camada anterior como entrada.

Redes neurais profundas, redes de crenças profundas e redes neurais recorrentes foram aplicadas a campos como visão computacional, reconhecimento de fala, processamento de linguagem natural, reconhecimento de áudio, filtragem de rede social, tradução automática e bioinformática, onde produziram resultados comparáveis ​​e em alguns casos melhor do que os especialistas humanos.

Algoritmos e redes de aprendizado profundo -

• baseiam-se na aprendizagem não supervisionada de vários níveis de recursos ou representações dos dados. Recursos de nível superior são derivados de recursos de nível inferior para formar uma representação hierárquica.

• use alguma forma de descida gradiente para treinamento.

Neste capítulo, aprenderemos sobre o ambiente configurado para Python Deep Learning. Temos que instalar o seguinte software para fazer algoritmos de aprendizagem profunda.

• Python 2.7+
• Scipy com Numpy
• Matplotlib
• Theano
• Keras
• TensorFlow

É altamente recomendável que Python, NumPy, SciPy e Matplotlib sejam instalados por meio da distribuição Anaconda. Ele vem com todos esses pacotes.

Precisamos garantir que os diferentes tipos de software sejam instalados corretamente.

Vamos para o nosso programa de linha de comando e digite o seguinte comando -

$ python
Python 3.6.3 |Anaconda custom (32-bit)| (default, Oct 13 2017, 14:21:34)
[GCC 7.2.0] on linux

Em seguida, podemos importar as bibliotecas necessárias e imprimir suas versões -

import numpy
print numpy.__version__

Resultado

1.14.2

Instalação de Theano, TensorFlow e Keras

Antes de iniciarmos a instalação dos pacotes - Theano, TensorFlow e Keras, precisamos confirmar se o pipestá instalado. O sistema de gerenciamento de pacotes no Anaconda é chamado de pip.

Para confirmar a instalação do pip, digite o seguinte na linha de comando -

$ pip

Assim que a instalação do pip for confirmada, podemos instalar o TensorFlow e o Keras executando o seguinte comando -

$pip install theano $pip install tensorflow
$pip install keras

Confirme a instalação do Theano executando a seguinte linha de código -

$python –c “import theano: print (theano.__version__)”

Resultado

1.0.1

Confirme a instalação do Tensorflow executando a seguinte linha de código -

$python –c “import tensorflow: print tensorflow.__version__”

Resultado

1.7.0

Confirme a instalação do Keras executando a seguinte linha de código -

$python –c “import keras: print keras.__version__”
Using TensorFlow backend

Resultado

2.1.5

Inteligência Artificial (IA) é qualquer código, algoritmo ou técnica que permite a um computador imitar o comportamento ou inteligência cognitiva humana. O aprendizado de máquina (ML) é um subconjunto da IA ​​que usa métodos estatísticos para permitir que as máquinas aprendam e se aprimorem com a experiência. Deep Learning é um subconjunto do Machine Learning, o que torna viável o cálculo de redes neurais multicamadas. O aprendizado de máquina é visto como aprendizado superficial, enquanto o aprendizado profundo é visto como aprendizado hierárquico com abstração.

O aprendizado de máquina lida com uma ampla gama de conceitos. Os conceitos estão listados abaixo -

• supervised
• unsupervised
• aprendizagem por reforço
• regressão linear
• funções de custo
• overfitting
• under-fitting
• hiperparâmetro, etc.

No aprendizado supervisionado, aprendemos a prever valores a partir de dados rotulados. Uma técnica de ML que ajuda aqui é a classificação, em que os valores alvo são valores discretos; por exemplo, gatos e cachorros. Outra técnica de aprendizado de máquina que pode ajudar é a regressão. A regressão funciona nos valores alvo. Os valores alvo são valores contínuos; por exemplo, os dados do mercado de ações podem ser analisados ​​usando Regressão.

Na aprendizagem não supervisionada, fazemos inferências a partir dos dados de entrada que não são rotulados ou estruturados. Se temos um milhão de registros médicos e temos que dar sentido a isso, encontrar a estrutura subjacente, outliers ou detectar anomalias, usamos a técnica de agrupamento para dividir os dados em amplos clusters.

Os conjuntos de dados são divididos em conjuntos de treinamento, conjuntos de teste, conjuntos de validação e assim por diante.

Um avanço em 2012 trouxe o conceito de Deep Learning em destaque. Um algoritmo classificou 1 milhão de imagens em 1000 categorias usando 2 GPUs e tecnologias mais recentes como Big Data.

Relacionando o Deep Learning e o Machine Learning tradicional

Um dos principais desafios encontrados nos modelos tradicionais de aprendizado de máquina é um processo chamado extração de recursos. O programador precisa ser específico e informar ao computador os recursos a serem observados. Esses recursos ajudarão na tomada de decisões.

Inserir dados brutos no algoritmo raramente funciona, então a extração de recursos é uma parte crítica do fluxo de trabalho de aprendizado de máquina tradicional.

Isso coloca uma enorme responsabilidade sobre o programador, e a eficiência do algoritmo depende muito de quão inventivo o programador é. Para problemas complexos, como reconhecimento de objetos ou de escrita, esse é um grande problema.

O aprendizado profundo, com a capacidade de aprender várias camadas de representação, é um dos poucos métodos que nos ajuda na extração automática de recursos. Pode-se presumir que as camadas inferiores executam a extração automática de recursos, exigindo pouca ou nenhuma orientação do programador.

A Rede Neural Artificial, ou simplesmente rede neural para resumir, não é uma ideia nova. Já existe há cerca de 80 anos.

Foi só em 2011, quando Deep Neural Networks se tornou popular com o uso de novas técnicas, grande disponibilidade de conjuntos de dados e computadores poderosos.

Uma rede neural imita um neurônio, que tem dendritos, um núcleo, um axônio e um axônio terminal.

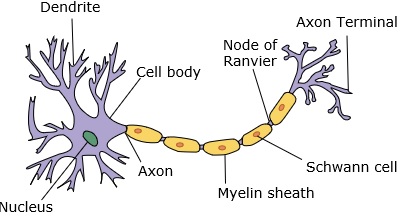
Para uma rede, precisamos de dois neurônios. Esses neurônios transferem informações por meio de sinapses entre os dendritos de um e o axônio terminal de outro.

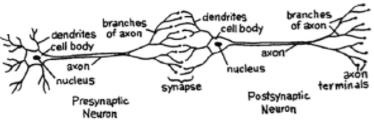
Um provável modelo de neurônio artificial se parece com isto -

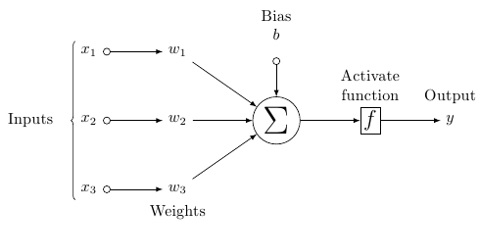
Uma rede neural será semelhante à mostrada abaixo -

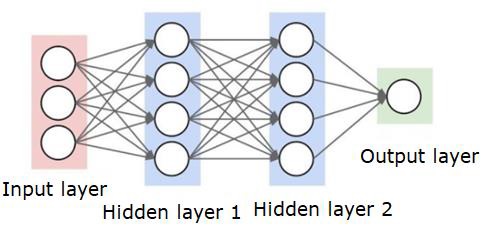
Os círculos são neurônios ou nós, com suas funções nos dados e as linhas / arestas que os conectam são os pesos / informações que estão sendo transmitidos.

Cada coluna é uma camada. A primeira camada de seus dados é a camada de entrada. Então, todas as camadas entre a camada de entrada e a camada de saída são as camadas ocultas.

Se você tiver uma ou algumas camadas ocultas, terá uma rede neural superficial. Se você tiver muitas camadas ocultas, terá uma rede neural profunda.

Nesse modelo, você tem dados de entrada, pondera-os e passa-os pela função no neurônio que é chamada de função de limiar ou função de ativação.

Basicamente, é a soma de todos os valores após a comparação com um determinado valor. Se você disparar um sinal, o resultado será (1) fora, ou nada será disparado, então (0). Isso é então pesado e passado para o próximo neurônio, e o mesmo tipo de função é executado.

Podemos ter uma função sigmóide (forma de s) como a função de ativação.

Quanto aos pesos, eles são apenas aleatórios para começar e são únicos por entrada no nó / neurônio.

Em um típico "feed forward", o tipo mais básico de rede neural, você faz com que suas informações sejam transmitidas diretamente pela rede que você criou e compara a saída com o que esperava que ela tivesse usando seus dados de amostra.

A partir daqui, você precisa ajustar os pesos para ajudá-lo a fazer com que sua saída corresponda à saída desejada.

O ato de enviar dados diretamente através de uma rede neural é chamado de feed forward neural network.

Nossos dados vão da entrada para as camadas, em ordem, e depois para a saída.

Quando voltamos e começamos a ajustar os pesos para minimizar a perda / custo, isso é chamado back propagation.

Isto é um optimization problem. Com a rede neural, na prática real, temos que lidar com centenas de milhares de variáveis, ou milhões, ou mais.

A primeira solução foi usar a descida gradiente estocástica como método de otimização. Agora, existem opções como AdaGrad, Adam Optimizer e assim por diante. De qualquer forma, esta é uma operação computacional massiva. É por isso que as redes neurais foram deixadas na prateleira por mais de meio século. Só muito recentemente é que tínhamos o poder e a arquitetura em nossas máquinas para sequer considerar a realização dessas operações, e os conjuntos de dados de tamanho adequado para corresponder.

Para tarefas de classificação simples, a rede neural tem desempenho relativamente próximo de outros algoritmos simples, como K vizinhos mais próximos. A real utilidade das redes neurais é percebida quando temos dados muito maiores e questões muito mais complexas, ambos os quais superam outros modelos de aprendizado de máquina.

Uma rede neural profunda (DNN) é uma RNA com várias camadas ocultas entre as camadas de entrada e saída. Semelhante a ANNs rasas, DNNs podem modelar relações não lineares complexas.

O objetivo principal de uma rede neural é receber um conjunto de entradas, realizar cálculos progressivamente complexos sobre elas e fornecer saídas para resolver problemas do mundo real, como classificação. Nós nos restringimos a alimentar redes neurais.

Temos uma entrada, uma saída e um fluxo de dados sequenciais em uma rede profunda.

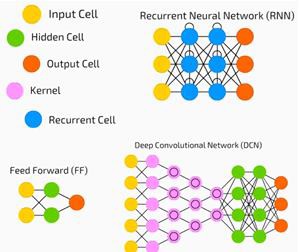
As redes neurais são amplamente utilizadas em problemas de aprendizagem supervisionada e aprendizagem por reforço. Essas redes são baseadas em um conjunto de camadas conectadas entre si.

No aprendizado profundo, o número de camadas ocultas, principalmente não lineares, pode ser grande; digamos cerca de 1000 camadas.

Os modelos DL produzem resultados muito melhores do que as redes ML normais.

Usamos principalmente o método gradiente descendente para otimizar a rede e minimizar a função de perda.

Podemos usar o Imagenet, um repositório de milhões de imagens digitais para classificar um conjunto de dados em categorias como cães e gatos. Redes DL são cada vez mais usadas para imagens dinâmicas, além das estáticas, e para séries temporais e análise de texto.

O treinamento dos conjuntos de dados é uma parte importante dos modelos de aprendizado profundo. Além disso, Backpropagation é o algoritmo principal no treinamento de modelos DL.

DL lida com o treinamento de grandes redes neurais com complexas transformações de entrada e saída.

Um exemplo de DL é o mapeamento de uma foto para o nome da (s) pessoa (s) na foto, como fazem nas redes sociais, e a descrição de uma imagem com uma frase é outra aplicação recente de DL.

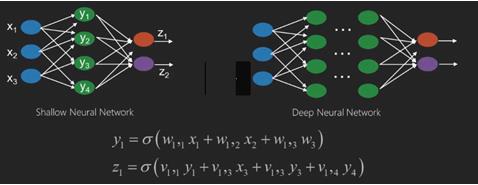
Redes neurais são funções que têm entradas como x1, x2, x3 ... que são transformadas em saídas como z1, z2, z3 e assim por diante em duas (redes rasas) ou várias operações intermediárias também chamadas de camadas (redes profundas).

Os pesos e vieses mudam de camada para camada. 'w' e 'v' são os pesos ou sinapses das camadas das redes neurais.

O melhor caso de uso de aprendizado profundo é o problema de aprendizado supervisionado. Aqui, temos um grande conjunto de entradas de dados com um conjunto desejado de saídas.

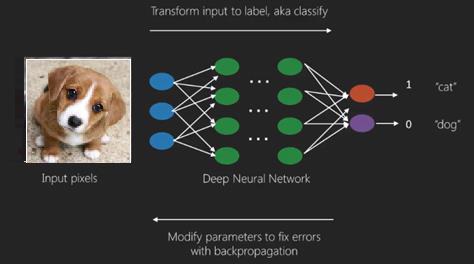
Aqui, aplicamos o algoritmo de propagação de retorno para obter a previsão de saída correta.

O conjunto de dados mais básico de aprendizado profundo é o MNIST, um conjunto de dados de dígitos escritos à mão.

Podemos treinar uma rede neural convolucional profunda com Keras para classificar imagens de dígitos manuscritos desse conjunto de dados.

O disparo ou ativação de um classificador de rede neural produz uma pontuação. Por exemplo, para classificar os pacientes como doentes e saudáveis, consideramos parâmetros como altura, peso e temperatura corporal, pressão arterial etc.

Uma pontuação alta significa que o paciente está doente e uma pontuação baixa significa que ele está saudável.

Cada nó na saída e camadas ocultas tem seus próprios classificadores. A camada de entrada pega entradas e passa suas pontuações para a próxima camada oculta para ativação posterior e isso continua até que a saída seja alcançada.

Este progresso da entrada para a saída da esquerda para a direita na direção para frente é chamado forward propagation.

Caminho de atribuição de crédito (CAP) em uma rede neural é a série de transformações começando da entrada para a saída. Os CAPs elaboram conexões causais prováveis ​​entre a entrada e a saída.

A profundidade do CAP para uma determinada rede neural feedforward ou a profundidade do CAP é o número de camadas ocultas mais uma à medida que a camada de saída é incluída. Para redes neurais recorrentes, onde um sinal pode se propagar através de uma camada várias vezes, a profundidade CAP pode ser potencialmente ilimitada.

Redes profundas e redes rasas

Não há um limite claro de profundidade que divida o aprendizado superficial do aprendizado profundo; mas é geralmente aceito que para o aprendizado profundo que tem várias camadas não lineares, o CAP deve ser maior do que dois.

O nó básico em uma rede neural é uma percepção que imita um neurônio em uma rede neural biológica. Então, temos Perception multicamadas ou MLP. Cada conjunto de entradas é modificado por um conjunto de pesos e tendências; cada aresta tem um peso único e cada nó tem uma tendência única.

A predição accuracy de uma rede neural depende de sua weights and biases.

O processo de melhoria da precisão da rede neural é chamado training. A saída de uma rede de suporte à frente é comparada com aquele valor que é conhecido como correto.

o cost function or the loss function é a diferença entre a saída gerada e a saída real.

O objetivo do treinamento é tornar o custo do treinamento o menor possível em milhões de exemplos de treinamento. Para fazer isso, a rede ajusta os pesos e tendências até que a previsão corresponda à saída correta.

Uma vez bem treinada, uma rede neural tem o potencial de fazer previsões precisas todas as vezes.

Quando o padrão se torna complexo e você deseja que o seu computador os reconheça, você deve escolher as redes neurais. Em tais cenários de padrões complexos, a rede neural supera todos os outros algoritmos concorrentes.

Agora existem GPUs que podem treiná-los mais rápido do que nunca. Redes neurais profundas já estão revolucionando o campo da IA

Os computadores provaram ser bons em realizar cálculos repetitivos e seguir instruções detalhadas, mas não foram tão bons em reconhecer padrões complexos.

Se houver o problema de reconhecimento de padrões simples, uma máquina de vetores de suporte (svm) ou um classificador de regressão logística podem fazer o trabalho bem, mas à medida que a complexidade do padrão aumenta, não há outra maneira senão ir para redes neurais profundas.

Portanto, para padrões complexos como um rosto humano, as redes neurais superficiais falham e não têm alternativa a não ser ir para redes neurais profundas com mais camadas. As redes profundas são capazes de fazer seu trabalho quebrando os padrões complexos em outros mais simples. Por exemplo, rosto humano; A rede adeep usaria bordas para detectar partes como lábios, nariz, olhos, orelhas e assim por diante e, em seguida, re-combiná-los para formar um rosto humano

A precisão da previsão correta tornou-se tão precisa que, recentemente, em um Desafio de reconhecimento de padrões do Google, uma rede profunda venceu um humano.

Essa ideia de uma teia de perceptrons em camadas existe há algum tempo; nesta área, as redes profundas imitam o cérebro humano. Mas uma desvantagem disso é que eles levam muito tempo para treinar, uma restrição de hardware

No entanto, as GPUs de alto desempenho recentes foram capazes de treinar essas redes profundas em menos de uma semana; enquanto os cpus rápidos poderiam ter levado semanas ou talvez meses para fazer o mesmo.

Escolhendo uma rede profunda

Como escolher uma rede profunda? Temos que decidir se estamos construindo um classificador ou se estamos tentando encontrar padrões nos dados e se vamos usar o aprendizado não supervisionado. Para extrair padrões de um conjunto de dados não rotulados, usamos uma máquina Boltzman restrita ou um codificador automático.

Considere os seguintes pontos ao escolher uma rede profunda -

• Para processamento de texto, análise de sentimento, análise sintática e reconhecimento de entidade de nome, usamos uma rede recorrente ou rede de tensor neural recursiva ou RNTN;

• Para qualquer modelo de linguagem que opere no nível do personagem, usamos a rede recorrente.

• Para reconhecimento de imagem, usamos a rede de crença profunda DBN ou rede convolucional.

• Para reconhecimento de objetos, usamos uma rede RNTN ou convolucional.

• Para reconhecimento de fala, usamos rede recorrente.

Em geral, redes de crença profunda e perceptrons multicamadas com unidades lineares retificadas ou RELU são boas escolhas para classificação.

Para análise de séries temporais, é sempre recomendado usar rede recorrente.

As redes neurais existem há mais de 50 anos; mas só agora eles ganharam destaque. A razão é que eles são difíceis de treinar; quando tentamos treiná-los com um método chamado retropropagação, nos deparamos com um problema chamado gradientes de desaparecimento ou explosão. Quando isso acontece, o treinamento leva mais tempo e a precisão fica para trás. Ao treinar um conjunto de dados, estamos constantemente calculando a função de custo, que é a diferença entre a saída prevista e a saída real de um conjunto de dados de treinamento rotulados. A função de custo é então minimizada ajustando os valores dos pesos e vieses até o valor mais baixo é obtido. O processo de treinamento usa um gradiente, que é a taxa na qual o custo mudará em relação à mudança no peso ou nos valores de polarização.

Redes restritas de Boltzman ou codificadores automáticos - RBNs

Em 2006, um avanço foi alcançado ao lidar com a questão dos gradientes de desaparecimento. Geoff Hinton concebeu uma nova estratégia que levou ao desenvolvimento deRestricted Boltzman Machine - RBM, uma rede rasa de duas camadas.

A primeira camada é a visible camada e a segunda camada é a hiddencamada. Cada nó da camada visível está conectado a todos os nós da camada oculta. A rede é conhecida como restrita, pois duas camadas dentro da mesma camada não têm permissão para compartilhar uma conexão.

Autoencoders são redes que codificam dados de entrada como vetores. Eles criam uma representação oculta ou compactada dos dados brutos. Os vetores são úteis na redução de dimensionalidade; o vetor compacta os dados brutos em um número menor de dimensões essenciais. Autoencoders são combinados com decodificadores, o que permite a reconstrução dos dados de entrada com base em sua representação oculta.

RBM é o equivalente matemático de um tradutor bidirecional. Uma passagem para frente pega as entradas e as traduz em um conjunto de números que codifica as entradas. Enquanto isso, uma passagem para trás pega esse conjunto de números e os converte de volta em entradas reconstruídas. Uma rede bem treinada executa a sustentação das costas com um alto grau de precisão.

Em qualquer uma das etapas, os pesos e os vieses têm um papel crítico; eles ajudam o RBM na decodificação das inter-relações entre as entradas e na decisão de quais entradas são essenciais na detecção de padrões. Por meio de passes para frente e para trás, o RBM é treinado para reconstruir a entrada com diferentes pesos e tendências até que a entrada e a construção sejam o mais próximo possível. Um aspecto interessante do RBM é que os dados não precisam ser rotulados. Isso acaba sendo muito importante para conjuntos de dados do mundo real, como fotos, vídeos, vozes e dados de sensores, todos os quais tendem a ser sem rótulos. Em vez de rotular manualmente os dados por humanos, o RBM classifica automaticamente os dados; ao ajustar adequadamente os pesos e vieses, um RBM é capaz de extrair características importantes e reconstruir a entrada. RBM é uma parte da família de redes neurais extratoras de recursos, que são projetadas para reconhecer padrões inerentes aos dados. Eles também são chamados de codificadores automáticos porque precisam codificar sua própria estrutura.

Deep Belief Networks - DBNs

Redes de crença profunda (DBNs) são formadas combinando RBMs e introduzindo um método de treinamento inteligente. Temos um novo modelo que finalmente resolve o problema do gradiente de desaparecimento. Geoff Hinton inventou os RBMs e também Deep Belief Nets como alternativa à propagação reversa.

Um DBN é semelhante em estrutura a um MLP (perceptron multicamadas), mas muito diferente quando se trata de treinamento. é o treinamento que permite que os DBNs superem seus equivalentes superficiais

Um DBN pode ser visualizado como uma pilha de RBMs onde a camada oculta de um RBM é a camada visível do RBM acima dele. O primeiro RBM é treinado para reconstruir sua entrada com a maior precisão possível.

A camada oculta do primeiro RBM é considerada a camada visível do segundo RBM e o segundo RBM é treinado usando as saídas do primeiro RBM. Esse processo é iterado até que todas as camadas da rede sejam treinadas.

Em um DBN, cada RBM aprende a entrada inteira. Um DBN funciona globalmente por meio do ajuste fino de toda a entrada em sucessão conforme o modelo melhora lentamente como uma lente de câmera lentamente focando uma imagem. Uma pilha de RBMs supera um único RBM, enquanto um perceptron MLP multi-camada supera um único perceptron.

Nesse estágio, os RBMs detectaram padrões inerentes aos dados, mas sem nenhum nome ou rótulo. Para finalizar o treinamento do DBN, temos que introduzir rótulos nos padrões e ajustar a rede com o aprendizado supervisionado.

Precisamos de um conjunto muito pequeno de amostras rotuladas para que os recursos e padrões possam ser associados a um nome. Este pequeno conjunto de dados rotulado é usado para treinamento. Este conjunto de dados rotulados pode ser muito pequeno quando comparado ao conjunto de dados original.

Os pesos e vieses são ligeiramente alterados, resultando em uma pequena mudança na percepção da rede dos padrões e freqüentemente um pequeno aumento na precisão total.

O treinamento também pode ser concluído em um período de tempo razoável usando GPUs, fornecendo resultados muito precisos em comparação com redes rasas e vemos uma solução para o problema do gradiente de desaparecimento também.

Redes Adversariais Generativas - GANs

As redes adversárias gerativas são redes neurais profundas que compreendem duas redes, colocadas uma contra a outra, daí o nome “adversário”.

Os GANs foram apresentados em um artigo publicado por pesquisadores da Universidade de Montreal em 2014. O especialista em IA do Facebook Yann LeCun, referindo-se aos GANs, chamou o treinamento adversarial de "a ideia mais interessante dos últimos 10 anos em ML".

O potencial das GANs é enorme, pois a varredura de rede aprende a imitar qualquer distribuição de dados. Os GANs podem ser ensinados a criar mundos paralelos notavelmente semelhantes ao nosso em qualquer domínio: imagens, música, fala, prosa. Eles são artistas de robôs de certa forma, e sua produção é bastante impressionante.

Em um GAN, uma rede neural, conhecida como gerador, gera novas instâncias de dados, enquanto a outra, o discriminador, avalia sua autenticidade.

Digamos que estejamos tentando gerar numerais escritos à mão, como aqueles encontrados no conjunto de dados MNIST, que são retirados do mundo real. O trabalho do discriminador, quando mostrado uma instância do verdadeiro conjunto de dados MNIST, é reconhecê-los como autênticos.

Agora considere as seguintes etapas do GAN -

• A rede do gerador recebe a entrada na forma de números aleatórios e retorna uma imagem.

• Esta imagem gerada é fornecida como entrada para a rede discriminadora junto com um fluxo de imagens tiradas do conjunto de dados real.

• O discriminador obtém imagens reais e falsas e retorna probabilidades, um número entre 0 e 1, com 1 representando uma previsão de autenticidade e 0 representando falsa.

• Então você tem um duplo ciclo de feedback -

  • O discriminador está em um loop de feedback com a verdade fundamental das imagens, que conhecemos.

  • O gerador está em um loop de feedback com o discriminador.

Redes Neurais Recorrentes - RNNs

RNNSare redes neurais nas quais os dados podem fluir em qualquer direção. Essas redes são usadas para aplicativos como modelagem de linguagem ou Processamento de Linguagem Natural (PNL).

O conceito básico subjacente aos RNNs é utilizar informações sequenciais. Em uma rede neural normal, assume-se que todas as entradas e saídas são independentes umas das outras. Se quisermos prever a próxima palavra em uma frase, precisamos saber quais palavras vieram antes dela.

Os RNNs são chamados de recorrentes, pois repetem a mesma tarefa para cada elemento de uma sequência, com a saída sendo baseada nos cálculos anteriores. Portanto, pode-se dizer que os RNNs têm uma “memória” que captura informações sobre o que foi calculado anteriormente. Em teoria, os RNNs podem usar informações em sequências muito longas, mas, na realidade, eles podem olhar para trás apenas algumas etapas.

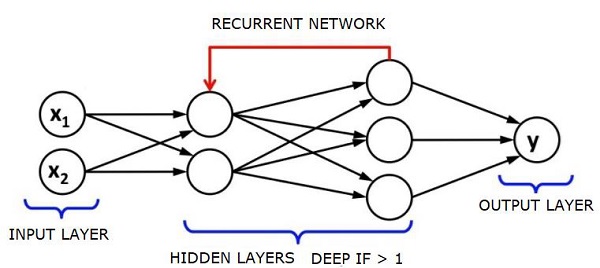
Redes de memória de longo prazo (LSTMs) são RNNs mais comumente usados.

Junto com redes neurais convolucionais, RNNs têm sido usados ​​como parte de um modelo para gerar descrições para imagens não marcadas. É incrível como isso parece funcionar bem.

Redes neurais convolucionais profundas - CNNs

Se aumentarmos o número de camadas em uma rede neural para torná-la mais profunda, isso aumentará a complexidade da rede e nos permitirá modelar funções que são mais complicadas. No entanto, o número de pesos e vieses aumentará exponencialmente. Na verdade, aprender esses problemas difíceis pode se tornar impossível para as redes neurais normais. Isso leva a uma solução, as redes neurais convolucionais.

As CNNs são amplamente utilizadas na visão computacional; têm sido aplicados também em modelagem acústica para reconhecimento automático de fala.

A ideia por trás das redes neurais convolucionais é a ideia de um “filtro móvel” que passa pela imagem. Este filtro móvel, ou convolução, se aplica a uma certa vizinhança de nós que por exemplo podem ser pixels, onde o filtro aplicado é 0,5 x o valor do nó -

O notável pesquisador Yann LeCun foi o pioneiro das redes neurais convolucionais. O Facebook, como software de reconhecimento facial, usa essas redes. A CNN tem sido a solução para projetos de visão de máquina. Existem muitas camadas em uma rede convolucional. No desafio Imagenet, uma máquina foi capaz de vencer um humano no reconhecimento de objetos em 2015.

Em suma, Redes Neurais Convolucionais (CNNs) são redes neurais multicamadas. As camadas às vezes chegam a 17 ou mais e supõem que os dados de entrada sejam imagens.

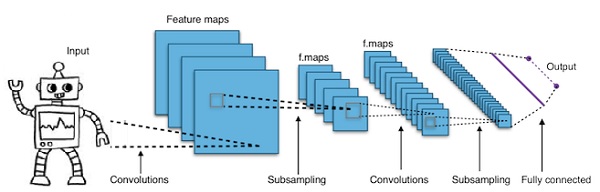
As CNNs reduzem drasticamente o número de parâmetros que precisam ser ajustados. Portanto, as CNNs lidam com eficiência com a alta dimensionalidade das imagens brutas.

Neste capítulo, veremos os fundamentos do Python Deep Learning.

Modelos / algoritmos de aprendizagem profunda

Vamos agora aprender sobre os diferentes modelos / algoritmos de aprendizado profundo.

Alguns dos modelos populares de aprendizagem profunda são os seguintes -

• Redes neurais convolucionais
• Redes neurais recorrentes
• Redes de crença profunda
• Redes adversárias geradoras
• Codificadores automáticos e assim por diante

As entradas e saídas são representadas como vetores ou tensores. Por exemplo, uma rede neural pode ter as entradas onde valores RGB de pixel individuais em uma imagem são representados como vetores.

As camadas de neurônios que ficam entre a camada de entrada e a camada de saída são chamadas de camadas ocultas. É aqui que a maior parte do trabalho acontece quando a rede neural tenta resolver problemas. Uma análise mais detalhada das camadas ocultas pode revelar muito sobre os recursos que a rede aprendeu a extrair dos dados.

Diferentes arquiteturas de redes neurais são formadas pela escolha de quais neurônios se conectar a outros neurônios na próxima camada.

Pseudocódigo para cálculo de saída

A seguir está o pseudocódigo para calcular a saída de Forward-propagating Neural Network -

• # node []: = array de nós classificados topologicamente
• # Uma aresta de a até b significa que a está à esquerda de b
• # Se a rede neural tiver entradas R e saídas S,
• # então os primeiros nós R são nós de entrada e os últimos nós S são nós de saída.
• # entrada [x]: = nós conectados ao nó x
• # peso [x]: = pesos das arestas de entrada para x

Para cada neurônio x, da esquerda para a direita -

• se x <= R: não fazer nada # é um nó de entrada
• entradas [x] = [saída [i] para i na entrada [x]]
• weighted_sum = dot_product (pesos [x], entradas [x])
• saída [x] = ativação_função (weighted_sum)

Agora aprenderemos como treinar uma rede neural. Também aprenderemos o algoritmo de propagação reversa e a passagem reversa no Python Deep Learning.

Temos que encontrar os valores ótimos dos pesos de uma rede neural para obter a saída desejada. Para treinar uma rede neural, usamos o método de descida gradiente iterativo. Começamos inicialmente com a inicialização aleatória dos pesos. Após a inicialização aleatória, fazemos previsões sobre algum subconjunto dos dados com o processo de propagação direta, calculamos a função de custo correspondente C e atualizamos cada peso w por um valor proporcional a dC / dw, ou seja, a derivada das funções de custo em relação ao peso. A constante de proporcionalidade é conhecida como taxa de aprendizado.

Os gradientes podem ser calculados de forma eficiente usando o algoritmo de retropropagação. A principal observação da propagação para trás ou prop para trás é que, por causa da regra da cadeia de diferenciação, o gradiente em cada neurônio na rede neural pode ser calculado usando o gradiente nos neurônios, ele tem bordas de saída para. Conseqüentemente, calculamos os gradientes de trás para frente, ou seja, primeiro calculamos os gradientes da camada de saída, depois a camada oculta mais acima, seguida pela camada oculta anterior e assim por diante, terminando na camada de entrada.

O algoritmo de retropropagação é implementado principalmente usando a ideia de um gráfico computacional, onde cada neurônio é expandido para vários nós no gráfico computacional e realiza uma operação matemática simples como adição, multiplicação. O gráfico computacional não tem pesos nas arestas; todos os pesos são atribuídos aos nós, então os pesos se tornam seus próprios nós. O algoritmo de propagação para trás é então executado no gráfico computacional. Assim que o cálculo for concluído, apenas os gradientes dos nós de peso são necessários para atualização. O resto dos gradientes podem ser descartados.

Técnica de Otimização de Gradiente Descendente

Uma função de otimização comumente usada que ajusta os pesos de acordo com o erro que eles causaram é chamada de "descida gradiente".

Gradiente é outro nome para inclinação, e inclinação, em um gráfico xy, representa como duas variáveis ​​estão relacionadas entre si: a subida sobre a corrida, a mudança na distância sobre a mudança no tempo, etc. Neste caso, a inclinação é a relação entre o erro da rede e um único peso; ou seja, como o erro muda conforme o peso varia.

Para ser mais preciso, queremos descobrir qual peso produz o menor erro. Queremos encontrar o peso que representa corretamente os sinais contidos nos dados de entrada e os traduz para uma classificação correta.

Conforme uma rede neural aprende, ela lentamente ajusta muitos pesos para que eles possam mapear o sinal para o significado corretamente. A razão entre o erro da rede e cada um desses pesos é uma derivada, dE / dw que calcula a extensão em que uma ligeira mudança em um peso causa uma ligeira mudança no erro.

Cada peso é apenas um fator em uma rede profunda que envolve muitas transformações; o sinal do peso passa por ativações e somas por várias camadas, portanto, usamos a regra da cadeia de cálculo para trabalhar de volta através das ativações e saídas da rede. Isso nos leva ao peso em questão e sua relação com o erro geral.

Dadas duas variáveis, erro e peso, são mediados por uma terceira variável, activation, através do qual o peso é passado. Podemos calcular como uma mudança no peso afeta uma mudança no erro, primeiro calculando como uma mudança na ativação afeta uma mudança no Erro, e como uma mudança no peso afeta uma mudança na ativação.

A ideia básica no aprendizado profundo nada mais é do que isso: ajustar os pesos de um modelo em resposta ao erro que ele produz, até que você não consiga mais reduzir o erro.

A rede profunda treina lentamente se o valor do gradiente for pequeno e rápido se o valor for alto. Quaisquer imprecisões no treinamento levam a resultados imprecisos. O processo de treinar as redes da saída de volta para a entrada é chamado de propagação reversa ou back prop. Sabemos que a propagação direta começa com a entrada e segue em frente. O suporte traseiro faz o inverso / oposto calculando o gradiente da direita para a esquerda.

Cada vez que calculamos um gradiente, usamos todos os gradientes anteriores até aquele ponto.

Vamos começar em um nó na camada de saída. A aresta usa o gradiente nesse nó. À medida que voltamos para as camadas ocultas, fica mais complexo. O produto de dois números entre 0 e 1 resulta em um número menor. O valor do gradiente fica cada vez menor e, como resultado, o suporte traseiro leva muito tempo para treinar e a precisão é prejudicada.

Desafios em algoritmos de aprendizado profundo

Existem certos desafios para redes neurais rasas e redes neurais profundas, como overfitting e tempo de computação. DNNs são afetados por overfitting devido ao uso de camadas adicionais de abstração que permitem modelar dependências raras nos dados de treinamento.

Regularizationmétodos como abandono escolar, parada precoce, aumento de dados e aprendizagem por transferência são aplicados durante o treinamento para combater o sobreajuste. A regularização de exclusão omite aleatoriamente unidades das camadas ocultas durante o treinamento, o que ajuda a evitar dependências raras. Os DNNs levam em consideração vários parâmetros de treinamento como o tamanho, ou seja, o número de camadas e o número de unidades por camada, a taxa de aprendizado e os pesos iniciais. Encontrar parâmetros ótimos nem sempre é prático devido ao alto custo em tempo e recursos computacionais. Vários hacks, como batching, podem acelerar a computação. O grande poder de processamento das GPUs ajudou significativamente o processo de treinamento, pois os cálculos matriciais e vetoriais necessários são bem executados nas GPUs.

Cair fora

Dropout é uma técnica de regularização popular para redes neurais. Redes neurais profundas são particularmente propensas a overfitting.

Vamos agora ver o que é o abandono e como funciona.

Nas palavras de Geoffrey Hinton, um dos pioneiros do Deep Learning, 'Se você tem uma rede neural profunda e ela não é overfitting, você provavelmente deveria usar uma maior e abandonar'.

Dropout é uma técnica em que, durante cada iteração de descida de gradiente, soltamos um conjunto de nós selecionados aleatoriamente. Isso significa que ignoramos alguns nós aleatoriamente como se eles não existissem.

Cada neurônio é mantido com uma probabilidade qe descartado aleatoriamente com probabilidade 1-q. O valor q pode ser diferente para cada camada da rede neural. Um valor de 0,5 para as camadas ocultas e 0 para a camada de entrada funciona bem em uma ampla gama de tarefas.

Durante a avaliação e previsão, nenhum dropout é usado. A saída de cada neurônio é multiplicada por q para que a entrada para a próxima camada tenha o mesmo valor esperado.

A ideia por trás do Dropout é a seguinte - em uma rede neural sem regularização de dropout, os neurônios desenvolvem co-dependência entre si, o que leva ao overfitting.

Truque de implementação

O dropout é implementado em bibliotecas como TensorFlow e Pytorch, mantendo a saída dos neurônios selecionados aleatoriamente como 0. Ou seja, embora o neurônio exista, sua saída é substituída como 0.

Parada Antecipada

Treinamos redes neurais usando um algoritmo iterativo chamado gradiente descendente.

A ideia por trás da parada precoce é intuitiva; paramos de treinar quando o erro começa a aumentar. Aqui, por erro, queremos dizer o erro medido nos dados de validação, que é a parte dos dados de treinamento usados ​​para ajustar hiperparâmetros. Nesse caso, o hiperparâmetro são os critérios de parada.

Aumento de dados

O processo em que aumentamos o quantum de dados que temos ou o aumentamos usando os dados existentes e aplicando algumas transformações neles. As transformações exatas usadas dependem da tarefa que pretendemos realizar. Além disso, as transformações que ajudam a rede neural dependem de sua arquitetura.

Por exemplo, em muitas tarefas de visão computacional, como classificação de objetos, uma técnica de aumento de dados eficaz é adicionar novos pontos de dados que são recortados ou versões traduzidas dos dados originais.

Quando um computador aceita uma imagem como entrada, ele obtém uma matriz de valores de pixel. Digamos que toda a imagem seja deslocada 15 pixels para a esquerda. Aplicamos muitas mudanças diferentes em direções diferentes, resultando em um conjunto de dados aumentado muitas vezes o tamanho do conjunto de dados original.

Aprendizagem por transferência

O processo de pegar um modelo pré-treinado e “ajustar” o modelo com nosso próprio conjunto de dados é chamado de aprendizagem por transferência. Existem várias maneiras de fazer isso. Algumas maneiras são descritas abaixo -

• Treinamos o modelo pré-treinado em um grande conjunto de dados. Em seguida, removemos a última camada da rede e a substituímos por uma nova camada com pesos aleatórios.

• Em seguida, congelamos os pesos de todas as outras camadas e treinamos a rede normalmente. Aqui, congelar as camadas não altera os pesos durante a descida ou otimização do gradiente.

O conceito por trás disso é que o modelo pré-treinado atuará como um extrator de recursos e apenas a última camada será treinada na tarefa atual.

A retropropagação é implementada em frameworks de aprendizado profundo como Tensorflow, Torch, Theano, etc., usando gráficos computacionais. Mais significativamente, entender a propagação de retorno em gráficos computacionais combina vários algoritmos diferentes e suas variações, como backprop através do tempo e backprop com pesos compartilhados. Depois que tudo é convertido em um gráfico computacional, eles ainda são o mesmo algoritmo - apenas propagação de volta em gráficos computacionais.

O que é gráfico computacional

Um gráfico computacional é definido como um gráfico direcionado onde os nós correspondem a operações matemáticas. Os gráficos computacionais são uma forma de expressar e avaliar uma expressão matemática.

Por exemplo, aqui está uma equação matemática simples -

$$p = x+y$$

Podemos desenhar um gráfico computacional da equação acima da seguinte maneira.

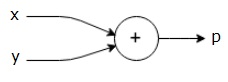
O gráfico computacional acima tem um nó de adição (nó com sinal "+") com duas variáveis ​​de entrada xey e uma saída q.

Tomemos outro exemplo, um pouco mais complexo. Temos a seguinte equação.

$$g = \left (x+y \right ) \ast z $$

A equação acima é representada pelo seguinte gráfico computacional.

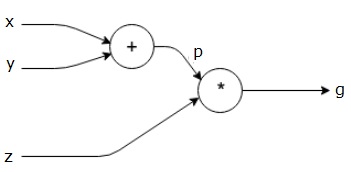
Gráficos computacionais e retropropagação

Gráficos computacionais e retropropagação, ambos são conceitos centrais importantes no aprendizado profundo para o treinamento de redes neurais.

Passar para a frente

A passagem para frente é o procedimento para avaliar o valor da expressão matemática representada por gráficos computacionais. Fazer a passagem direta significa que estamos passando o valor das variáveis ​​na direção direta da esquerda (entrada) para a direita onde está a saída.

Vamos considerar um exemplo dando algum valor a todas as entradas. Suponha que os seguintes valores sejam dados a todas as entradas.

$$x=1, y=3, z=−3$$

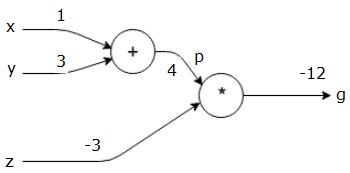
Ao fornecer esses valores às entradas, podemos realizar a passagem para frente e obter os seguintes valores para as saídas em cada nó.

Primeiro, usamos o valor de x = 1 ey = 3, para obter p = 4.

Então usamos p = 4 e z = -3 para obter g = -12. Vamos da esquerda para a direita, para a frente.

Objetivos do passe para trás

Na passagem para trás, nossa intenção é calcular os gradientes para cada entrada em relação à saída final. Esses gradientes são essenciais para treinar a rede neural usando gradiente descendente.

Por exemplo, desejamos os seguintes gradientes.

Gradientes desejados

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$

Passe para trás (retropropagação)

Começamos a passagem para trás encontrando a derivada da saída final em relação à saída final (em si!). Assim, resultará na derivação da identidade e o valor é igual a um.

$$\frac{\partial g}{\partial g} = 1$$

Nosso gráfico computacional agora se parece com o mostrado abaixo -

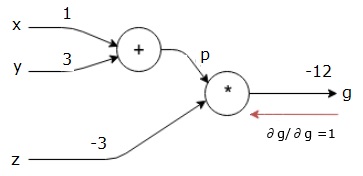
A seguir, faremos a passagem para trás por meio da operação "*". Vamos calcular os gradientes em pe z. Como g = p * z, sabemos que -

$$\frac{\partial g}{\partial z} = p$$

$$\frac{\partial g}{\partial p} = z$$

Já sabemos os valores de zep do passe para frente. Portanto, obtemos -

$$\frac{\partial g}{\partial z} = p = 4$$

e

$$\frac{\partial g}{\partial p} = z = -3$$

Queremos calcular os gradientes em x e y -

$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$

No entanto, queremos fazer isso de forma eficiente (embora xeg estejam a apenas dois saltos de distância neste gráfico, imagine-os realmente distantes um do outro). Para calcular esses valores de forma eficiente, usaremos a regra da cadeia de diferenciação. Da regra da cadeia, temos -

$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

Mas já sabemos que dg / dp = -3, dp / dx e dp / dy são fáceis, pois p depende diretamente de x e y. Nós temos -

$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$

Portanto, obtemos -

$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \right ).1 = -3$$

Além disso, para a entrada y -

$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \right ).1 = -3$$

A principal razão para fazer isso ao contrário é que quando tivemos que calcular o gradiente em x, usamos apenas valores já calculados e dq / dx (derivada da saída do nó em relação à entrada do mesmo nó). Usamos informações locais para calcular um valor global.

Etapas para treinar uma rede neural

Siga estas etapas para treinar uma rede neural -

• Para o ponto de dados x no conjunto de dados, fazemos a passagem direta com x como entrada e calculamos o custo c como saída.

• Fazemos o retrocesso começando em c, e calculamos gradientes para todos os nós no gráfico. Isso inclui nós que representam os pesos da rede neural.

• Em seguida, atualizamos os pesos fazendo W = W - gradientes da taxa de aprendizagem.

• Repetimos esse processo até que os critérios de parada sejam atendidos.

O aprendizado profundo produziu bons resultados para algumas aplicações, como visão computacional, tradução de linguagem, legendagem de imagens, transcrição de áudio, biologia molecular, reconhecimento de fala, processamento de linguagem natural, carros autônomos, detecção de tumor cerebral, tradução de fala em tempo real, música composição, jogo automático e assim por diante.

O aprendizado profundo é o próximo grande salto após o aprendizado de máquina com uma implementação mais avançada. Atualmente, está caminhando para se tornar um padrão da indústria, trazendo uma forte promessa de ser um divisor de águas ao lidar com dados não estruturados brutos.

O aprendizado profundo é atualmente um dos melhores provedores de soluções para uma ampla gama de problemas do mundo real. Os desenvolvedores estão construindo programas de IA que, em vez de usar regras fornecidas anteriormente, aprendem com exemplos para resolver tarefas complicadas. Com o aprendizado profundo sendo usado por muitos cientistas de dados, as redes neurais mais profundas estão entregando resultados cada vez mais precisos.

A ideia é desenvolver redes neurais profundas, aumentando o número de camadas de treinamento para cada rede; máquina aprende mais sobre os dados até que seja o mais preciso possível. Os desenvolvedores podem usar técnicas de aprendizado profundo para implementar tarefas complexas de aprendizado de máquina e treinar redes de IA para ter altos níveis de reconhecimento perceptivo.

O aprendizado profundo encontra sua popularidade na visão computacional. Aqui, uma das tarefas realizadas é a classificação de imagens, em que as imagens de entrada são classificadas como gato, cachorro, etc. ou como uma classe ou rótulo que melhor descreve a imagem. Nós, como humanos, aprendemos como fazer essa tarefa muito cedo em nossas vidas e temos essas habilidades de reconhecer padrões rapidamente, generalizar a partir do conhecimento anterior e nos adaptar a diferentes ambientes de imagem.

Neste capítulo, relacionaremos o aprendizado profundo às diferentes bibliotecas e estruturas.

Aprendizagem profunda e Theano

Se quisermos começar a codificar uma rede neural profunda, é melhor ter uma ideia de como diferentes frameworks como Theano, TensorFlow, Keras, PyTorch etc. funcionam.

Theano é uma biblioteca python que fornece um conjunto de funções para a construção de redes profundas que treinam rapidamente em nossa máquina.

Theano foi desenvolvido na Universidade de Montreal, Canadá, sob a liderança de Yoshua Bengio, um pioneiro da rede profunda.

Theano nos permite definir e avaliar expressões matemáticas com vetores e matrizes que são matrizes retangulares de números.

Tecnicamente falando, tanto as redes neurais quanto os dados de entrada podem ser representados como matrizes e todas as operações de rede padrão podem ser redefinidas como operações de matriz. Isso é importante porque os computadores podem realizar operações matriciais muito rapidamente.

Podemos processar vários valores de matriz em paralelo e, se construirmos uma rede neural com essa estrutura subjacente, podemos usar uma única máquina com uma GPU para treinar redes enormes em uma janela de tempo razoável.

No entanto, se usarmos Theano, temos que construir a rede profunda do zero. A biblioteca não fornece funcionalidade completa para a criação de um tipo específico de rede profunda.

Em vez disso, temos que codificar todos os aspectos da rede profunda, como o modelo, as camadas, a ativação, o método de treinamento e quaisquer métodos especiais para impedir o overfitting.

A boa notícia, entretanto, é que Theano permite a construção de nossa implementação sobre funções vetorizadas, fornecendo-nos uma solução altamente otimizada.

Existem muitas outras bibliotecas que estendem a funcionalidade do Theano. TensorFlow e Keras podem ser usados ​​com Theano como back-end.

Aprendizado profundo com TensorFlow

Googles TensorFlow é uma biblioteca python. Esta biblioteca é uma ótima opção para criar aplicativos de aprendizado profundo de nível comercial.

O TensorFlow cresceu a partir de outra biblioteca DistBelief V2 que fazia parte do Google Brain Project. Esta biblioteca visa estender a portabilidade do aprendizado de máquina para que os modelos de pesquisa possam ser aplicados a aplicativos de nível comercial.

Assim como a biblioteca Theano, o TensorFlow é baseado em gráficos computacionais em que um nó representa dados persistentes ou operações matemáticas e as bordas representam o fluxo de dados entre os nós, que é uma matriz multidimensional ou tensor; daí o nome TensorFlow

A saída de uma operação ou conjunto de operações é alimentada como entrada para a próxima.

Embora o TensorFlow tenha sido projetado para redes neurais, ele funciona bem para outras redes onde a computação pode ser modelada como gráfico de fluxo de dados.

O TensorFlow também usa vários recursos do Theano, como eliminação comum e de subexpressão, diferenciação automática, variáveis ​​compartilhadas e simbólicas.

Diferentes tipos de redes profundas podem ser construídas usando TensorFlow, como redes convolucionais, Autoencoders, RNTN, RNN, RBM, DBM / MLP e assim por diante.

No entanto, não há suporte para configuração de hiperparâmetro no TensorFlow. Para essa funcionalidade, podemos usar Keras.

Aprendizagem profunda e Keras

Keras é uma biblioteca Python poderosa e fácil de usar para desenvolver e avaliar modelos de aprendizado profundo.

Possui um design minimalista que nos permite construir uma rede camada por camada; treine-o e execute-o.

Ele envolve as bibliotecas de computação numérica eficientes Theano e TensorFlow e nos permite definir e treinar modelos de rede neural em algumas linhas curtas de código.

É uma API de rede neural de alto nível, ajudando a fazer amplo uso de aprendizado profundo e inteligência artificial. Ele é executado em várias bibliotecas de nível inferior, incluindo TensorFlow, Theano e assim por diante. O código Keras é portátil; podemos implementar uma rede neural em Keras usando Theano ou TensorFlow como back-end sem nenhuma alteração no código.

Nesta implementação de Deep learning, nosso objetivo é prever o atrito de clientes ou a rotatividade de dados para um determinado banco - quais clientes provavelmente deixarão este serviço bancário. O conjunto de dados usado é relativamente pequeno e contém 10.000 linhas com 14 colunas. Estamos usando a distribuição Anaconda e estruturas como Theano, TensorFlow e Keras. Keras é construído sobre Tensorflow e Theano, que funcionam como back-ends.

# Artificial Neural Network
# Installing Theano
pip install --upgrade theano

# Installing Tensorflow
pip install –upgrade tensorflow

# Installing Keras
pip install --upgrade keras

Etapa 1: pré-processamento de dados

In[]:

# Importing the libraries
   import numpy as np
   import matplotlib.pyplot as plt
   import pandas as pd
 
# Importing the database
   dataset = pd.read_csv('Churn_Modelling.csv')

Passo 2

Criamos matrizes das características do conjunto de dados e da variável de destino, que é a coluna 14, rotulada como “Exited”.

A aparência inicial dos dados é mostrada abaixo -

In[]:
X = dataset.iloc[:, 3:13].values
Y = dataset.iloc[:, 13].values
X

Resultado

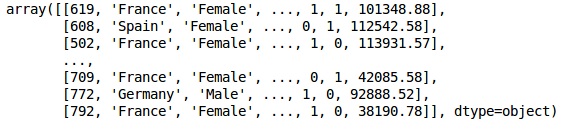
etapa 3

Y

Resultado

array([1, 0, 1, ..., 1, 1, 0], dtype = int64)

Passo 4

Tornamos a análise mais simples codificando variáveis ​​de string. Estamos usando a função ScikitLearn 'LabelEncoder' para codificar automaticamente os diferentes rótulos nas colunas com valores entre 0 e n_classes-1.

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder() 
X[:,1] = labelencoder_X_1.fit_transform(X[:,1]) 
labelencoder_X_2 = LabelEncoder() 
X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2])
X

Resultado

Na saída acima, os nomes dos países são substituídos por 0, 1 e 2; enquanto masculino e feminino são substituídos por 0 e 1.

Etapa 5

Labelling Encoded Data

Usamos o mesmo ScikitLearn biblioteca e outra função chamada de OneHotEncoder para apenas passar o número da coluna criando uma variável fictícia.

onehotencoder = OneHotEncoder(categorical features = [1])
X = onehotencoder.fit_transform(X).toarray()
X = X[:, 1:]
X

Agora, as 2 primeiras colunas representam o país e a 4ª coluna representa o gênero.

Resultado

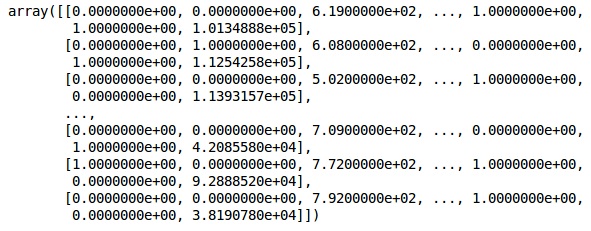
Sempre dividimos nossos dados em treinamento e parte de teste; treinamos nosso modelo em dados de treinamento e depois verificamos a precisão de um modelo em dados de teste, o que ajuda a avaliar a eficiência do modelo.

Etapa 6

Estamos usando o ScikitLearn's train_test_splitfunção para dividir nossos dados em conjunto de treinamento e conjunto de teste. Mantemos a taxa de divisão do trem para o teste em 80:20.

#Splitting the dataset into the Training set and the Test Set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

Algumas variáveis ​​têm valores em milhares, enquanto outras têm valores em dezenas ou unidades. Escalamos os dados para que sejam mais representativos.

Etapa 7

Neste código, estamos ajustando e transformando os dados de treinamento usando o StandardScalerfunção. Padronizamos nosso dimensionamento para que usemos o mesmo método ajustado para transformar / dimensionar os dados de teste.

# Feature Scaling

fromsklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)

Resultado

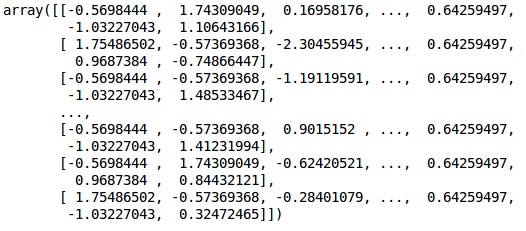
Os dados agora estão dimensionados corretamente. Finalmente, concluímos o nosso pré-processamento de dados. Agora, vamos começar com nosso modelo.

Etapa 8

Importamos os módulos necessários aqui. Precisamos do módulo Sequential para inicializar a rede neural e do módulo denso para adicionar as camadas ocultas.

# Importing the Keras libraries and packages 
import keras 
from keras.models import Sequential 
from keras.layers import Dense

Etapa 9

Chamaremos o modelo de Classificador, pois nosso objetivo é classificar a rotatividade de clientes. Em seguida, usamos o módulo Sequential para inicialização.

#Initializing Neural Network 
classifier = Sequential()

Etapa 10

Adicionamos as camadas ocultas uma a uma usando a função densa. No código abaixo, veremos muitos argumentos.

Nosso primeiro parâmetro é output_dim. É o número de nós que adicionamos a esta camada.inité a inicialização do Stochastic Gradient Decent. Em uma rede neural, atribuímos pesos a cada nó. Na inicialização, os pesos devem estar próximos de zero e nós inicializamos os pesos aleatoriamente usando a função uniforme. oinput_dimparâmetro é necessário apenas para a primeira camada, pois o modelo não conhece o número de nossas variáveis ​​de entrada. Aqui, o número total de variáveis ​​de entrada é 11. Na segunda camada, o modelo conhece automaticamente o número de variáveis ​​de entrada da primeira camada oculta.

Execute a seguinte linha de código para adicionar a camada de entrada e a primeira camada oculta -

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu', input_dim = 11))

Execute a seguinte linha de código para adicionar a segunda camada oculta -

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu'))

Execute a seguinte linha de código para adicionar a camada de saída -

classifier.add(Dense(units = 1, kernel_initializer = 'uniform', 
activation = 'sigmoid'))

Etapa 11

Compiling the ANN

Nós adicionamos várias camadas ao nosso classificador até agora. Agora iremos compilá-los usando ocompilemétodo. Os argumentos adicionados no controle de compilação final completam a rede neural. Portanto, precisamos ter cuidado nesta etapa.

Aqui está uma breve explicação dos argumentos.

O primeiro argumento é Optimizer.Este é um algoritmo usado para encontrar o conjunto ideal de pesos. Este algoritmo é chamado deStochastic Gradient Descent (SGD). Aqui, estamos usando um entre vários tipos, chamado de 'otimizador Adam'. O SGD depende da perda, então nosso segundo parâmetro é perda. Se nossa variável dependente for binária, usamos a função de perda logarítmica chamada‘binary_crossentropy’, e se nossa variável dependente tiver mais de duas categorias na saída, então usamos ‘categorical_crossentropy’. Queremos melhorar o desempenho de nossa rede neural com base emaccuracy, então adicionamos metrics como precisão.

# Compiling Neural Network 
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

Etapa 12

Vários códigos precisam ser executados nesta etapa.

Ajustando a ANN ao Conjunto de Treinamento

Agora treinamos nosso modelo nos dados de treinamento. Nós usamos ofitmétodo para se ajustar ao nosso modelo. Também otimizamos os pesos para melhorar a eficiência do modelo. Para isso, temos que atualizar os pesos.Batch size é o número de observações após as quais atualizamos os pesos. Epoché o número total de iterações. Os valores de tamanho do lote e época são escolhidos pelo método de tentativa e erro.

classifier.fit(X_train, y_train, batch_size = 10, epochs = 50)

Fazendo previsões e avaliando o modelo

# Predicting the Test set results
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)

Prevendo uma única nova observação

# Predicting a single new observation
"""Our goal is to predict if the customer with the following data will leave the bank:
Geography: Spain
Credit Score: 500
Gender: Female
Age: 40
Tenure: 3
Balance: 50000
Number of Products: 2
Has Credit Card: Yes
Is Active Member: Yes

Etapa 13

Predicting the test set result

O resultado da previsão lhe dará a probabilidade de o cliente sair da empresa. Vamos converter essa probabilidade em 0 e 1 binários.

# Predicting the Test set results 
y_pred = classifier.predict(X_test) 
y_pred = (y_pred > 0.5)

new_prediction = classifier.predict(sc.transform
(np.array([[0.0, 0, 500, 1, 40, 3, 50000, 2, 1, 1, 40000]])))
new_prediction = (new_prediction > 0.5)

Etapa 14

Esta é a última etapa em que avaliamos o desempenho do nosso modelo. Já temos resultados originais e, portanto, podemos construir uma matriz de confusão para verificar a precisão do nosso modelo.

Making the Confusion Matrix

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print (cm)

Resultado

loss: 0.3384 acc: 0.8605
[ [1541 54]
[230 175] ]

A partir da matriz de confusão, a precisão do nosso modelo pode ser calculada como -

Accuracy = 1541+175/2000=0.858

We achieved 85.8% accuracy, qual é bom.

O Algoritmo de Propagação Direta

Nesta seção, aprenderemos como escrever código para fazer propagação direta (predição) para uma rede neural simples -

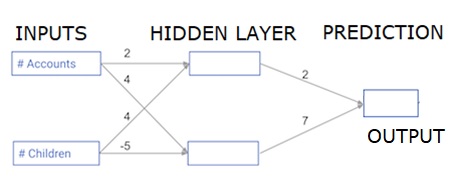
Cada ponto de dados é um cliente. A primeira entrada é quantas contas eles têm, e a segunda entrada é quantos filhos eles têm. O modelo irá prever quantas transações o usuário fará no próximo ano.

Os dados de entrada são pré-carregados como dados de entrada e os pesos estão em um dicionário chamado pesos. A matriz de pesos para o primeiro nó na camada oculta está em pesos ['nó_0'], e para o segundo nó na camada oculta estão em pesos ['nó_1'] respectivamente.

Os pesos que alimentam o nó de saída estão disponíveis em pesos.

A função de ativação linear retificada

Uma "função de ativação" é uma função que funciona em cada nó. Ele transforma a entrada do nó em alguma saída.

A função de ativação linear retificada (chamada ReLU ) é amplamente utilizada em redes de alto desempenho. Esta função recebe um único número como entrada, retornando 0 se a entrada for negativa e como saída se a entrada for positiva.

Aqui estão alguns exemplos -

• relu (4) = 4
• relu (-2) = 0

Preenchemos a definição da função relu () -

• Usamos a função max () para calcular o valor da saída de relu ().
• Aplicamos a função relu () a node_0_input para calcular node_0_output.
• Aplicamos a função relu () a node_1_input para calcular node_1_output.

import numpy as np
input_data = np.array([-1, 2])
weights = {
   'node_0': np.array([3, 3]),
   'node_1': np.array([1, 5]),
   'output': np.array([2, -1])
}
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = np.tanh(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = np.tanh(node_1_input)
hidden_layer_output = np.array(node_0_output, node_1_output)
output =(hidden_layer_output * weights['output']).sum()
print(output)

def relu(input):
   '''Define your relu activation function here'''
   # Calculate the value for the output of the relu function: output
   output = max(input,0)
      # Return the value just calculated
   return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)

# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)

# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])

# Calculate model output (do not apply relu)
odel_output = (hidden_layer_outputs * weights['output']).sum()
print(model_output)# Print model output

Resultado

0.9950547536867305
-3

Aplicando a rede a muitas observações / linhas de dados

Nesta seção, aprenderemos como definir uma função chamada predict_with_network (). Esta função irá gerar previsões para múltiplas observações de dados, tomadas da rede acima, tomadas como dados_de_entrada. Os pesos dados na rede acima estão sendo usados. A definição da função relu () também está sendo usada.

Vamos definir uma função chamada predict_with_network () que aceita dois argumentos - input_data_row e pesos - e retorna uma previsão da rede como saída.

Calculamos os valores de entrada e saída para cada nó, armazenando-os como: node_0_input, node_0_output, node_1_input e node_1_output.

Para calcular o valor de entrada de um nó, multiplicamos as matrizes relevantes e calculamos sua soma.

Para calcular o valor de saída de um nó, aplicamos a função relu () ao valor de entrada do nó. Usamos um 'for loop' para iterar sobre input_data -

Também usamos nosso predict_with_network () para gerar previsões para cada linha do input_data - input_data_row. Também anexamos cada previsão aos resultados.

# Define predict_with_network()
def predict_with_network(input_data_row, weights):
   # Calculate node 0 value
   node_0_input = (input_data_row * weights['node_0']).sum()
   node_0_output = relu(node_0_input)
   
   # Calculate node 1 value
   node_1_input = (input_data_row * weights['node_1']).sum()
   node_1_output = relu(node_1_input)
   
   # Put node values into array: hidden_layer_outputs
   hidden_layer_outputs = np.array([node_0_output, node_1_output])
   
   # Calculate model output
   input_to_final_layer = (hidden_layer_outputs*weights['output']).sum()
   model_output = relu(input_to_final_layer)
# Return model output
   return(model_output)

# Create empty list to store prediction results
results = []
for input_data_row in input_data:
   # Append prediction to results
   results.append(predict_with_network(input_data_row, weights))
print(results)# Print results

Resultado

[0, 12]

Aqui, usamos a função relu onde relu (26) = 26 e relu (-13) = 0 e assim por diante.

Redes neurais multi-camadas profundas

Aqui, estamos escrevendo um código para fazer a propagação direta para uma rede neural com duas camadas ocultas. Cada camada oculta possui dois nós. Os dados de entrada foram pré-carregados comoinput_data. Os nós na primeira camada oculta são chamados de node_0_0 e node_0_1.

Seus pesos são pré-carregados como pesos ['node_0_0'] e pesos ['node_0_1'] respectivamente.

Os nós na segunda camada oculta são chamados node_1_0 and node_1_1. Seus pesos são pré-carregados comoweights['node_1_0'] e weights['node_1_1'] respectivamente.

Em seguida, criamos uma saída de modelo a partir dos nós ocultos usando pesos pré-carregados como weights['output'].

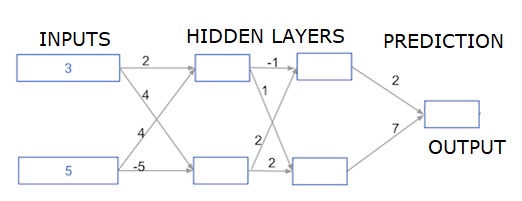
Calculamos node_0_0_input usando seus pesos, pesos ['node_0_0'] e os dados de entrada fornecidos. Em seguida, aplique a função relu () para obter node_0_0_output.

Fazemos o mesmo que acima para node_0_1_input para obter node_0_1_output.

Calculamos node_1_0_input usando seus pesos, pesos ['node_1_0'] e as saídas da primeira camada oculta - hidden_0_outputs. Em seguida, aplicamos a função relu () para obter node_1_0_output.

Fazemos o mesmo que acima para node_1_1_input para obter node_1_1_output.

Calculamos model_output usando pesos ['output'] e os outputs da segunda camada escondida, hidden_1_outputs array. Não aplicamos a função relu () a esta saída.

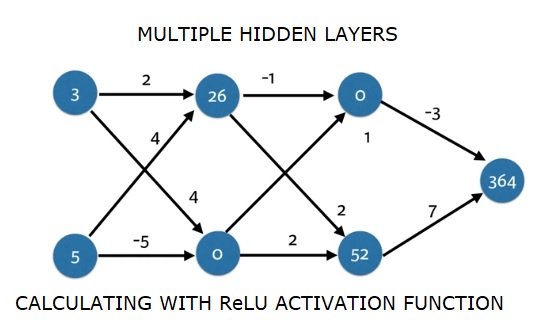
import numpy as np
input_data = np.array([3, 5])
weights = {
   'node_0_0': np.array([2, 4]),
   'node_0_1': np.array([4, -5]),
   'node_1_0': np.array([-1, 1]),
   'node_1_1': np.array([2, 2]),
   'output': np.array([2, 7])
}
def predict_with_network(input_data):
   # Calculate node 0 in the first hidden layer
   node_0_0_input = (input_data * weights['node_0_0']).sum()
   node_0_0_output = relu(node_0_0_input)
   
   # Calculate node 1 in the first hidden layer
   node_0_1_input = (input_data*weights['node_0_1']).sum()
   node_0_1_output = relu(node_0_1_input)
   
   # Put node values into array: hidden_0_outputs
   hidden_0_outputs = np.array([node_0_0_output, node_0_1_output])
   
   # Calculate node 0 in the second hidden layer
   node_1_0_input = (hidden_0_outputs*weights['node_1_0']).sum()
   node_1_0_output = relu(node_1_0_input)
   
   # Calculate node 1 in the second hidden layer
   node_1_1_input = (hidden_0_outputs*weights['node_1_1']).sum()
   node_1_1_output = relu(node_1_1_input)
   
   # Put node values into array: hidden_1_outputs
   hidden_1_outputs = np.array([node_1_0_output, node_1_1_output])
   
   # Calculate model output: model_output
   model_output = (hidden_1_outputs*weights['output']).sum()
      # Return model_output
   return(model_output)
output = predict_with_network(input_data)
print(output)

Resultado

364