PyTorch - Regressão Linear

Neste capítulo, vamos nos concentrar no exemplo básico de implementação de regressão linear usando o TensorFlow. A regressão logística ou regressão linear é uma abordagem de aprendizado de máquina supervisionada para a classificação de categorias discretas de ordem. Nosso objetivo neste capítulo é construir um modelo pelo qual um usuário pode prever o relacionamento entre variáveis ​​preditoras e uma ou mais variáveis ​​independentes.

A relação entre essas duas variáveis ​​é considerada linear, ou seja, se y é a variável dependente ex é considerada a variável independente, então a relação de regressão linear de duas variáveis ​​será semelhante à equação mencionada abaixo -

Y = Ax+b

Em seguida, devemos projetar um algoritmo para regressão linear que nos permite entender dois conceitos importantes dados abaixo -

• Função de Custo
• Algoritmos de gradiente descendente

A representação esquemática da regressão linear é mencionada abaixo

Interpretando o resultado

$$ Y = ax + b $$

• O valor de a é a inclinação.

• O valor de b é o y − intercept.

• r é o correlation coefficient.

• r² é o correlation coefficient.

A visão gráfica da equação de regressão linear é mencionada abaixo -

As etapas a seguir são usadas para implementar a regressão linear usando PyTorch -

Passo 1

Importe os pacotes necessários para criar uma regressão linear em PyTorch usando o código abaixo -

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline

sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = True

Passo 2

Crie um único conjunto de treinamento com o conjunto de dados disponível conforme mostrado abaixo -

m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)

noise = np.random.randn(256) / 4

y = x * m + c + noise

df = pd.DataFrame()
df['x'] = x
df['y'] = y

sns.lmplot(x ='x', y ='y', data = df)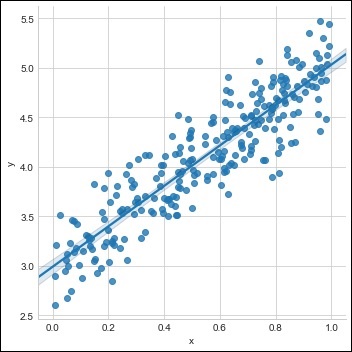

etapa 3

Implementar regressão linear com bibliotecas PyTorch conforme mencionado abaixo -

import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

class LinearRegressionModel(nn.Module):
   def __init__(self, input_dim, output_dim):
      super(LinearRegressionModel, self).__init__()
      self.linear = nn.Linear(input_dim, output_dim)

   def forward(self, x):
      out = self.linear(x)
      return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()

def get_param_values():
   return w.data[0][0], b.data[0]

def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')

O gráfico gerado é o seguinte -