Comunicação por satélite - Leis de Kepler
Sabemos que o satélite gira em torno da Terra, que é semelhante ao que a Terra gira em torno do sol. Portanto, os princípios que são aplicados à Terra e seu movimento ao redor do Sol também são aplicáveis ao satélite e seu movimento ao redor da Terra.
Muitos cientistas apresentaram diferentes tipos de teorias desde os primeiros tempos. Se apenasJohannes Kepler (1571-1630) foi um dos cientistas mais aceitos na descrição do princípio de um satélite que se move ao redor da Terra.
Kepler formulou três leis que mudaram toda a teoria e observações da comunicação por satélite. Estes são conhecidos popularmente comoKepler’s laws. Eles são úteis para visualizar o movimento através do espaço.
Primeira Lei de Kepler
A primeira lei de Kepler afirma que o caminho seguido por um satélite em torno de seu principal (a Terra) será um ellipse. Esta elipse possui dois pontos focais (focos) F1 e F2 conforme mostrado na figura abaixo. O centro de massa da Terra sempre estará presente em um dos dois focos da elipse.
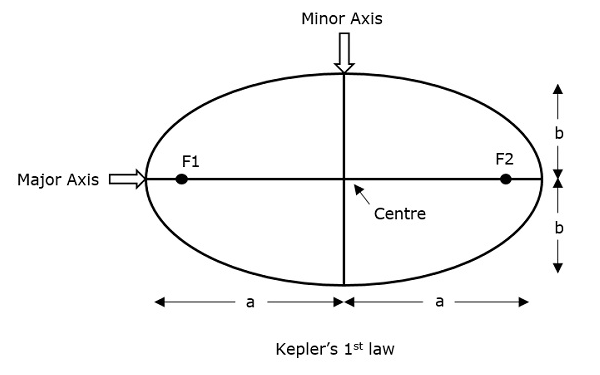
Se a distância do centro do objeto a um ponto em seu caminho elíptico for considerada, o ponto mais distante de uma elipse do centro é chamado de apogee e o ponto mais curto de uma elipse do centro é chamado de perigee.
Eccentricity "e" deste sistema pode ser escrito como -
$$ e = \ frac {\ sqrt {a ^ 2 - b ^ 2}} {a} $$
Onde, a E b são os comprimentos do semi-eixo maior e do semi-eixo menor da elipse, respectivamente.
Para um elliptical path, o valor da excentricidade (e) está sempre entre 0 e 1, ou seja, $ 0 $ < $ e $ < $ 1 $ , já que a é maior que b. Suponha que, se o valor da excentricidade (e) for zero, o caminho não terá mais forma elíptica, mas será convertido em uma forma circular.
Segunda Lei de Kepler
A segunda lei de Kepler afirma que, para intervalos iguais de tempo, o areacoberto pelo satélite será o mesmo em relação ao centro de massa da Terra. Isso pode ser entendido observando a figura a seguir.
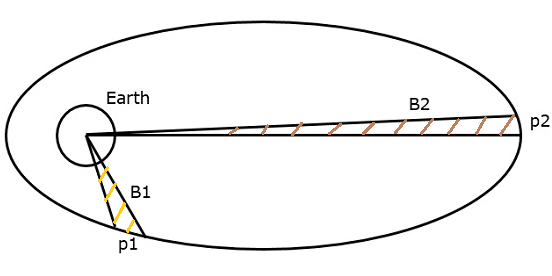
Suponha que o satélite cubra as distâncias p1 e p2 no mesmo intervalo de tempo. Então, as áreas B1 e B2 cobertas pelo satélite nessas duas instâncias são iguais.
Terceira Lei de Kepler
A terceira lei de Kepler afirma que o quadrado do tempo periódico de uma órbita elíptica é proporcional ao cubo do comprimento do semieixo maior. Mathematically, pode ser escrito da seguinte forma -
$$ T ^ 2 \: \ alpha \: a ^ 3 $$
$$ => T ^ 2 = \ left (\ frac {4 \ pi ^ 2} {\ mu} \ right) a ^ 3 $$
Onde, $ \ frac {4 \ pi ^ 2} {\ mu} $ é a constante de proporcionalidade.
$ \ mu $ é a constante de Kepler e seu valor é igual a 3,986005 x 10 14 m 3 / s 2
$$ 1 = \ left (\ frac {2 \ pi} {T} \ right) ^ 2 \ left (\ frac {a ^ 2} {\ mu} \ right) $$
$$ 1 = n ^ 2 \ left (\ frac {a ^ 3} {\ mu} \ right) $$
$$ => a ^ 3 = \ frac {\ mu} {n ^ 2} $$
Onde, ‘n’ é o movimento médio do satélite em radianos por segundo.
Note- Um satélite, quando gira em torno da Terra, sofre uma força de tração da Terra, que é a força gravitacional. Da mesma forma, ele experimenta outra força de atração do sol e da lua. Portanto, um satélite deve equilibrar essas duas forças para se manter em sua órbita.