Scikit Learn - Guia rápido
Neste capítulo, entenderemos o que é Scikit-Learn ou Sklearn, origem do Scikit-Learn e alguns outros tópicos relacionados, como comunidades e colaboradores responsáveis pelo desenvolvimento e manutenção do Scikit-Learn, seus pré-requisitos, instalação e seus recursos.
O que é Scikit-Learn (Sklearn)
Scikit-learn (Sklearn) é a biblioteca mais útil e robusta para aprendizado de máquina em Python. Ele fornece uma seleção de ferramentas eficientes para aprendizado de máquina e modelagem estatística, incluindo classificação, regressão, agrupamento e redução de dimensionalidade por meio de uma interface de consistência em Python. Esta biblioteca, que é amplamente escrita em Python, é construída sobreNumPy, SciPy e Matplotlib.
Origem do Scikit-Learn
Foi originalmente chamado scikits.learn e foi inicialmente desenvolvido por David Cournapeau como um projeto de verão do código do Google em 2007. Mais tarde, em 2010, Fabian Pedregosa, Gael Varoquaux, Alexandre Gramfort e Vincent Michel, do FIRCA (Instituto Francês de Pesquisa em Ciência da Computação e Automação), tomaram este projeto em outro nível e fez o primeiro lançamento público (v0.1 beta) em 1º de fevereiro de 2010.
Vamos dar uma olhada em seu histórico de versões -
Maio de 2019: scikit-learn 0.21.0
Março de 2019: scikit-learn 0.20.3
Dezembro de 2018: scikit-learn 0.20.2
Novembro de 2018: scikit-learn 0.20.1
Setembro de 2018: scikit-learn 0.20.0
Julho de 2018: scikit-learn 0.19.2
Julho de 2017: scikit-learn 0.19.0
Setembro de 2016. scikit-learn 0.18.0
Novembro de 2015. scikit-learn 0.17.0
Março de 2015. scikit-learn 0.16.0
Julho de 2014. scikit-learn 0.15.0
Agosto de 2013. scikit-learn 0.14
Comunidade e colaboradores
O Scikit-learn é um esforço da comunidade e qualquer pessoa pode contribuir para isso. Este projeto está hospedado emhttps://github.com/scikit-learn/scikit-learn. As pessoas a seguir são atualmente os principais contribuintes para o desenvolvimento e manutenção do Sklearn -
Joris Van den Bossche (cientista de dados)
Thomas J Fan (desenvolvedor de software)
Alexandre Gramfort (pesquisador de aprendizado de máquina)
Olivier Grisel (especialista em aprendizado de máquina)
Nicolas Hug (cientista pesquisador associado)
Andreas Mueller (cientista em aprendizado de máquina)
Hanmin Qin (engenheiro de software)
Adrin Jalali (desenvolvedor de código aberto)
Nelle Varoquaux (pesquisadora de ciência de dados)
Roman Yurchak (cientista de dados)
Várias organizações como Booking.com, JP Morgan, Evernote, Inria, AWeber, Spotify e muitas outras estão usando o Sklearn.
Pré-requisitos
Antes de começarmos a usar a última versão do scikit-learn, exigimos o seguinte -
Python (> = 3,5)
NumPy (> = 1.11.0)
Scipy (> = 0,17,0) li
Joblib (> = 0,11)
Matplotlib (> = 1.5.1) é necessário para recursos de plotagem do Sklearn.
Pandas (> = 0.18.0) é necessário para alguns dos exemplos do scikit-learn usando estrutura e análise de dados.
Instalação
Se você já instalou o NumPy e o Scipy, a seguir estão as duas maneiras mais fáceis de instalar o scikit-learn -
Usando pip
O seguinte comando pode ser usado para instalar o scikit-learn via pip -
pip install -U scikit-learnUsando conda
O seguinte comando pode ser usado para instalar o scikit-learn via conda -
conda install scikit-learnPor outro lado, se o NumPy e o Scipy ainda não estiverem instalados em sua estação de trabalho Python, você pode instalá-los usando qualquer pip ou conda.
Outra opção para usar o scikit-learn é usar distribuições Python como Canopy e Anaconda porque ambos fornecem a versão mais recente do scikit-learn.
Características
Em vez de focar em carregar, manipular e resumir dados, a biblioteca Scikit-learn está focada em modelar os dados. Alguns dos grupos de modelos mais populares fornecidos pela Sklearn são os seguintes -
Supervised Learning algorithms - Quase todos os algoritmos de aprendizagem supervisionada populares, como regressão linear, máquina de vetores de suporte (SVM), árvore de decisão, etc., fazem parte do scikit-learn.
Unsupervised Learning algorithms - Por outro lado, ele também tem todos os algoritmos populares de aprendizagem não supervisionada de clustering, análise de fator, PCA (Análise de Componentes Principais) para redes neurais não supervisionadas.
Clustering - Este modelo é usado para agrupar dados não rotulados.
Cross Validation - É usado para verificar a precisão dos modelos supervisionados em dados não vistos.
Dimensionality Reduction - É usado para reduzir o número de atributos em dados que podem ser usados posteriormente para resumo, visualização e seleção de recursos.
Ensemble methods - Como o nome sugere, é usado para combinar as previsões de vários modelos supervisionados.
Feature extraction - É usado para extrair os recursos dos dados para definir os atributos nos dados de imagem e texto.
Feature selection - É usado para identificar atributos úteis para criar modelos supervisionados.
Open Source - É uma biblioteca de código aberto e também utilizável comercialmente sob a licença BSD.
Este capítulo trata do processo de modelagem envolvido no Sklearn. Vamos entender sobre o mesmo em detalhes e começar com o carregamento do conjunto de dados.
Carregando o conjunto de dados
Uma coleção de dados é chamada de conjunto de dados. Ele tem os dois componentes a seguir -
Features- As variáveis de dados são chamadas de seus recursos. Eles também são conhecidos como preditores, entradas ou atributos.
Feature matrix - É a coleção de recursos, caso haja mais de um.
Feature Names - É a lista de todos os nomes dos recursos.
Response- É a variável de saída que depende basicamente das variáveis de recursos. Eles também são conhecidos como destino, rótulo ou saída.
Response Vector- É usado para representar a coluna de resposta. Geralmente, temos apenas uma coluna de resposta.
Target Names - Representa os valores possíveis assumidos por um vetor de resposta.
Scikit-learn tem alguns exemplos de conjuntos de dados como iris e digits para classificação e o Boston house prices para regressão.
Exemplo
A seguir está um exemplo para carregar iris conjunto de dados -
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
print("Feature names:", feature_names)
print("Target names:", target_names)
print("\nFirst 10 rows of X:\n", X[:10])Resultado
Feature names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Target names: ['setosa' 'versicolor' 'virginica']
First 10 rows of X:
[
[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
[5.4 3.9 1.7 0.4]
[4.6 3.4 1.4 0.3]
[5. 3.4 1.5 0.2]
[4.4 2.9 1.4 0.2]
[4.9 3.1 1.5 0.1]
]Dividindo o conjunto de dados
Para verificar a precisão do nosso modelo, podemos dividir o conjunto de dados em duas partes-a training set e a testing set. Use o conjunto de treinamento para treinar o modelo e o conjunto de teste para testar o modelo. Depois disso, podemos avaliar o desempenho do nosso modelo.
Exemplo
O exemplo a seguir dividirá os dados na proporção de 70:30, ou seja, 70% dos dados serão usados como dados de treinamento e 30% como dados de teste. O conjunto de dados é um conjunto de dados da íris como no exemplo acima.
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.3, random_state = 1
)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)Resultado
(105, 4)
(45, 4)
(105,)
(45,)Como visto no exemplo acima, ele usa train_test_split()função do scikit-learn para dividir o conjunto de dados. Esta função possui os seguintes argumentos -
X, y - Aqui, X é o feature matrix e y é o response vector, que precisa ser dividido.
test_size- Isso representa a proporção dos dados de teste em relação ao total de dados fornecidos. Como no exemplo acima, estamos definindotest_data = 0.3 para 150 linhas de X. Isso produzirá dados de teste de 150 * 0,3 = 45 linhas.
random_size- É utilizado para garantir que a divisão será sempre a mesma. Isso é útil nas situações em que você deseja resultados reproduzíveis.
Treine o modelo
Em seguida, podemos usar nosso conjunto de dados para treinar algum modelo de previsão. Conforme discutido, o scikit-learn tem uma ampla gama deMachine Learning (ML) algorithms que têm uma interface consistente para ajuste, previsão de precisão, recall etc.
Exemplo
No exemplo abaixo, vamos usar o classificador KNN (K vizinhos mais próximos). Não entre em detalhes sobre algoritmos KNN, pois haverá um capítulo separado para isso. Este exemplo é usado para fazer você entender apenas a parte de implementação.
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.4, random_state=1
)
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
classifier_knn = KNeighborsClassifier(n_neighbors = 3)
classifier_knn.fit(X_train, y_train)
y_pred = classifier_knn.predict(X_test)
# Finding accuracy by comparing actual response values(y_test)with predicted response value(y_pred)
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
# Providing sample data and the model will make prediction out of that data
sample = [[5, 5, 3, 2], [2, 4, 3, 5]]
preds = classifier_knn.predict(sample)
pred_species = [iris.target_names[p] for p in preds] print("Predictions:", pred_species)Resultado
Accuracy: 0.9833333333333333
Predictions: ['versicolor', 'virginica']Persistência do modelo
Depois de treinar o modelo, é desejável que ele seja persistente para uso futuro, para que não precisemos treiná-lo novamente e novamente. Isso pode ser feito com a ajuda dedump e load características de joblib pacote.
Considere o exemplo abaixo, no qual salvaremos o modelo treinado acima (classifier_knn) para uso futuro -
from sklearn.externals import joblib
joblib.dump(classifier_knn, 'iris_classifier_knn.joblib')O código acima salvará o modelo em um arquivo denominado iris_classifier_knn.joblib. Agora, o objeto pode ser recarregado do arquivo com a ajuda do seguinte código -
joblib.load('iris_classifier_knn.joblib')Pré-processamento dos dados
Como estamos lidando com muitos dados e esses dados estão na forma bruta, antes de inserir esses dados em algoritmos de aprendizado de máquina, precisamos convertê-los em dados significativos. Esse processo é chamado de pré-processamento dos dados. Scikit-learn tem um pacote chamadopreprocessingpara este propósito. opreprocessing pacote tem as seguintes técnicas -
Binarização
Essa técnica de pré-processamento é usada quando precisamos converter nossos valores numéricos em valores booleanos.
Exemplo
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]]
)
data_binarized = preprocessing.Binarizer(threshold=0.5).transform(input_data)
print("\nBinarized data:\n", data_binarized)No exemplo acima, usamos threshold value = 0,5 e é por isso que todos os valores acima de 0,5 seriam convertidos em 1 e todos os valores abaixo de 0,5 seriam convertidos em 0.
Resultado
Binarized data:
[
[ 1. 0. 1.]
[ 0. 1. 1.]
[ 0. 0. 1.]
[ 1. 1. 0.]
]Remoção Média
Esta técnica é usada para eliminar a média do vetor de recurso de forma que cada recurso seja centralizado em zero.
Exemplo
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]]
)
#displaying the mean and the standard deviation of the input data
print("Mean =", input_data.mean(axis=0))
print("Stddeviation = ", input_data.std(axis=0))
#Removing the mean and the standard deviation of the input data
data_scaled = preprocessing.scale(input_data)
print("Mean_removed =", data_scaled.mean(axis=0))
print("Stddeviation_removed =", data_scaled.std(axis=0))Resultado
Mean = [ 1.75 -1.275 2.2 ]
Stddeviation = [ 2.71431391 4.20022321 4.69414529]
Mean_removed = [ 1.11022302e-16 0.00000000e+00 0.00000000e+00]
Stddeviation_removed = [ 1. 1. 1.]Dimensionamento
Usamos essa técnica de pré-processamento para dimensionar os vetores de recursos. O dimensionamento dos vetores de recursos é importante, porque os recursos não devem ser sinteticamente grandes ou pequenos.
Exemplo
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_scaler_minmax = preprocessing.MinMaxScaler(feature_range=(0,1))
data_scaled_minmax = data_scaler_minmax.fit_transform(input_data)
print ("\nMin max scaled data:\n", data_scaled_minmax)Resultado
Min max scaled data:
[
[ 0.48648649 0.58252427 0.99122807]
[ 0. 1. 0.81578947]
[ 0.27027027 0. 1. ]
[ 1. 0.99029126 0. ]
]Normalização
Usamos essa técnica de pré-processamento para modificar os vetores de recursos. A normalização dos vetores de recursos é necessária para que os vetores de recursos possam ser medidos em uma escala comum. Existem dois tipos de normalização, como segue -
Normalização L1
É também chamado de Desvios Mínimos Absolutos. Modifica o valor de forma que a soma dos valores absolutos permaneça sempre até 1 em cada linha. O exemplo a seguir mostra a implementação da normalização L1 nos dados de entrada.
Exemplo
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_normalized_l1 = preprocessing.normalize(input_data, norm='l1')
print("\nL1 normalized data:\n", data_normalized_l1)Resultado
L1 normalized data:
[
[ 0.22105263 -0.2 0.57894737]
[-0.2027027 0.32432432 0.47297297]
[ 0.03571429 -0.56428571 0.4 ]
[ 0.42142857 0.16428571 -0.41428571]
]Normalização L2
Também chamado de Least Squares. Ele modifica o valor de forma que a soma dos quadrados permaneça sempre até 1 em cada linha. O exemplo a seguir mostra a implementação da normalização L2 nos dados de entrada.
Exemplo
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_normalized_l2 = preprocessing.normalize(input_data, norm='l2')
print("\nL1 normalized data:\n", data_normalized_l2)Resultado
L2 normalized data:
[
[ 0.33946114 -0.30713151 0.88906489]
[-0.33325106 0.53320169 0.7775858 ]
[ 0.05156558 -0.81473612 0.57753446]
[ 0.68706914 0.26784051 -0.6754239 ]
]Como sabemos, o aprendizado de máquina está prestes a criar um modelo a partir de dados. Para isso, o computador deve primeiro entender os dados. A seguir, vamos discutir várias maneiras de representar os dados para serem entendidos pelo computador -
Dados como tabela
A melhor maneira de representar dados no Scikit-learn é na forma de tabelas. Uma tabela representa uma grade 2-D de dados em que as linhas representam os elementos individuais do conjunto de dados e as colunas representam as quantidades relacionadas a esses elementos individuais.
Exemplo
Com o exemplo dado abaixo, podemos baixar iris dataset na forma de um DataFrame Pandas com a ajuda de python seaborn biblioteca.
import seaborn as sns
iris = sns.load_dataset('iris')
iris.head()Resultado
sepal_length sepal_width petal_length petal_width species
0 5.1 3.5 1.4 0.2 setosa
1 4.9 3.0 1.4 0.2 setosa
2 4.7 3.2 1.3 0.2 setosa
3 4.6 3.1 1.5 0.2 setosa
4 5.0 3.6 1.4 0.2 setosaA partir da saída acima, podemos ver que cada linha dos dados representa uma única flor observada e o número de linhas representa o número total de flores no conjunto de dados. Geralmente, nos referimos às linhas da matriz como amostras.
Por outro lado, cada coluna de dados representa uma informação quantitativa que descreve cada amostra. Geralmente, nos referimos às colunas da matriz como recursos.
Dados como matriz de recursos
A matriz de recursos pode ser definida como o layout da tabela em que as informações podem ser consideradas como uma matriz 2-D. Ele é armazenado em uma variável chamadaXe assumido ser bidimensional com forma [n_samples, n_features]. Principalmente, ele está contido em uma matriz NumPy ou em um Pandas DataFrame. Como dito anteriormente, as amostras sempre representam os objetos individuais descritos pelo conjunto de dados e os recursos representam as observações distintas que descrevem cada amostra de maneira quantitativa.
Dados como matriz de destino
Junto com a matriz de recursos, denotada por X, também temos a matriz de destino. Também é chamado de rótulo. É denotado por y. O rótulo ou matriz de destino é geralmente unidimensional com comprimento n_samples. Geralmente está contido no NumPyarray ou pandas Series. A matriz de destino pode ter os valores, valores numéricos contínuos e valores discretos.
Como a matriz de destino difere das colunas de recursos?
Podemos distinguir ambos por um ponto que a matriz de destino geralmente é a quantidade que queremos prever a partir dos dados, ou seja, em termos estatísticos, é a variável dependente.
Exemplo
No exemplo abaixo, a partir do conjunto de dados da íris, prevemos as espécies de flores com base nas outras medições. Nesse caso, a coluna Espécie seria considerada como o recurso.
import seaborn as sns
iris = sns.load_dataset('iris')
%matplotlib inline
import seaborn as sns; sns.set()
sns.pairplot(iris, hue='species', height=3);Resultado
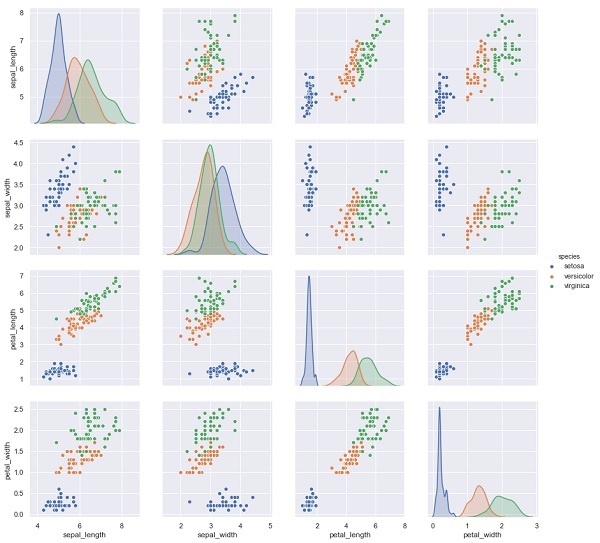
X_iris = iris.drop('species', axis=1)
X_iris.shape
y_iris = iris['species']
y_iris.shapeResultado
(150,4)
(150,)Neste capítulo, aprenderemos sobre Estimator API(interface de programação de aplicativo). Vamos começar entendendo o que é uma API Estimator.
O que é API Estimator
É uma das principais APIs implementadas pelo Scikit-learn. Ele fornece uma interface consistente para uma ampla gama de aplicativos de ML, por isso todos os algoritmos de aprendizado de máquina no Scikit-Learn são implementados por meio da API Estimator. O objeto que aprende com os dados (ajustando os dados) é um estimador. Pode ser usado com qualquer um dos algoritmos como classificação, regressão, clustering ou mesmo com um transformador, que extrai recursos úteis de dados brutos.
Para ajustar os dados, todos os objetos estimadores expõem um método de ajuste que leva um conjunto de dados mostrado a seguir -
estimator.fit(data)A seguir, todos os parâmetros de um estimador podem ser definidos, da seguinte maneira, quando ele é instanciado pelo atributo correspondente.
estimator = Estimator (param1=1, param2=2)
estimator.param1A saída do acima seria 1.
Uma vez que os dados são ajustados com um estimador, os parâmetros são estimados a partir dos dados disponíveis. Agora, todos os parâmetros estimados serão os atributos do objeto estimador terminando por um sublinhado da seguinte forma -
estimator.estimated_param_Uso da API Estimator
Os principais usos dos estimadores são os seguintes -
Estimativa e decodificação de um modelo
O objeto Estimador é usado para estimativa e decodificação de um modelo. Além disso, o modelo é estimado como uma função determinística do seguinte -
Os parâmetros fornecidos na construção do objeto.
O estado aleatório global (numpy.random) se o parâmetro random_state do estimador for definido como nenhum.
Quaisquer dados passados para a chamada mais recente para fit, fit_transform, or fit_predict.
Quaisquer dados passados em uma sequência de chamadas para partial_fit.
Mapeamento de representação de dados não retangulares em dados retangulares
Ele mapeia uma representação de dados não retangular em dados retangulares. Em palavras simples, é necessária uma entrada onde cada amostra não é representada como um objeto semelhante a uma matriz de comprimento fixo e produz um objeto semelhante a uma matriz de características para cada amostra.
Distinção entre amostras centrais e periféricas
Ele modela a distinção entre amostras centrais e periféricas usando os seguintes métodos -
fit
fit_predict se transdutivo
prever se indutivo
Princípios Orientadores
Ao projetar a API Scikit-Learn, seguindo os princípios orientadores mantidos em mente -
Consistência
Este princípio afirma que todos os objetos devem compartilhar uma interface comum desenhada a partir de um conjunto limitado de métodos. A documentação também deve ser consistente.
Hierarquia limitada de objetos
Este princípio orientador diz -
Algoritmos devem ser representados por classes Python
Os conjuntos de dados devem ser representados no formato padrão como matrizes NumPy, Pandas DataFrames, matriz esparsa SciPy.
Os nomes dos parâmetros devem usar strings Python padrão.
Composição
Como sabemos, os algoritmos de ML podem ser expressos como a sequência de muitos algoritmos fundamentais. O Scikit-learn usa esses algoritmos fundamentais sempre que necessário.
Padrões sensatos
De acordo com esse princípio, a biblioteca Scikit-learn define um valor padrão apropriado sempre que os modelos de ML exigem parâmetros especificados pelo usuário.
Inspeção
De acordo com este princípio orientador, cada valor de parâmetro especificado é exposto como atributos públicos.
Etapas no uso da API Estimator
A seguir estão as etapas de uso da API do estimador Scikit-Learn -
Etapa 1: Escolha uma classe de modelo
Nesta primeira etapa, precisamos escolher uma classe de modelo. Isso pode ser feito importando a classe Estimator apropriada do Scikit-learn.
Etapa 2: escolha os hiperparâmetros do modelo
Nesta etapa, precisamos escolher hiperparâmetros do modelo de classe. Isso pode ser feito instanciando a classe com os valores desejados.
Etapa 3: Organizando os dados
Em seguida, precisamos organizar os dados em matriz de características (X) e vetor de destino (y).
Etapa 4: ajuste do modelo
Agora, precisamos ajustar o modelo aos seus dados. Isso pode ser feito chamando o método fit () da instância do modelo.
Etapa 5: Aplicar o modelo
Depois de ajustar o modelo, podemos aplicá-lo a novos dados. Para aprendizagem supervisionada, usepredict()método para prever os rótulos de dados desconhecidos. Enquanto para aprendizagem não supervisionada, usepredict() ou transform() para inferir propriedades dos dados.
Exemplo de aprendizagem supervisionada
Aqui, como exemplo deste processo, estamos tomando o caso comum de ajustar uma linha aos dados (x, y), ou seja simple linear regression.
Primeiro, precisamos carregar o conjunto de dados, estamos usando o conjunto de dados iris -
Exemplo
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shapeResultado
(150, 4)Exemplo
y_iris = iris['species']
y_iris.shapeResultado
(150,)Exemplo
Agora, para este exemplo de regressão, vamos usar os seguintes dados de amostra -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);Resultado
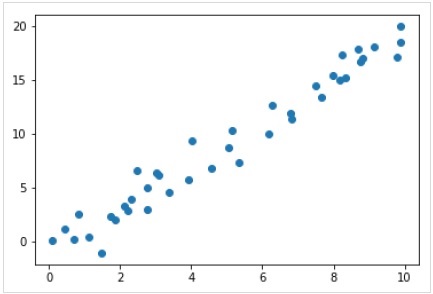
Portanto, temos os dados acima para nosso exemplo de regressão linear.
Agora, com esses dados, podemos aplicar as etapas acima mencionadas.
Escolha uma classe de modelo
Aqui, para calcular um modelo de regressão linear simples, precisamos importar a classe de regressão linear da seguinte forma -
from sklearn.linear_model import LinearRegressionEscolha os hiperparâmetros do modelo
Depois de escolher uma classe de modelo, precisamos fazer algumas escolhas importantes, que geralmente são representadas como hiperparâmetros ou os parâmetros que devem ser definidos antes que o modelo seja ajustado aos dados. Aqui, para este exemplo de regressão linear, gostaríamos de ajustar a interceptação usando ofit_intercept hiperparâmetro da seguinte forma -
Example
model = LinearRegression(fit_intercept = True)
modelOutput
LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None, normalize = False)Organizando os dados
Agora, como sabemos que nossa variável alvo y está na forma correta, ou seja, um comprimento n_samplesmatriz de 1-D. Mas, precisamos remodelar a matriz de recursosX para torná-lo uma matriz de tamanho [n_samples, n_features]. Isso pode ser feito da seguinte forma -
Example
X = x[:, np.newaxis]
X.shapeOutput
(40, 1)Ajuste do modelo
Depois de organizar os dados, é hora de ajustar o modelo, ou seja, aplicar nosso modelo aos dados. Isso pode ser feito com a ajuda defit() método da seguinte forma -
Example
model.fit(X, y)Output
LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None,normalize = False)No Scikit-learn, o fit() processo tem alguns sublinhados à direita.
Para este exemplo, o parâmetro abaixo mostra a inclinação do ajuste linear simples dos dados -
Example
model.coef_Output
array([1.99839352])O parâmetro abaixo representa a interceptação do ajuste linear simples aos dados -
Example
model.intercept_Output
-0.9895459457775022Aplicando o modelo a novos dados
Depois de treinar o modelo, podemos aplicá-lo a novos dados. Como a principal tarefa do aprendizado de máquina supervisionado é avaliar o modelo com base em novos dados que não fazem parte do conjunto de treinamento. Isso pode ser feito com a ajuda depredict() método da seguinte forma -
Example
xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);Output
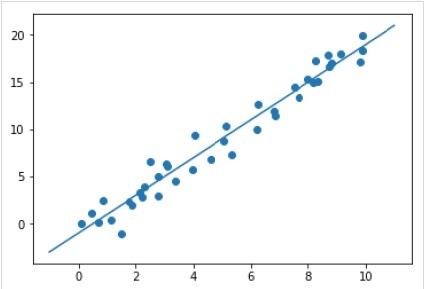
Exemplo completo de trabalho / executável
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model
X = x[:, np.newaxis]
X.shape
model.fit(X, y)
model.coef_
model.intercept_
xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);Exemplo de aprendizado não supervisionado
Aqui, como exemplo desse processo, estamos tomando um caso comum de redução da dimensionalidade do conjunto de dados Iris para que possamos visualizá-lo com mais facilidade. Para este exemplo, vamos usar a análise de componentes principais (PCA), uma técnica de redução de dimensionalidade linear rápida.
Como no exemplo acima, podemos carregar e plotar os dados aleatórios do conjunto de dados da íris. Depois disso, podemos seguir as etapas abaixo -
Escolha uma classe de modelo
from sklearn.decomposition import PCAEscolha os hiperparâmetros do modelo
Example
model = PCA(n_components=2)
modelOutput
PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
svd_solver = 'auto', tol = 0.0, whiten = False)Ajuste do modelo
Example
model.fit(X_iris)Output
PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
svd_solver = 'auto', tol = 0.0, whiten = False)Transforme os dados em bidimensionais
Example
X_2D = model.transform(X_iris)Agora, podemos plotar o resultado da seguinte maneira -
Output
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue = 'species', data = iris, fit_reg = False);Output
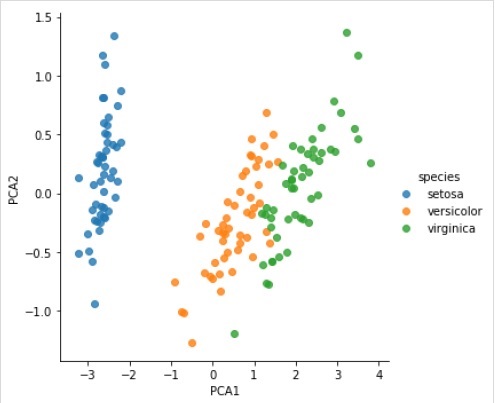
Exemplo completo de trabalho / executável
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.decomposition import PCA
model = PCA(n_components=2)
model
model.fit(X_iris)
X_2D = model.transform(X_iris)
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False);Os objetos do Scikit-learn compartilham uma API básica uniforme que consiste nas três interfaces complementares a seguir -
Estimator interface - É para construir e ajustar os modelos.
Predictor interface - É para fazer previsões.
Transformer interface - É para converter dados.
As APIs adotam convenções simples e as escolhas de design foram guiadas de maneira a evitar a proliferação de código de estrutura.
Objetivo das Convenções
O objetivo das convenções é garantir que a API siga os seguintes princípios gerais -
Consistency - Todos os objetos, sejam eles básicos ou compostos, devem compartilhar uma interface consistente que é composta por um conjunto limitado de métodos.
Inspection - Os parâmetros do construtor e os valores dos parâmetros determinados pelo algoritmo de aprendizagem devem ser armazenados e expostos como atributos públicos.
Non-proliferation of classes - Os conjuntos de dados devem ser representados como matrizes NumPy ou matriz esparsa Scipy, enquanto os nomes e valores de hiperparâmetros devem ser representados como strings Python padrão para evitar a proliferação de código de estrutura.
Composition - Os algoritmos, quer sejam expressos como sequências ou combinações de transformações dos dados ou naturalmente vistos como meta-algoritmos parametrizados em outros algoritmos, devem ser implementados e compostos a partir de blocos de construção existentes.
Sensible defaults- No scikit-learn, sempre que uma operação requer um parâmetro definido pelo usuário, um valor padrão apropriado é definido. Este valor padrão deve fazer com que a operação seja executada de forma sensata, por exemplo, fornecendo uma solução de linha de base para a tarefa em questão.
Várias Convenções
As convenções disponíveis no Sklearn são explicadas abaixo -
Fundição de tipo
Ele afirma que a entrada deve ser convertida para float64. No exemplo a seguir, em quesklearn.random_projection módulo usado para reduzir a dimensionalidade dos dados, irá explicá-lo -
Example
import numpy as np
from sklearn import random_projection
rannge = np.random.RandomState(0)
X = range.rand(10,2000)
X = np.array(X, dtype = 'float32')
X.dtype
Transformer_data = random_projection.GaussianRandomProjection()
X_new = transformer.fit_transform(X)
X_new.dtypeOutput
dtype('float32')
dtype('float64')No exemplo acima, podemos ver que X é float32 que é lançado para float64 de fit_transform(X).
Parâmetros de reajuste e atualização
Os hiperparâmetros de um estimador podem ser atualizados e reajustados após ter sido construído por meio do set_params()método. Vamos ver o seguinte exemplo para entender isso -
Example
import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])Output
array([0, 0, 0, 0, 0])Uma vez que o estimador foi construído, o código acima mudará o kernel padrão rbf para linear via SVC.set_params().
Agora, o código a seguir mudará de volta o kernel para rbf para reajustar o estimador e fazer uma segunda previsão.
Example
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])Output
array([0, 0, 0, 0, 0])Código completo
A seguir está o programa executável completo -
import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])Adaptação multiclasse e etiqueta múltipla
No caso de ajuste de várias classes, tanto as tarefas de aprendizado quanto as de previsão dependem do formato dos dados do alvo ajustados. O módulo usado ésklearn.multiclass. Verifique o exemplo abaixo, onde o classificador multiclasse se ajusta a uma matriz 1d.
Example
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = [0, 0, 1, 1, 2]
classif = OneVsRestClassifier(estimator = SVC(gamma = 'scale',random_state = 0))
classif.fit(X, y).predict(X)Output
array([0, 0, 1, 1, 2])No exemplo acima, o classificador é ajustado em uma matriz dimensional de rótulos multiclasse e o predict()método, portanto, fornece previsão multiclasse correspondente. Mas, por outro lado, também é possível ajustar em uma matriz bidimensional de indicadores de rótulo binários da seguinte maneira -
Example
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = LabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)Output
array(
[
[0, 0, 0],
[0, 0, 0],
[0, 1, 0],
[0, 1, 0],
[0, 0, 0]
]
)Da mesma forma, no caso de ajuste de múltiplas etiquetas, uma instância pode receber várias etiquetas da seguinte forma -
Example
from sklearn.preprocessing import MultiLabelBinarizer
y = [[0, 1], [0, 2], [1, 3], [0, 2, 3], [2, 4]]
y = MultiLabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)Output
array(
[
[1, 0, 1, 0, 0],
[1, 0, 1, 0, 0],
[1, 0, 1, 1, 0],
[1, 0, 1, 1, 0],
[1, 0, 1, 0, 0]
]
)No exemplo acima, sklearn.MultiLabelBinarizeré usado para binarizar a matriz bidimensional de rótulos múltiplos para ajustar. É por isso que a função predict () fornece uma matriz 2d como saída com vários rótulos para cada instância.
Este capítulo o ajudará a aprender sobre a modelagem linear no Scikit-Learn. Vamos começar entendendo o que é regressão linear no Sklearn.
A tabela a seguir lista vários modelos lineares fornecidos pela Scikit-Learn -
| Sr. Não | Modelo e descrição |
|---|---|
| 1 | Regressão linear É um dos melhores modelos estatísticos que estuda a relação entre uma variável dependente (Y) com um determinado conjunto de variáveis independentes (X). |
| 2 | Regressão Logística A regressão logística, apesar do nome, é um algoritmo de classificação e não um algoritmo de regressão. Com base em um determinado conjunto de variáveis independentes, é usado para estimar o valor discreto (0 ou 1, sim / não, verdadeiro / falso). |
| 3 | Ridge Regression A regressão de cume ou regularização de Tikhonov é a técnica de regularização que realiza a regularização de L2. Ele modifica a função de perda adicionando a penalidade (quantidade de encolhimento) equivalente ao quadrado da magnitude dos coeficientes. |
| 4 | Regressão Bayesian Ridge A regressão bayesiana permite que um mecanismo natural sobreviva a dados insuficientes ou dados mal distribuídos, formulando a regressão linear usando distribuidores de probabilidade em vez de estimativas pontuais. |
| 5 | LAÇO LASSO é a técnica de regularização que realiza a regularização L1. Ele modifica a função de perda adicionando a penalidade (quantidade de encolhimento) equivalente à soma do valor absoluto dos coeficientes. |
| 6 | LASSO multi-tarefa Ele permite ajustar vários problemas de regressão em conjunto, fazendo com que os recursos selecionados sejam os mesmos para todos os problemas de regressão, também chamados de tarefas. Sklearn fornece um modelo linear denominado MultiTaskLasso, treinado com uma norma mista L1, L2 para regularização, que estima coeficientes esparsos para problemas de regressão múltipla em conjunto. |
| 7 | Elastic-Net O Elastic-Net é um método de regressão regularizado que combina linearmente ambas as penalidades, ou seja, L1 e L2 dos métodos de regressão Lasso e Ridge. É útil quando há vários recursos correlacionados. |
| 8 | Rede Elástica Multitarefa É um modelo Elastic-Net que permite ajustar vários problemas de regressão em conjunto, fazendo com que os recursos selecionados sejam os mesmos para todos os problemas de regressão, também chamados de tarefas |
Este capítulo enfoca os recursos polinomiais e ferramentas de pipelining no Sklearn.
Introdução aos recursos polinomiais
Modelos lineares treinados em funções não lineares de dados geralmente mantêm o desempenho rápido dos métodos lineares. Também permite que eles se ajustem a uma gama muito mais ampla de dados. Essa é a razão pela qual no aprendizado de máquina esses modelos lineares, que são treinados em funções não lineares, são usados.
Um exemplo é que uma regressão linear simples pode ser estendida pela construção de recursos polinomiais a partir dos coeficientes.
Matematicamente, suponha que temos um modelo de regressão linear padrão, então para dados 2-D ficaria assim -
$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}$$Agora, podemos combinar os recursos em polinômios de segunda ordem e nosso modelo se parecerá com o seguinte -
$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{1}X_{2}+W_{4}X_1^2+W_{5}X_2^2$$O acima ainda é um modelo linear. Aqui, vimos que a regressão polinomial resultante está na mesma classe de modelos lineares e pode ser resolvida de forma semelhante.
Para fazer isso, o scikit-learn oferece um módulo chamado PolynomialFeatures. Este módulo transforma uma matriz de dados de entrada em uma nova matriz de dados de determinado grau.
Parâmetros
A tabela a seguir consiste nos parâmetros usados por PolynomialFeatures módulo
| Sr. Não | Parâmetro e Descrição |
|---|---|
| 1 | degree - inteiro, padrão = 2 Ele representa o grau dos recursos polinomiais. |
| 2 | interaction_only - Booleano, padrão = falso Por padrão, é falso, mas se definido como verdadeiro, os recursos que são produtos de recursos de entrada de muitos graus distintos são produzidos. Esses recursos são chamados de recursos de interação. |
| 3 | include_bias - Booleano, padrão = verdadeiro Inclui uma coluna de polarização, ou seja, o recurso em que todas as potências de polinômios são zero. |
| 4 | order - str em {'C', 'F'}, padrão = 'C' Este parâmetro representa a ordem da matriz de saída no caso denso. A ordem 'F' significa mais rápido para calcular, mas por outro lado, pode desacelerar estimadores subsequentes. |
Atributos
A tabela a seguir consiste nos atributos usados por PolynomialFeatures módulo
| Sr. Não | Atributos e descrição |
|---|---|
| 1 | powers_ - matriz, forma (n_output_features, n_input_features) Mostra que powers_ [i, j] é o expoente da j-ésima entrada na i-ésima saída. |
| 2 | n_input_features _ - int Como o nome sugere, ele fornece o número total de recursos de entrada. |
| 3 | n_output_features _ - int Como o nome sugere, ele fornece o número total de recursos de saída polinomial. |
Exemplo de Implementação
O seguinte script Python usa PolynomialFeatures transformador para transformar matriz de 8 em forma (4,2) -
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
Y = np.arange(8).reshape(4, 2)
poly = PolynomialFeatures(degree=2)
poly.fit_transform(Y)Resultado
array(
[
[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.],
[ 1., 6., 7., 36., 42., 49.]
]
)Racionalizando usando ferramentas Pipeline
O tipo de pré-processamento acima, ou seja, transformar uma matriz de dados de entrada em uma nova matriz de dados de um determinado grau, pode ser simplificado com o Pipeline ferramentas, que são basicamente usadas para encadear vários estimadores em um.
Exemplo
Os scripts python abaixo usando as ferramentas Pipeline do Scikit-learn para agilizar o pré-processamento (caberão em dados polinomiais de ordem 3).
#First, import the necessary packages.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np
#Next, create an object of Pipeline tool
Stream_model = Pipeline([('poly', PolynomialFeatures(degree=3)), ('linear', LinearRegression(fit_intercept=False))])
#Provide the size of array and order of polynomial data to fit the model.
x = np.arange(5)
y = 3 - 2 * x + x ** 2 - x ** 3
Stream_model = model.fit(x[:, np.newaxis], y)
#Calculate the input polynomial coefficients.
Stream_model.named_steps['linear'].coef_Resultado
array([ 3., -2., 1., -1.])A saída acima mostra que o modelo linear treinado em recursos polinomiais é capaz de recuperar os coeficientes polinomiais de entrada exatos.
Aqui, aprenderemos sobre um algoritmo de otimização no Sklearn, denominado Stochastic Gradient Descent (SGD).
Stochastic Gradient Descent (SGD) é um algoritmo de otimização simples, mas eficiente, usado para encontrar os valores de parâmetros / coeficientes de funções que minimizam uma função de custo. Em outras palavras, é usado para aprendizagem discriminativa de classificadores lineares sob funções de perda convexa, como SVM e regressão logística. Ele foi aplicado com sucesso a conjuntos de dados em grande escala porque a atualização dos coeficientes é realizada para cada instância de treinamento, e não no final das instâncias.
Classificador SGD
O classificador Stochastic Gradient Descent (SGD) basicamente implementa uma rotina de aprendizagem SGD simples, suportando várias funções de perda e penalidades para a classificação. Scikit-learn forneceSGDClassifier módulo para implementar a classificação SGD.
Parâmetros
A tabela a seguir consiste nos parâmetros usados por SGDClassifier módulo -
| Sr. Não | Parâmetro e Descrição |
|---|---|
| 1 | loss - str, default = 'dobradiça' Ele representa a função de perda a ser usada durante a implementação. O valor padrão é 'dobradiça', o que nos dará um SVM linear. As outras opções que podem ser usadas são -
|
| 2 | penalty - str, 'nenhum', 'l2', 'l1', 'elasticnet' É o termo de regularização usado no modelo. Por padrão, é L2. Podemos usar L1 ou 'elasticnet; também, mas ambos podem trazer esparsidade para o modelo, portanto, não alcançável com L2. |
| 3 | alpha - flutuante, padrão = 0,0001 Alpha, a constante que multiplica o termo de regularização, é o parâmetro de ajuste que decide o quanto queremos penalizar o modelo. O valor padrão é 0,0001. |
| 4 | l1_ratio - flutuante, padrão = 0,15 Isso é chamado de parâmetro de mistura ElasticNet. Seu intervalo é 0 <= l1_ratio <= 1. Se l1_ratio = 1, a penalidade seria a penalidade de L1. Se l1_ratio = 0, a penalidade seria uma penalidade L2. |
| 5 | fit_intercept - Booleano, padrão = verdadeiro Este parâmetro especifica que uma constante (polarização ou interceptação) deve ser adicionada à função de decisão. Nenhuma interceptação será usada no cálculo e os dados serão considerados já centrados, se forem configurados como falsos. |
| 6 | tol - flutuante ou nenhum, opcional, padrão = 1.e-3 Este parâmetro representa o critério de parada para iterações. Seu valor padrão é False, mas se definido como Nenhum, as iterações irão parar quandoloss > best_loss - tol for n_iter_no_changeépocas sucessivas. |
| 7 | shuffle - Booleano, opcional, padrão = Verdadeiro Este parâmetro representa se queremos que nossos dados de treinamento sejam misturados após cada época ou não. |
| 8 | verbose - inteiro, padrão = 0 Ele representa o nível de verbosidade. Seu valor padrão é 0. |
| 9 | epsilon - flutuante, padrão = 0,1 Este parâmetro especifica a largura da região insensível. Se perda = 'insensível a epsilon', qualquer diferença, entre a previsão atual e o rótulo correto, menor que o limite seria ignorada. |
| 10 | max_iter - int, opcional, padrão = 1000 Como o nome sugere, ele representa o número máximo de passagens ao longo das épocas, ou seja, dados de treinamento. |
| 11 | warm_start - bool, opcional, padrão = falso Com este parâmetro definido como True, podemos reutilizar a solução da chamada anterior para caber como inicialização. Se escolhermos o padrão, ou seja, falso, ele apagará a solução anterior. |
| 12 | random_state - int, instância RandomState ou Nenhum, opcional, padrão = nenhum Este parâmetro representa a semente do número pseudoaleatório gerado que é usado ao embaralhar os dados. A seguir estão as opções.
|
| 13 | n_jobs - int ou nenhum, opcional, padrão = nenhum Representa o número de CPUs a serem usadas na computação OVA (One Versus All), para problemas de várias classes. O valor padrão é nenhum, o que significa 1. |
| 14 | learning_rate - string, opcional, padrão = 'ideal'
|
| 15 | eta0 - duplo, padrão = 0,0 Representa a taxa de aprendizado inicial para as opções de taxa de aprendizado mencionadas acima, ou seja, 'constante', 'invscalling' ou 'adaptável'. |
| 16 | power_t - iduplo, padrão = 0,5 É o expoente para a taxa de aprendizagem "crescente". |
| 17 | early_stopping - bool, padrão = False Este parâmetro representa o uso de parada antecipada para encerrar o treinamento quando a pontuação de validação não está melhorando. Seu valor padrão é falso, mas quando definido como verdadeiro, ele automaticamente separa uma fração estratificada dos dados de treinamento como validação e interrompe o treinamento quando a pontuação de validação não está melhorando. |
| 18 | validation_fraction - flutuante, padrão = 0,1 Só é usado quando a parada precoce é verdadeira. Representa a proporção de dados de treinamento a serem definidos como validação definida para o encerramento antecipado de dados de treinamento. |
| 19 | n_iter_no_change - int, padrão = 5 Ele representa o número de iterações sem melhorias, caso o algoritmo seja executado antes da parada antecipada. |
| 20 | classs_weight - dict, {class_label: weight} ou “balanceado”, ou nenhum, opcional Este parâmetro representa os pesos associados às classes. Se não forem fornecidas, as classes devem ter peso 1. |
| 20 | warm_start - bool, opcional, padrão = falso Com este parâmetro definido como True, podemos reutilizar a solução da chamada anterior para caber como inicialização. Se escolhermos o padrão, ou seja, falso, ele apagará a solução anterior. |
| 21 | average - iBoolean ou int, opcional, default = false Representa o número de CPUs a serem usadas na computação OVA (One Versus All), para problemas de várias classes. O valor padrão é nenhum, o que significa 1. |
Atributos
A tabela a seguir consiste nos atributos usados por SGDClassifier módulo -
| Sr. Não | Atributos e descrição |
|---|---|
| 1 | coef_ - array, shape (1, n_features) if n_classes == 2, else (n_classes, n_features) Este atributo fornece o peso atribuído aos recursos. |
| 2 | intercept_ - matriz, forma (1,) se n_classes == 2, senão (n_classes,) Ele representa o termo independente na função de decisão. |
| 3 | n_iter_ - int Fornece o número de iterações para atingir o critério de parada. |
Implementation Example
Como outros classificadores, Stochastic Gradient Descent (SGD) deve ser equipado com as seguintes duas matrizes -
Um array X contendo as amostras de treinamento. É do tamanho [n_samples, n_features].
Uma matriz Y contendo os valores alvo, ou seja, rótulos de classe para as amostras de treinamento. É do tamanho [n_samples].
Example
O script Python a seguir usa o modelo linear SGDClassifier -
import numpy as np
from sklearn import linear_model
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
Y = np.array([1, 1, 2, 2])
SGDClf = linear_model.SGDClassifier(max_iter = 1000, tol=1e-3,penalty = "elasticnet")
SGDClf.fit(X, Y)Output
SGDClassifier(
alpha = 0.0001, average = False, class_weight = None,
early_stopping = False, epsilon = 0.1, eta0 = 0.0, fit_intercept = True,
l1_ratio = 0.15, learning_rate = 'optimal', loss = 'hinge', max_iter = 1000,
n_iter = None, n_iter_no_change = 5, n_jobs = None, penalty = 'elasticnet',
power_t = 0.5, random_state = None, shuffle = True, tol = 0.001,
validation_fraction = 0.1, verbose = 0, warm_start = False
)Example
Agora, uma vez ajustado, o modelo pode prever novos valores da seguinte forma -
SGDClf.predict([[2.,2.]])Output
array([2])Example
Para o exemplo acima, podemos obter o vetor de peso com a ajuda do seguinte script python -
SGDClf.coef_Output
array([[19.54811198, 9.77200712]])Example
Da mesma forma, podemos obter o valor de interceptar com a ajuda do seguinte script python -
SGDClf.intercept_Output
array([10.])Example
Podemos obter a distância sinalizada para o hiperplano usando SGDClassifier.decision_function como usado no seguinte script python -
SGDClf.decision_function([[2., 2.]])Output
array([68.6402382])Regressor SGD
O regressor Stochastic Gradient Descent (SGD) basicamente implementa uma rotina de aprendizagem SGD simples que suporta várias funções de perda e penalidades para ajustar modelos de regressão linear. Scikit-learn forneceSGDRegressor módulo para implementar a regressão SGD.
Parâmetros
Parâmetros usados por SGDRegressorsão quase os mesmos que foram usados no módulo SGDClassifier. A diferença está no parâmetro 'perda'. ParaSGDRegressor parâmetro de perda dos módulos, os valores positivos são os seguintes -
squared_loss - Refere-se ao ajuste de mínimos quadrados ordinários.
huber: SGDRegressor- corrigir os outliers mudando de perda quadrada para linear após uma distância de épsilon. O trabalho de 'huber' é modificar 'squared_loss' para que o algoritmo se concentre menos na correção de outliers.
epsilon_insensitive - Na verdade, ele ignora os erros menores que épsilon.
squared_epsilon_insensitive- É o mesmo que epsilon_insensitive. A única diferença é que se torna a perda quadrática após a tolerância de épsilon.
Outra diferença é que o parâmetro denominado 'power_t' tem o valor padrão de 0,25 em vez de 0,5 como em SGDClassifier. Além disso, ele não possui os parâmetros 'class_weight' e 'n_jobs'.
Atributos
Os atributos de SGDRegressor também são iguais aos do módulo SGDClassifier. Em vez disso, tem três atributos extras como segue -
average_coef_ - matriz, forma (n_features,)
Como o nome sugere, ele fornece os pesos médios atribuídos aos recursos.
average_intercept_ - matriz, forma (1,)
Como o nome sugere, ele fornece o termo médio de interceptação.
t_ - int
Ele fornece o número de atualizações de peso realizadas durante a fase de treinamento.
Note - os atributos average_coef_ e average_intercept_ funcionarão após habilitar o parâmetro 'average' para True.
Implementation Example
O seguinte script Python usa SGDRegressor modelo linear -
import numpy as np
from sklearn import linear_model
n_samples, n_features = 10, 5
rng = np.random.RandomState(0)
y = rng.randn(n_samples)
X = rng.randn(n_samples, n_features)
SGDReg =linear_model.SGDRegressor(
max_iter = 1000,penalty = "elasticnet",loss = 'huber',tol = 1e-3, average = True
)
SGDReg.fit(X, y)Output
SGDRegressor(
alpha = 0.0001, average = True, early_stopping = False, epsilon = 0.1,
eta0 = 0.01, fit_intercept = True, l1_ratio = 0.15,
learning_rate = 'invscaling', loss = 'huber', max_iter = 1000,
n_iter = None, n_iter_no_change = 5, penalty = 'elasticnet', power_t = 0.25,
random_state = None, shuffle = True, tol = 0.001, validation_fraction = 0.1,
verbose = 0, warm_start = False
)Example
Agora, uma vez ajustado, podemos obter o vetor de peso com a ajuda do seguinte script python -
SGDReg.coef_Output
array([-0.00423314, 0.00362922, -0.00380136, 0.00585455, 0.00396787])Example
Da mesma forma, podemos obter o valor de interceptar com a ajuda do seguinte script python -
SGReg.intercept_Output
SGReg.intercept_Example
Podemos obter o número de atualizações de peso durante a fase de treinamento com a ajuda do seguinte script python -
SGDReg.t_Output
61.0Prós e Contras do SGD
Seguindo os prós do SGD -
Stochastic Gradient Descent (SGD) é muito eficiente.
É muito fácil de implementar, pois há muitas oportunidades para ajuste de código.
Seguindo os contras do SGD -
Stochastic Gradient Descent (SGD) requer vários hiperparâmetros como parâmetros de regularização.
É sensível ao dimensionamento de recursos.
Este capítulo trata de um método de aprendizado de máquina denominado Support Vector Machines (SVMs).
Introdução
As máquinas de vetores de suporte (SVMs) são métodos de aprendizado de máquina supervisionados poderosos, porém flexíveis, usados para classificação, regressão e detecção de outliers. SVMs são muito eficientes em espaços dimensionais elevados e geralmente são usados em problemas de classificação. Os SVMs são populares e têm memória eficiente porque usam um subconjunto de pontos de treinamento na função de decisão.
O principal objetivo dos SVMs é dividir os conjuntos de dados em várias classes, a fim de encontrar um maximum marginal hyperplane (MMH) o que pode ser feito nas duas etapas a seguir -
O Support Vector Machines primeiro irá gerar hiperplanos iterativamente que separam as classes da melhor maneira.
Depois disso, ele vai escolher o hiperplano que segregará as classes corretamente.
Alguns conceitos importantes em SVM são os seguintes -
Support Vectors- Eles podem ser definidos como os pontos de dados mais próximos do hiperplano. Os vetores de suporte ajudam a decidir a linha de separação.
Hyperplane - O plano ou espaço de decisão que divide o conjunto de objetos de diferentes classes.
Margin - A lacuna entre duas linhas nos pontos de dados do armário de classes diferentes é chamada de margem.
Os diagramas a seguir darão uma ideia sobre esses conceitos de SVM -
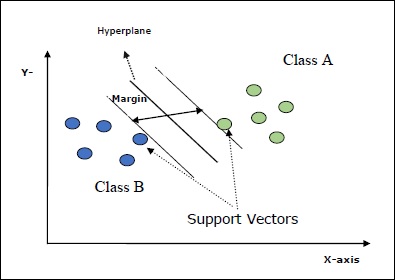
O SVM no Scikit-learn oferece suporte a vetores de amostra esparsos e densos como entrada.
Classificação de SVM
Scikit-learn oferece três classes, a saber SVC, NuSVC e LinearSVC que pode realizar a classificação multiclasse.
SVC
É a classificação do vetor C-suporte, cuja implementação é baseada em libsvm. O módulo usado pelo scikit-learn ésklearn.svm.SVC. Esta classe lida com o suporte multiclasse de acordo com o esquema um contra um.
Parâmetros
A tabela a seguir consiste nos parâmetros usados por sklearn.svm.SVC classe -
| Sr. Não | Parâmetro e Descrição |
|---|---|
| 1 | C - flutuante, opcional, padrão = 1,0 É o parâmetro de penalidade do termo de erro. |
| 2 | kernel - string, opcional, padrão = 'rbf' Este parâmetro especifica o tipo de kernel a ser usado no algoritmo. podemos escolher qualquer um entre,‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’. O valor padrão do kernel seria‘rbf’. |
| 3 | degree - int, opcional, padrão = 3 Ele representa o grau da função 'poli' do kernel e será ignorado por todos os outros kernels. |
| 4 | gamma - {'escala', 'auto'} ou flutuação, É o coeficiente de kernel para os kernels 'rbf', 'poly' e 'sigmoid'. |
| 5 | optinal default - = 'escala' Se você escolher o padrão, ou seja, gama = 'escala', então o valor de gama a ser usado pelo SVC é 1 / (_ ∗. ()). Por outro lado, se gamma = 'auto', ele usa 1 / _. |
| 6 | coef0 - flutuante, opcional, padrão = 0,0 Um termo independente na função do kernel que só é significativo em 'poli' e 'sigmóide'. |
| 7 | tol - flutuante, opcional, padrão = 1.e-3 Este parâmetro representa o critério de parada para iterações. |
| 8 | shrinking - Booleano, opcional, padrão = Verdadeiro Este parâmetro representa se queremos usar uma heurística de redução ou não. |
| 9 | verbose - Booleano, padrão: falso Ele ativa ou desativa a saída detalhada. Seu valor padrão é falso. |
| 10 | probability - booleano, opcional, padrão = verdadeiro Este parâmetro ativa ou desativa as estimativas de probabilidade. O valor padrão é falso, mas deve ser habilitado antes de chamarmos o ajuste. |
| 11 | max_iter - int, opcional, padrão = -1 Como o nome sugere, ele representa o número máximo de iterações no solucionador. O valor -1 significa que não há limite para o número de iterações. |
| 12 | cache_size - float, opcional Este parâmetro irá especificar o tamanho do cache do kernel. O valor será em MB (MegaBytes). |
| 13 | random_state - int, instância RandomState ou Nenhum, opcional, padrão = nenhum Este parâmetro representa a semente do número pseudoaleatório gerado que é usado ao embaralhar os dados. A seguir estão as opções -
|
| 14 | class_weight - {dict, 'balanceado'}, opcional Este parâmetro definirá o parâmetro C da classe j para _ℎ [] ∗ para SVC. Se usarmos a opção padrão, significa que todas as classes devem ter peso um. Por outro lado, se você escolherclass_weight:balanced, ele usará os valores de y para ajustar automaticamente os pesos. |
| 15 | decision_function_shape - ovo ',' ovr ', padrão =' ovr ' Este parâmetro decidirá se o algoritmo retornará ‘ovr’ (um vs resto) função de decisão de forma como todos os outros classificadores, ou o original ovo(um contra um) função de decisão de libsvm. |
| 16 | break_ties - booleano, opcional, padrão = falso True - A previsão quebrará empates de acordo com os valores de confiança de função_de_decisão False - O prognóstico retornará a primeira turma entre as turmas empatadas. |
Atributos
A tabela a seguir consiste nos atributos usados por sklearn.svm.SVC classe -
| Sr. Não | Atributos e descrição |
|---|---|
| 1 | support_ - semelhante a matriz, forma = [n_SV] Ele retorna os índices dos vetores de suporte. |
| 2 | support_vectors_ - semelhante a matriz, forma = [n_SV, n_features] Ele retorna os vetores de suporte. |
| 3 | n_support_ - semelhante a matriz, dtype = int32, forma = [n_class] Ele representa o número de vetores de suporte para cada classe. |
| 4 | dual_coef_ - matriz, forma = [n_class-1, n_SV] Estes são os coeficientes dos vetores de suporte na função de decisão. |
| 5 | coef_ - matriz, forma = [n_class * (n_class-1) / 2, n_features] Este atributo, disponível apenas no caso de kernel linear, fornece o peso atribuído aos recursos. |
| 6 | intercept_ - matriz, forma = [n_class * (n_class-1) / 2] Representa o termo independente (constante) na função de decisão. |
| 7 | fit_status_ - int A saída seria 0 se estiver corretamente ajustada. A saída seria 1 se fosse ajustada incorretamente. |
| 8 | classes_ - matriz de forma = [n_classes] Dá os rótulos das classes. |
Implementation Example
Como outros classificadores, o SVC também deve ser equipado com as duas seguintes matrizes -
Uma matriz Xsegurando as amostras de treinamento. É do tamanho [n_samples, n_features].
Uma matriz Ymantendo os valores alvo, ou seja, rótulos de classe para os exemplos de treinamento. É do tamanho [n_samples].
O seguinte script Python usa sklearn.svm.SVC classe -
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import SVC
SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
SVCClf.fit(X, y)Output
SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0,
decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
max_iter = -1, probability = False, random_state = None, shrinking = False,
tol = 0.001, verbose = False)Example
Agora, uma vez ajustado, podemos obter o vetor de peso com a ajuda do seguinte script python -
SVCClf.coef_Output
array([[0.5, 0.5]])Example
Da mesma forma, podemos obter o valor de outros atributos da seguinte maneira -
SVCClf.predict([[-0.5,-0.8]])Output
array([1])Example
SVCClf.n_support_Output
array([1, 1])Example
SVCClf.support_vectors_Output
array(
[
[-1., -1.],
[ 1., 1.]
]
)Example
SVCClf.support_Output
array([0, 2])Example
SVCClf.intercept_Output
array([-0.])Example
SVCClf.fit_status_Output
0NuSVC
NuSVC é Nu Support Vector Classification. É outra classe fornecida pelo scikit-learn que pode realizar a classificação de várias classes. É como o SVC, mas o NuSVC aceita conjuntos de parâmetros ligeiramente diferentes. O parâmetro que é diferente de SVC é o seguinte -
nu - flutuante, opcional, padrão = 0,5
Ele representa um limite superior da fração de erros de treinamento e um limite inferior da fração de vetores de suporte. Seu valor deve estar no intervalo de (o, 1].
O resto dos parâmetros e atributos são os mesmos do SVC.
Exemplo de Implementação
Podemos implementar o mesmo exemplo usando sklearn.svm.NuSVC classe também.
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import NuSVC
NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
NuSVCClf.fit(X, y)Resultado
NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0,
decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
max_iter = -1, nu = 0.5, probability = False, random_state = None,
shrinking = False, tol = 0.001, verbose = False)Podemos obter as saídas do restante dos atributos, como no caso do SVC.
LinearSVC
É a classificação do vetor de suporte linear. É semelhante ao SVC com kernel = 'linear'. A diferença entre eles é queLinearSVC implementado em termos de liblinear enquanto SVC é implementado em libsvm. Essa é a razãoLinearSVCtem mais flexibilidade na escolha de penalidades e funções de perda. Também é melhor dimensionado para um grande número de amostras.
Se falarmos sobre seus parâmetros e atributos, então ele não suporta ‘kernel’ porque é considerado linear e também carece de alguns dos atributos como support_, support_vectors_, n_support_, fit_status_ e, dual_coef_.
No entanto, ele suporta penalty e loss parâmetros como segue -
penalty − string, L1 or L2(default = ‘L2’)
Este parâmetro é usado para especificar a norma (L1 ou L2) usada na penalização (regularização).
loss − string, hinge, squared_hinge (default = squared_hinge)
Ele representa a função de perda, em que 'dobradiça' é a perda padrão de SVM e 'quadratura_valor' é o quadrado da perda de dobradiça.
Exemplo de Implementação
O seguinte script Python usa sklearn.svm.LinearSVC classe -
from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
X, y = make_classification(n_features = 4, random_state = 0)
LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5)
LSVCClf.fit(X, y)Resultado
LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True,
intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000,
multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)Exemplo
Agora, uma vez ajustado, o modelo pode prever novos valores da seguinte forma -
LSVCClf.predict([[0,0,0,0]])Resultado
[1]Exemplo
Para o exemplo acima, podemos obter o vetor de peso com a ajuda do seguinte script python -
LSVCClf.coef_Resultado
[[0. 0. 0.91214955 0.22630686]]Exemplo
Da mesma forma, podemos obter o valor de interceptar com a ajuda do seguinte script python -
LSVCClf.intercept_Resultado
[0.26860518]Regressão com SVM
Conforme discutido anteriormente, o SVM é usado para problemas de classificação e regressão. O método de classificação de vetores de suporte (SVC) do Scikit-learn pode ser estendido para resolver problemas de regressão também. Esse método estendido é denominado Support Vector Regression (SVR).
Semelhança básica entre SVM e SVR
O modelo criado pelo SVC depende apenas de um subconjunto de dados de treinamento. Por quê? Porque a função de custo para construir o modelo não se preocupa com pontos de dados de treinamento que estão fora da margem.
Visto que o modelo produzido pelo SVR (Support Vector Regression) também depende apenas de um subconjunto dos dados de treinamento. Por quê? Porque a função de custo para construir o modelo ignora quaisquer pontos de dados de treinamento próximos à previsão do modelo.
Scikit-learn oferece três classes, a saber SVR, NuSVR and LinearSVR como três implementações diferentes de SVR.
SVR
É a regressão vetorial de suporte a Epsilon, cuja implementação é baseada em libsvm. Em oposição aSVC Existem dois parâmetros livres no modelo, a saber ‘C’ e ‘epsilon’.
epsilon - flutuante, opcional, padrão = 0,1
Ele representa o épsilon no modelo SVR-épsilon e especifica o tubo épsilon dentro do qual nenhuma penalidade está associada na função de perda de treinamento com pontos previstos dentro de uma distância épsilon do valor real.
O resto dos parâmetros e atributos são semelhantes aos usados em SVC.
Exemplo de Implementação
O seguinte script Python usa sklearn.svm.SVR classe -
from sklearn import svm
X = [[1, 1], [2, 2]]
y = [1, 2]
SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’)
SVRReg.fit(X, y)Resultado
SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto',
kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)Exemplo
Agora, uma vez ajustado, podemos obter o vetor de peso com a ajuda do seguinte script python -
SVRReg.coef_Resultado
array([[0.4, 0.4]])Exemplo
Da mesma forma, podemos obter o valor de outros atributos da seguinte maneira -
SVRReg.predict([[1,1]])Resultado
array([1.1])Da mesma forma, podemos obter os valores de outros atributos também.
NuSVR
NuSVR é Nu Support Vector Regression. É como NuSVC, mas NuSVR usa um parâmetronupara controlar o número de vetores de suporte. E, além disso, ao contrário do NuSVC, ondenu substituiu o parâmetro C, aqui ele substitui epsilon.
Exemplo de Implementação
O seguinte script Python usa sklearn.svm.SVR classe -
from sklearn.svm import NuSVR
import numpy as np
n_samples, n_features = 20, 15
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M
NuSVRReg.fit(X, y)Resultado
NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto',
kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001,
verbose = False)Exemplo
Agora, uma vez ajustado, podemos obter o vetor de peso com a ajuda do seguinte script python -
NuSVRReg.coef_Resultado
array(
[
[-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
-0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
]
)Da mesma forma, podemos obter o valor de outros atributos também.
LinearSVR
É a regressão do vetor de suporte linear. É semelhante ao SVR com kernel = 'linear'. A diferença entre eles é queLinearSVR implementado em termos de liblinear, enquanto SVC implementado em libsvm. Essa é a razãoLinearSVRtem mais flexibilidade na escolha de penalidades e funções de perda. Também é melhor dimensionado para um grande número de amostras.
Se falarmos sobre seus parâmetros e atributos, então ele não suporta ‘kernel’ porque é considerado linear e também carece de alguns dos atributos como support_, support_vectors_, n_support_, fit_status_ e, dual_coef_.
No entanto, ele suporta parâmetros de 'perda' da seguinte forma -
loss - string, opcional, padrão = 'epsilon_insensitive'
Ele representa a função de perda em que a perda insensível a epsilon é a perda L1 e a perda insensível a epsilon quadrada é a perda L2.
Exemplo de Implementação
O seguinte script Python usa sklearn.svm.LinearSVR classe -
from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 4, random_state = 0)
LSVRReg = LinearSVR(dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive',tol = 1e-5)
LSVRReg.fit(X, y)Resultado
LinearSVR(
C=1.0, dual=False, epsilon=0.0, fit_intercept=True,
intercept_scaling=1.0, loss='squared_epsilon_insensitive',
max_iter=1000, random_state=0, tol=1e-05, verbose=0
)Exemplo
Agora, uma vez ajustado, o modelo pode prever novos valores da seguinte forma -
LSRReg.predict([[0,0,0,0]])Resultado
array([-0.01041416])Exemplo
Para o exemplo acima, podemos obter o vetor de peso com a ajuda do seguinte script python -
LSRReg.coef_Resultado
array([20.47354746, 34.08619401, 67.23189022, 87.47017787])Exemplo
Da mesma forma, podemos obter o valor de interceptar com a ajuda do seguinte script python -
LSRReg.intercept_Resultado
array([-0.01041416])Aqui, aprenderemos sobre o que é detecção de anomalias no Sklearn e como ela é usada na identificação dos pontos de dados.
A detecção de anomalias é uma técnica usada para identificar pontos de dados no conjunto de dados que não se ajustam bem ao restante dos dados. Ele tem muitas aplicações nos negócios, como detecção de fraude, detecção de intrusão, monitoramento da integridade do sistema, vigilância e manutenção preditiva. As anomalias, também chamadas de outlier, podem ser divididas nas seguintes três categorias -
Point anomalies - Ocorre quando uma instância de dados individual é considerada anômala em relação ao restante dos dados.
Contextual anomalies- Esse tipo de anomalia é específico do contexto. Ocorre se uma instância de dados for anômala em um contexto específico.
Collective anomalies - Ocorre quando uma coleção de instâncias de dados relacionadas é anômala em relação ao conjunto de dados inteiro em vez de valores individuais.
Métodos
Dois métodos a saber outlier detection e novelty detectionpode ser usado para detecção de anomalias. É necessário ver a distinção entre eles.
Detecção de outlier
Os dados de treinamento contêm outliers que estão longe do resto dos dados. Esses outliers são definidos como observações. Essa é a razão, os estimadores de detecção de outliers sempre tentam ajustar a região com dados de treinamento mais concentrados, ignorando as observações desviantes. Também é conhecido como detecção de anomalia não supervisionada.
Detecção de novidade
Ele se preocupa com a detecção de um padrão não observado em novas observações que não está incluído nos dados de treinamento. Aqui, os dados de treinamento não são poluídos pelos outliers. Também é conhecido como detecção de anomalia semissupervisionada.
Há um conjunto de ferramentas de ML, fornecidas pelo scikit-learn, que podem ser usadas tanto para detecção de outliers quanto para detecção de novidades. Essas ferramentas primeiro implementam a aprendizagem de objetos a partir dos dados de forma não supervisionada, usando o método fit () da seguinte forma -
estimator.fit(X_train)Agora, as novas observações seriam classificadas como inliers (labeled 1) ou outliers (labeled -1) usando o método predict () da seguinte maneira -
estimator.fit(X_test)O estimador calculará primeiro a função de pontuação bruta e, em seguida, o método de previsão fará uso do limite nessa função de pontuação bruta. Podemos acessar esta função de pontuação bruta com a ajuda descore_sample método e pode controlar o limite por contamination parâmetro.
Nós também podemos definir decision_function método que define outliers como valor negativo e inliers como valor não negativo.
estimator.decision_function(X_test)Algoritmos Sklearn para detecção de outlier
Vamos começar entendendo o que é um envelope elíptico.
Ajustando um envelope elíptico
Este algoritmo assume que os dados regulares vêm de uma distribuição conhecida, como a distribuição Gaussiana. Para detecção de outliers, o Scikit-learn fornece um objeto chamadocovariance.EllipticEnvelop.
Este objeto ajusta uma estimativa de covariância robusta aos dados e, portanto, ajusta uma elipse aos pontos de dados centrais. Ele ignora os pontos fora do modo central.
Parâmetros
A tabela a seguir consiste nos parâmetros usados por sklearn. covariance.EllipticEnvelop método -
| Sr. Não | Parâmetro e Descrição |
|---|---|
| 1 | store_precision - Booleano, opcional, padrão = Verdadeiro Podemos especificá-lo se a precisão estimada for armazenada. |
| 2 | assume_centered - Booleano, opcional, padrão = False Se definirmos como False, ele calculará a localização robusta e a covariância diretamente com a ajuda do algoritmo FastMCD. Por outro lado, se definido como True, ele irá computar o suporte de localização robusta e covariana. |
| 3 | support_fraction - flutuar em (0., 1.), opcional, padrão = Nenhum Este parâmetro informa ao método a proporção de pontos a serem incluídos no suporte das estimativas de MCD brutas. |
| 4 | contamination - flutuar em (0., 1.), opcional, padrão = 0,1 Ele fornece a proporção de outliers no conjunto de dados. |
| 5 | random_state - int, instância RandomState ou Nenhum, opcional, padrão = nenhum Este parâmetro representa a semente do número pseudoaleatório gerado que é usado ao embaralhar os dados. A seguir estão as opções -
|
Atributos
A tabela a seguir consiste nos atributos usados por sklearn. covariance.EllipticEnvelop método -
| Sr. Não | Atributos e descrição |
|---|---|
| 1 | support_ - tipo matriz, forma (n_samples,) Ele representa a máscara das observações usadas para calcular estimativas robustas de localização e forma. |
| 2 | location_ - tipo matriz, forma (n_features) Ele retorna a localização robusta estimada. |
| 3 | covariance_ - tipo array, forma (n_features, n_features) Ele retorna a matriz de covariância robusta estimada. |
| 4 | precision_ - tipo array, forma (n_features, n_features) Ele retorna a matriz pseudo inversa estimada. |
| 5 | offset_ - flutuar É usado para definir a função de decisão a partir das pontuações brutas. decision_function = score_samples -offset_ |
Implementation Example
import numpy as np^M
from sklearn.covariance import EllipticEnvelope^M
true_cov = np.array([[.5, .6],[.6, .4]])
X = np.random.RandomState(0).multivariate_normal(mean = [0, 0], cov=true_cov,size=500)
cov = EllipticEnvelope(random_state = 0).fit(X)^M
# Now we can use predict method. It will return 1 for an inlier and -1 for an outlier.
cov.predict([[0, 0],[2, 2]])Output
array([ 1, -1])Floresta de Isolamento
No caso de um conjunto de dados de alta dimensão, uma maneira eficiente de detecção de valores discrepantes é usar florestas aleatórias. O scikit-learn forneceensemble.IsolationForestmétodo que isola as observações ao selecionar aleatoriamente uma característica. Em seguida, ele seleciona aleatoriamente um valor entre os valores máximo e mínimo dos recursos selecionados.
Aqui, o número de divisões necessárias para isolar uma amostra é equivalente ao comprimento do caminho do nó raiz ao nó final.
Parâmetros
A tabela a seguir consiste nos parâmetros usados por sklearn. ensemble.IsolationForest método -
| Sr. Não | Parâmetro e Descrição |
|---|---|
| 1 | n_estimators - int, opcional, padrão = 100 Ele representa o número de estimadores de base no conjunto. |
| 2 | max_samples - int ou float, opcional, padrão = “auto” Ele representa o número de amostras a serem retiradas de X para treinar cada estimador de base. Se escolhermos int como seu valor, ele extrairá amostras de max_samples. Se escolhermos float como seu valor, ele desenhará max_samples ∗ .shape [0] samples. E, se escolhermos auto como seu valor, ele desenhará max_samples = min (256, n_samples). |
| 3 | support_fraction - flutuar em (0., 1.), opcional, padrão = Nenhum Este parâmetro informa ao método a proporção de pontos a serem incluídos no suporte das estimativas de MCD brutas. |
| 4 | contamination - automático ou flutuante, opcional, padrão = automático Ele fornece a proporção de outliers no conjunto de dados. Se definirmos como padrão, ou seja, automático, ele determinará o limite como no papel original. Se definido como flutuante, a faixa de contaminação estará na faixa de [0,0.5]. |
| 5 | random_state - int, instância RandomState ou Nenhum, opcional, padrão = nenhum Este parâmetro representa a semente do número pseudoaleatório gerado que é usado ao embaralhar os dados. A seguir estão as opções -
|
| 6 | max_features - int ou float, opcional (padrão = 1.0) Ele representa o número de recursos a serem extraídos de X para treinar cada estimador de base. Se escolhermos int como seu valor, ele desenhará os recursos max_features. Se escolhermos float como seu valor, ele desenhará amostras max_features * X.shape []. |
| 7 | bootstrap - Booleano, opcional (padrão = Falso) Sua opção padrão é False, o que significa que a amostragem seria realizada sem substituição. E por outro lado, se definido como True, significa que as árvores individuais são ajustadas em um subconjunto aleatório dos dados de treinamento amostrados com substituição. |
| 8 | n_jobs - int ou nenhum, opcional (padrão = nenhum) Ele representa o número de trabalhos a serem executados em paralelo para fit() e predict() métodos ambos. |
| 9 | verbose - int, opcional (padrão = 0) Este parâmetro controla o detalhamento do processo de construção da árvore. |
| 10 | warm_start - Bool, opcional (padrão = False) Se warm_start = true, podemos reutilizar a solução de chamadas anteriores para ajustar e adicionar mais estimadores ao conjunto. Mas se for definido como falso, precisamos ajustar uma floresta totalmente nova. |
Atributos
A tabela a seguir consiste nos atributos usados por sklearn. ensemble.IsolationForest método -
| Sr. Não | Atributos e descrição |
|---|---|
| 1 | estimators_ - lista de DecisionTreeClassifier Fornecendo a coleção de todos os subestimadores ajustados. |
| 2 | max_samples_ - inteiro Ele fornece o número real de amostras usadas. |
| 3 | offset_ - flutuar É usado para definir a função de decisão a partir das pontuações brutas. decision_function = score_samples -offset_ |
Implementation Example
O script Python abaixo usará sklearn. ensemble.IsolationForest método para ajustar 10 árvores em dados fornecidos
from sklearn.ensemble import IsolationForest
import numpy as np
X = np.array([[-1, -2], [-3, -3], [-3, -4], [0, 0], [-50, 60]])
OUTDClf = IsolationForest(n_estimators = 10)
OUTDclf.fit(X)Output
IsolationForest(
behaviour = 'old', bootstrap = False, contamination='legacy',
max_features = 1.0, max_samples = 'auto', n_estimators = 10, n_jobs=None,
random_state = None, verbose = 0
)Fator Outlier Local
O algoritmo Local Outlier Factor (LOF) é outro algoritmo eficiente para realizar detecção de valores discrepantes em dados de alta dimensão. O scikit-learn forneceneighbors.LocalOutlierFactormétodo que calcula uma pontuação, denominado fator de outlier local, refletindo o grau de anomalia das observações. A lógica principal desse algoritmo é detectar as amostras que possuem uma densidade substancialmente menor que suas vizinhas. É por isso que ele mede o desvio de densidade local de determinados pontos de dados em relação a seus vizinhos.
Parâmetros
A tabela a seguir consiste nos parâmetros usados por sklearn. neighbors.LocalOutlierFactor método
| Sr. Não | Parâmetro e Descrição |
|---|---|
| 1 | n_neighbors - int, opcional, padrão = 20 Ele representa o número de vizinhos usados por padrão para a consulta de vizinhos. Todas as amostras seriam usadas se. |
| 2 | algorithm - opcional Qual algoritmo a ser usado para calcular os vizinhos mais próximos.
|
| 3 | leaf_size - int, opcional, padrão = 30 O valor deste parâmetro pode afetar a velocidade de construção e consulta. Também afeta a memória necessária para armazenar a árvore. Este parâmetro é passado para algoritmos BallTree ou KdTree. |
| 4 | contamination - automático ou flutuante, opcional, padrão = automático Ele fornece a proporção de outliers no conjunto de dados. Se definirmos como padrão, ou seja, automático, ele determinará o limite como no papel original. Se definido como flutuante, a faixa de contaminação estará na faixa de [0,0.5]. |
| 5 | metric - string ou chamável, padrão Ele representa a métrica usada para cálculo de distância. |
| 6 | P - int, opcional (padrão = 2) É o parâmetro para a métrica de Minkowski. P = 1 é equivalente a usar distância_de_manhattan, ou seja, L1, enquanto P = 2 é equivalente a usar distância_euclidiana, ou seja, L2. |
| 7 | novelty - Booleano, (padrão = Falso) Por padrão, o algoritmo LOF é usado para detecção de outlier, mas pode ser usado para detecção de novidade se definirmos novidade = verdadeiro. |
| 8 | n_jobs - int ou nenhum, opcional (padrão = nenhum) Ele representa o número de trabalhos a serem executados em paralelo para os métodos fit () e Predict (). |
Atributos
A tabela a seguir consiste nos atributos usados por sklearn.neighbors.LocalOutlierFactor método -
| Sr. Não | Atributos e descrição |
|---|---|
| 1 | negative_outlier_factor_ - matriz numpy, forma (n_samples,) Fornecendo LOF oposto dos exemplos de treinamento. |
| 2 | n_neighbors_ - inteiro Ele fornece o número real de vizinhos usados para consultas de vizinhos. |
| 3 | offset_ - flutuar É usado para definir os rótulos binários das pontuações brutas. |
Implementation Example
O script Python fornecido abaixo usará sklearn.neighbors.LocalOutlierFactor método para construir a classe NeighboursClassifier a partir de qualquer array correspondente ao nosso conjunto de dados
from sklearn.neighbors import NearestNeighbors
samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]
LOFneigh = NearestNeighbors(n_neighbors = 1, algorithm = "ball_tree",p=1)
LOFneigh.fit(samples)Output
NearestNeighbors(
algorithm = 'ball_tree', leaf_size = 30, metric='minkowski',
metric_params = None, n_jobs = None, n_neighbors = 1, p = 1, radius = 1.0
)Example
Agora, podemos perguntar a partir desse classificador construído se é o ponto mais próximo a [0,5, 1., 1,5] usando o seguinte script python -
print(neigh.kneighbors([[.5, 1., 1.5]])Output
(array([[1.7]]), array([[1]], dtype = int64))SVM de uma classe
O SVM de uma classe, introduzido por Schölkopf et al., É a detecção de outlier não supervisionada. Também é muito eficiente em dados de alta dimensão e estima o suporte de uma distribuição de alta dimensão. É implementado noSupport Vector Machines módulo no Sklearn.svm.OneClassSVMobjeto. Para definir uma fronteira, ele requer um kernel (mais usado é o RBF) e um parâmetro escalar.
Para melhor compreensão, vamos ajustar nossos dados com svm.OneClassSVM objeto -
Exemplo
from sklearn.svm import OneClassSVM
X = [[0], [0.89], [0.90], [0.91], [1]]
OSVMclf = OneClassSVM(gamma = 'scale').fit(X)Agora, podemos obter o score_samples para os dados de entrada da seguinte forma -
OSVMclf.score_samples(X)Resultado
array([1.12218594, 1.58645126, 1.58673086, 1.58645127, 1.55713767])Este capítulo o ajudará a entender os métodos do vizinho mais próximo no Sklearn.
O método de aprendizagem baseado em vizinho é de ambos os tipos, a saber supervised e unsupervised. O aprendizado supervisionado baseado em vizinhos pode ser usado tanto para classificação quanto para problemas preditivos de regressão, mas é usado principalmente para problemas preditivos de classificação na indústria.
Os métodos de aprendizagem baseados em vizinhos não possuem uma fase de treinamento especializada e usam todos os dados para treinamento durante a classificação. Ele também não assume nada sobre os dados subjacentes. Essa é a razão pela qual eles são preguiçosos e não paramétricos por natureza.
O principal princípio por trás dos métodos de vizinho mais próximo é -
Para encontrar um número predefinido de armário de amostras de treinamento em distância para o novo ponto de dados
Preveja o rótulo a partir desse número de amostras de treinamento.
Aqui, o número de amostras pode ser uma constante definida pelo usuário, como no aprendizado de K-vizinho mais próximo ou variar com base na densidade local do ponto, como no aprendizado de vizinho baseado em raio.
Módulo sklearn.neighbors
Scikit-learn tem sklearn.neighborsmódulo que fornece funcionalidade para métodos de aprendizagem baseados em vizinhos não supervisionados e supervisionados. Como entrada, as classes neste módulo podem lidar com matrizes NumPy ouscipy.sparse matrizes.
Tipos de algoritmos
Diferentes tipos de algoritmos que podem ser usados na implementação de métodos baseados em vizinhos são os seguintes -
Força bruta
O cálculo da força bruta das distâncias entre todos os pares de pontos no conjunto de dados fornece a implementação de pesquisa de vizinho mais ingênua. Matematicamente, para N amostras em dimensões D, escalas de abordagem de força bruta como0[DN2]
Para pequenas amostras de dados, esse algoritmo pode ser muito útil, mas se torna inviável à medida que o número de amostras aumenta. A pesquisa de vizinhança de força bruta pode ser ativada escrevendo a palavra-chavealgorithm=’brute’.
Árvore KD
Uma das estruturas de dados baseadas em árvore que foram inventadas para lidar com as ineficiências computacionais da abordagem de força bruta é a estrutura de dados em árvore KD. Basicamente, a árvore KD é uma estrutura de árvore binária que é chamada de árvore K-dimensional. Ele particiona recursivamente o espaço de parâmetros ao longo dos eixos de dados, dividindo-o em regiões ortográficas aninhadas nas quais os pontos de dados são preenchidos.
Vantagens
A seguir estão algumas vantagens do algoritmo de árvore KD -
Construction is fast - Como o particionamento é realizado apenas ao longo dos eixos de dados, a construção da árvore KD é muito rápida.
Less distance computations- Este algoritmo leva muito menos cálculos de distância para determinar o vizinho mais próximo de um ponto de consulta. É preciso apenas[ ()] cálculos de distância.
Desvantagens
Fast for only low-dimensional neighbor searches- É muito rápido para buscas vizinhas de baixa dimensão (D <20), mas à medida que D aumenta, torna-se ineficiente. Como o particionamento é realizado apenas ao longo dos eixos de dados,
As pesquisas de vizinho da árvore KD podem ser habilitadas escrevendo a palavra-chave algorithm=’kd_tree’.
Ball Tree
Como sabemos que a árvore KD é ineficiente em dimensões superiores, portanto, para resolver essa ineficiência da árvore KD, a estrutura de dados da árvore Ball foi desenvolvida. Matematicamente, divide os dados de forma recursiva, em nós definidos por um centróide C e raio r, de modo que cada ponto do nó fique dentro da hiperesfera definida pelo centróideC e raio r. Ele usa a desigualdade triangular, fornecida abaixo, o que reduz o número de pontos candidatos para uma pesquisa de vizinho
$$\arrowvert X+Y\arrowvert\leq \arrowvert X\arrowvert+\arrowvert Y\arrowvert$$Vantagens
A seguir estão algumas vantagens do algoritmo Ball Tree -
Efficient on highly structured data - Como a árvore de bolas particiona os dados em uma série de hiperesferas de aninhamento, é eficiente em dados altamente estruturados.
Out-performs KD-tree - Ball tree supera a árvore KD em grandes dimensões porque tem geometria esférica dos nós da árvore ball.
Desvantagens
Costly - Particionar os dados em uma série de hiperesferas de aninhamento torna sua construção muito cara.
As pesquisas de vizinho da árvore de bolas podem ser habilitadas escrevendo a palavra-chave algorithm=’ball_tree’.
Algoritmo de escolha de vizinhos mais próximos
A escolha de um algoritmo ideal para um determinado conjunto de dados depende dos seguintes fatores -
Número de amostras (N) e Dimensionalidade (D)
Esses são os fatores mais importantes a serem considerados ao escolher o algoritmo do vizinho mais próximo. É por causa das razões apresentadas abaixo -
O tempo de consulta do algoritmo de Força Bruta cresce como O [DN].
O tempo de consulta do algoritmo Ball tree cresce como O [D log (N)].
O tempo de consulta do algoritmo da árvore KD muda com D de uma maneira estranha que é muito difícil de caracterizar. Quando D <20, o custo é O [D log (N)] e este algoritmo é muito eficiente. Por outro lado, é ineficiente no caso quando D> 20 porque o custo aumenta para quase O [DN].
Estrutura de dados
Outro fator que afeta o desempenho desses algoritmos é a dimensionalidade intrínseca dos dados ou a dispersão dos dados. É porque os tempos de consulta dos algoritmos da árvore Ball e da árvore KD podem ser muito influenciados por ele. Considerando que o tempo de consulta do algoritmo de Força Bruta não é alterado pela estrutura de dados. Geralmente, os algoritmos Ball tree e KD tree produzem um tempo de consulta mais rápido quando implantados em dados mais esparsos com menor dimensionalidade intrínseca.
Número de vizinhos (k)
O número de vizinhos (k) solicitados para um ponto de consulta afeta o tempo de consulta dos algoritmos da árvore Ball e da árvore KD. O tempo de consulta torna-se mais lento conforme o número de vizinhos (k) aumenta. Considerando que o tempo de consulta da Força Bruta permanecerá inalterado pelo valor de k.
Número de pontos de consulta
Como eles precisam da fase de construção, os algoritmos da árvore KD e da árvore Ball serão eficazes se houver um grande número de pontos de consulta. Por outro lado, se houver um número menor de pontos de consulta, o algoritmo Brute Force tem um desempenho melhor do que os algoritmos de árvore KD e Ball tree.
k-NN (k-vizinho mais próximo), um dos algoritmos de aprendizado de máquina mais simples, é não paramétrico e preguiçoso por natureza. Não paramétrico significa que não há suposição para a distribuição de dados subjacente, ou seja, a estrutura do modelo é determinada a partir do conjunto de dados. Aprendizagem lenta ou baseada em instância significa que, para fins de geração de modelo, não requer nenhum ponto de dados de treinamento e todos os dados de treinamento são usados na fase de teste.
O algoritmo k-NN consiste nas duas etapas a seguir -
Passo 1
Nesta etapa, ele calcula e armazena os k vizinhos mais próximos para cada amostra no conjunto de treinamento.
Passo 2
Nesta etapa, para uma amostra não rotulada, ele recupera os k vizinhos mais próximos do conjunto de dados. Então, entre esses k-vizinhos mais próximos, ele prevê a classe por meio da votação (a classe com maioria de votos vence).
O módulo, sklearn.neighbors que implementa o algoritmo de vizinhos k-mais próximos, fornece a funcionalidade para unsupervised assim como supervised métodos de aprendizagem baseados em vizinhos.
Os vizinhos mais próximos não supervisionados implementam algoritmos diferentes (BallTree, KDTree ou Brute Force) para encontrar o (s) vizinho (s) mais próximo (s) para cada amostra. Esta versão não supervisionada é basicamente apenas o passo 1, que é discutido acima, e a base de muitos algoritmos (KNN e K-means sendo o famoso) que requerem a busca de vizinho. Em palavras simples, é o aluno não supervisionado para a implementação de pesquisas de vizinhos.
Por outro lado, a aprendizagem supervisionada baseada em vizinhos é usada tanto para classificação quanto para regressão.
Aprendizagem KNN Não Supervisionada
Conforme discutido, existem muitos algoritmos como KNN e K-Means que requerem pesquisas de vizinho mais próximo. É por isso que o Scikit-learn decidiu implementar a parte de pesquisa de vizinhos como seu próprio “aprendiz”. A razão por trás de fazer a pesquisa de vizinho como um aluno separado é que calcular todas as distâncias entre pares para encontrar um vizinho mais próximo obviamente não é muito eficiente. Vamos ver o módulo usado pelo Sklearn para implementar o aprendizado do vizinho mais próximo não supervisionado junto com o exemplo.
Módulo Scikit-learn
sklearn.neighbors.NearestNeighborsé o módulo usado para implementar o aprendizado do vizinho mais próximo não supervisionado. Ele usa algoritmos de vizinho mais próximo específicos chamados BallTree, KDTree ou Brute Force. Em outras palavras, ele atua como uma interface uniforme para esses três algoritmos.
Parâmetros
A tabela a seguir consiste nos parâmetros usados por NearestNeighbors módulo -
| Sr. Não | Parâmetro e Descrição |
|---|---|
| 1 | n_neighbors - int, opcional O número de vizinhos a serem obtidos. O valor padrão é 5. |
| 2 | radius - float, opcional Limita a distância dos vizinhos aos retornos. O valor padrão é 1.0. |
| 3 | algorithm - {'auto', 'ball_tree', 'kd_tree', 'brute'}, opcional Este parâmetro pegará o algoritmo (BallTree, KDTree ou Brute-force) que você deseja usar para calcular os vizinhos mais próximos. Se você fornecer 'auto', ele tentará decidir o algoritmo mais apropriado com base nos valores passados para o método de ajuste. |
| 4 | leaf_size - int, opcional Isso pode afetar a velocidade da construção e da consulta, bem como a memória necessária para armazenar a árvore. É passado para BallTree ou KDTree. Embora o valor ideal dependa da natureza do problema, seu valor padrão é 30. |
| 5 | metric - string ou chamável É a métrica a ser usada para cálculo de distância entre pontos. Podemos passá-lo como uma string ou função que pode ser chamada. No caso de função chamável, a métrica é chamada em cada par de linhas e o valor resultante é registrado. É menos eficiente do que passar o nome da métrica como uma string. Podemos escolher a métrica de scikit-learn ou scipy.spatial.distance. os valores válidos são os seguintes - Scikit-learn - ['cosine', 'manhattan', 'Euclidean', 'l1', 'l2', 'cityblock'] Scipy.spatial.distance - ['braycurtis', 'canberra', 'chebyshev', 'dice', 'hamming', 'jaccard', 'correlação', 'kulsinski', 'mahalanobis', 'minkowski', 'rogerstanimoto', 'russellrao', ' sokalmicheme ',' sokalsneath ',' seuclidean ',' sqeuclidean ',' yule ']. A métrica padrão é 'Minkowski'. |
| 6 | P - inteiro, opcional É o parâmetro para a métrica de Minkowski. O valor padrão é 2, que é equivalente a usar distância_euclidiana (l2). |
| 7 | metric_params - dict, opcional Estes são os argumentos de palavra-chave adicionais para a função métrica. O valor padrão é nenhum. |
| 8 | N_jobs - int ou nenhum, opcional Ele redefine o número de trabalhos paralelos a serem executados para pesquisa de vizinho. O valor padrão é nenhum. |
Implementation Example
O exemplo abaixo encontrará os vizinhos mais próximos entre dois conjuntos de dados usando o sklearn.neighbors.NearestNeighbors módulo.
Primeiro, precisamos importar o módulo e os pacotes necessários -
from sklearn.neighbors import NearestNeighbors
import numpy as npAgora, depois de importar os pacotes, defina os conjuntos de dados entre os quais queremos encontrar os vizinhos mais próximos -
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])Em seguida, aplique o algoritmo de aprendizado não supervisionado, como segue -
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm = 'ball_tree')Em seguida, ajuste o modelo com o conjunto de dados de entrada.
nrst_neigh.fit(Input_data)Agora, encontre os K-vizinhos do conjunto de dados. Ele retornará os índices e distâncias dos vizinhos de cada ponto.
distances, indices = nbrs.kneighbors(Input_data)
indicesOutput
array(
[
[0, 1, 3],
[1, 2, 0],
[2, 1, 0],
[3, 4, 0],
[4, 5, 3],
[5, 6, 4],
[6, 5, 4]
], dtype = int64
)
distancesOutput
array(
[
[0. , 1.41421356, 2.23606798],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 2.82842712],
[0. , 1.41421356, 2.23606798],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 2.82842712]
]
)A saída acima mostra que o vizinho mais próximo de cada ponto é o próprio ponto, ou seja, em zero. É porque o conjunto de consultas corresponde ao conjunto de treinamento.
Example
Também podemos mostrar uma conexão entre pontos vizinhos, produzindo um gráfico esparso como segue -
nrst_neigh.kneighbors_graph(Input_data).toarray()Output
array(
[
[1., 1., 0., 1., 0., 0., 0.],
[1., 1., 1., 0., 0., 0., 0.],
[1., 1., 1., 0., 0., 0., 0.],
[1., 0., 0., 1., 1., 0., 0.],
[0., 0., 0., 1., 1., 1., 0.],
[0., 0., 0., 0., 1., 1., 1.],
[0., 0., 0., 0., 1., 1., 1.]
]
)Uma vez que ajustamos o não supervisionado NearestNeighbors modelo, os dados serão armazenados em uma estrutura de dados com base no valor definido para o argumento ‘algorithm’. Depois disso, podemos usar este aluno não supervisionadokneighbors em um modelo que requer pesquisas vizinhas.
Complete working/executable program
from sklearn.neighbors import NearestNeighbors
import numpy as np
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm='ball_tree')
nrst_neigh.fit(Input_data)
distances, indices = nbrs.kneighbors(Input_data)
indices
distances
nrst_neigh.kneighbors_graph(Input_data).toarray()Aprendizagem KNN Supervisionada
A aprendizagem supervisionada baseada em vizinhos é usada para seguir -
- Classificação, para os dados com rótulos discretos
- Regressão, para os dados com rótulos contínuos.
Classificador de Vizinho Mais Próximo
Podemos entender a classificação baseada em vizinhos com a ajuda das seguintes duas características -
- É calculado a partir de uma votação por maioria simples dos vizinhos mais próximos de cada ponto.
- Ele simplesmente armazena instâncias dos dados de treinamento, por isso é um tipo de aprendizado não generalizante.
Módulos de aprendizagem Scikit
A seguir estão os dois tipos diferentes de classificadores de vizinho mais próximo usados pelo scikit-learn -
| S.No. | Classificadores e descrição |
|---|---|
| 1 | KNeighboursClassifier O K no nome deste classificador representa os k vizinhos mais próximos, onde k é um valor inteiro especificado pelo usuário. Portanto, como o nome sugere, esse classificador implementa o aprendizado com base nos k vizinhos mais próximos. A escolha do valor de k depende dos dados. |
| 2 | RadiusNeighborsClassifier O Raio no nome deste classificador representa os vizinhos mais próximos dentro de um raio especificado r, onde r é um valor de ponto flutuante especificado pelo usuário. Portanto, como o nome sugere, esse classificador implementa o aprendizado com base no número de vizinhos dentro de um raio fixo r de cada ponto de treinamento. |
Regressor vizinho mais próximo
É usado nos casos em que os rótulos de dados são de natureza contínua. Os rótulos de dados atribuídos são calculados com base na média dos rótulos de seus vizinhos mais próximos.
A seguir estão os dois tipos diferentes de regressores do vizinho mais próximo usados pelo scikit-learn -
KNeighboursRegressor
O K no nome deste regressor representa os k vizinhos mais próximos, onde k é um integer valueespecificado pelo usuário. Portanto, como o nome sugere, esse regressor implementa o aprendizado com base nos k vizinhos mais próximos. A escolha do valor de k depende dos dados. Vamos entender melhor com a ajuda de um exemplo de implementação.
A seguir estão os dois tipos diferentes de regressores do vizinho mais próximo usados pelo scikit-learn -
Exemplo de Implementação
Neste exemplo, iremos implementar KNN no conjunto de dados denominado Conjunto de dados Iris Flower usando o scikit-learn KNeighborsRegressor.
Primeiro, importe o conjunto de dados da íris da seguinte forma -
from sklearn.datasets import load_iris
iris = load_iris()Agora, precisamos dividir os dados em dados de treinamento e teste. Estaremos usando Sklearntrain_test_split função para dividir os dados na proporção de 70 (dados de treinamento) e 20 (dados de teste) -
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)Em seguida, faremos o escalonamento de dados com a ajuda do módulo de pré-processamento Sklearn da seguinte maneira -
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)Em seguida, importe o KNeighborsRegressor classe de Sklearn e fornecer o valor de vizinhos como segue.
Exemplo
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 8)
knnr.fit(X_train, y_train)Resultado
KNeighborsRegressor(
algorithm = 'auto', leaf_size = 30, metric = 'minkowski',
metric_params = None, n_jobs = None, n_neighbors = 8, p = 2,
weights = 'uniform'
)Exemplo
Agora, podemos encontrar o MSE (erro quadrático médio) da seguinte forma -
print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))Resultado
The MSE is: 4.4333349609375Exemplo
Agora, use-o para prever o valor da seguinte maneira -
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))Resultado
[0.66666667]Programa completo de trabalho / executável
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=8)
knnr.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))RadiusNeighborsRegressor
O raio no nome deste regressor representa os vizinhos mais próximos dentro de um raio especificado r, onde r é um valor de ponto flutuante especificado pelo usuário. Conseqüentemente, como o nome sugere, este regressor implementa o aprendizado com base no número de vizinhos dentro de um raio fixo r de cada ponto de treinamento. Vamos entender melhor com a ajuda de um exemplo de implementação -
Exemplo de Implementação
Neste exemplo, iremos implementar KNN no conjunto de dados denominado Conjunto de dados Iris Flower usando o scikit-learn RadiusNeighborsRegressor -
Primeiro, importe o conjunto de dados da íris da seguinte forma -
from sklearn.datasets import load_iris
iris = load_iris()Agora, precisamos dividir os dados em dados de treinamento e teste. Estaremos usando a função sklearn train_test_split para dividir os dados na proporção de 70 (dados de treinamento) e 20 (dados de teste) -
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)Em seguida, faremos o escalonamento de dados com a ajuda do módulo de pré-processamento Sklearn da seguinte maneira -
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)Em seguida, importe o RadiusneighborsRegressor classe do Sklearn e forneça o valor de radius da seguinte forma -
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X_train, y_train)Exemplo
Agora, podemos encontrar o MSE (erro quadrático médio) da seguinte forma -
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))Resultado
The MSE is: The MSE is: 5.666666666666667Exemplo
Agora, use-o para prever o valor da seguinte maneira -
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))Resultado
[1.]Programa completo de trabalho / executável
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))Os métodos Naïve Bayes são um conjunto de algoritmos de aprendizagem supervisionada baseados na aplicação do teorema de Bayes com uma forte suposição de que todos os preditores são independentes entre si, ou seja, a presença de uma característica em uma classe é independente da presença de qualquer outra característica na mesma classe. Esta é uma suposição ingênua que é o motivo pelo qual esses métodos são chamados de métodos Naïve Bayes.
O teorema de Bayes estabelece a seguinte relação a fim de encontrar a probabilidade posterior de classe, ou seja, a probabilidade de um rótulo e algumas características observadas, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$.
$$P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)=\left(\frac{P\lgroup Y\rgroup P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)}{P\left(\begin{array}{c} features\end{array}\right)}\right)$$Aqui, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$ é a probabilidade posterior da classe.
$P\left(\begin{array}{c} Y\end{array}\right)$ é a probabilidade anterior da classe.
$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ é a probabilidade que é a probabilidade do preditor de determinada classe.
$P\left(\begin{array}{c} features\end{array}\right)$ é a probabilidade anterior do preditor.
O Scikit-learn fornece diferentes modelos de classificadores Bayes ingênuos, a saber, Gaussiano, Multinomial, Complemento e Bernoulli. Todos eles diferem principalmente pela suposição que fazem sobre a distribuição de$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ ou seja, a probabilidade de preditor dada classe.
| Sr. Não | Modelo e descrição |
|---|---|
| 1 | Gaussian Naïve Bayes O classificador Gaussian Naïve Bayes assume que os dados de cada rótulo são extraídos de uma distribuição Gaussiana simples. |
| 2 | Multinomial Naïve Bayes Ele assume que os recursos são extraídos de uma distribuição Multinomial simples. |
| 3 | Bernoulli Naïve Bayes A suposição neste modelo é que os recursos são binários (0s e 1s) na natureza. Uma aplicação da classificação de Bernoulli Naïve Bayes é a classificação de texto com o modelo de 'saco de palavras' |
| 4 | Complemento Naïve Bayes Ele foi projetado para corrigir as suposições severas feitas pelo classificador Multinomial Bayes. Este tipo de classificador NB é adequado para conjuntos de dados desequilibrados |
Classificador Building Naïve Bayes
Também podemos aplicar o classificador Naïve Bayes no conjunto de dados Scikit-learn. No exemplo abaixo, estamos aplicando GaussianNB e ajustando o conjunto de dados breast_cancer de Scikit-leran.
Exemplo
Import Sklearn
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
data = load_breast_cancer()
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']
print(label_names)
print(labels[0])
print(feature_names[0])
print(features[0])
train, test, train_labels, test_labels = train_test_split(
features,labels,test_size = 0.40, random_state = 42
)
from sklearn.naive_bayes import GaussianNB
GNBclf = GaussianNB()
model = GNBclf.fit(train, train_labels)
preds = GNBclf.predict(test)
print(preds)Resultado
[
1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1
1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1
1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0
1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0
1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1
0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1
1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0
1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1
1 1 1 1 0 1 0 0 1 1 0 1
]A saída acima consiste em uma série de 0s e 1s que são basicamente os valores previstos das classes de tumor, ou seja, maligno e benigno.
Neste capítulo, aprenderemos sobre o método de aprendizagem em Sklearn, que é denominado como árvores de decisão.
As árvores de decisão (DTs) são o método de aprendizagem supervisionado não paramétrico mais poderoso. Eles podem ser usados para as tarefas de classificação e regressão. O principal objetivo dos DTs é criar um modelo que preveja o valor da variável alvo, aprendendo regras de decisão simples deduzidas dos recursos de dados. As árvores de decisão têm duas entidades principais; um é o nó raiz, onde os dados se dividem, e o outro são os nós de decisão ou folhas, onde obtivemos a saída final.
Algoritmos de árvore de decisão
Diferentes algoritmos de árvore de decisão são explicados abaixo -
ID3
Foi desenvolvido por Ross Quinlan em 1986. Também é chamado de Dicotomizador Iterativo 3. O objetivo principal desse algoritmo é encontrar aquelas características categóricas, para cada nó, que produzirão o maior ganho de informação para alvos categóricos.
Ele permite que a árvore cresça até seu tamanho máximo e, em seguida, para melhorar a capacidade da árvore em dados invisíveis, aplica uma etapa de poda. A saída desse algoritmo seria uma árvore de múltiplos caminhos.
C4.5
É o sucessor de ID3 e define dinamicamente um atributo discreto que particiona o valor do atributo contínuo em um conjunto discreto de intervalos. Essa é a razão pela qual removeu a restrição de recursos categóricos. Ele converte a árvore treinada ID3 em conjuntos de regras 'SE-ENTÃO'.
Para determinar a seqüência em que essas regras devem ser aplicadas, a precisão de cada regra será avaliada primeiro.
C5.0
Ele funciona de forma semelhante ao C4.5, mas usa menos memória e cria conjuntos de regras menores. É mais preciso do que C4.5.
CARRINHO
É também denominado Árvores de Classificação e Regressão. Basicamente, ele gera divisões binárias usando os recursos e o limite, gerando o maior ganho de informação em cada nó (chamado de índice de Gini).
A homogeneidade depende do índice de Gini, quanto maior o valor do índice de Gini, maior será a homogeneidade. É como o algoritmo C4.5, mas a diferença é que ele não calcula conjuntos de regras e também não oferece suporte a variáveis de destino numéricas (regressão).
Classificação com árvores de decisão
Nesse caso, as variáveis de decisão são categóricas.
Sklearn Module - A biblioteca Scikit-learn fornece o nome do módulo DecisionTreeClassifier para realizar a classificação multiclasse no conjunto de dados.
Parâmetros
A tabela a seguir consiste nos parâmetros usados por sklearn.tree.DecisionTreeClassifier módulo -
| Sr. Não | Parâmetro e Descrição |
|---|---|
| 1 | criterion - string, padrão opcional = “gini” Ele representa a função de medir a qualidade de uma divisão. Os critérios suportados são “gini” e “entropia”. O padrão é gini, que é para a impureza de Gini, enquanto a entropia é para o ganho de informação. |
| 2 | splitter - string, padrão opcional = “melhor” Ele diz ao modelo qual estratégia da “melhor” ou “aleatória” escolher a divisão em cada nó. |
| 3 | max_depth - int ou nenhum, padrão opcional = nenhum Este parâmetro decide a profundidade máxima da árvore. O valor padrão é Nenhum, o que significa que os nós se expandirão até que todas as folhas sejam puras ou até que todas as folhas contenham menos do que min_smaples_split amostras. |
| 4 | min_samples_split - int, float, padrão opcional = 2 Este parâmetro fornece o número mínimo de amostras necessárias para dividir um nó interno. |
| 5 | min_samples_leaf - int, float, padrão opcional = 1 Este parâmetro fornece o número mínimo de amostras necessárias para estar em um nó folha. |
| 6 | min_weight_fraction_leaf - float, padrão opcional = 0. Com este parâmetro, o modelo obterá a fração mínima ponderada da soma dos pesos necessários para estar em um nó folha. |
| 7 | max_features - int, float, string ou Nenhum, padrão opcional = Nenhum Fornece ao modelo o número de recursos a serem considerados ao procurar a melhor divisão. |
| 8 | random_state - int, instância RandomState ou Nenhum, opcional, padrão = nenhum Este parâmetro representa a semente do número pseudoaleatório gerado que é usado ao embaralhar os dados. A seguir estão as opções -
|
| 9 | max_leaf_nodes - int ou nenhum, padrão opcional = nenhum Este parâmetro permitirá que uma árvore cresça com max_leaf_nodes da melhor maneira possível. O padrão é nenhum, o que significa que haveria um número ilimitado de nós folha. |
| 10 | min_impurity_decrease - float, padrão opcional = 0. Este valor funciona como um critério para um nó se dividir porque o modelo irá dividir um nó se esta divisão induzir uma diminuição da impureza maior ou igual a min_impurity_decrease value. |
| 11 | min_impurity_split - flutuante, padrão = 1e-7 Ele representa o limite para a interrupção precoce do crescimento das árvores. |
| 12 | class_weight - dict, lista de dicts, “balance” ou None, default = None Ele representa os pesos associados às classes. O formulário é {class_label: weight}. Se usarmos a opção padrão, significa que todas as classes devem ter peso um. Por outro lado, se você escolherclass_weight: balanced, ele usará os valores de y para ajustar automaticamente os pesos. |
| 13 | presort - bool, padrão opcional = False Diz ao modelo se deve pré-classificar os dados para acelerar a descoberta das melhores divisões no ajuste. O padrão é falso, mas definido como verdadeiro, pode retardar o processo de treinamento. |
Atributos
A tabela a seguir consiste nos atributos usados por sklearn.tree.DecisionTreeClassifier módulo -
| Sr. Não | Parâmetro e Descrição |
|---|---|
| 1 | feature_importances_ - matriz de forma = [n_features] Este atributo retornará a importância do recurso. |
| 2 | classes_: - array of shape = [n_classes] ou uma lista de tais arrays Ele representa os rótulos das classes, ou seja, o problema de saída única, ou uma lista de matrizes de rótulos de classes, ou seja, o problema de múltiplas saídas. |
| 3 | max_features_ - int Ele representa o valor deduzido do parâmetro max_features. |
| 4 | n_classes_ - int ou lista Ele representa o número de classes, ou seja, o problema de saída única, ou uma lista de número de classes para cada saída, ou seja, problema de múltiplas saídas. |
| 5 | n_features_ - int Dá o número de features quando o método fit () é executado. |
| 6 | n_outputs_ - int Dá o número de outputs quando o método fit () é executado. |
Métodos
A tabela a seguir consiste nos métodos usados por sklearn.tree.DecisionTreeClassifier módulo -
| Sr. Não | Parâmetro e Descrição |
|---|---|
| 1 | apply(self, X [, check_input]) Este método retornará o índice da folha. |
| 2 | decision_path(self, X [, check_input]) Como o nome sugere, este método retornará o caminho de decisão na árvore |
| 3 | fit(self, X, y [, sample_weight, ...]) O método fit () construirá um classificador de árvore de decisão a partir de um determinado conjunto de treinamento (X, y). |
| 4 | get_depth(auto) Como o nome sugere, este método retornará a profundidade da árvore de decisão |
| 5 | get_n_leaves(auto) Como o nome sugere, este método retornará o número de folhas da árvore de decisão. |
| 6 | get_params(auto [, profundo]) Podemos usar este método para obter os parâmetros do estimador. |
| 7 | predict(self, X [, check_input]) Ele irá prever o valor da classe para X. |
| 8 | predict_log_proba(próprio, X) Ele irá prever as probabilidades de log da classe das amostras de entrada fornecidas por nós, X. |
| 9 | predict_proba(self, X [, check_input]) Ele irá prever as probabilidades de classe das amostras de entrada fornecidas por nós, X. |
| 10 | score(self, X, y [, sample_weight]) Como o nome indica, o método score () retornará a precisão média nos dados e rótulos de teste fornecidos. |
| 11 | set_params(self, \ * \ * params) Podemos definir os parâmetros do estimador com este método. |
Exemplo de Implementação
O script Python abaixo usará sklearn.tree.DecisionTreeClassifier módulo para construir um classificador para predizer homem ou mulher a partir de nosso conjunto de dados com 25 amostras e duas características, a saber 'altura' e 'comprimento do cabelo' -
from sklearn import tree
from sklearn.model_selection import train_test_split
X=[[165,19],[175,32],[136,35],[174,65],[141,28],[176,15]
,[131,32],[166,6],[128,32],[179,10],[136,34],[186,2],[12
6,25],[176,28],[112,38],[169,9],[171,36],[116,25],[196,2
5], [196,38], [126,40], [197,20], [150,25], [140,32],[136,35]]
Y=['Man','Woman','Woman','Man','Woman','Man','Woman','Ma
n','Woman','Man','Woman','Man','Woman','Woman','Woman','
Man','Woman','Woman','Man', 'Woman', 'Woman', 'Man', 'Man', 'Woman', 'Woman']
data_feature_names = ['height','length of hair']
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.3, random_state = 1)
DTclf = tree.DecisionTreeClassifier()
DTclf = clf.fit(X,Y)
prediction = DTclf.predict([[135,29]])
print(prediction)Resultado
['Woman']Também podemos prever a probabilidade de cada classe usando o seguinte método python predict_proba () da seguinte maneira -
Exemplo
prediction = DTclf.predict_proba([[135,29]])
print(prediction)Resultado
[[0. 1.]]Regressão com árvores de decisão
Nesse caso, as variáveis de decisão são contínuas.
Sklearn Module - A biblioteca Scikit-learn fornece o nome do módulo DecisionTreeRegressor para aplicar árvores de decisão em problemas de regressão.
Parâmetros
Parâmetros usados por DecisionTreeRegressor são quase iguais aos usados em DecisionTreeClassifiermódulo. A diferença está no parâmetro 'critério'. ParaDecisionTreeRegressor módulos ‘criterion: string, opcional default = “mse” 'parâmetro tem os seguintes valores -
mse- Representa o erro quadrático médio. É igual à redução da variância como critério de seleção de recurso. Ele minimiza a perda L2 usando a média de cada nó terminal.
freidman_mse - Também usa o erro quadrático médio, mas com a pontuação de melhoria de Friedman.
mae- Significa o erro médio absoluto. Ele minimiza a perda de L1 usando a mediana de cada nó terminal.
Outra diferença é que não tem ‘class_weight’ parâmetro.
Atributos
Atributos de DecisionTreeRegressor também são iguais aos de DecisionTreeClassifiermódulo. A diferença é que não tem‘classes_’ e ‘n_classes_' atributos.
Métodos
Métodos de DecisionTreeRegressor também são iguais aos de DecisionTreeClassifiermódulo. A diferença é que não tem‘predict_log_proba()’ e ‘predict_proba()’' atributos.
Exemplo de Implementação
O método fit () no modelo de regressão da árvore de decisão assumirá os valores de ponto flutuante de y. vamos ver um exemplo de implementação simples usandoSklearn.tree.DecisionTreeRegressor -
from sklearn import tree
X = [[1, 1], [5, 5]]
y = [0.1, 1.5]
DTreg = tree.DecisionTreeRegressor()
DTreg = clf.fit(X, y)Uma vez ajustado, podemos usar este modelo de regressão para fazer previsões da seguinte forma -
DTreg.predict([[4, 5]])Resultado
array([1.5])Este capítulo o ajudará a entender as árvores de decisão aleatórias no Sklearn.
Algoritmos de árvore de decisão aleatória
Como sabemos que um DT é geralmente treinado pela divisão recursiva dos dados, mas sendo propenso a overfit, eles foram transformados em florestas aleatórias ao treinar muitas árvores em várias subamostras dos dados. osklearn.ensemble módulo está seguindo dois algoritmos baseados em árvores de decisão aleatórias -
O algoritmo Random Forest
Para cada recurso em consideração, ele calcula a combinação ideal local de recurso / divisão. Na floresta aleatória, cada árvore de decisão do conjunto é construída a partir de uma amostra retirada com substituição do conjunto de treinamento e, em seguida, obtém a previsão de cada uma delas e, por fim, seleciona a melhor solução por meio de votação. Ele pode ser usado tanto para tarefas de classificação como de regressão.
Classificação com floresta aleatória
Para criar um classificador de floresta aleatório, o módulo Scikit-learn fornece sklearn.ensemble.RandomForestClassifier. Ao construir o classificador de floresta aleatório, os principais parâmetros que este módulo usa são‘max_features’ e ‘n_estimators’.
Aqui, ‘max_features’é o tamanho dos subconjuntos aleatórios de recursos a serem considerados ao dividir um nó. Se escolhermos o valor deste parâmetro como nenhum, ele considerará todos os recursos em vez de um subconjunto aleatório. Por outro lado,n_estimatorsé o número de árvores na floresta. Quanto maior o número de árvores, melhor será o resultado. Mas também levará mais tempo para calcular.
Exemplo de implementação
No exemplo a seguir, estamos construindo um classificador de floresta aleatório usando sklearn.ensemble.RandomForestClassifier e também verificando sua precisão usando cross_val_score módulo.
from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers = 100,random_state = 0) RFclf = RandomForestClassifier(n_estimators = 10,max_depth = None,min_samples_split = 2, random_state = 0)
scores = cross_val_score(RFclf, X, y, cv = 5)
scores.mean()Resultado
0.9997Exemplo
Também podemos usar o conjunto de dados sklearn para construir o classificador Random Forest. Como no exemplo a seguir, estamos usando o conjunto de dados da íris. Também encontraremos sua pontuação de precisão e matriz de confusão.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
path = "https://archive.ics.uci.edu/ml/machine-learning-database
s/iris/iris.data"
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
dataset = pd.read_csv(path, names = headernames)
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)
RFclf = RandomForestClassifier(n_estimators = 50)
RFclf.fit(X_train, y_train)
y_pred = RFclf.predict(X_test)
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Resultado
Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 14
Iris-versicolor 1.00 0.95 0.97 19
Iris-virginica 0.92 1.00 0.96 12
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Accuracy: 0.9777777777777777Regressão com Floresta Aleatória
Para criar uma regressão de floresta aleatória, o módulo Scikit-learn fornece sklearn.ensemble.RandomForestRegressor. Ao construir um regressor de floresta aleatório, ele usará os mesmos parâmetros usados porsklearn.ensemble.RandomForestClassifier.
Exemplo de implementação
No exemplo a seguir, estamos construindo um regressor de floresta aleatório usando sklearn.ensemble.RandomForestregressor e também prever para novos valores usando o método predict ().
from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
RFregr = RandomForestRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
RFregr.fit(X, y)Resultado
RandomForestRegressor(
bootstrap = True, criterion = 'mse', max_depth = 10,
max_features = 'auto', max_leaf_nodes = None,
min_impurity_decrease = 0.0, min_impurity_split = None,
min_samples_leaf = 1, min_samples_split = 2,
min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
oob_score = False, random_state = 0, verbose = 0, warm_start = False
)Uma vez ajustados, podemos prever a partir do modelo de regressão da seguinte forma -
print(RFregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Resultado
[98.47729198]Métodos Extra-Árvore
Para cada recurso em consideração, ele seleciona um valor aleatório para a divisão. A vantagem de usar métodos de árvore extras é que isso permite reduzir um pouco mais a variância do modelo. A desvantagem de usar esses métodos é que aumenta ligeiramente o viés.
Classificação com Método Extra-Árvore
Para criar um classificador usando o método Extra-tree, o módulo Scikit-learn fornece sklearn.ensemble.ExtraTreesClassifier. Ele usa os mesmos parâmetros usados porsklearn.ensemble.RandomForestClassifier. A única diferença está na maneira, discutida acima, eles constroem árvores.
Exemplo de implementação
No exemplo a seguir, estamos construindo um classificador de floresta aleatório usando sklearn.ensemble.ExtraTreeClassifier e também verificando sua precisão usando cross_val_score módulo.
from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import ExtraTreesClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers=100,random_state = 0)
ETclf = ExtraTreesClassifier(n_estimators = 10,max_depth = None,min_samples_split = 10, random_state = 0)
scores = cross_val_score(ETclf, X, y, cv = 5)
scores.mean()Resultado
1.0Exemplo
Também podemos usar o conjunto de dados sklearn para construir o classificador usando o método Extra-Tree. Como no exemplo a seguir, estamos usando o conjunto de dados Pima-Indian.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 7
kfold = KFold(n_splits=10, random_state=seed)
num_trees = 150
max_features = 5
ETclf = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)
results = cross_val_score(ETclf, X, Y, cv=kfold)
print(results.mean())Resultado
0.7551435406698566Regressão com Método Extra-Árvore
Para criar um Extra-Tree regressão, o módulo Scikit-learn fornece sklearn.ensemble.ExtraTreesRegressor. Ao construir um regressor de floresta aleatório, ele usará os mesmos parâmetros usados porsklearn.ensemble.ExtraTreesClassifier.
Exemplo de implementação
No exemplo a seguir, estamos aplicando sklearn.ensemble.ExtraTreesregressore nos mesmos dados que usamos ao criar o regressor de floresta aleatório. Vamos ver a diferença na saída
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ETregr = ExtraTreesRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
ETregr.fit(X, y)Resultado
ExtraTreesRegressor(bootstrap = False, criterion = 'mse', max_depth = 10,
max_features = 'auto', max_leaf_nodes = None,
min_impurity_decrease = 0.0, min_impurity_split = None,
min_samples_leaf = 1, min_samples_split = 2,
min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
oob_score = False, random_state = 0, verbose = 0, warm_start = False)Exemplo
Uma vez ajustados, podemos prever a partir do modelo de regressão da seguinte forma -
print(ETregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Resultado
[85.50955817]Neste capítulo, aprenderemos sobre os métodos de reforço no Sklearn, que permitem construir um modelo de conjunto.
Os métodos de reforço constroem o modelo de conjunto de forma incremental. O princípio principal é construir o modelo de forma incremental, treinando cada estimador de modelo de base sequencialmente. Para construir um conjunto poderoso, esses métodos combinam basicamente vários alunos semanais que são treinados sequencialmente em várias iterações de dados de treinamento. O módulo sklearn.ensemble segue dois métodos de reforço.
AdaBoost
É um dos métodos de conjunto de boosting de maior sucesso, cuja chave principal está na maneira como eles atribuem pesos às instâncias no dataset. É por isso que o algoritmo precisa prestar menos atenção às instâncias ao construir modelos subsequentes.
Classificação com AdaBoost
Para criar um classificador AdaBoost, o módulo Scikit-learn fornece sklearn.ensemble.AdaBoostClassifier. Ao construir este classificador, o parâmetro principal que este módulo usa ébase_estimator. Aqui, base_estimator é o valor dobase estimatora partir do qual o conjunto amplificado é construído. Se escolhermos o valor deste parâmetro para nenhum, então, o estimador de base seriaDecisionTreeClassifier(max_depth=1).
Exemplo de implementação
No exemplo a seguir, estamos construindo um classificador AdaBoost usando sklearn.ensemble.AdaBoostClassifier e também prever e verificar sua pontuação.
from sklearn.ensemble import AdaBoostClassifier
from sklearn.datasets import make_classification
X, y = make_classification(n_samples = 1000, n_features = 10,n_informative = 2, n_redundant = 0,random_state = 0, shuffle = False)
ADBclf = AdaBoostClassifier(n_estimators = 100, random_state = 0)
ADBclf.fit(X, y)Resultado
AdaBoostClassifier(algorithm = 'SAMME.R', base_estimator = None,
learning_rate = 1.0, n_estimators = 100, random_state = 0)Exemplo
Uma vez ajustados, podemos prever para novos valores da seguinte forma -
print(ADBclf.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Resultado
[1]Exemplo
Agora podemos verificar a pontuação da seguinte forma -
ADBclf.score(X, y)Resultado
0.995Exemplo
Também podemos usar o conjunto de dados sklearn para construir o classificador usando o método Extra-Tree. Por exemplo, em um exemplo dado abaixo, estamos usando o conjunto de dados Pima-Indian.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = AdaBoostClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())Resultado
0.7851435406698566Regressão com AdaBoost
Para criar um regressor com o método Ada Boost, a biblioteca Scikit-learn fornece sklearn.ensemble.AdaBoostRegressor. Ao construir o regressor, ele usará os mesmos parâmetros usados porsklearn.ensemble.AdaBoostClassifier.
Exemplo de implementação
No exemplo a seguir, estamos construindo um regressor AdaBoost usando sklearn.ensemble.AdaBoostregressor e também prever para novos valores usando o método predict ().
from sklearn.ensemble import AdaBoostRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ADBregr = RandomForestRegressor(random_state = 0,n_estimators = 100)
ADBregr.fit(X, y)Resultado
AdaBoostRegressor(base_estimator = None, learning_rate = 1.0, loss = 'linear',
n_estimators = 100, random_state = 0)Exemplo
Uma vez ajustados, podemos prever a partir do modelo de regressão da seguinte forma -
print(ADBregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))Resultado
[85.50955817]Gradient Tree Boosting
Também é chamado Gradient Boosted Regression Trees(GRBT). É basicamente uma generalização do impulso para funções de perda diferenciáveis arbitrárias. Ele produz um modelo de previsão na forma de um conjunto de modelos de previsão da semana. Pode ser usado para problemas de regressão e classificação. Sua principal vantagem reside no fato de que eles lidam naturalmente com os dados de tipo misto.
Classificação com Gradient Tree Boost
Para criar um classificador Gradient Tree Boost, o módulo Scikit-learn fornece sklearn.ensemble.GradientBoostingClassifier. Ao construir este classificador, o parâmetro principal que este módulo usa é 'perda'. Aqui, 'perda' é o valor da função de perda a ser otimizado. Se escolhermos perda = desvio, ele se refere ao desvio para classificação com resultados probabilísticos.
Por outro lado, se escolhermos o valor deste parâmetro para exponencial, ele recupera o algoritmo AdaBoost. O parâmetron_estimatorscontrolará o número de alunos semanais. Um hiperparâmetro chamadolearning_rate (na faixa de (0,0, 1,0]) controlará o sobreajuste via encolhimento.
Exemplo de implementação
No exemplo a seguir, estamos construindo um classificador Gradient Boosting usando sklearn.ensemble.GradientBoostingClassifier. Estamos equipando este classificador com alunos de 50 semanas.
from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier
X, y = make_hastie_10_2(random_state = 0)
X_train, X_test = X[:5000], X[5000:]
y_train, y_test = y[:5000], y[5000:]
GDBclf = GradientBoostingClassifier(n_estimators = 50, learning_rate = 1.0,max_depth = 1, random_state = 0).fit(X_train, y_train)
GDBclf.score(X_test, y_test)Resultado
0.8724285714285714Exemplo
Também podemos usar o conjunto de dados sklearn para construir o classificador usando o Gradient Boosting Classifier. Como no exemplo a seguir, estamos usando o conjunto de dados Pima-Indian.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = GradientBoostingClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())Resultado
0.7946582356674234Regressão com Gradient Tree Boost
Para criar um regressor com o método Gradient Tree Boost, a biblioteca Scikit-learn fornece sklearn.ensemble.GradientBoostingRegressor. Ele pode especificar a função de perda para regressão por meio da perda do nome do parâmetro. O valor padrão para perda é 'ls'.
Exemplo de implementação
No exemplo a seguir, estamos construindo um regressor Gradient Boosting usando sklearn.ensemble.GradientBoostingregressor e também encontrar o erro quadrático médio usando o método mean_squared_error ().
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor
X, y = make_friedman1(n_samples = 2000, random_state = 0, noise = 1.0)
X_train, X_test = X[:1000], X[1000:]
y_train, y_test = y[:1000], y[1000:]
GDBreg = GradientBoostingRegressor(n_estimators = 80, learning_rate=0.1,
max_depth = 1, random_state = 0, loss = 'ls').fit(X_train, y_train)Uma vez ajustado, podemos encontrar o erro quadrático médio da seguinte forma -
mean_squared_error(y_test, GDBreg.predict(X_test))Resultado
5.391246106657164Aqui, estudaremos sobre os métodos de agrupamento no Sklearn que ajudarão na identificação de qualquer semelhança nas amostras de dados.
Métodos de agrupamento, um dos métodos de ML não supervisionados mais úteis, usados para encontrar padrões de similaridade e relacionamento entre amostras de dados. Depois disso, eles agrupam essas amostras em grupos com semelhanças com base nos recursos. O agrupamento determina o agrupamento intrínseco entre os dados não rotulados presentes, por isso é importante.
A biblioteca Scikit-learn tem sklearn.clusterpara realizar o agrupamento de dados não rotulados. Sob este módulo, o scikit-leran tem os seguintes métodos de agrupamento -
KMeans
Este algoritmo calcula os centróides e itera até encontrar o centróide ideal. Exige que o número de clusters seja especificado, por isso assume que eles já são conhecidos. A lógica principal desse algoritmo é agrupar os dados separando as amostras em n números de grupos de variâncias iguais, minimizando os critérios conhecidos como inércia. O número de clusters identificados pelo algoritmo é representado por 'K.
Scikit-learn tem sklearn.cluster.KMeansmódulo para realizar clustering K-Means. Enquanto calcula os centros de cluster e o valor da inércia, o parâmetro denominadosample_weight permite sklearn.cluster.KMeans módulo para atribuir mais peso a algumas amostras.
Propagação de afinidade
Este algoritmo é baseado no conceito de 'passagem de mensagens' entre diferentes pares de amostras até a convergência. Não requer que o número de clusters seja especificado antes de executar o algoritmo. O algoritmo tem uma complexidade de tempo da ordem (2), que é a maior desvantagem dele.
Scikit-learn tem sklearn.cluster.AffinityPropagation módulo para realizar clustering de Propagação de Afinidade.
Desvio Médio
Este algoritmo descobre principalmente blobsem uma densidade uniforme de amostras. Ele atribui os pontos de dados aos clusters iterativamente, mudando os pontos em direção à densidade mais alta de pontos de dados. Em vez de confiar em um parâmetro chamadobandwidth ditando o tamanho da região a ser pesquisada, ele define automaticamente o número de clusters.
Scikit-learn tem sklearn.cluster.MeanShift módulo para realizar agrupamento de deslocamento médio.
Agrupamento espectral
Antes do agrupamento, esse algoritmo basicamente usa os autovalores, ou seja, o espectro da matriz de similaridade dos dados para realizar a redução de dimensionalidade em menos dimensões. O uso deste algoritmo não é aconselhável quando houver grande número de clusters.
Scikit-learn tem sklearn.cluster.SpectralClustering módulo para realizar clustering espectral.
Agrupamento hierárquico
Esse algoritmo cria clusters aninhados mesclando ou dividindo os clusters sucessivamente. Esta hierarquia de cluster é representada como dendrograma, ou seja, árvore. Ele se enquadra nas seguintes duas categorias -
Agglomerative hierarchical algorithms- Nesse tipo de algoritmo hierárquico, cada ponto de dados é tratado como um único cluster. Em seguida, aglomera sucessivamente os pares de cachos. Isso usa a abordagem de baixo para cima.
Divisive hierarchical algorithms- Neste algoritmo hierárquico, todos os pontos de dados são tratados como um grande cluster. Neste processo, o agrupamento envolve a divisão, usando a abordagem de cima para baixo, o grande cluster em vários pequenos clusters.
Scikit-learn tem sklearn.cluster.AgglomerativeClustering módulo para realizar clustering hierárquico aglomerativo.
DBSCAN
Ele significa “Density-based spatial clustering of applications with noise”. Este algoritmo é baseado na noção intuitiva de “clusters” e “ruído” de que os clusters são regiões densas de menor densidade no espaço de dados, separadas por regiões de menor densidade de pontos de dados.
Scikit-learn tem sklearn.cluster.DBSCANmódulo para realizar clustering DBSCAN. Existem dois parâmetros importantes, nomeadamente min_samples e eps, usados por este algoritmo para definir denso.
Maior valor do parâmetro min_samples ou o valor inferior do parâmetro eps dará uma indicação sobre a maior densidade de pontos de dados que é necessária para formar um cluster.
ÓPTICA
Ele significa “Ordering points to identify the clustering structure”. Este algoritmo também encontra clusters baseados em densidade em dados espaciais. Sua lógica básica de trabalho é como DBSCAN.
Ele aborda uma das principais fraquezas do algoritmo DBSCAN - o problema de detectar clusters significativos em dados de densidade variável - ordenando os pontos do banco de dados de forma que os pontos espacialmente mais próximos se tornem vizinhos no ordenamento.
Scikit-learn tem sklearn.cluster.OPTICS módulo para realizar agrupamento OPTICS.
BÉTULA
Significa redução iterativa balanceada e agrupamento usando hierarquias. É usado para realizar clustering hierárquico em grandes conjuntos de dados. Ele constrói uma árvore chamadaCFT ie Characteristics Feature Tree, para os dados fornecidos.
A vantagem do CFT é que os nós de dados chamados de nós CF (Characteristics Feature) contêm as informações necessárias para o agrupamento, o que evita ainda mais a necessidade de manter todos os dados de entrada na memória.
Scikit-learn tem sklearn.cluster.Birch módulo para executar clustering BIRCH.
Comparando Algoritmos de Clustering
A tabela a seguir fornecerá uma comparação (com base em parâmetros, escalabilidade e métrica) dos algoritmos de agrupamento no scikit-learn.
| Sr. Não | Nome do Algoritmo | Parâmetros | Escalabilidade | Métrica usada |
|---|---|---|---|---|
| 1 | K-Means | No. de clusters | Amostras n muito grandes | A distância entre os pontos. |
| 2 | Propagação de afinidade | Amortecimento | Não é escalável com n_samples | Distância do Gráfico |
| 3 | Mean-Shift | Largura de banda | Não é escalonável com n_samples. | A distância entre os pontos. |
| 4 | Agrupamento espectral | No. de clusters | Nível médio de escalabilidade com n_samples. Pequeno nível de escalabilidade com n_clusters. | Distância do Gráfico |
| 5 | Agrupamento hierárquico | Limite de distância ou número de clusters | Amostras n grandes n_clusters grandes | A distância entre os pontos. |
| 6 | DBSCAN | Tamanho da vizinhança | Amostras n muito grandes e n_clusters médios. | Distância do ponto mais próximo |
| 7 | ÓPTICA | Associação mínima do cluster | N_samples muito grandes e n_clusters grandes. | A distância entre os pontos. |
| 8 | BÉTULA | Limiar, fator de ramificação | Amostras n grandes n_clusters grandes | A distância euclidiana entre pontos. |
Clustering K-Means no conjunto de dados Scikit-learn Digit
Neste exemplo, aplicaremos o agrupamento K-means no conjunto de dados de dígitos. Este algoritmo identificará dígitos semelhantes sem usar as informações do rótulo original. A implementação é feita no notebook Jupyter.
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shapeResultado
1797, 64)Esta saída mostra que o conjunto de dados de dígitos está tendo 1797 amostras com 64 recursos.
Exemplo
Agora, execute o agrupamento K-Means da seguinte forma -
kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shapeResultado
(10, 64)Esta saída mostra que o clustering K-means criou 10 clusters com 64 recursos.
Exemplo
fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks = [], yticks = [])
axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)Resultado
A saída abaixo tem imagens mostrando centros de clusters aprendidos por K-Means Clustering.

Em seguida, o script Python abaixo irá combinar os rótulos de cluster aprendidos (por K-Means) com os rótulos verdadeiros encontrados neles -
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]Também podemos verificar a precisão com a ajuda do comando mencionado abaixo.
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)Resultado
0.7935447968836951Exemplo de implementação completo
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape
fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks = [])
axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)Existem várias funções com a ajuda das quais podemos avaliar o desempenho de algoritmos de agrupamento.
A seguir estão algumas funções importantes e mais usadas fornecidas pelo Scikit-learn para avaliar o desempenho do cluster -
Índice Rand Ajustado
Rand Index é uma função que calcula uma medida de similaridade entre dois agrupamentos. Para este cálculo, o índice rand considera todos os pares de amostras e pares de contagem que são atribuídos nos clusters semelhantes ou diferentes no clustering predito e verdadeiro. Posteriormente, a pontuação do Índice Rand bruto é "ajustada para o acaso" na pontuação do Índice Rand Ajustado usando a seguinte fórmula -
$$Adjusted\:RI=\left(RI-Expected_{-}RI\right)/\left(max\left(RI\right)-Expected_{-}RI\right)$$Tem dois parâmetros a saber labels_true, que são rótulos de classe de verdade fundamental, e labels_pred, que são rótulos de clusters a serem avaliados.
Exemplo
from sklearn.metrics.cluster import adjusted_rand_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
adjusted_rand_score(labels_true, labels_pred)Resultado
0.4444444444444445A rotulagem perfeita seria avaliada como 1 e a rotulagem incorreta ou independente seria classificada como 0 ou negativa.
Pontuação baseada em informações mútuas
Informação mútua é uma função que calcula a concordância das duas atribuições. Ele ignora as permutações. Existem as seguintes versões disponíveis -
Informação mútua normalizada (NMI)
Scikit aprender tem sklearn.metrics.normalized_mutual_info_score módulo.
Exemplo
from sklearn.metrics.cluster import normalized_mutual_info_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
normalized_mutual_info_score (labels_true, labels_pred)Resultado
0.7611702597222881Informações mútuas ajustadas (AMI)
Scikit aprender tem sklearn.metrics.adjusted_mutual_info_score módulo.
Exemplo
from sklearn.metrics.cluster import adjusted_mutual_info_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
adjusted_mutual_info_score (labels_true, labels_pred)Resultado
0.4444444444444448Pontuação de Fowlkes-Mallows
A função Fowlkes-Mallows mede a similaridade de dois agrupamentos de um conjunto de pontos. Pode ser definido como a média geométrica da precisão e recuperação dos pares.
Matematicamente,
$$FMS=\frac{TP}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)}}$$Aqui, TP = True Positive - número de pares de pontos pertencentes aos mesmos clusters em rótulos verdadeiros e preditos.
FP = False Positive - número de pares de pontos pertencentes aos mesmos clusters em rótulos verdadeiros, mas não nos rótulos previstos.
FN = False Negative - número de pares de pontos pertencentes aos mesmos clusters nos rótulos previstos, mas não nos rótulos verdadeiros.
O Scikit learn tem o módulo sklearn.metrics.fowlkes_mallows_score -
Exemplo
from sklearn.metrics.cluster import fowlkes_mallows_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
fowlkes_mallows__score (labels_true, labels_pred)Resultado
0.6546536707079771Coeficiente de silhueta
A função Silhouette calculará o Coeficiente Silhouette médio de todas as amostras usando a distância intra-cluster média e a distância média do cluster mais próximo para cada amostra.
Matematicamente,
$$S=\left(b-a\right)/max\left(a,b\right)$$Aqui, a é a distância intra-cluster.
e, b é a distância média do cluster mais próximo.
O Scikit aprender tem sklearn.metrics.silhouette_score módulo -
Exemplo
from sklearn import metrics.silhouette_score
from sklearn.metrics import pairwise_distances
from sklearn import datasets
import numpy as np
from sklearn.cluster import KMeans
dataset = datasets.load_iris()
X = dataset.data
y = dataset.target
kmeans_model = KMeans(n_clusters = 3, random_state = 1).fit(X)
labels = kmeans_model.labels_
silhouette_score(X, labels, metric = 'euclidean')Resultado
0.5528190123564091Matriz de Contingência
Esta matriz relatará a cardinalidade de interseção para cada par confiável de (verdadeiro, previsto). A matriz de confusão para problemas de classificação é uma matriz de contingência quadrada.
O Scikit aprender tem sklearn.metrics.contingency_matrix módulo.
Exemplo
from sklearn.metrics.cluster import contingency_matrix
x = ["a", "a", "a", "b", "b", "b"]
y = [1, 1, 2, 0, 1, 2]
contingency_matrix(x, y)Resultado
array([
[0, 2, 1],
[1, 1, 1]
])A primeira linha da saída acima mostra que entre três amostras cujo verdadeiro cluster é “a”, nenhuma delas está em 0, duas delas estão em 1 e 1 está em 2. Por outro lado, a segunda linha mostra que entre três amostras cujo verdadeiro cluster é “b”, 1 está em 0, 1 está em 1 e 1 está em 2.
Redução de dimensionalidade, um método de aprendizado de máquina não supervisionado é usado para reduzir o número de variáveis de recurso para cada amostra de dados selecionando um conjunto de recursos principais. A Análise de Componentes Principais (PCA) é um dos algoritmos populares para redução de dimensionalidade.
PCA Exato
Principal Component Analysis (PCA) é usado para redução de dimensionalidade linear usando Singular Value Decomposition(SVD) dos dados para projetá-los em um espaço dimensional inferior. Durante a decomposição usando PCA, os dados de entrada são centralizados, mas não escalados para cada recurso antes de aplicar o SVD.
A biblioteca de ML Scikit-learn fornece sklearn.decomposition.PCAmódulo que é implementado como um objeto transformador que aprende n componentes em seu método fit (). Ele também pode ser usado em novos dados para projetá-los nesses componentes.
Exemplo
O exemplo a seguir usará o módulo sklearn.decomposition.PCA para encontrar os 5 melhores componentes principais do conjunto de dados Pima Indians Diabetes.
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', ‘class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 5)
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)Resultado
Explained Variance: [0.88854663 0.06159078 0.02579012 0.01308614 0.00744094]
[
[-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
[-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
[-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
[ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
]PCA incremental
Incremental Principal Component Analysis (IPCA) é usado para resolver a maior limitação da Análise de Componentes Principais (PCA) e que é o PCA suporta apenas processamento em lote, significa que todos os dados de entrada a serem processados devem caber na memória.
A biblioteca de ML Scikit-learn fornece sklearn.decomposition.IPCA módulo que torna possível implementar Out-of-Core PCA usando seu partial_fit método em blocos de dados buscados sequencialmente ou habilitando o uso de np.memmap, um arquivo mapeado na memória, sem carregar o arquivo inteiro na memória.
Da mesma forma que o PCA, durante a decomposição usando IPCA, os dados de entrada são centralizados, mas não escalados para cada recurso antes de aplicar o SVD.
Exemplo
O exemplo a seguir usará sklearn.decomposition.IPCA módulo no conjunto de dados de dígitos Sklearn.
from sklearn.datasets import load_digits
from sklearn.decomposition import IncrementalPCA
X, _ = load_digits(return_X_y = True)
transformer = IncrementalPCA(n_components = 10, batch_size = 100)
transformer.partial_fit(X[:100, :])
X_transformed = transformer.fit_transform(X)
X_transformed.shapeResultado
(1797, 10)Aqui, podemos caber parcialmente em lotes menores de dados (como fizemos em 100 por lote) ou você pode deixar o fit() função para dividir os dados em lotes.
Kernel PCA
A análise de componentes principais do kernel, uma extensão do PCA, atinge a redução da dimensionalidade não linear usando kernels. Suporta ambostransform and inverse_transform.
A biblioteca de ML Scikit-learn fornece sklearn.decomposition.KernelPCA módulo.
Exemplo
O exemplo a seguir usará sklearn.decomposition.KernelPCAmódulo no conjunto de dados de dígitos Sklearn. Estamos usando kernel sigmóide.
from sklearn.datasets import load_digits
from sklearn.decomposition import KernelPCA
X, _ = load_digits(return_X_y = True)
transformer = KernelPCA(n_components = 10, kernel = 'sigmoid')
X_transformed = transformer.fit_transform(X)
X_transformed.shapeResultado
(1797, 10)PCA usando SVD randomizado
A Análise de Componente Principal (PCA) usando SVD aleatório é usada para projetar dados para um espaço de dimensão inferior preservando a maior parte da variância, eliminando o vetor singular de componentes associados a valores singulares inferiores. Aqui osklearn.decomposition.PCA módulo com o parâmetro opcional svd_solver=’randomized’ vai ser muito útil.
Exemplo
O exemplo a seguir usará sklearn.decomposition.PCA módulo com o parâmetro opcional svd_solver = 'randomized' para encontrar os melhores 7 componentes principais do conjunto de dados Pima Indians Diabetes.
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 7,svd_solver = 'randomized')
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)Resultado
Explained Variance: [8.88546635e-01 6.15907837e-02 2.57901189e-02 1.30861374e-027.44093864e-03 3.02614919e-03 5.12444875e-04]
[
[-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
[-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
[-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
[ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
[-5.04730888e-03 5.07391813e-02 7.56365525e-02 2.21363068e-01-6.13326472e-03 -9.70776708e-01 -2.02903702e-03 -1.51133239e-02]
[ 9.86672995e-01 8.83426114e-04 -1.22975947e-03 -3.76444746e-041.42307394e-03 -2.73046214e-03 -6.34402965e-03 -1.62555343e-01]
]