Принципы спутниковой связи
А satellite это тело, которое движется вокруг другого тела математически предсказуемым путем, называемым Orbit. Спутник связи - это не что иное, как микроволновая ретрансляторная станция в космосе, которая используется в телекоммуникациях, радио и телевидении наряду с интернет-приложениями.
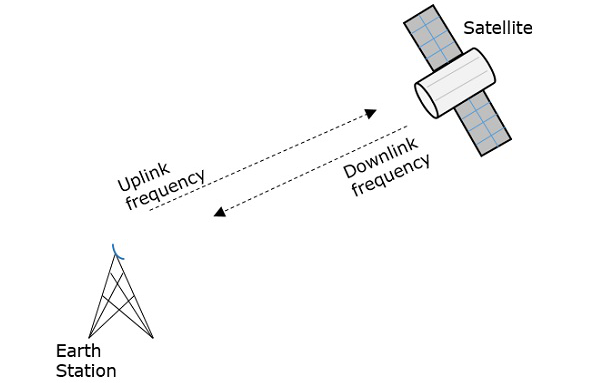
А repeaterпредставляет собой схему, которая увеличивает мощность принимаемого сигнала и повторно передает его. Но здесь этот ретранслятор работает какtransponder, который изменяет полосу частот передаваемого сигнала от принятой.
Частота, с которой сигнал отправляется в пространство, называется Uplink frequency, а частота, с которой он отправляется транспондером, равна Downlink frequency.
Следующий рисунок ясно иллюстрирует эту концепцию.
Теперь давайте посмотрим на преимущества, недостатки и приложения спутниковой связи.
Спутниковая связь - преимущества
Есть много преимуществ спутниковой связи, таких как:
Flexibility
Легкость установки новых схем
Расстояния легко преодолеваются, а стоимость не имеет значения
Возможности трансляции
Каждый уголок земли покрыт
Пользователь может управлять сетью
Спутниковая связь - недостатки
Спутниковая связь имеет следующие недостатки -
Первоначальные затраты, такие как затраты на сегмент и запуск, слишком высоки.
Перегруженность частот
Помехи и распространение
Спутниковая связь - Приложения
Спутниковая связь находит свое применение в следующих областях -
В радиовещании.
В телевещании, например, DTH.
В интернет-приложениях, таких как подключение к Интернету для передачи данных, приложения GPS, просмотр веб-страниц и т. Д.
Для голосовой связи.
Для сектора исследований и разработок во многих областях.
В военных приложениях и навигации.
Ориентация спутника на его орбите зависит от трех законов, называемых законами Кеплера.
Законы Кеплера
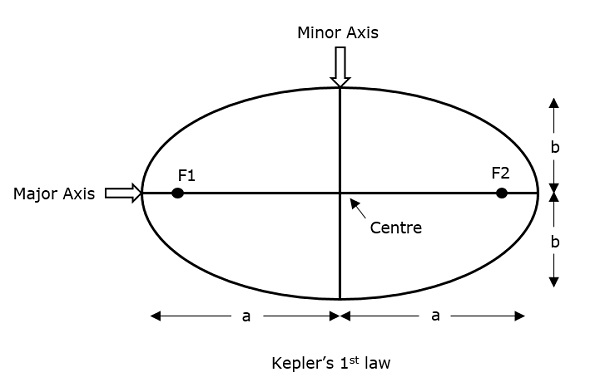
Иоганн Кеплер (1571-1630), ученый-астроном, дал 3 революционных закона, касающихся движения спутников. Путь, по которому следует спутник вокруг своей главной (Земли), являетсяellipse. Эллипс имеет два фокуса -F1 и F2Земля является одним из них.
Если рассматривать расстояние от центра объекта до точки на его эллиптическом пути, то самая дальняя точка эллипса от центра называется apogee а самая короткая точка эллипса от центра называется perigee.
1- й закон Кеплера
1 Кеплер й государства закона , что «каждая планета вращается вокруг Солнца по эллиптической орбите, с солнцем , как один из его фокусов». Таким образом, спутник движется по эллиптической траектории с Землей в качестве одного из его фокусов.
Большая полуось эллипса обозначается как 'a'и малая полуось обозначается как b. Следовательно, эксцентриситет e этой системы можно записать как -
$$ e = \ frac {\ sqrt {a ^ {2} -b ^ {2}}} {a} $$
Eccentricity (e) - Это параметр, который определяет разницу в форме эллипса, а не круга.
Semi-major axis (a) - Это самый длинный диаметр, соединяющий два фокуса по центру, который касается обоих апогеев (самых дальних от центра точек эллипса).
Semi-minor axis (b) - Это самый короткий диаметр, проведенный через центр, который касается обеих перигеев (самые короткие точки эллипса от центра).
Они хорошо описаны на следующем рисунке.
Для эллиптической траектории всегда желательно, чтобы эксцентриситет находился в диапазоне от 0 до 1, то есть 0 <e <1, потому что если e становится равным нулю, путь больше не будет иметь эллиптическую форму, а будет преобразован в круговой путь.
2- й закон Кеплера
2- й закон Кеплера гласит, что «в течение равных промежутков времени площадь, покрываемая спутником, равна центру Земли».
Это можно понять, взглянув на следующий рисунок.
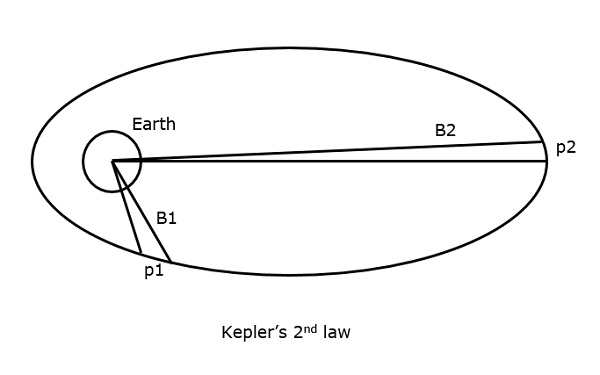
Предположим, что спутник покрывает p1 и p2 расстояния, в том же временном интервале, затем области B1 и B2 покрытые в обоих случаях соответственно, равны.
3- й закон Кеплера
Третий закон Кеплера гласит: «Квадрат периодического времени обращения по орбите пропорционален кубу среднего расстояния между двумя телами».
Математически это можно записать как
$$ T ^ {2} \: \ alpha \: \: a ^ {3} $$
Что подразумевает
$$ T ^ {2} = \ frac {4 \ pi ^ {2}} {GM} a ^ {3} $$
Где $ \ frac {4 \ pi ^ {2}} {GM} $ - константа пропорциональности (согласно ньютоновской механике)
$$ T ^ {2} = \ frac {4 \ pi ^ {2}} {\ mu} a ^ {3} $$
Где μ = геоцентрическая гравитационная постоянная Земли, т.е. Μ = 3,986005 × 10 14 м 3 / сек 2.
$$ 1 = \ left (\ frac {2 \ pi} {T} \ right) ^ {2} \ frac {a ^ {3}} {\ mu} $$
$$ 1 = n ^ {2} \ frac {a ^ {3}} {\ mu} \: \: \: \ Rightarrow \: \: \: a ^ {3} = \ frac {\ mu} {n ^ {2}} $$
где n = среднее движение спутника в радианах в секунду
Орбитальное функционирование спутников рассчитывается с помощью этих законов Кеплера.
Наряду с этим следует отметить еще одну важную вещь. Спутник, когда он вращается вокруг Земли, испытывает притягивающую силу со стороны Земли, которая является силой гравитации. Кроме того, он испытывает некоторую притягивающую силу от солнца и луны. Следовательно, на него действуют две силы. Они -
Centripetal force - Сила, которая стремится притягивать объект, движущийся по траектории, к себе, называется centripetal force.
Centrifugal force - Сила, которая стремится оттолкнуть объект, движущийся по траектории, от своего положения, называется centrifugal force.
Итак, спутник должен уравновесить эти две силы, чтобы оставаться на своей орбите.
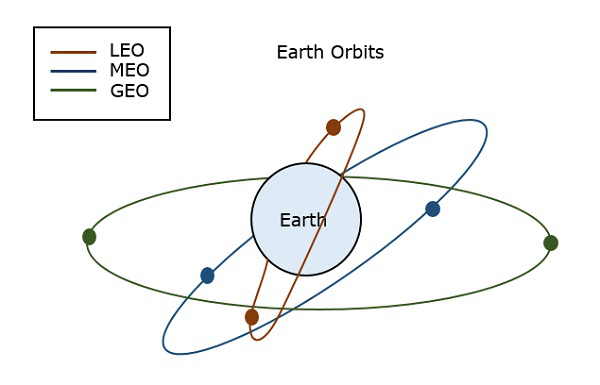
Орбиты Земли
Спутник, запускаемый в космос, должен быть помещен на определенную орбиту, чтобы обеспечить определенный путь для его вращения, чтобы поддерживать доступность и служить своей цели, будь то научная, военная или коммерческая. Такие орбиты, которые назначаются спутникам относительно Земли, называютсяEarth Orbits. Спутники на этих орбитах - Земля.Orbit Satellites.
Важными видами земных орбит являются:
Гео синхронная околоземная орбита
Средняя околоземная орбита
Низкая околоземная орбита
Спутники на геостационарной орбите
А Geo-Synchronous Earth Orbit (GEO)Спутник - это тот, который расположен на высоте 22 300 миль над Землей. Эта орбита синхронизирована сside real day(т.е. 23 часа 56 минут). Эта орбита можетhave inclination and eccentricity. Он не может быть круглым. Эта орбита может быть наклонена к полюсам Земли. Но при наблюдении с Земли он кажется неподвижным.
Та же геосинхронная орбита, если она круговая и в плоскости экватора, называется geo-stationary orbit. Эти спутники размещены на расстоянии 35 900 км / с (так же, как и геостационарные) над экватором Земли, и они продолжают вращаться относительно направления Земли (с запада на восток). Эти спутники считаются стационарными по отношению к Земле и, следовательно, следует из названия.
Гео-стационарные спутники на околоземной орбите используются для прогнозирования погоды, спутникового телевидения, спутникового радио и других видов глобальной связи.
На следующем рисунке показана разница между геосинхронными и геостационарными орбитами. Ось вращения указывает на движение Земли.
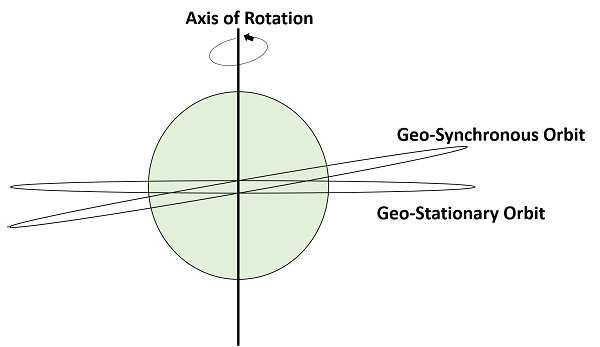
Note- Каждая геостационарная орбита является геосинхронной орбитой. Но каждая геосинхронная орбита НЕ является геостационарной орбитой.
Спутники на средней околоземной орбите
Medium Earth Orbit (MEO)спутниковые сети будут находиться на орбите на расстоянии около 8000 миль от поверхности Земли. Сигналы, передаваемые со спутника MEO, проходят меньшее расстояние. Это приводит к повышению уровня сигнала на приемной стороне. Это показывает, что на приемной стороне можно использовать более компактные и легкие приемные терминалы.
Поскольку сигнал распространяется на меньшее расстояние к спутнику и от него, задержка передачи меньше. Transmission delay можно определить как время, которое требуется сигналу, чтобы добраться до спутника и вернуться к принимающей станции.
Для связи в реальном времени чем короче задержка передачи, тем лучше будет система связи. Например, если спутнику GEO требуется 0,25 секунды для полета туда и обратно, то спутнику MEO требуется менее 0,1 секунды, чтобы совершить такой же рейс. СОО работает в диапазоне частот 2 ГГц и выше.
Спутники на низкой околоземной орбите
Спутники на низкой околоземной орбите (НОО) в основном подразделяются на три категории, а именно: маленькие НОО, большие НОО и Мега-НОО. НОО будут двигаться по орбите на расстоянии от 500 до 1000 миль над поверхностью Земли.
Это относительно небольшое расстояние сокращает задержку передачи до 0,05 секунды. Это дополнительно снижает потребность в чувствительном и громоздком приемном оборудовании. Маленькие LEO будут работать в диапазоне 800 МГц (0,8 ГГц). Большие LEO будут работать в диапазоне 2 ГГц или выше, а Mega-LEOs будут работать в диапазоне 20-30 ГГц.
Более высокие частоты, связанные с Mega-LEOs переводит в большую пропускную способность информации и уступает возможности схемы передачи видео с малой задержкой в реальном времени.
На следующем рисунке показаны пути LEO, MEO и GEO.