Python - разделяй и властвуй

В подходе «разделяй и властвуй» рассматриваемая проблема делится на более мелкие подзадачи, и затем каждая проблема решается независимо. Когда мы продолжаем разделять подзадачи на еще более мелкие подзадачи, мы можем в конечном итоге достичь стадии, когда разделение больше невозможно. Эти «атомарные» наименьшие возможные подзадачи (дроби) решены. Решение всех подзадач окончательно объединяется, чтобы получить решение исходной проблемы.

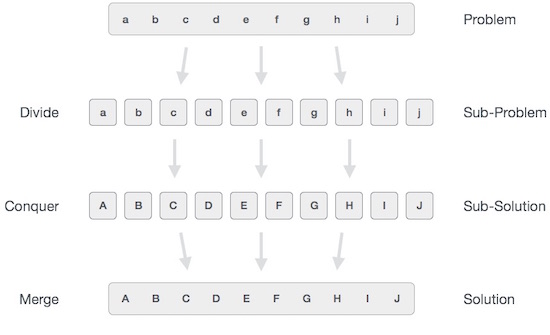
В широком смысле мы можем понять divide-and-conquer подход в трехэтапном процессе.

Разделить / Разбить

Этот шаг включает разбиение проблемы на более мелкие подзадачи. Подзадачи должны представлять собой часть исходной проблемы. На этом этапе обычно используется рекурсивный подход для разделения проблемы до тех пор, пока ни одна из подзадач не станет делимой. На этом этапе подзадачи становятся атомарными по своей природе, но все же представляют некоторую часть реальной проблемы.

Завоевать / Решить

На этом этапе необходимо решить множество более мелких подзадач. Обычно на этом уровне проблемы считаются «решенными» сами по себе.

Слияние / объединение

Когда более мелкие подзадачи решены, этот этап рекурсивно объединяет их, пока они не сформулируют решение исходной проблемы. Этот алгоритмический подход работает рекурсивно, и этапы "завоевать и объединить" работают настолько близко, что кажутся единым целым.

Примеры

Следующая программа является примером divide-and-conquer подход к программированию, при котором бинарный поиск реализован с использованием Python.

Реализация двоичного поиска

В бинарном поиске мы берем отсортированный список элементов и начинаем искать элемент в середине списка. Если значение поиска совпадает со средним значением в списке, мы завершаем поиск. В противном случае мы исключаем половину списка элементов, выбирая, обрабатывать ли правую или левую половину списка в зависимости от значения искомого элемента. Это возможно, поскольку список отсортирован, и это намного быстрее, чем линейный поиск. Здесь мы делим данный список и побеждаем, выбирая правильную половину списка. Повторяем этот подход до тех пор, пока не найдем элемент или не сделаем вывод о его отсутствии в списке.

def bsearch(list, val):

    list_size = len(list) - 1

    idx0 = 0
    idxn = list_size
# Find the middle most value

    while idx0 <= idxn:
        midval = (idx0 + idxn)// 2

        if list[midval] == val:
            return midval
# Compare the value the middle most value
        if val > list[midval]:
            idx0 = midval + 1
        else:
            idxn = midval - 1

    if idx0 > idxn:
        return None
# Initialize the sorted list
list = [2,7,19,34,53,72]

# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))

Когда приведенный выше код выполняется, он дает следующий результат:

5
None