TensorFlow - линейная регрессия
В этой главе мы сосредоточимся на базовом примере реализации линейной регрессии с использованием TensorFlow. Логистическая регрессия или линейная регрессия - это контролируемый подход машинного обучения для классификации дискретных категорий порядка. Наша цель в этой главе - построить модель, с помощью которой пользователь может предсказать взаимосвязь между переменными-предикторами и одной или несколькими независимыми переменными.
Связь между этими двумя переменными считается линейной. Если y является зависимой переменной, а x рассматривается как независимая переменная, то соотношение линейной регрессии двух переменных будет выглядеть следующим образом:
Y = Ax+bМы разработаем алгоритм линейной регрессии. Это позволит нам понять следующие две важные концепции -
- Функция стоимости
- Алгоритмы градиентного спуска
Схематическое изображение линейной регрессии упомянуто ниже -

Графический вид уравнения линейной регрессии упомянут ниже -
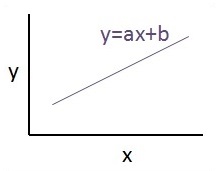
Шаги по разработке алгоритма линейной регрессии
Теперь мы узнаем о шагах, которые помогают в разработке алгоритма линейной регрессии.
Шаг 1
Важно импортировать необходимые модули для построения модуля линейной регрессии. Начинаем импортировать библиотеки Python NumPy и Matplotlib.
import numpy as np
import matplotlib.pyplot as pltШаг 2
Определите количество коэффициентов, необходимых для логистической регрессии.
number_of_points = 500
x_point = []
y_point = []
a = 0.22
b = 0.78Шаг 3
Итерируйте переменные для генерации 300 случайных точек по уравнению регрессии -
Y = 0,22x + 0,78
for i in range(number_of_points):
x = np.random.normal(0.0,0.5)
y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x])
y_point.append([y])Шаг 4
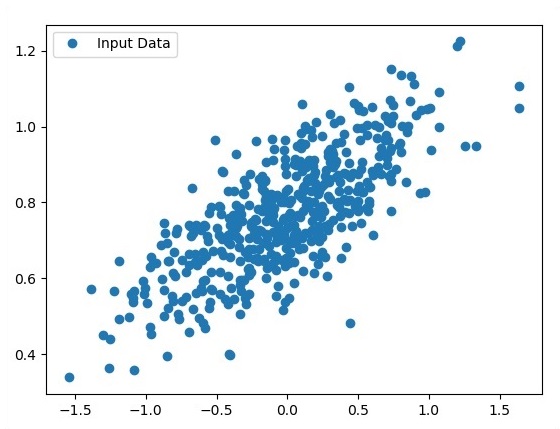
Просмотрите сгенерированные точки с помощью Matplotlib.
fplt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()Полный код для логистической регрессии выглядит следующим образом:
import numpy as np
import matplotlib.pyplot as plt
number_of_points = 500
x_point = []
y_point = []
a = 0.22
b = 0.78
for i in range(number_of_points):
x = np.random.normal(0.0,0.5)
y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x])
y_point.append([y])
plt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend()
plt.show()Количество точек, принимаемых в качестве входных данных, считается входными данными.