Apache MXNet - แพ็คเกจ Python
ในบทนี้เราจะเรียนรู้เกี่ยวกับแพ็คเกจ Python ที่มีอยู่ใน Apache MXNet
แพ็คเกจ MXNet Python ที่สำคัญ
MXNet มีแพ็คเกจ Python ที่สำคัญดังต่อไปนี้ซึ่งเราจะพูดถึงทีละรายการ -
Autograd (ความแตกต่างอัตโนมัติ)
NDArray
KVStore
Gluon
Visualization
ก่อนอื่นให้เราเริ่มต้นด้วย Autograd แพ็คเกจ Python สำหรับ Apache MXNet
Autograd
Autograd หมายถึง automatic differentiationใช้เพื่อ backpropagate การไล่ระดับสีจากเมตริกการสูญเสียกลับไปที่พารามิเตอร์แต่ละตัว นอกจาก backpropagation แล้วยังใช้วิธีการเขียนโปรแกรมแบบไดนามิกเพื่อคำนวณการไล่ระดับสีอย่างมีประสิทธิภาพ เรียกอีกอย่างว่าโหมดย้อนกลับความแตกต่างอัตโนมัติ เทคนิคนี้มีประสิทธิภาพมากในสถานการณ์ 'fan-in' ซึ่งพารามิเตอร์จำนวนมากมีผลต่อเมตริกการสูญเสียเพียงครั้งเดียว
การไล่ระดับสีคืออะไร?
การไล่ระดับสีเป็นปัจจัยพื้นฐานของกระบวนการฝึกอบรมเครือข่ายประสาทเทียม โดยพื้นฐานแล้วพวกเขาบอกเราว่าจะเปลี่ยนพารามิเตอร์ของเครือข่ายเพื่อปรับปรุงประสิทธิภาพได้อย่างไร
ดังที่เราทราบดีว่าเครือข่ายประสาทเทียม (NN) ประกอบด้วยตัวดำเนินการเช่นผลรวมผลิตภัณฑ์การชักและอื่น ๆ ตัวดำเนินการเหล่านี้สำหรับการคำนวณจะใช้พารามิเตอร์เช่นน้ำหนักในเมล็ด Convolution เราควรจะต้องหาค่าที่เหมาะสมที่สุดสำหรับพารามิเตอร์เหล่านี้และการไล่ระดับสีจะแสดงวิธีและนำเราไปสู่การแก้ปัญหาด้วย
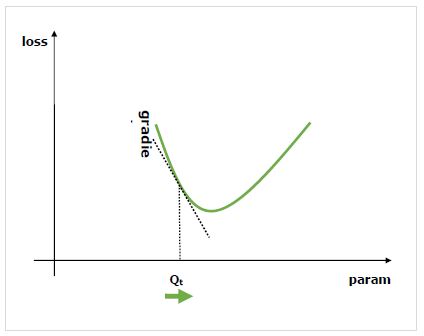
เราสนใจผลของการเปลี่ยนพารามิเตอร์ต่อประสิทธิภาพของเครือข่ายและการไล่ระดับสีบอกเราว่าตัวแปรที่ระบุเพิ่มขึ้นหรือลดลงเท่าใดเมื่อเราเปลี่ยนตัวแปรนั้นขึ้นอยู่กับ โดยปกติประสิทธิภาพจะถูกกำหนดโดยใช้เมตริกการสูญเสียที่เราพยายามลดให้เหลือน้อยที่สุด ตัวอย่างเช่นสำหรับการถดถอยเราอาจพยายามย่อให้เล็กที่สุดL2 การสูญเสียระหว่างการคาดการณ์และค่าที่แน่นอนของเราในขณะที่สำหรับการจัดประเภทเราอาจลดค่า cross-entropy loss.
เมื่อเราคำนวณการไล่ระดับสีของแต่ละพารามิเตอร์โดยอ้างอิงกับการสูญเสียแล้วเราสามารถใช้เครื่องมือเพิ่มประสิทธิภาพเช่นการไล่ระดับสีแบบสุ่ม
วิธีคำนวณการไล่ระดับสี?
เรามีตัวเลือกต่อไปนี้ในการคำนวณการไล่ระดับสี -
Symbolic Differentiation- ตัวเลือกแรกสุดคือ Symbolic Differentiation ซึ่งจะคำนวณสูตรสำหรับการไล่ระดับสีแต่ละครั้ง ข้อเสียเปรียบของวิธีนี้คือจะนำไปสู่สูตรที่ยาวอย่างไม่น่าเชื่อได้อย่างรวดเร็วเนื่องจากเครือข่ายมีความลึกและตัวดำเนินการมีความซับซ้อนมากขึ้น
Finite Differencing- อีกทางเลือกหนึ่งคือใช้ความแตกต่างแบบ จำกัด ซึ่งลองใช้ความแตกต่างเล็กน้อยในแต่ละพารามิเตอร์และดูว่าเมตริกการสูญเสียตอบสนองอย่างไร ข้อเสียเปรียบของวิธีนี้คือมันจะมีราคาแพงในการคำนวณและอาจมีความแม่นยำในการคำนวณต่ำ
Automatic differentiation- วิธีแก้ไขข้อเสียของวิธีการข้างต้นคือการใช้การสร้างความแตกต่างโดยอัตโนมัติเพื่อย้อนการไล่ระดับสีจากเมตริกการสูญเสียกลับไปยังพารามิเตอร์แต่ละตัว การขยายพันธุ์ช่วยให้เราสามารถใช้วิธีการเขียนโปรแกรมแบบไดนามิกเพื่อคำนวณการไล่ระดับสีได้อย่างมีประสิทธิภาพ วิธีนี้เรียกอีกอย่างว่าโหมดย้อนกลับความแตกต่างอัตโนมัติ
ความแตกต่างอัตโนมัติ (autograd)
ที่นี่เราจะเข้าใจรายละเอียดเกี่ยวกับการทำงานของ autograd โดยทั่วไปจะทำงานในสองขั้นตอนต่อไปนี้ -
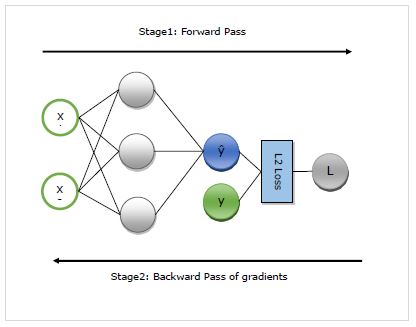
Stage 1 - เวทีนี้เรียกว่า ‘Forward Pass’ของการฝึกอบรม ตามความหมายของชื่อในขั้นตอนนี้จะสร้างบันทึกของตัวดำเนินการที่เครือข่ายใช้เพื่อทำการคาดคะเนและคำนวณเมตริกการสูญเสีย
Stage 2 - เวทีนี้เรียกว่า ‘Backward Pass’ของการฝึกอบรม ตามความหมายของชื่อในขั้นตอนนี้จะทำงานย้อนหลังผ่านบันทึกนี้ ย้อนกลับไปมันจะประเมินอนุพันธ์บางส่วนของแต่ละตัวดำเนินการกลับไปที่พารามิเตอร์เครือข่าย
ข้อดีของ autograd
ต่อไปนี้เป็นข้อดีของการใช้ Automatic Differentiation (autograd) -
Flexible- ความยืดหยุ่นที่ให้เราเมื่อกำหนดเครือข่ายของเราเป็นหนึ่งในประโยชน์มหาศาลของการใช้ autograd เราสามารถเปลี่ยนการดำเนินการในการทำซ้ำทุกครั้ง สิ่งเหล่านี้เรียกว่ากราฟไดนามิกซึ่งมีความซับซ้อนกว่ามากในการนำไปใช้ในกรอบงานที่ต้องใช้กราฟแบบคงที่ Autograd แม้ในกรณีดังกล่าวจะยังคงสามารถย้อนกลับการไล่ระดับสีได้อย่างถูกต้อง
Automatic- Autograd เป็นไปโดยอัตโนมัติกล่าวคือความซับซ้อนของกระบวนการ backpropagation จะได้รับการดูแลโดยคุณ เราต้องระบุว่าการไล่ระดับสีใดที่เราสนใจในการคำนวณ
Efficient - Autogard คำนวณการไล่ระดับสีได้อย่างมีประสิทธิภาพ
Can use native Python control flow operators- เราสามารถใช้ตัวดำเนินการควบคุมโฟลว์ Python ดั้งเดิมเช่น if condition และ while loop autograd จะยังคงสามารถ backpropagate การไล่ระดับสีได้อย่างมีประสิทธิภาพและถูกต้อง
ใช้ autograd ใน MXNet Gluon
ที่นี่ด้วยความช่วยเหลือของตัวอย่างเราจะดูว่าเราสามารถใช้งานได้อย่างไร autograd ใน MXNet Gluon
ตัวอย่างการใช้งาน
ในตัวอย่างต่อไปนี้เราจะใช้โมเดลการถดถอยที่มีสองชั้น หลังจากใช้งานแล้วเราจะใช้ autograd เพื่อคำนวณการไล่ระดับสีของการสูญเสียโดยอัตโนมัติโดยอ้างอิงกับพารามิเตอร์น้ำหนักแต่ละตัว -
ก่อนอื่นให้นำเข้า autogrard และแพ็คเกจอื่น ๆ ที่จำเป็นดังนี้ -
from mxnet import autograd
import mxnet as mx
from mxnet.gluon.nn import HybridSequential, Dense
from mxnet.gluon.loss import L2Lossตอนนี้เราต้องกำหนดเครือข่ายดังนี้ -
N_net = HybridSequential()
N_net.add(Dense(units=3))
N_net.add(Dense(units=1))
N_net.initialize()ตอนนี้เราต้องกำหนดความสูญเสียดังนี้ -
loss_function = L2Loss()ต่อไปเราต้องสร้างข้อมูลจำลองดังต่อไปนี้ -
x = mx.nd.array([[0.5, 0.9]])
y = mx.nd.array([[1.5]])ตอนนี้เราพร้อมแล้วสำหรับการส่งต่อครั้งแรกผ่านเครือข่าย เราต้องการให้ autograd บันทึกกราฟการคำนวณเพื่อที่เราจะได้คำนวณการไล่ระดับสี สำหรับสิ่งนี้เราจำเป็นต้องเรียกใช้รหัสเครือข่ายในขอบเขตของautograd.record บริบทดังต่อไปนี้ -
with autograd.record():
y_hat = N_net(x)
loss = loss_function(y_hat, y)ตอนนี้เราพร้อมแล้วสำหรับการส่งย้อนกลับซึ่งเราเริ่มต้นด้วยการเรียกวิธีการย้อนกลับในปริมาณที่น่าสนใจ จำนวนที่น่าสนใจในตัวอย่างของเราคือการสูญเสียเนื่องจากเราพยายามคำนวณการไล่ระดับสีของการสูญเสียโดยอ้างอิงกับพารามิเตอร์ -
loss.backward()ตอนนี้เรามีการไล่ระดับสีสำหรับแต่ละพารามิเตอร์ของเครือข่ายซึ่งเครื่องมือเพิ่มประสิทธิภาพจะใช้เพื่ออัปเดตค่าพารามิเตอร์เพื่อประสิทธิภาพที่ดีขึ้น ลองดูการไล่ระดับของเลเยอร์ที่ 1 ดังนี้ -
N_net[0].weight.grad()Output
ผลลัพธ์มีดังนี้
[[-0.00470527 -0.00846948]
[-0.03640365 -0.06552657]
[ 0.00800354 0.01440637]]
<NDArray 3x2 @cpu(0)>ตัวอย่างการใช้งานที่สมบูรณ์
ด้านล่างนี้เป็นตัวอย่างการใช้งานที่สมบูรณ์
from mxnet import autograd
import mxnet as mx
from mxnet.gluon.nn import HybridSequential, Dense
from mxnet.gluon.loss import L2Loss
N_net = HybridSequential()
N_net.add(Dense(units=3))
N_net.add(Dense(units=1))
N_net.initialize()
loss_function = L2Loss()
x = mx.nd.array([[0.5, 0.9]])
y = mx.nd.array([[1.5]])
with autograd.record():
y_hat = N_net(x)
loss = loss_function(y_hat, y)
loss.backward()
N_net[0].weight.grad()