Finite Automaton แบบไม่กำหนด

ใน NDFA สำหรับสัญลักษณ์อินพุตเฉพาะเครื่องสามารถย้ายไปที่สถานะใดก็ได้ในเครื่อง กล่าวอีกนัยหนึ่งไม่สามารถระบุสถานะที่แน่นอนที่เครื่องจักรเคลื่อนที่ได้ ดังนั้นจึงเรียกว่าNon-deterministic Automaton. เนื่องจากมีจำนวนสถานะ จำกัด เครื่องจึงถูกเรียกNon-deterministic Finite Machine หรือ Non-deterministic Finite Automaton.

คำจำกัดความอย่างเป็นทางการของ NDFA

NDFA สามารถแสดงด้วย 5-tuple (Q, ∑, δ, q ₀ , F) โดยที่ -

Q เป็นชุดของรัฐที่ จำกัด
∑ เป็นชุดสัญลักษณ์ จำกัด ที่เรียกว่าตัวอักษร
δคือฟังก์ชันการเปลี่ยนโดยที่δ: Q × ∑ → 2 ^Q

(ที่นี่ชุดกำลังของ Q (2 ^Q ) ถูกนำมาใช้เนื่องจากในกรณีของ NDFA จากสถานะการเปลี่ยนอาจเกิดขึ้นกับการรวมกันของสถานะ Q ใด ๆ )
q₀คือสถานะเริ่มต้นจากการประมวลผลอินพุตใด ๆ (q ₀ ∈ Q)
F คือชุดของสถานะสุดท้าย / สถานะของ Q (F ⊆ Q)

การแสดงกราฟิกของ NDFA: (เหมือนกับ DFA)

NDFA แสดงด้วย digraphs เรียกว่า state diagram

จุดยอดแสดงถึงสถานะ
ส่วนโค้งที่มีป้ายกำกับด้วยอักษรอินพุตแสดงการเปลี่ยน
สถานะเริ่มต้นแสดงด้วยส่วนโค้งขาเข้าเดี่ยวที่ว่างเปล่า
สถานะสุดท้ายถูกระบุด้วยวงกลมสองวง

Example

ให้หุ่นยนต์ จำกัด ที่ไม่ใช่ปัจจัยกำหนดเป็น→

ถาม = {a, b, c}
∑ = {0, 1}
q ₀ = {a}
F = {c}

ฟังก์ชันการเปลี่ยนแปลงδดังแสดงด้านล่าง -

สถานะปัจจุบัน	สถานะถัดไปสำหรับอินพุต 0	สถานะถัดไปสำหรับอินพุต 1
ก	ก, ข	ข
ข	ค	ก, ค
ค	ข, ค	ค

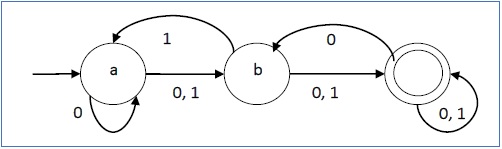
การแสดงกราฟิกจะเป็นดังนี้ -

DFA เทียบกับ NDFA

ตารางต่อไปนี้แสดงความแตกต่างระหว่าง DFA และ NDFA

DFA	NDFA
การเปลี่ยนจากสถานะเป็นสถานะถัดไปเฉพาะสำหรับสัญลักษณ์อินพุตแต่ละรายการ ดังนั้นจึงเรียกว่าดีเทอร์มินิสติก	การเปลี่ยนจากสถานะสามารถเป็นสถานะถัดไปได้หลายสถานะสำหรับสัญลักษณ์อินพุตแต่ละตัว ดังนั้นมันจะเรียกว่าไม่ใช่กำหนด
ไม่เห็นการเปลี่ยนสตริงว่างใน DFA	NDFA อนุญาตให้เปลี่ยนสตริงว่าง
อนุญาตให้มีการย้อนรอยใน DFA	ใน NDFA การย้อนรอยไม่สามารถทำได้เสมอไป
ต้องใช้พื้นที่มากขึ้น	ต้องการพื้นที่น้อย
DFA ยอมรับสตริงหากส่งผ่านไปยังสถานะสุดท้าย	NDFA ยอมรับสตริงหากการเปลี่ยนแปลงที่เป็นไปได้อย่างน้อยหนึ่งรายการสิ้นสุดในสถานะสุดท้าย