การเข้ารหัสคีย์สาธารณะ

ซึ่งแตกต่างจากการเข้ารหัสคีย์สมมาตรเราไม่พบการใช้การเข้ารหัสคีย์สาธารณะในอดีต เป็นแนวคิดที่ค่อนข้างใหม่

การเข้ารหัสแบบสมมาตรเหมาะอย่างยิ่งสำหรับองค์กรต่างๆเช่นรัฐบาลทหารและ บริษัท การเงินขนาดใหญ่ที่เกี่ยวข้องกับการสื่อสารประเภทต่างๆ

ด้วยการแพร่กระจายของเครือข่ายคอมพิวเตอร์ที่ไม่ปลอดภัยมากขึ้นในช่วงไม่กี่ทศวรรษที่ผ่านมาจึงมีความจำเป็นอย่างยิ่งที่จะต้องใช้การเข้ารหัสในระดับที่ใหญ่ขึ้น พบว่าคีย์สมมาตรไม่สามารถใช้งานได้จริงเนื่องจากความท้าทายที่ต้องเผชิญในการจัดการคีย์ สิ่งนี้ก่อให้เกิดระบบรหัสลับสาธารณะ

กระบวนการเข้ารหัสและถอดรหัสมีดังภาพต่อไปนี้ -

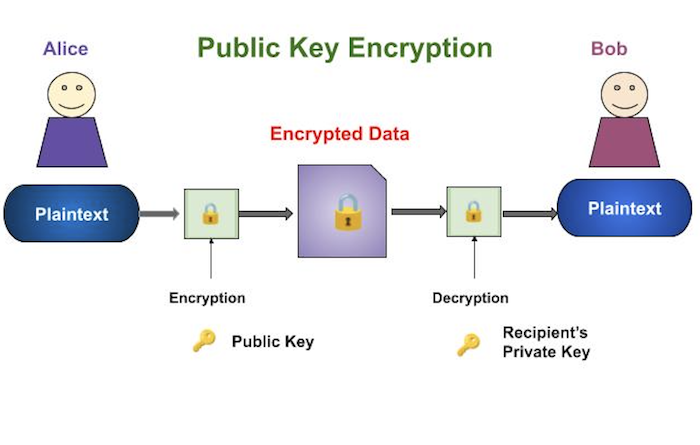
คุณสมบัติที่สำคัญที่สุดของรูปแบบการเข้ารหัสคีย์สาธารณะคือ -

ใช้คีย์ที่แตกต่างกันสำหรับการเข้ารหัสและถอดรหัส นี่คือคุณสมบัติที่กำหนดโครงร่างนี้แตกต่างจากโครงร่างการเข้ารหัสแบบสมมาตร
ผู้รับแต่ละคนมีคีย์การถอดรหัสที่ไม่ซ้ำกันโดยทั่วไปเรียกว่าคีย์ส่วนตัวของเขา
ผู้รับจำเป็นต้องเผยแพร่คีย์การเข้ารหัสซึ่งเรียกว่าคีย์สาธารณะของเขา
จำเป็นต้องมีการรับรองความถูกต้องของคีย์สาธารณะในโครงการนี้เพื่อหลีกเลี่ยงการปลอมแปลงโดยฝ่ายตรงข้ามเป็นผู้รับ โดยทั่วไป cryptosystem ประเภทนี้เกี่ยวข้องกับบุคคลที่สามที่เชื่อถือได้ซึ่งรับรองว่าคีย์สาธารณะนั้นเป็นของบุคคลหรือนิติบุคคลที่ระบุเท่านั้น
อัลกอริทึมการเข้ารหัสมีความซับซ้อนเพียงพอที่จะห้ามไม่ให้ผู้โจมตีอนุมานข้อความธรรมดาจากไซเฟอร์เท็กซ์และคีย์การเข้ารหัส (สาธารณะ)
แม้ว่าคีย์ส่วนตัวและคีย์สาธารณะจะเกี่ยวข้องกันทางคณิตศาสตร์ แต่ก็ไม่สามารถคำนวณคีย์ส่วนตัวจากคีย์สาธารณะได้ ในความเป็นจริงส่วนที่ชาญฉลาดของระบบเข้ารหัสคีย์สาธารณะคือการออกแบบความสัมพันธ์ระหว่างสองคีย์

แผนการเข้ารหัสคีย์สาธารณะมีสามประเภท เราจะพูดถึงพวกเขาในส่วนต่อไปนี้ -

RSA Cryptosystem

ระบบเข้ารหัสนี้เป็นระบบเริ่มต้นระบบหนึ่ง ยังคงเป็นระบบเข้ารหัสที่มีการใช้งานมากที่สุดจนถึงทุกวันนี้ ระบบนี้คิดค้นโดยนักวิชาการสามคนRon Rivest, Adi Shamir, และ Len Adleman และด้วยเหตุนี้จึงเรียกว่า RSA cryptosystem

เราจะเห็นสองแง่มุมของ RSA cryptosystem การสร้างคู่คีย์ประการแรกและอัลกอริธึมการถอดรหัสการเข้ารหัสที่สอง

การสร้างคู่คีย์ RSA

แต่ละคนหรือฝ่ายที่ต้องการมีส่วนร่วมในการสื่อสารโดยใช้การเข้ารหัสจำเป็นต้องสร้างคีย์คู่หนึ่ง ได้แก่ คีย์สาธารณะและคีย์ส่วนตัว กระบวนการที่ตามมาในการสร้างคีย์อธิบายไว้ด้านล่าง -

Generate the RSA modulus (n)
- เลือกสองช่วงเวลาขนาดใหญ่ p และ q
- คำนวณ n = p * q สำหรับการเข้ารหัสที่แข็งแกร่งแบบไม่แตกหักให้ n เป็นจำนวนมากโดยทั่วไปต้องมีอย่างน้อย 512 บิต
Find Derived Number (e)
- จำนวน e ต้องมากกว่า 1 และน้อยกว่า (p - 1) (q - 1)
- ต้องไม่มีปัจจัยร่วมสำหรับ e และ (p - 1) (q - 1) ยกเว้น 1 ในคำอื่น ๆ สองตัวเลข e และ (p - 1) (q - 1) เป็น coprime
Form the public key
- คู่ของตัวเลข (n, e) สร้างคีย์สาธารณะ RSA และเปิดเผยต่อสาธารณะ
- สิ่งที่น่าสนใจคือแม้ว่า n จะเป็นส่วนหนึ่งของคีย์สาธารณะ แต่ความยากลำบากในการแยกตัวประกอบจำนวนเฉพาะจำนวนมากทำให้มั่นใจได้ว่าผู้โจมตีไม่สามารถค้นหาได้ในเวลา จำกัด ที่สอง primes (p & q) ที่ใช้เพื่อรับ n นี่คือจุดแข็งของ RSA
Generate the private key
- คีย์ส่วนตัว d คำนวณจาก p, q และ e สำหรับ n และ e ที่กำหนดจะมีหมายเลขเฉพาะ d
- ตัวเลข d คือค่าผกผันของ e modulo (p - 1) (q - 1) ซึ่งหมายความว่า d เป็นจำนวนที่น้อยกว่า (p - 1) (q - 1) ซึ่งเมื่อคูณด้วย e จะเท่ากับ 1 โมดูโล (p - 1) (q - 1)
- ความสัมพันธ์นี้เขียนในเชิงคณิตศาสตร์ดังนี้ -

ed = 1 mod (p − 1)(q − 1)

อัลกอริทึมแบบยุคลิดแบบขยายใช้ p, q และ e เป็นอินพุตและให้ d เป็นเอาต์พุต

ตัวอย่าง

ตัวอย่างการสร้างคู่คีย์ RSA แสดงไว้ด้านล่าง (เพื่อความง่ายในการทำความเข้าใจ primes p & q ที่นำมานี้เป็นค่าเล็กน้อยในทางปฏิบัติแล้วค่าเหล่านี้สูงมาก)

ให้สองไพรม์คือ p = 7 และ q = 13 ดังนั้นโมดูลัส n = pq = 7 x 13 = 91
เลือก e = 5 ซึ่งเป็นตัวเลือกที่ถูกต้องเนื่องจากไม่มีตัวเลขที่เป็นปัจจัยร่วมของ 5 และ (p - 1) (q - 1) = 6 × 12 = 72 ยกเว้น 1
คู่ของตัวเลข (n, e) = (91, 5) เป็นกุญแจสาธารณะและสามารถให้ใครก็ได้ที่เราต้องการให้สามารถส่งข้อความเข้ารหัสถึงเราได้
อินพุต p = 7, q = 13 และ e = 5 ไปยังอัลกอริทึมแบบยุคลิดขยาย ผลลัพธ์จะเป็น d = 29
ตรวจสอบว่า d ที่คำนวณถูกต้องโดยการคำนวณ -

de = 29 × 5 = 145 = 1 mod 72

ดังนั้นคีย์สาธารณะคือ (91, 5) และคีย์ส่วนตัวคือ (91, 29)

การเข้ารหัสและการถอดรหัส

เมื่อสร้างคู่คีย์แล้วกระบวนการเข้ารหัสและถอดรหัสจะค่อนข้างตรงไปตรงมาและง่ายต่อการคำนวณ

ที่น่าสนใจคือ RSA ไม่ได้ทำงานโดยตรงกับสตริงของบิตเช่นเดียวกับการเข้ารหัสคีย์สมมาตร ทำงานกับตัวเลข modulo n ดังนั้นจึงจำเป็นต้องแสดงข้อความธรรมดาเป็นชุดของตัวเลขที่น้อยกว่า n

การเข้ารหัส RSA

สมมติว่าผู้ส่งต้องการส่งข้อความถึงคนที่มีคีย์สาธารณะคือ (n, e)
จากนั้นผู้ส่งจะแสดงข้อความธรรมดาเป็นชุดของตัวเลขที่น้อยกว่า n
ในการเข้ารหัสข้อความธรรมดา P ตัวแรกซึ่งเป็นตัวเลขโมดูโล n กระบวนการเข้ารหัสเป็นขั้นตอนทางคณิตศาสตร์ง่ายๆเช่น -

C = P^e mod n

กล่าวอีกนัยหนึ่งไซเฟอร์เท็กซ์ C เท่ากับข้อความธรรมดา P คูณด้วยตัวมันเอง e คูณแล้วลดโมดูโล n ซึ่งหมายความว่า C เป็นตัวเลขที่น้อยกว่า n ด้วย
กลับไปที่ตัวอย่างการสร้างคีย์ของเราด้วยข้อความธรรมดา P = 10 เราจะได้รับการเข้ารหัส C -

C = 10⁵ mod 91

การถอดรหัส RSA

กระบวนการถอดรหัสสำหรับ RSA นั้นตรงไปตรงมามากเช่นกัน สมมติว่าผู้รับของ public-key pair (n, e) ได้รับ ciphertext C
ตัวรับยก C ให้เป็นพลังของคีย์ส่วนตัว d โมดูโล n ผลลัพธ์จะเป็นข้อความธรรมดา P

Plaintext = C^d mod n

กลับไปที่ตัวอย่างตัวเลขของเราอีกครั้งการเข้ารหัส C = 82 จะถูกถอดรหัสเป็นหมายเลข 10 โดยใช้คีย์ส่วนตัว 29 -

Plaintext = 82²⁹ mod 91 = 10

การวิเคราะห์ RSA

ความปลอดภัยของ RSA ขึ้นอยู่กับจุดแข็งของสองฟังก์ชันที่แยกจากกัน RSA cryptosystem เป็นจุดแข็งของระบบเข้ารหัสคีย์สาธารณะที่ได้รับความนิยมมากที่สุดซึ่งขึ้นอยู่กับความยากลำบากในทางปฏิบัติในการแยกตัวเลขจำนวนมาก

Encryption Function - ถือเป็นฟังก์ชันทางเดียวในการแปลงข้อความธรรมดาเป็นไซเฟอร์เท็กซ์และสามารถย้อนกลับได้เฉพาะเมื่อมีความรู้เกี่ยวกับคีย์ส่วนตัว d
Key Generation- ความยากในการกำหนดคีย์ส่วนตัวจากคีย์สาธารณะ RSA นั้นเทียบเท่ากับการแยกตัวประกอบโมดูลัส n ดังนั้นผู้โจมตีจึงไม่สามารถใช้ความรู้เกี่ยวกับคีย์สาธารณะ RSA เพื่อกำหนดคีย์ส่วนตัวของ RSA ได้เว้นแต่เขาจะแยกตัวประกอบ n ได้ นอกจากนี้ยังเป็นฟังก์ชันทางเดียวการเปลี่ยนจากค่า p & q ไปเป็นโมดูลัส n นั้นง่าย แต่ไม่สามารถย้อนกลับได้

หากฟังก์ชันทั้งสองนี้พิสูจน์แล้วว่าไม่ใช่ทางเดียว RSA ก็จะเสีย ในความเป็นจริงหากมีการพัฒนาเทคนิคการแยกตัวประกอบอย่างมีประสิทธิภาพแล้ว RSA ก็จะไม่ปลอดภัยอีกต่อไป

ความแข็งแกร่งของการเข้ารหัส RSA ลดลงอย่างมากในการต่อต้านการโจมตีหากหมายเลข p และ q ไม่ใช่จำนวนครั้งใหญ่และ / หรือคีย์สาธารณะที่เลือก e เป็นตัวเลขที่น้อย

ElGamal Cryptosystem

นอกจาก RSA แล้วยังมีระบบเข้ารหัสคีย์สาธารณะอื่น ๆ ที่เสนอ หลายคนอ้างอิงจากปัญหาลอการิทึมแบบไม่ต่อเนื่องในเวอร์ชันต่างๆ

ElGamal cryptosystem เรียกว่า Elliptic Curve Variant มีพื้นฐานมาจากปัญหาลอการิทึมแบบไม่ต่อเนื่อง ได้รับความแข็งแกร่งจากสมมติฐานที่ว่าไม่พบลอการิทึมแบบไม่ต่อเนื่องในกรอบเวลาที่ใช้งานได้จริงสำหรับจำนวนที่กำหนดในขณะที่การดำเนินการผกผันของกำลังสามารถคำนวณได้อย่างมีประสิทธิภาพ

ให้เราดู ElGamal เวอร์ชันง่ายๆที่ใช้งานได้กับตัวเลข modulo p ในกรณีของรูปแบบของเส้นโค้งรูปไข่จะขึ้นอยู่กับระบบตัวเลขที่แตกต่างกันมาก

การสร้างคู่คีย์ ElGamal

ผู้ใช้ ElGamal cryptosystem แต่ละคนจะสร้างคู่คีย์ผ่านดังนี้ -

Choosing a large prime p. โดยทั่วไปจะเลือกจำนวนเฉพาะที่มีความยาว 1024 ถึง 2048 บิต
Choosing a generator element g.
- ตัวเลขนี้ต้องอยู่ระหว่าง 1 ถึง p - 1 แต่ต้องไม่เป็นตัวเลขใด ๆ
- มันเป็นเครื่องกำเนิดของกลุ่มจำนวนเต็มแบบทวีคูณโมดูโลพี ซึ่งหมายความว่าสำหรับทุกจำนวนเต็ม m co-prime ถึง p จะมีจำนวนเต็ม k เช่นนั้น g ^k = a mod n
  
  ตัวอย่างเช่น 3 คือตัวสร้างของกลุ่ม 5 (Z ₅ = {1, 2, 3, 4})

น	3 ⁿ	3 ⁿ mod 5
1	3	3
2	9	4
3	27	2
4	81	1

Choosing the private key. คีย์ส่วนตัว x คือตัวเลขใด ๆ ที่ใหญ่กว่า 1 และเล็กกว่า p − 1
Computing part of the public key. ค่า y คำนวณจากพารามิเตอร์ p, g และคีย์ส่วนตัว x ดังนี้ -

y = g^x mod p

Obtaining Public key. คีย์สาธารณะ ElGamal ประกอบด้วยพารามิเตอร์สามตัว (p, g, y)

ตัวอย่างเช่นสมมติว่า p = 17 และ g = 6 (ยืนยันได้ว่า 6 เป็นตัวกำเนิดของกลุ่ม Z ₁₇ ) คีย์ส่วนตัว x สามารถเป็นตัวเลขใดก็ได้ที่ใหญ่กว่า 1 และเล็กกว่า 71 ดังนั้นเราจึงเลือก x = 5 จากนั้นค่า y จะถูกคำนวณดังนี้ -

y = 6⁵ mod 17 = 7

ดังนั้นคีย์ส่วนตัวคือ 62 และคีย์สาธารณะคือ (17, 6, 7)

การเข้ารหัสและการถอดรหัส

การสร้างคู่คีย์ ElGamal ค่อนข้างง่ายกว่ากระบวนการเทียบเท่าสำหรับ RSA แต่การเข้ารหัสและถอดรหัสนั้นซับซ้อนกว่า RSA เล็กน้อย

การเข้ารหัส ElGamal

สมมติว่าผู้ส่งต้องการส่งข้อความธรรมดาถึงคนที่มีคีย์สาธารณะ ElGamal คือ (p, g, y) แล้ว -

ผู้ส่งแทนข้อความธรรมดาเป็นอนุกรมของตัวเลขโมดูโลพี
ในการเข้ารหัสข้อความธรรมดา P ตัวแรกซึ่งแสดงเป็นตัวเลขโมดูโล p กระบวนการเข้ารหัสเพื่อรับ ciphertext C มีดังต่อไปนี้ -
- สุ่มสร้างตัวเลข k;
- คำนวณสองค่า C1 และ C2 โดยที่ -

C1 = g^k mod p
C2 = (P^*y^k) mod p

ส่ง ciphertext C ซึ่งประกอบด้วยสองค่าที่แยกจากกัน (C1, C2) ส่งถึงกัน
อ้างอิงถึงตัวอย่างการสร้างคีย์ ElGamal ที่ให้ไว้ข้างต้นข้อความธรรมดา P = 13 จะถูกเข้ารหัสดังนี้ -
- สร้างตัวเลขแบบสุ่มพูดว่า k = 10
- คำนวณค่าสองค่า C1 และ C2 โดยที่ -

C1 = 6¹⁰ mod 17
C2 = (13^*7¹⁰) mod 17 = 9

ส่ง ciphertext C = (C1, C2) = (15, 9)

การถอดรหัส ElGamal

ในการถอดรหัสรหัสลับ (C1, C2) โดยใช้คีย์ส่วนตัว x ให้ดำเนินการสองขั้นตอนต่อไปนี้ -
- คำนวณค่าผกผันโมดูลาร์ของ (C1) ^xโมดูโล p ซึ่งก็คือ (C1) ^-xโดยทั่วไปเรียกว่าปัจจัยการถอดรหัส
- รับข้อความธรรมดาโดยใช้สูตรต่อไปนี้ -

C2 × (C1)^-x mod p = Plaintext

ในตัวอย่างของเราในการถอดรหัสรหัสลับ C = (C1, C2) = (15, 9) โดยใช้คีย์ส่วนตัว x = 5 ปัจจัยการถอดรหัสคือ

15^-5 mod 17 = 9

แยกข้อความธรรมดา P = (9 × 9) mod 17 = 13

การวิเคราะห์ ElGamal

ในระบบ ElGamal ผู้ใช้แต่ละคนมีคีย์ส่วนตัว x และมีthree components ของคีย์สาธารณะ - prime modulus p, generator g, and public Y = g^x mod p. จุดแข็งของ ElGamal ขึ้นอยู่กับความยากของปัญหาลอการิทึมแบบไม่ต่อเนื่อง

ขนาดคีย์ที่ปลอดภัยโดยทั่วไปคือ> 1024 บิต ทุกวันนี้ยังใช้คีย์แบบยาว 2048 บิต ในส่วนหน้าความเร็วในการประมวลผล Elgamal ค่อนข้างช้าซึ่งส่วนใหญ่ใช้สำหรับโปรโตคอลการตรวจสอบสิทธิ์ที่สำคัญ เนื่องจากประสิทธิภาพในการประมวลผลที่สูงขึ้นรูปแบบ Elliptic Curve ของ ElGamal จึงได้รับความนิยมมากขึ้นเรื่อย ๆ

การเข้ารหัส Elliptic Curve (ECC)

Elliptic Curve Cryptography (ECC) เป็นคำที่ใช้อธิบายชุดเครื่องมือและโปรโตคอลการเข้ารหัสที่มีการรักษาความปลอดภัยตามเวอร์ชันพิเศษของปัญหาลอการิทึมแบบไม่ต่อเนื่อง ไม่ใช้ตัวเลขโมดูโลพี

ECC ขึ้นอยู่กับชุดของตัวเลขที่เกี่ยวข้องกับวัตถุทางคณิตศาสตร์ที่เรียกว่าเส้นโค้งวงรี มีกฎสำหรับการเพิ่มและคำนวณทวีคูณของตัวเลขเหล่านี้เช่นเดียวกับที่มีสำหรับตัวเลขโมดูโลพี

ECC ประกอบด้วยรูปแบบของรูปแบบการเข้ารหัสจำนวนมากที่ได้รับการออกแบบมาสำหรับหมายเลขแบบแยกส่วนเช่นการเข้ารหัส ElGamal และอัลกอริทึมลายเซ็นดิจิทัล

เชื่อกันว่าปัญหาลอการิทึมแบบไม่ต่อเนื่องนั้นยากกว่ามากเมื่อนำไปใช้กับจุดบนเส้นโค้งวงรี สิ่งนี้แจ้งให้เปลี่ยนจากตัวเลขโมดูโล p เป็นจุดบนเส้นโค้งวงรี นอกจากนี้ยังสามารถรับระดับการรักษาความปลอดภัยที่เทียบเท่าได้ด้วยคีย์ที่สั้นกว่าหากเราใช้ตัวแปรตามเส้นโค้งรูปไข่

คีย์ที่สั้นกว่าส่งผลให้เกิดประโยชน์สองประการ -

ง่ายต่อการจัดการที่สำคัญ
การคำนวณที่มีประสิทธิภาพ

ประโยชน์เหล่านี้ทำให้รูปแบบการเข้ารหัสรูปไข่โค้งตามรูปแบบที่น่าสนใจอย่างมากสำหรับแอปพลิเคชันที่ทรัพยากรคอมพิวเตอร์มีข้อ จำกัด

RSA และ ElGamal Schemes - การเปรียบเทียบ

ให้เราเปรียบเทียบโครงร่าง RSA และ ElGamal สั้น ๆ ในแง่มุมต่างๆ

RSA	ElGamal
มีประสิทธิภาพมากขึ้นสำหรับการเข้ารหัส	มีประสิทธิภาพมากขึ้นสำหรับการถอดรหัส
มีประสิทธิภาพน้อยกว่าสำหรับการถอดรหัส	มีประสิทธิภาพมากขึ้นสำหรับการถอดรหัส
สำหรับระดับความปลอดภัยเฉพาะต้องใช้คีย์ยาวใน RSA	เพื่อความปลอดภัยในระดับเดียวกันจำเป็นต้องใช้คีย์ที่สั้นมาก
เป็นที่ยอมรับและใช้กันอย่างแพร่หลาย	เป็นสินค้าใหม่และไม่เป็นที่นิยมในตลาด