ฟังก์ชั่นพิเศษของ LPF และ HPF
วงจรกรองความถี่ต่ำและความถี่สูงใช้เป็นวงจรพิเศษในการใช้งานหลายประเภท Low-pass filter (LPF) สามารถทำงานเป็นไฟล์Integratorในขณะที่ตัวกรองความถี่สูง (HPF) สามารถทำงานเป็นไฟล์ Differentiator. ฟังก์ชันทางคณิตศาสตร์ทั้งสองนี้เป็นไปได้เฉพาะกับวงจรเหล่านี้ซึ่งลดความพยายามของวิศวกรอิเล็กทรอนิกส์ในหลาย ๆ แอปพลิเคชัน
ตัวกรองความถี่ต่ำเป็นตัวรวม
ที่ความถี่ต่ำรีแอคแตนซ์ความจุมีแนวโน้มที่จะไม่สิ้นสุดและที่ความถี่สูงรีแอคแตนซ์จะกลายเป็นศูนย์ ดังนั้นที่ความถี่ต่ำ LPF จึงมีเอาต์พุตที่ จำกัด และที่ความถี่สูงเอาต์พุตจะเป็นศูนย์ซึ่งเหมือนกับวงจรอินทิเกรเตอร์ ดังนั้นตัวกรองความถี่ต่ำจึงสามารถกล่าวได้ว่าทำงานเป็นไฟล์integrator.
เพื่อให้ LPF ทำงานเป็นตัวรวม
$$ \ tau \ gg T $$
โดยที่ $ \ tau = RC $ คือค่าคงที่เวลาของวงจร
จากนั้นการแปรผันของแรงดันไฟฟ้าใน C จะน้อยมาก
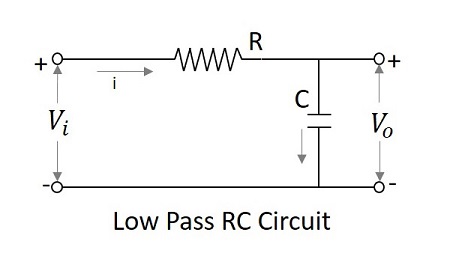
$$ V_ {i} = iR + \ frac {1} {C} \ int i \: dt $$
$$ V_ {i} \ Cong iR $$
$$ ตั้งแต่ \: \: \ frac {1} {C} \ int i \: dt \ ll iR $$
$$ i = \ frac {V_ {i}} {R} $$
$$ ตั้งแต่ \: \: V_ {0} = \ frac {1} {C} \ int i dt = \ frac {1} {RC} \ int V_ {i} dt = \ frac {1} {\ tau} \ int V_ {i} dt $$
$$ Output \ propto \ int อินพุต $$
ดังนั้น LPF ที่มีค่าคงที่ของเวลามากจึงสร้างเอาต์พุตที่เป็นสัดส่วนกับอินทิกรัลของอินพุต
การตอบสนองต่อความถี่
การตอบสนองต่อความถี่ของตัวกรองความถี่ต่ำที่ใช้งานได้จริงเมื่อทำงานเป็นตัวรวมมีดังที่แสดงด้านล่าง
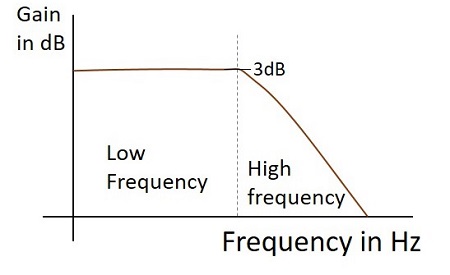
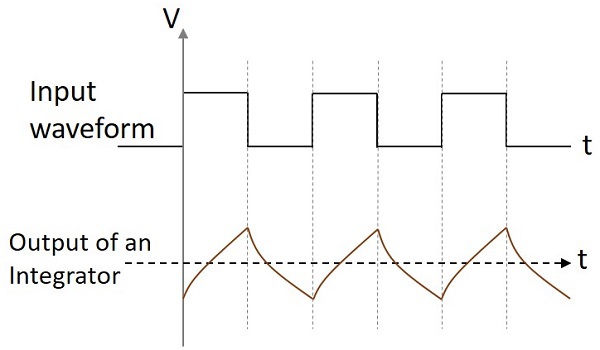
รูปคลื่นเอาต์พุต
ถ้าวงจรอินทิเกรเตอร์ได้รับอินพุตไซน์เวฟเอาต์พุตจะเป็นคลื่นโคไซน์ หากอินพุตเป็นคลื่นสี่เหลี่ยมรูปคลื่นเอาท์พุตจะเปลี่ยนรูปร่างและปรากฏดังรูปด้านล่าง
ตัวกรองความถี่สูงเป็นตัวแยกความแตกต่าง
ที่ความถี่ต่ำเอาต์พุตของตัวแยกความแตกต่างจะเป็นศูนย์ในขณะที่ความถี่สูงเอาต์พุตจะมีค่า จำกัด สิ่งนี้เหมือนกับการสร้างความแตกต่าง ดังนั้นตัวกรองความถี่สูงจึงถูกกล่าวว่าเป็นตัวกรองที่แตกต่าง
หากค่าคงที่ของ RC HPF มีค่าน้อยกว่าช่วงเวลาของสัญญาณอินพุตมากวงจรจะทำงานเป็นตัวสร้างความแตกต่าง จากนั้นแรงดันตกคร่อม R มีค่าน้อยมากเมื่อเทียบกับการตกคร่อม C
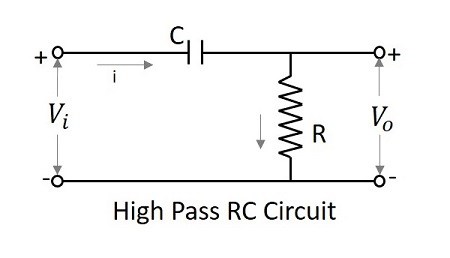
$$ V_ {i} = \ frac {1} {C} \ int i \: dt + iR $$
แต่ $ iR = V_ {0} $ มีขนาดเล็ก
$$ ตั้งแต่ V_ {i} = \ frac {1} {C} \ int i \: dt $$
$$ i = \ frac {V_ {0}} {R} $$
$$ ตั้งแต่ \: V_ {i} = \ frac {1} {\ tau} \ int V_ {0} \: dt $$
โดยที่ $ \ tau = RC $ คือค่าคงที่เวลาของวงจร
ความแตกต่างทั้งสองด้าน
$$ \ frac {dV_ {i}} {dt} = \ frac {V_0} {\ tau} $$
$$ V_ {0} = \ tau \ frac {dV_ {i}} {dt} $$
$$ ตั้งแต่ \: V_ {0} \ propto \ frac {dV_ {i}} {dt} $$
เอาต์พุตเป็นสัดส่วนกับความแตกต่างของสัญญาณอินพุต
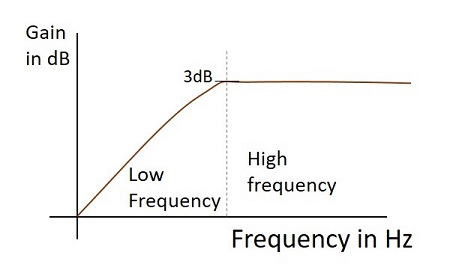
การตอบสนองต่อความถี่
การตอบสนองความถี่ของตัวกรองความถี่สูงที่ใช้งานได้จริงเมื่อทำงานเป็นตัวแยกความแตกต่างจะเป็นดังที่แสดงด้านล่าง
รูปคลื่นเอาท์พุท
ถ้าวงจรดิฟเฟอเรนเอเตอร์ได้รับอินพุตไซน์เวฟเอาต์พุตจะเป็นคลื่นโคไซน์ หากอินพุตเป็นคลื่นสี่เหลี่ยมรูปคลื่นเอาท์พุตจะเปลี่ยนรูปร่างและปรากฏดังรูปด้านล่าง
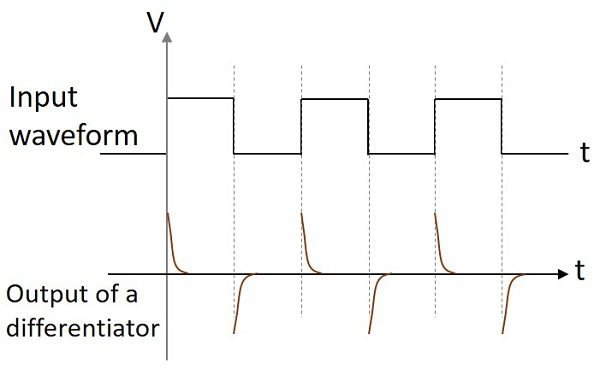
วงจรทั้งสองนี้ส่วนใหญ่ใช้ในงานอิเล็กทรอนิกส์ต่างๆ วงจรที่แตกต่างจะสร้างแรงดันเอาต์พุตคงที่เมื่ออินพุตที่ใช้มีแนวโน้มที่จะเปลี่ยนไปเรื่อย ๆ วงจรอินทิเกรเตอร์จะสร้างแรงดันเอาต์พุตที่เปลี่ยนแปลงไปเรื่อย ๆ เมื่อแรงดันไฟฟ้าขาเข้าที่ใช้คงที่