การสร้างแบบจำลองและการจำลอง - คู่มือฉบับย่อ

Modellingเป็นขั้นตอนการแสดงแบบจำลองซึ่งรวมถึงการก่อสร้างและการทำงาน แบบจำลองนี้คล้ายกับระบบจริงซึ่งช่วยให้นักวิเคราะห์คาดการณ์ผลกระทบของการเปลี่ยนแปลงในระบบ กล่าวอีกนัยหนึ่งการสร้างแบบจำลองคือการสร้างแบบจำลองซึ่งแสดงถึงระบบรวมทั้งคุณสมบัติของมัน เป็นการสร้างแบบจำลอง

Simulationของระบบคือการทำงานของโมเดลในแง่ของเวลาหรือพื้นที่ซึ่งช่วยวิเคราะห์ประสิทธิภาพของระบบที่มีอยู่หรือระบบที่เสนอ กล่าวอีกนัยหนึ่งการจำลองเป็นกระบวนการของการใช้แบบจำลองเพื่อศึกษาประสิทธิภาพของระบบ เป็นการกระทำโดยใช้ตัวแบบจำลอง

ประวัติศาสตร์การจำลองสถานการณ์

มุมมองทางประวัติศาสตร์ของการจำลองจะแจกแจงตามลำดับเวลา

• 1940 - วิธีการที่ชื่อว่า 'Monte Carlo' ได้รับการพัฒนาโดยนักวิจัย (John von Neumann, Stanislaw Ulan, Edward Teller, Herman Kahn) และนักฟิสิกส์ที่ทำงานในโครงการแมนฮัตตันเพื่อศึกษาการกระเจิงของนิวตรอน

• 1960 - ภาษาจำลองวัตถุประสงค์พิเศษแรกได้รับการพัฒนาเช่น SIMSCRIPT โดย Harry Markowitz ที่ RAND Corporation

• 1970 - ในช่วงเวลานี้ได้เริ่มการวิจัยเกี่ยวกับพื้นฐานทางคณิตศาสตร์ของการจำลอง

• 1980 - ในช่วงเวลานี้มีการพัฒนาซอฟต์แวร์จำลองบนพีซีอินเทอร์เฟซผู้ใช้แบบกราฟิกและการเขียนโปรแกรมเชิงวัตถุ

• 1990 - ในช่วงเวลานี้ได้มีการพัฒนาการจำลองบนเว็บกราฟิกเคลื่อนไหวแฟนซีการเพิ่มประสิทธิภาพตามการจำลองวิธีการมอนติคาร์โลของ Markov-chain ได้รับการพัฒนา

การพัฒนาโมเดลจำลอง

โมเดลจำลองประกอบด้วยองค์ประกอบต่อไปนี้เอนทิตีระบบตัวแปรอินพุตการวัดประสิทธิภาพและความสัมพันธ์เชิงฟังก์ชัน ต่อไปนี้เป็นขั้นตอนในการพัฒนาแบบจำลอง

• Step 1 - ระบุปัญหากับระบบที่มีอยู่หรือตั้งข้อกำหนดของระบบที่เสนอ

• Step 2 - ออกแบบปัญหาพร้อมกับดูแลปัจจัยและข้อ จำกัด ของระบบที่มีอยู่

• Step 3 - รวบรวมและเริ่มประมวลผลข้อมูลระบบสังเกตประสิทธิภาพและผลลัพธ์

• Step 4 - พัฒนาแบบจำลองโดยใช้แผนภาพเครือข่ายและตรวจสอบโดยใช้เทคนิคการตรวจสอบต่างๆ

• Step 5 - ตรวจสอบโมเดลโดยเปรียบเทียบประสิทธิภาพภายใต้เงื่อนไขต่างๆกับระบบจริง

• Step 6 - สร้างเอกสารของแบบจำลองสำหรับการใช้งานในอนาคตซึ่งรวมถึงวัตถุประสงค์สมมติฐานตัวแปรอินพุตและรายละเอียดประสิทธิภาพ

• Step 7 - เลือกการออกแบบการทดลองที่เหมาะสมตามความต้องการ

• Step 8 - กำหนดเงื่อนไขการทดลองในแบบจำลองและสังเกตผลลัพธ์

ทำการวิเคราะห์การจำลอง

ต่อไปนี้เป็นขั้นตอนในการวิเคราะห์การจำลอง

• Step 1 - เตรียมคำชี้แจงปัญหา

• Step 2- เลือกตัวแปรอินพุตและสร้างเอนทิตีสำหรับกระบวนการจำลอง ตัวแปรมีสองประเภท - ตัวแปรการตัดสินใจและตัวแปรที่ควบคุมไม่ได้ ตัวแปรการตัดสินใจถูกควบคุมโดยโปรแกรมเมอร์ในขณะที่ตัวแปรที่ไม่สามารถควบคุมได้คือตัวแปรสุ่ม

• Step 3 - สร้างข้อ จำกัด เกี่ยวกับตัวแปรการตัดสินใจโดยกำหนดให้กับกระบวนการจำลอง

• Step 4 - กำหนดตัวแปรผลลัพธ์

• Step 5 - รวบรวมข้อมูลจากระบบในชีวิตจริงเพื่อป้อนลงในการจำลอง

• Step 6 - พัฒนาผังงานแสดงความคืบหน้าของกระบวนการจำลอง

• Step 7 - เลือกซอฟต์แวร์จำลองที่เหมาะสมเพื่อเรียกใช้โมเดล

• Step 8 - ตรวจสอบโมเดลจำลองโดยเปรียบเทียบผลลัพธ์กับระบบเรียลไทม์

• Step 9 - ทำการทดลองเกี่ยวกับแบบจำลองโดยการเปลี่ยนค่าตัวแปรเพื่อหาทางออกที่ดีที่สุด

• Step 10 - สุดท้ายใช้ผลลัพธ์เหล่านี้ในระบบเรียลไทม์

การสร้างแบบจำลองและการจำลอง─ข้อดี

ต่อไปนี้เป็นข้อดีของการใช้ Modeling and Simulation -

• Easy to understand - ช่วยให้เข้าใจว่าระบบทำงานอย่างไรโดยไม่ต้องทำงานบนระบบเรียลไทม์

• Easy to test - อนุญาตให้ทำการเปลี่ยนแปลงในระบบและผลกระทบต่อเอาต์พุตโดยไม่ต้องทำงานกับระบบเรียลไทม์

• Easy to upgrade - อนุญาตให้กำหนดความต้องการของระบบโดยใช้การกำหนดค่าต่างๆ

• Easy to identifying constraints - อนุญาตให้ทำการวิเคราะห์คอขวดที่ทำให้กระบวนการทำงานข้อมูล ฯลฯ ล่าช้า

• Easy to diagnose problems- ระบบบางระบบมีความซับซ้อนมากจนไม่ง่ายที่จะเข้าใจการโต้ตอบในแต่ละครั้ง อย่างไรก็ตามการสร้างแบบจำลองและการจำลองช่วยให้เข้าใจการโต้ตอบทั้งหมดและวิเคราะห์ผลกระทบ นอกจากนี้ยังสามารถสำรวจนโยบายการดำเนินงานและขั้นตอนใหม่ ๆ ได้โดยไม่ส่งผลกระทบต่อระบบจริง

การสร้างแบบจำลองและการจำลองสถานการณ์─ข้อเสีย

ต่อไปนี้เป็นข้อเสียของการใช้ Modeling and Simulation -

• การออกแบบโมเดลเป็นศิลปะที่ต้องอาศัยความรู้การฝึกอบรมและประสบการณ์

• การดำเนินการจะดำเนินการในระบบโดยใช้หมายเลขสุ่มดังนั้นจึงยากที่จะคาดเดาผลลัพธ์

• การจำลองสถานการณ์ต้องใช้กำลังคนและเป็นกระบวนการที่ใช้เวลานาน

• ผลการจำลองเป็นเรื่องยากที่จะแปล ต้องใช้ผู้เชี่ยวชาญในการทำความเข้าใจ

• กระบวนการจำลองมีราคาแพง

การสร้างแบบจำลองและการจำลอง─พื้นที่การใช้งาน

การสร้างแบบจำลองและการจำลองสามารถนำไปใช้กับพื้นที่ต่อไปนี้ - การใช้งานทางทหารการฝึกอบรมและการสนับสนุนการออกแบบเซมิคอนดักเตอร์โทรคมนาคมการออกแบบและการนำเสนอทางวิศวกรรมโยธาและแบบจำลองทางธุรกิจอิเล็กทรอนิกส์

นอกจากนี้ยังใช้เพื่อศึกษาโครงสร้างภายในของระบบที่ซับซ้อนเช่นระบบชีวภาพ ใช้ในขณะที่ปรับการออกแบบระบบให้เหมาะสมเช่นอัลกอริทึมการกำหนดเส้นทางสายการประกอบ ฯลฯ ใช้เพื่อทดสอบการออกแบบและนโยบายใหม่ ๆ ใช้เพื่อตรวจสอบโซลูชันการวิเคราะห์

ในบทนี้เราจะพูดถึงแนวคิดต่างๆและการแบ่งประเภทของการสร้างแบบจำลอง

โมเดลและกิจกรรม

ต่อไปนี้เป็นแนวคิดพื้นฐานของการสร้างแบบจำลองและการจำลอง

• Object เป็นหน่วยงานที่มีอยู่ในโลกแห่งความเป็นจริงเพื่อศึกษาพฤติกรรมของแบบจำลอง

• Base Model เป็นคำอธิบายเชิงสมมุติเกี่ยวกับคุณสมบัติของวัตถุและพฤติกรรมของวัตถุซึ่งใช้ได้กับแบบจำลอง

• System เป็นวัตถุที่เปล่งออกมาภายใต้เงื่อนไขที่แน่นอนซึ่งมีอยู่ในโลกแห่งความเป็นจริง

• Experimental Frameใช้เพื่อศึกษาระบบในโลกแห่งความเป็นจริงเช่นเงื่อนไขการทดลองแง่มุมวัตถุประสงค์ ฯลฯ Basic Experimental Frame ประกอบด้วยตัวแปรสองชุด ได้แก่ ตัวแปรอินพุตเฟรมและตัวแปรเฟรมเอาต์พุตซึ่งตรงกับเทอร์มินัลของระบบหรือโมเดล ตัวแปรอินพุตเฟรมมีหน้าที่ในการจับคู่อินพุตที่ใช้กับระบบหรือโมเดล ตัวแปรเฟรมเอาต์พุตมีหน้าที่ในการจับคู่ค่าเอาต์พุตกับระบบหรือโมเดล

• Lumped Model คือคำอธิบายที่แน่นอนของระบบซึ่งเป็นไปตามเงื่อนไขที่ระบุของ Experimental Frame ที่กำหนด

• Verificationเป็นกระบวนการเปรียบเทียบสองรายการขึ้นไปเพื่อให้แน่ใจว่าถูกต้อง ในการสร้างแบบจำลองและการจำลองสถานการณ์การตรวจสอบสามารถทำได้โดยการเปรียบเทียบความสอดคล้องของโปรแกรมจำลองและแบบจำลองแบบรวมเพื่อให้แน่ใจว่ามีประสิทธิภาพ มีหลายวิธีในการดำเนินการตรวจสอบความถูกต้องซึ่งเราจะกล่าวถึงในบทที่แยกต่างหาก

• Validationเป็นกระบวนการเปรียบเทียบผลลัพธ์สองรายการ ในการสร้างแบบจำลองและการจำลองสถานการณ์การตรวจสอบจะดำเนินการโดยการเปรียบเทียบการวัดการทดลองกับผลการจำลองภายในบริบทของกรอบการทดลอง โมเดลไม่ถูกต้องหากผลลัพธ์ไม่ตรงกัน มีหลายวิธีในการดำเนินการตรวจสอบความถูกต้องซึ่งเราจะกล่าวถึงในแต่ละบท

ตัวแปรสถานะของระบบ

ตัวแปรสถานะระบบคือชุดข้อมูลที่จำเป็นในการกำหนดกระบวนการภายในระบบ ณ ช่วงเวลาที่กำหนด

• ใน discrete-event modelตัวแปรสถานะของระบบจะคงที่ตลอดช่วงเวลาและค่าจะเปลี่ยนไปตามจุดที่กำหนดซึ่งเรียกว่าเหตุการณ์ครั้ง

• ใน continuous-event modelตัวแปรสถานะของระบบถูกกำหนดโดยผลลัพธ์สมการเชิงอนุพันธ์ซึ่งค่าเปลี่ยนแปลงอย่างต่อเนื่องตลอดเวลา

ต่อไปนี้เป็นตัวแปรสถานะของระบบ -

• Entities & Attributes- เอนทิตีแสดงถึงออบเจ็กต์ที่มีค่าคงที่หรือไดนามิกขึ้นอยู่กับกระบวนการกับเอนทิตีอื่น แอตทริบิวต์คือค่าท้องถิ่นที่ใช้โดยเอนทิตี

• Resources- ทรัพยากรคือเอนทิตีที่ให้บริการแก่เอนทิตีแบบไดนามิกทีละหนึ่งรายการขึ้นไป เอนทิตีแบบไดนามิกสามารถร้องขอหนึ่งหน่วยหรือมากกว่าของทรัพยากร หากได้รับการยอมรับเอนทิตีสามารถใช้ทรัพยากรและปล่อยเมื่อเสร็จสมบูรณ์ หากถูกปฏิเสธเอนทิตีสามารถเข้าร่วมคิวได้

• Lists- รายการใช้เพื่อแสดงคิวที่ใช้โดยเอนทิตีและทรัพยากร มีความเป็นไปได้ต่างๆของคิวเช่น LIFO, FIFO เป็นต้นขึ้นอยู่กับกระบวนการ

• Delay - เป็นระยะเวลาไม่แน่นอนที่เกิดจากการรวมกันของเงื่อนไขของระบบ

การจำแนกประเภทของโมเดล

ระบบสามารถแบ่งออกเป็นประเภทต่างๆดังต่อไปนี้

• Discrete-Event Simulation Model- ในโมเดลนี้ค่าตัวแปรสถานะจะเปลี่ยนเฉพาะในบางจุดที่ไม่ต่อเนื่องในช่วงเวลาที่เหตุการณ์เกิดขึ้น กิจกรรมจะเกิดขึ้นตามเวลากิจกรรมที่กำหนดและความล่าช้าเท่านั้น

• Stochastic vs. Deterministic Systems - ระบบ Stochastic ไม่ได้รับผลกระทบจากการสุ่มและผลลัพธ์ของมันไม่ใช่ตัวแปรสุ่มในขณะที่ระบบดีเทอร์มินิสต์จะได้รับผลกระทบจากการสุ่มและผลลัพธ์ของมันเป็นตัวแปรสุ่ม

• Static vs. Dynamic Simulation- การจำลองแบบคงที่รวมถึงโมเดลที่ไม่ได้รับผลกระทบตามเวลา ตัวอย่างเช่น Monte Carlo Model Dynamic Simulation ประกอบด้วยโมเดลที่ได้รับผลกระทบตามเวลา

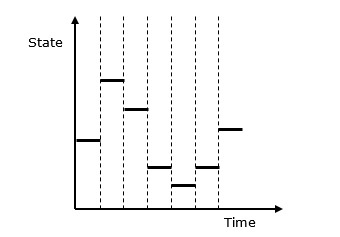
• Discrete vs. Continuous Systems- ระบบไม่ต่อเนื่องได้รับผลกระทบจากการเปลี่ยนแปลงตัวแปรของรัฐ ณ เวลาที่ไม่ต่อเนื่อง พฤติกรรมของมันถูกแสดงในการแสดงกราฟิกต่อไปนี้

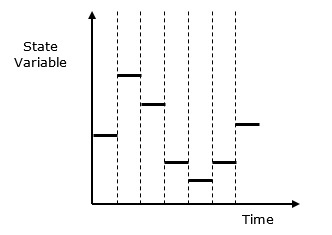
ระบบต่อเนื่องได้รับผลกระทบจากตัวแปรสถานะซึ่งเปลี่ยนไปเรื่อย ๆ ตามฟังก์ชันตามเวลา พฤติกรรมของมันถูกแสดงในการแสดงกราฟิกต่อไปนี้

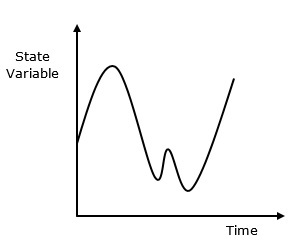
กระบวนการสร้างแบบจำลอง

กระบวนการสร้างแบบจำลองประกอบด้วยขั้นตอนต่อไปนี้

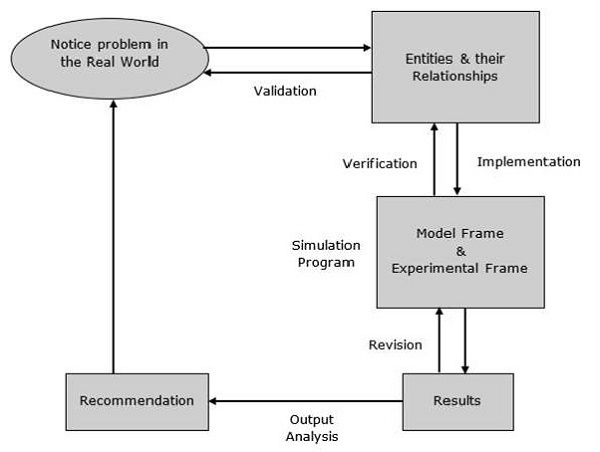
Step 1- ตรวจสอบปัญหา ในขั้นตอนนี้เราต้องเข้าใจปัญหาและเลือกการจัดประเภทตามลำดับเช่นกำหนดหรือสุ่ม

Step 2- ออกแบบโมเดล ในขั้นตอนนี้เราต้องดำเนินการง่ายๆดังต่อไปนี้ซึ่งช่วยให้เราออกแบบแบบจำลอง -

• รวบรวมข้อมูลตามลักษณะการทำงานของระบบและข้อกำหนดในอนาคต

• วิเคราะห์คุณลักษณะของระบบสมมติฐานและการดำเนินการที่จำเป็นเพื่อทำให้แบบจำลองประสบความสำเร็จ

• กำหนดชื่อตัวแปรฟังก์ชันหน่วยความสัมพันธ์และแอ็พพลิเคชันที่ใช้ในโมเดล

• แก้ไขแบบจำลองโดยใช้เทคนิคที่เหมาะสมและตรวจสอบผลลัพธ์โดยใช้วิธีการตรวจสอบ จากนั้นตรวจสอบผลลัพธ์

• จัดทำรายงานซึ่งประกอบด้วยผลลัพธ์การตีความข้อสรุปและข้อเสนอแนะ

Step 3- ให้คำแนะนำหลังจากเสร็จสิ้นกระบวนการทั้งหมดที่เกี่ยวข้องกับโมเดล รวมถึงการลงทุนทรัพยากรอัลกอริทึมเทคนิค ฯลฯ

ปัญหาที่แท้จริงประการหนึ่งที่นักวิเคราะห์การจำลองต้องเผชิญคือการตรวจสอบความถูกต้องของแบบจำลอง แบบจำลองจะใช้ได้เฉพาะในกรณีที่แบบจำลองเป็นตัวแทนที่ถูกต้องของระบบจริงมิฉะนั้นจะไม่ถูกต้อง

การตรวจสอบความถูกต้องและการตรวจสอบเป็นสองขั้นตอนในโครงการจำลองเพื่อตรวจสอบความถูกต้องของโมเดล

• Validationเป็นกระบวนการเปรียบเทียบผลลัพธ์สองรายการ ในกระบวนการนี้เราจำเป็นต้องเปรียบเทียบการเป็นตัวแทนของแบบจำลองความคิดกับระบบจริง หากการเปรียบเทียบเป็นจริงแสดงว่าถูกต้องไม่ถูกต้อง

• Verificationเป็นกระบวนการเปรียบเทียบผลลัพธ์สองรายการขึ้นไปเพื่อให้แน่ใจว่าถูกต้อง ในกระบวนการนี้เราจะต้องเปรียบเทียบการนำโมเดลไปใช้งานและข้อมูลที่เกี่ยวข้องกับคำอธิบายและข้อกำหนดเชิงแนวคิดของผู้พัฒนา

เทคนิคการตรวจสอบและการตรวจสอบความถูกต้อง

มีเทคนิคต่างๆที่ใช้ในการดำเนินการ Verification & Validation of Simulation Model ต่อไปนี้เป็นเทคนิคทั่วไปบางส่วน -

เทคนิคในการตรวจสอบโมเดลจำลอง

ต่อไปนี้เป็นวิธีการตรวจสอบโมเดลจำลอง -

• โดยใช้ทักษะการเขียนโปรแกรมเพื่อเขียนและแก้จุดบกพร่องของโปรแกรมในโปรแกรมย่อย.

• โดยใช้นโยบาย "Structured Walk-through" ที่มีคนอ่านโปรแกรมมากกว่าหนึ่งคน

• โดยการติดตามผลลัพธ์ระดับกลางและเปรียบเทียบกับผลลัพธ์ที่สังเกตได้

• โดยการตรวจสอบผลลัพธ์ของโมเดลจำลองโดยใช้ชุดอินพุตต่างๆ

• โดยการเปรียบเทียบผลการจำลองขั้นสุดท้ายกับผลการวิเคราะห์

เทคนิคการตรวจสอบความถูกต้องของแบบจำลอง

Step 1- ออกแบบโมเดลที่มีความถูกต้องสูง สามารถทำได้โดยใช้ขั้นตอนต่อไปนี้ -

• โมเดลจะต้องได้รับการหารือกับผู้เชี่ยวชาญของระบบในขณะที่ออกแบบ
• โมเดลต้องโต้ตอบกับไคลเอ็นต์ตลอดกระบวนการ
• ผลลัพธ์ต้องดูแลโดยผู้เชี่ยวชาญระบบ

Step 2- ทดสอบแบบจำลองที่ข้อมูลสมมติฐาน สิ่งนี้สามารถทำได้โดยการใช้ข้อมูลสมมติฐานในแบบจำลองและทดสอบในเชิงปริมาณ นอกจากนี้ยังสามารถทำการวิเคราะห์ที่ละเอียดอ่อนเพื่อสังเกตผลของการเปลี่ยนแปลงในผลลัพธ์เมื่อมีการเปลี่ยนแปลงที่สำคัญในข้อมูลอินพุต

Step 3- กำหนดผลลัพธ์ที่เป็นตัวแทนของโมเดลจำลอง สามารถทำได้โดยใช้ขั้นตอนต่อไปนี้ -

• กำหนดว่าเอาต์พุตการจำลองใกล้เคียงกับเอาต์พุตระบบจริงแค่ไหน

• การเปรียบเทียบสามารถทำได้โดยใช้การทดสอบทัวริง นำเสนอข้อมูลในรูปแบบระบบซึ่งสามารถอธิบายได้โดยผู้เชี่ยวชาญเท่านั้น

• วิธีการทางสถิติสามารถใช้เพื่อเปรียบเทียบเอาต์พุตของโมเดลกับเอาต์พุตของระบบจริง

การเปรียบเทียบข้อมูลแบบจำลองกับข้อมูลจริง

หลังจากการพัฒนาโมเดลเราต้องทำการเปรียบเทียบข้อมูลผลลัพธ์กับข้อมูลระบบจริง ต่อไปนี้เป็นสองวิธีในการเปรียบเทียบนี้

การตรวจสอบความถูกต้องของระบบที่มีอยู่

ในแนวทางนี้เราใช้ปัจจัยการผลิตในโลกแห่งความเป็นจริงของแบบจำลองเพื่อเปรียบเทียบผลลัพธ์ของมันกับอินพุตจริงของระบบจริง กระบวนการตรวจสอบความถูกต้องนี้ตรงไปตรงมา แต่อาจมีปัญหาบางอย่างเมื่อดำเนินการเช่นหากต้องเปรียบเทียบผลลัพธ์กับความยาวเฉลี่ยเวลารอเวลาว่าง ฯลฯ สามารถเปรียบเทียบได้โดยใช้การทดสอบทางสถิติและการทดสอบสมมติฐาน การทดสอบทางสถิติบางอย่าง ได้แก่ การทดสอบไคสแควร์การทดสอบ Kolmogorov-Smirnov การทดสอบ Cramer-von Mises และการทดสอบ Moments

การตรวจสอบความถูกต้องของโมเดลครั้งแรก

พิจารณาว่าเราต้องอธิบายระบบที่เสนอซึ่งไม่มีอยู่ในปัจจุบันและไม่มีอยู่ในอดีต ดังนั้นจึงไม่มีข้อมูลในอดีตที่จะเปรียบเทียบประสิทธิภาพด้วย ดังนั้นเราต้องใช้ระบบสมมุติตามสมมติฐาน การปฏิบัติตามคำแนะนำที่เป็นประโยชน์จะช่วยในการทำให้มีประสิทธิภาพ

• Subsystem Validity- ตัวแบบเองอาจไม่มีระบบที่มีอยู่ให้เปรียบเทียบได้ แต่อาจประกอบด้วยระบบย่อยที่รู้จัก แต่ละความถูกต้องนั้นสามารถทดสอบแยกกันได้

• Internal Validity - แบบจำลองที่มีความแปรปรวนภายในระดับสูงจะถูกปฏิเสธเนื่องจากเป็นระบบสุ่มที่มีความแปรปรวนสูงเนื่องจากกระบวนการภายในจะซ่อนการเปลี่ยนแปลงในเอาต์พุตเนื่องจากการเปลี่ยนแปลงอินพุต

• Sensitivity Analysis - ให้ข้อมูลเกี่ยวกับพารามิเตอร์ที่ละเอียดอ่อนในระบบที่เราต้องให้ความสนใจมากขึ้น

• Face Validity - เมื่อโมเดลทำงานบนลอจิกตรงกันข้ามควรปฏิเสธแม้ว่าโมเดลจะทำงานเหมือนระบบจริงก็ตาม

ในระบบที่ไม่ต่อเนื่องการเปลี่ยนแปลงสถานะของระบบจะไม่ต่อเนื่องและการเปลี่ยนแปลงแต่ละครั้งในสถานะของระบบเรียกว่า event. แบบจำลองที่ใช้ในการจำลองระบบไม่ต่อเนื่องมีชุดตัวเลขเพื่อแสดงสถานะของระบบเรียกว่า astate descriptor. ในบทนี้เราจะได้เรียนรู้เกี่ยวกับการจำลองการเข้าคิวซึ่งเป็นสิ่งที่สำคัญมากในการจำลองเหตุการณ์แบบไม่ต่อเนื่องพร้อมกับการจำลองระบบแบ่งเวลา

ต่อไปนี้คือการแสดงลักษณะกราฟิกของพฤติกรรมของการจำลองระบบที่ไม่ต่อเนื่อง

การจำลองเหตุการณ์ไม่ต่อเนื่อง─คุณสมบัติหลัก

โดยทั่วไปการจำลองเหตุการณ์แบบไม่ต่อเนื่องจะดำเนินการโดยซอฟต์แวร์ที่ออกแบบด้วยภาษาโปรแกรมระดับสูงเช่น Pascal, C ++ หรือภาษาจำลองเฉพาะทาง คุณสมบัติหลักห้าประการต่อไปนี้ -

• Entities - สิ่งเหล่านี้คือการแสดงองค์ประกอบจริงเช่นชิ้นส่วนของเครื่องจักร

• Relationships - หมายถึงการเชื่อมโยงเอนทิตีเข้าด้วยกัน

• Simulation Executive - มีหน้าที่ควบคุมเวลาล่วงหน้าและดำเนินเหตุการณ์ที่ไม่ต่อเนื่อง

• Random Number Generator - ช่วยในการจำลองข้อมูลต่างๆที่เข้ามาในโมเดลจำลอง

• Results & Statistics - ตรวจสอบความถูกต้องของโมเดลและจัดเตรียมการวัดประสิทธิภาพ

การแสดงกราฟเวลา

ทุกระบบขึ้นอยู่กับพารามิเตอร์เวลา ในการแสดงภาพกราฟิกจะเรียกว่าเวลานาฬิกาหรือตัวนับเวลาและในตอนแรกจะตั้งค่าเป็นศูนย์ เวลาจะอัปเดตตามปัจจัยสองประการต่อไปนี้ -

• Time Slicing - เป็นเวลาที่กำหนดโดยโมเดลสำหรับแต่ละเหตุการณ์จนกว่าจะไม่มีเหตุการณ์ใด ๆ

• Next Event- เป็นเหตุการณ์ที่กำหนดโดยโมเดลสำหรับเหตุการณ์ถัดไปที่จะดำเนินการแทนช่วงเวลา มีประสิทธิภาพมากกว่าการแบ่งเวลา

การจำลองระบบจัดคิว

คิวคือการรวมกันของเอนทิตีทั้งหมดในระบบที่กำลังเสิร์ฟและผู้ที่รอการถึงตา

พารามิเตอร์

ต่อไปนี้เป็นรายการพารามิเตอร์ที่ใช้ในระบบคิว

สัญลักษณ์	คำอธิบาย
λ	หมายถึงอัตราการมาถึงซึ่งเป็นจำนวนการมาถึงต่อวินาที
Ts	หมายถึงเวลาให้บริการเฉลี่ยสำหรับการมาถึงแต่ละครั้งโดยไม่รวมเวลารอในคิว
σTs	หมายถึงค่าเบี่ยงเบนมาตรฐานของเวลาให้บริการ
ρ	หมายถึงการใช้เวลาของเซิร์ฟเวอร์ทั้งในขณะที่ไม่มีการใช้งานและไม่ว่าง
ยู	หมายถึงความเข้มของการจราจร
ร	หมายถึงค่าเฉลี่ยของรายการในระบบ
ร	หมายถึงจำนวนรายการทั้งหมดในระบบ
ทร	หมายถึงเวลาเฉลี่ยของไอเท็มในระบบ
ทร	หมายถึงเวลาทั้งหมดของไอเท็มในระบบ
σr	หมายถึงค่าเบี่ยงเบนมาตรฐานของ r
σTr	หมายถึงค่าเบี่ยงเบนมาตรฐานของ Tr
ว	หมายถึงจำนวนรายการที่รอคิวโดยเฉลี่ย
σw	หมายถึงค่าเบี่ยงเบนมาตรฐานของ w
Tw	หมายถึงเวลารอเฉลี่ยของรายการทั้งหมด
Td	หมายถึงเวลารอเฉลี่ยของรายการที่รอคิว
น	หมายถึงจำนวนเซิร์ฟเวอร์ในระบบ
mx (y)	หมายถึงวายTHเปอร์เซ็นต์ซึ่งหมายความว่าค่าของ Y ด้านล่างซึ่ง x เกิดขึ้นร้อยละปีของเวลา

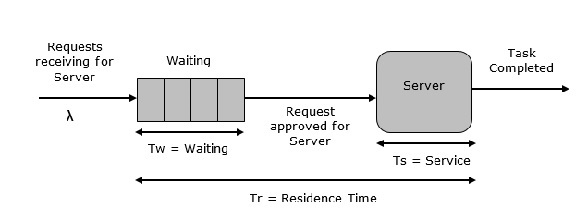
คิวเซิร์ฟเวอร์เดียว

นี่เป็นระบบการจัดคิวที่ง่ายที่สุดดังแสดงในรูปต่อไปนี้ องค์ประกอบกลางของระบบคือเซิร์ฟเวอร์ซึ่งให้บริการกับอุปกรณ์หรือรายการที่เชื่อมต่อ รายการร้องขอไปยังระบบที่จะให้บริการหากเซิร์ฟเวอร์ไม่ได้ใช้งาน จากนั้นจะเสิร์ฟทันทีมิฉะนั้นจะเข้าร่วมคิวรอ หลังจากงานเสร็จสิ้นโดยเซิร์ฟเวอร์รายการจะออกไป

คิวหลายเซิร์ฟเวอร์

ตามชื่อที่แนะนำระบบประกอบด้วยเซิร์ฟเวอร์หลายเครื่องและคิวทั่วไปสำหรับรายการทั้งหมด เมื่อไอเท็มใด ๆ ร้องขอสำหรับเซิร์ฟเวอร์จะได้รับการจัดสรรหากมีเซิร์ฟเวอร์อย่างน้อยหนึ่งเซิร์ฟเวอร์ มิฉะนั้นคิวจะเริ่มต้นจนกว่าเซิร์ฟเวอร์จะว่าง ในระบบนี้เราถือว่าเซิร์ฟเวอร์ทั้งหมดเหมือนกันกล่าวคือไม่มีความแตกต่างกันว่าเซิร์ฟเวอร์ใดถูกเลือกสำหรับรายการใด

มีข้อยกเว้นของการใช้ประโยชน์ ปล่อยN เป็นเซิร์ฟเวอร์ที่เหมือนกันแล้ว ρคือการใช้ประโยชน์ของแต่ละเซิร์ฟเวอร์ พิจารณาNρเพื่อเป็นการใช้ประโยชน์ทั้งระบบ จากนั้นการใช้ประโยชน์สูงสุดคือN*100%และอัตราอินพุตสูงสุดคือ -

$ λmax = \ frac {\ text {N}} {\ text {T} s} $

การจัดคิวความสัมพันธ์

ตารางต่อไปนี้แสดงความสัมพันธ์ของการจัดคิวขั้นพื้นฐาน

ข้อกำหนดทั่วไป	เซิร์ฟเวอร์เดียว	เซิร์ฟเวอร์หลายเครื่อง
r = λTrสูตรของ Little	ρ = λTs	ρ = λTs / N
w = λTwสูตรของ Little	r = w + ρ	คุณ = λTs = ρN
Tr = Tw + Ts		r = w + Nρ

การจำลองระบบแบ่งเวลา

ระบบแบ่งปันเวลาได้รับการออกแบบในลักษณะที่ผู้ใช้แต่ละคนใช้เวลาส่วนน้อยที่ใช้ร่วมกันในระบบซึ่งส่งผลให้ผู้ใช้หลายคนแชร์ระบบพร้อมกัน การสลับผู้ใช้แต่ละคนรวดเร็วมากจนผู้ใช้แต่ละคนรู้สึกเหมือนใช้ระบบของตนเอง มันขึ้นอยู่กับแนวคิดของการตั้งเวลา CPU และการเขียนโปรแกรมหลายโปรแกรมซึ่งสามารถใช้ทรัพยากรหลายอย่างได้อย่างมีประสิทธิภาพโดยการดำเนินการหลายงานพร้อมกันบนระบบ

Example - ระบบจำลอง SimOS

ได้รับการออกแบบโดยมหาวิทยาลัยสแตนฟอร์ดเพื่อศึกษาการออกแบบฮาร์ดแวร์คอมพิวเตอร์ที่ซับซ้อนเพื่อวิเคราะห์ประสิทธิภาพของแอปพลิเคชันและศึกษาระบบปฏิบัติการ SimOS ประกอบด้วยการจำลองซอฟต์แวร์ของส่วนประกอบฮาร์ดแวร์ทั้งหมดของระบบคอมพิวเตอร์สมัยใหม่เช่นโปรเซสเซอร์หน่วยการจัดการหน่วยความจำ (MMU) แคชเป็นต้น

ระบบต่อเนื่องเป็นระบบที่กิจกรรมที่สำคัญของระบบดำเนินไปอย่างราบรื่นโดยไม่มีความล่าช้ากล่าวคือไม่มีคิวของเหตุการณ์ไม่มีการจำลองเวลาแบบเรียงลำดับเป็นต้นเมื่อระบบต่อเนื่องถูกจำลองแบบทางคณิตศาสตร์ตัวแปรที่แสดงถึงคุณลักษณะจะถูกควบคุมโดยฟังก์ชันต่อเนื่อง .

การจำลองแบบต่อเนื่องคืออะไร?

การจำลองแบบต่อเนื่องคือการจำลองประเภทหนึ่งที่ตัวแปรสถานะเปลี่ยนแปลงอย่างต่อเนื่องตามเวลา ต่อไปนี้คือการแสดงพฤติกรรมของมันในรูปแบบกราฟิก

เหตุใดจึงต้องใช้การจำลองแบบต่อเนื่อง

เราต้องใช้การจำลองแบบต่อเนื่องเนื่องจากขึ้นอยู่กับสมการเชิงอนุพันธ์ของพารามิเตอร์ต่างๆที่เกี่ยวข้องกับระบบและผลลัพธ์โดยประมาณที่เราทราบ

พื้นที่การใช้งาน

การจำลองแบบต่อเนื่องถูกใช้ในภาคต่อไปนี้ ในงานวิศวกรรมโยธาสำหรับการก่อสร้างเขื่อนและการสร้างอุโมงค์ ในการใช้งานทางทหารสำหรับการจำลองวิถีขีปนาวุธการจำลองการฝึกเครื่องบินรบและการออกแบบและทดสอบตัวควบคุมอัจฉริยะสำหรับยานพาหนะใต้น้ำ

ในด้านโลจิสติกส์สำหรับการออกแบบด่านเก็บค่าผ่านทางการวิเคราะห์การไหลของผู้โดยสารที่อาคารผู้โดยสารสนามบินและการประเมินตารางการบินเชิงรุก ในการพัฒนาธุรกิจสำหรับการวางแผนการพัฒนาผลิตภัณฑ์การวางแผนการจัดการพนักงานและการวิเคราะห์การศึกษาตลาด

การจำลองมอนติคาร์โลเป็นเทคนิคทางคณิตศาสตร์แบบคอมพิวเตอร์เพื่อสร้างข้อมูลตัวอย่างแบบสุ่มโดยอาศัยการแจกแจงที่รู้จักกันสำหรับการทดลองเชิงตัวเลข วิธีนี้ใช้กับการวิเคราะห์เชิงปริมาณความเสี่ยงและปัญหาการตัดสินใจ วิธีนี้ใช้โดยผู้เชี่ยวชาญด้านโปรไฟล์ต่างๆเช่นการเงินการจัดการโครงการพลังงานการผลิตวิศวกรรมการวิจัยและพัฒนาการประกันภัยน้ำมันและก๊าซการขนส่งเป็นต้น

วิธีนี้ถูกใช้ครั้งแรกโดยนักวิทยาศาสตร์ที่ทำงานกับระเบิดปรมาณูในปี พ.ศ. 2483 วิธีนี้สามารถใช้ได้ในสถานการณ์ที่เราจำเป็นต้องทำการประมาณการและการตัดสินใจที่ไม่แน่นอนเช่นการพยากรณ์อากาศ

การจำลองมอนติคาร์โล─ลักษณะสำคัญ

ต่อไปนี้เป็นลักษณะสำคัญสามประการของวิธีมอนติคาร์โล -

• ผลลัพธ์ต้องสร้างตัวอย่างแบบสุ่ม
• ต้องทราบการกระจายอินพุต
• ต้องทราบผลลัพธ์ขณะทำการทดลอง

การจำลองมอนติคาร์โล─ข้อดี

• ใช้งานง่าย
• ให้การสุ่มตัวอย่างทางสถิติสำหรับการทดลองเชิงตัวเลขโดยใช้คอมพิวเตอร์
• ให้วิธีแก้ปัญหาทางคณิตศาสตร์โดยประมาณ
• สามารถใช้ได้กับทั้งปัญหาสุ่มและปัญหา

การจำลองมอนติคาร์โล─ข้อเสีย

• ใช้เวลานานเนื่องจากจำเป็นต้องสร้างการสุ่มตัวอย่างจำนวนมากเพื่อให้ได้ผลลัพธ์ที่ต้องการ

• ผลลัพธ์ของวิธีนี้เป็นเพียงการประมาณค่าจริงเท่านั้นไม่ใช่ค่าที่แน่นอน

วิธีการจำลองมอนติคาร์โล─แผนผังการไหล

ภาพประกอบต่อไปนี้แสดงผังงานทั่วไปของการจำลองมอนติคาร์โล

วัตถุประสงค์ของฐานข้อมูลในการสร้างแบบจำลองและการจำลองคือการจัดเตรียมการแสดงข้อมูลและความสัมพันธ์เพื่อวัตถุประสงค์ในการวิเคราะห์และทดสอบ แบบจำลองข้อมูลแรกถูกนำมาใช้ในปี 1980 โดย Edgar Codd ต่อไปนี้เป็นคุณสมบัติเด่นของรุ่นนี้

• ฐานข้อมูลคือการรวบรวมวัตถุข้อมูลต่างๆที่กำหนดข้อมูลและความสัมพันธ์

• กฎมีไว้สำหรับกำหนดข้อ จำกัด ของข้อมูลในวัตถุ

• การดำเนินการสามารถนำไปใช้กับอ็อบเจ็กต์เพื่อดึงข้อมูล

ในขั้นต้นการสร้างแบบจำลองข้อมูลขึ้นอยู่กับแนวคิดของเอนทิตีและความสัมพันธ์ซึ่งเอนทิตีเป็นประเภทข้อมูลของข้อมูลและความสัมพันธ์แสดงถึงความสัมพันธ์ระหว่างเอนทิตี

แนวคิดล่าสุดสำหรับการสร้างแบบจำลองข้อมูลคือการออกแบบเชิงวัตถุซึ่งเอนทิตีถูกแสดงเป็นคลาสซึ่งใช้เป็นเทมเพลตในการเขียนโปรแกรมคอมพิวเตอร์ คลาสที่มีชื่อคุณลักษณะข้อ จำกัด และความสัมพันธ์กับอ็อบเจ็กต์ของคลาสอื่น

การแสดงพื้นฐานมีลักษณะดังนี้ -

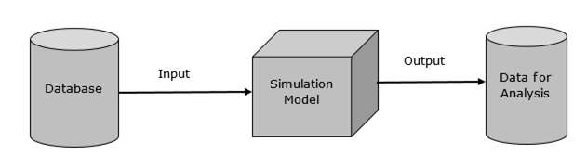
การแสดงข้อมูล

การแสดงข้อมูลสำหรับเหตุการณ์

เหตุการณ์จำลองมีแอตทริบิวต์เช่นชื่อเหตุการณ์และข้อมูลเวลาที่เกี่ยวข้อง แสดงถึงการดำเนินการของการจำลองที่จัดเตรียมไว้โดยใช้ชุดข้อมูลอินพุตที่เชื่อมโยงกับพารามิเตอร์ไฟล์อินพุตและให้ผลลัพธ์เป็นชุดข้อมูลเอาต์พุตที่จัดเก็บในไฟล์หลายไฟล์ที่เกี่ยวข้องกับไฟล์ข้อมูล

การแสดงข้อมูลสำหรับไฟล์อินพุต

ทุกกระบวนการจำลองต้องการชุดข้อมูลอินพุตที่แตกต่างกันและค่าพารามิเตอร์ที่เกี่ยวข้องซึ่งแสดงในไฟล์ข้อมูลอินพุต ไฟล์อินพุตเชื่อมโยงกับซอฟต์แวร์ที่ประมวลผลการจำลอง โมเดลข้อมูลแสดงถึงไฟล์ที่อ้างอิงโดยการเชื่อมโยงกับไฟล์ข้อมูล

การแสดงข้อมูลสำหรับไฟล์เอาต์พุต

เมื่อกระบวนการจำลองเสร็จสมบูรณ์จะสร้างไฟล์เอาต์พุตต่างๆและไฟล์เอาต์พุตแต่ละไฟล์จะแสดงเป็นไฟล์ข้อมูล แต่ละไฟล์มีชื่อคำอธิบายและปัจจัยที่เป็นสากล ไฟล์ข้อมูลแบ่งออกเป็นสองไฟล์ ไฟล์แรกมีค่าตัวเลขและไฟล์ที่สองมีข้อมูลอธิบายเนื้อหาของไฟล์ตัวเลข

โครงข่ายประสาทเทียมในการสร้างแบบจำลองและการจำลองสถานการณ์

เครือข่ายประสาทเทียมเป็นสาขาของปัญญาประดิษฐ์ เครือข่ายประสาทเทียมเป็นเครือข่ายของหน่วยประมวลผลหลายตัวที่เรียกว่าหน่วยแต่ละหน่วยมีหน่วยความจำภายในขนาดเล็ก แต่ละหน่วยเชื่อมต่อด้วยช่องทางการสื่อสารทิศทางเดียวที่เรียกว่าการเชื่อมต่อซึ่งมีข้อมูลตัวเลข แต่ละหน่วยจะทำงานเฉพาะกับข้อมูลในเครื่องและอินพุตที่ได้รับจากการเชื่อมต่อ

ประวัติศาสตร์

มุมมองทางประวัติศาสตร์ของการจำลองจะแจกแจงตามลำดับเวลา

แบบจำลองประสาทแรกได้รับการพัฒนาใน 1940 โดย McCulloch & Pitts

ใน 1949โดนัลด์เฮบบ์เขียนหนังสือ“ องค์การแห่งพฤติกรรม” ซึ่งชี้ให้เห็นถึงแนวคิดของเซลล์ประสาท

ใน 1950เนื่องจากคอมพิวเตอร์มีความก้าวหน้าจึงสามารถสร้างแบบจำลองของทฤษฎีเหล่านี้ได้ ทำโดยห้องปฏิบัติการวิจัยของไอบีเอ็ม อย่างไรก็ตามความพยายามล้มเหลวและความพยายามในภายหลังก็ประสบความสำเร็จ

ใน 1959, Bernard Widrow และ Marcian Hoff พัฒนาโมเดลที่เรียกว่า ADALINE และ MADALINE โมเดลเหล่านี้มี ADAptive LINear Elements หลายตัว MADALINE เป็นโครงข่ายประสาทเทียมแห่งแรกที่ใช้กับปัญหาในโลกแห่งความเป็นจริง

ใน 1962แบบจำลอง perceptron ได้รับการพัฒนาโดย Rosenblatt ซึ่งมีความสามารถในการแก้ปัญหาการจำแนกรูปแบบอย่างง่าย

ใน 1969Minsky & Papert ให้การพิสูจน์ทางคณิตศาสตร์เกี่ยวกับข้อ จำกัด ของแบบจำลอง perceptron ในการคำนวณ ว่ากันว่าแบบจำลองเพอร์เซปตรอนไม่สามารถแก้ปัญหา X-OR ได้ ข้อบกพร่องดังกล่าวนำไปสู่การลดลงของเครือข่ายประสาทเทียมชั่วคราว

ใน 1982จอห์นฮอปฟิลด์แห่งคาลเทคได้นำเสนอแนวคิดของเขาบนกระดาษต่อ National Academy of Sciences เพื่อสร้างเครื่องจักรโดยใช้เส้นสองทิศทาง ก่อนหน้านี้มีการใช้เส้นทิศทางเดียว

เมื่อเทคนิคปัญญาประดิษฐ์แบบดั้งเดิมที่เกี่ยวข้องกับวิธีการสัญลักษณ์ล้มเหลวจึงจำเป็นต้องใช้เครือข่ายประสาทเทียม โครงข่ายประสาทเทียมมีเทคนิคการขนานใหญ่ซึ่งให้พลังคอมพิวเตอร์ที่จำเป็นในการแก้ปัญหาดังกล่าว

พื้นที่การใช้งาน

โครงข่ายประสาทเทียมสามารถใช้ในเครื่องสังเคราะห์เสียงสำหรับการจดจำรูปแบบเพื่อตรวจหาปัญหาในการวินิจฉัยในแผงควบคุมหุ่นยนต์และอุปกรณ์ทางการแพทย์

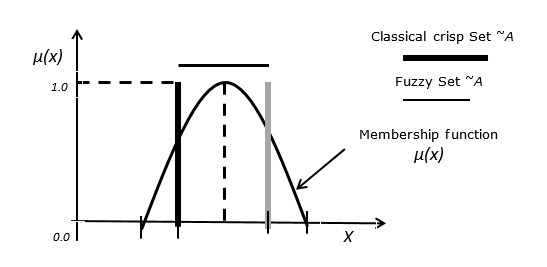
Fuzzy Set ในการสร้างแบบจำลองและการจำลองสถานการณ์

ตามที่กล่าวไว้ก่อนหน้านี้แต่ละกระบวนการของการจำลองแบบต่อเนื่องขึ้นอยู่กับสมการเชิงอนุพันธ์และพารามิเตอร์เช่น a, b, c, d> 0 โดยทั่วไปการประมาณค่าจุดจะถูกคำนวณและใช้ในแบบจำลอง อย่างไรก็ตามบางครั้งค่าประมาณเหล่านี้ไม่แน่นอนดังนั้นเราจึงต้องการตัวเลขที่ไม่ชัดเจนในสมการเชิงอนุพันธ์ซึ่งให้ค่าประมาณของพารามิเตอร์ที่ไม่รู้จัก

Fuzzy Set คืออะไร?

ในเซตคลาสสิกองค์ประกอบจะเป็นสมาชิกของเซตหรือไม่ก็ได้ เซตฟัซซีถูกกำหนดในรูปแบบของเซตคลาสสิกX เป็น -

A = {(x, μA (x)) | x ∈ X}

Case 1 - ฟังก์ชั่น μA(x) มีคุณสมบัติดังต่อไปนี้ -

∀x∈ X μA (x) ≥ 0

sup x ∈ X {μA (x)} = 1

Case 2 - ปล่อยให้คลุมเครือ B กำหนดเป็น A = {(3, 0.3), (4, 0.7), (5, 1), (6, 0.4)}จากนั้นสัญกรณ์ฟัซซีมาตรฐานจะเขียนเป็น A = {0.3/3, 0.7/4, 1/5, 0.4/6}

ค่าใด ๆ ที่มีระดับความเป็นสมาชิกเป็นศูนย์จะไม่ปรากฏในนิพจน์ของชุด

Case 3 - ความสัมพันธ์ระหว่างเซ็ตฟัซซี่กับเซ็ตกรอบคลาสสิก

รูปต่อไปนี้แสดงให้เห็นถึงความสัมพันธ์ระหว่างเซตฟัซซีกับเซตคลาสสิกที่คมชัด