ฟิสิกส์ - ความโน้มถ่วง
บทนำ
วัตถุท้องฟ้าทั้งหมดที่พบในจักรวาลดึงดูดซึ่งกันและกันและแรงดึงดูดระหว่างร่างกายเหล่านี้เรียกว่าเป็น gravitational force.

กฎแห่งความโน้มถ่วงสากล
วัตถุทุกชิ้นในจักรวาลมีคุณสมบัติในการดึงดูดวัตถุอื่น ๆ ด้วยแรงซึ่งเป็นสัดส่วนโดยตรงกับผลคูณของมวลของพวกมันและแปรผกผันกับกำลังสองของระยะห่างระหว่างพวกมัน (ดูภาพด้านล่าง)
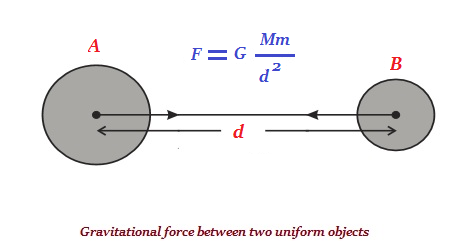
F = แรงดึงดูดระหว่างสองวัตถุ 'A' & 'B'
M = มวลของ 'A'
m = มวลของ 'B'
d2 = กำลังสองของระยะห่างระหว่าง 'A' & 'B'
G = คือค่าคงที่ของสัดส่วนและเรียกว่าค่าคงที่ความโน้มถ่วงสากล
หน่วย SI ของ G คือ N m2 kg–2. ได้จากการแทนหน่วยของแรงระยะทางและมวล (ดังที่ระบุในสมการต่อไปนี้ -
$$ G = \ frac {Fd ^ 2} {M \ times m} $$
Henry Cavendish ได้คำนวณมูลค่าของ ‘G’ เช่น 6.673 × 10–11 N m2 kg–2.
Henry Cavendish ใช้เครื่องชั่งที่ละเอียดอ่อนเพื่อหาค่าของ 'G. '
ความสำคัญของกฎความโน้มถ่วงสากล
ต่อไปนี้เป็นความสำคัญที่โดดเด่นของกฎความโน้มถ่วงสากล -
อธิบายถึงแรงที่ผูกมัดวัตถุทั้งหมด (รวมทั้งมนุษย์) กับโลก
อธิบายการเคลื่อนที่ของดวงจันทร์รอบโลก
อธิบายการเคลื่อนที่ของดาวเคราะห์รอบดวงอาทิตย์
มันชี้แจงกระแสน้ำเนื่องจากดวงจันทร์และดวงอาทิตย์
ฤดูใบไม้ร่วงฟรี
เมื่อใดก็ตามที่วัตถุตกลงสู่พื้นโลกจะมีการเร่งความเร็ว ความเร่งนี้เกิดขึ้นเนื่องจากแรงโน้มถ่วงของโลก

ความเร่งก่อให้เกิดเนื่องจากแรงโน้มถ่วงของโลกเรียกว่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก (หรือความเร่งเนื่องจากแรงโน้มถ่วง)
ความเร่งก่อให้เกิดเนื่องจากแรงโน้มถ่วงแสดงโดย g.
เมื่อรัศมีของโลกเพิ่มขึ้นไปทางเส้นศูนย์สูตร (จากขั้ว) ค่าของ ‘g’ จะมีค่ามากขึ้นที่ขั้วมากกว่าที่เส้นศูนย์สูตร
มูลค่าของ g
ค่าของ g คำนวณได้จาก -
$$ g = G \ frac {M} {R ^ 2} $$
G = ค่าคงที่ความโน้มถ่วงสากลซึ่งก็คือ = 6.7 × 10–11 N m2 kg-2
M = มวลของโลกซึ่งก็คือ = 6 × 1024 kg
R = รัศมีของโลกซึ่งก็คือ = 6.4 × 106 m
So,
$$ g = \ frac {6.7 \: \ times 10 ^ {- 11} \: Nm ^ 2 \: kg ^ {- 2} \: \ times \: 6 \: \ times 10 ^ {24} \: kg } {(6.4 \: \ คูณ 10 ^ 6 \: m) ^ 2} $$
$ = 9.8 \: m \: s ^ {- 2} $
ดังนั้นค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก (g) คือ 9.8 มิลลิวินาที-2