กราฟเชิงคำนวณ

Backpropagation ถูกนำไปใช้ในกรอบการเรียนรู้เชิงลึกเช่น Tensorflow, Torch, Theano เป็นต้นโดยใช้กราฟเชิงคำนวณ ที่สำคัญยิ่งไปกว่านั้นการทำความเข้าใจเกี่ยวกับการแพร่กระจายย้อนกลับบนกราฟการคำนวณจะรวมอัลกอริทึมที่แตกต่างกันหลายอย่างและรูปแบบต่างๆเช่น backprop ผ่านเวลาและ backprop ด้วยน้ำหนักที่ใช้ร่วมกัน เมื่อทุกอย่างถูกแปลงเป็นกราฟการคำนวณแล้วก็ยังคงเป็นอัลกอริทึมเดิม - เพียงแค่กลับการเผยแพร่บนกราฟการคำนวณ

Computational Graph คืออะไร

กราฟการคำนวณถูกกำหนดให้เป็นกราฟกำกับโดยที่โหนดสอดคล้องกับการดำเนินการทางคณิตศาสตร์ กราฟเชิงคำนวณเป็นวิธีการแสดงและประเมินนิพจน์ทางคณิตศาสตร์

ตัวอย่างเช่นนี่คือสมการทางคณิตศาสตร์อย่างง่าย -

$$ p = x + y $$

เราสามารถวาดกราฟการคำนวณของสมการข้างต้นได้ดังนี้

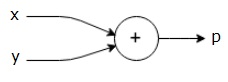
กราฟการคำนวณด้านบนมีโหนดเพิ่มเติม (โหนดที่มีเครื่องหมาย "+") ที่มีตัวแปรอินพุตสองตัว x และ y และหนึ่งเอาต์พุต q

ให้เราใช้ตัวอย่างอื่นที่ซับซ้อนกว่าเล็กน้อย เรามีสมการดังต่อไปนี้

$$ g = \ left (x + y \ right) \ ast z $$

สมการข้างต้นแสดงด้วยกราฟการคำนวณต่อไปนี้

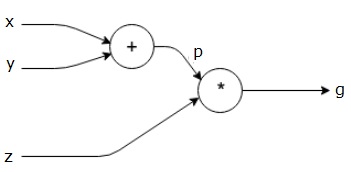
กราฟเชิงคำนวณและ Backpropagation

กราฟเชิงคำนวณและ backpropagation ทั้งสองเป็นแนวคิดหลักที่สำคัญในการเรียนรู้เชิงลึกสำหรับการฝึกอบรมเครือข่ายประสาทเทียม

ส่งต่อ

ส่งต่อเป็นขั้นตอนในการประเมินค่าของนิพจน์ทางคณิตศาสตร์ที่แสดงโดยกราฟเชิงคำนวณ การส่งต่อหมายความว่าเรากำลังส่งค่าจากตัวแปรในทิศทางไปข้างหน้าจากทางซ้าย (อินพุต) ไปทางขวาที่เอาต์พุตอยู่

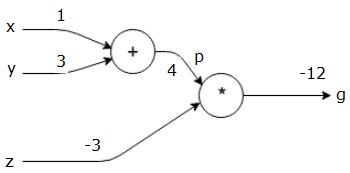
ให้เราพิจารณาตัวอย่างโดยการให้คุณค่ากับปัจจัยการผลิตทั้งหมด สมมติว่าค่าต่อไปนี้ถูกกำหนดให้กับอินพุตทั้งหมด

$$ x = 1, y = 3, z = −3 $$

ด้วยการให้ค่าเหล่านี้กับอินพุตเราสามารถทำการส่งต่อและรับค่าต่อไปนี้สำหรับเอาต์พุตในแต่ละโหนด

ขั้นแรกเราใช้ค่าของ x = 1 และ y = 3 เพื่อให้ได้ p = 4

จากนั้นเราใช้ p = 4 และ z = -3 เพื่อรับ g = -12 จากซ้ายไปขวาไปข้างหน้า

วัตถุประสงค์ของ Backward Pass

ในการส่งย้อนกลับความตั้งใจของเราคือการคำนวณการไล่ระดับสีสำหรับแต่ละอินพุตที่เกี่ยวข้องกับผลลัพธ์สุดท้าย การไล่ระดับสีเหล่านี้จำเป็นสำหรับการฝึกโครงข่ายประสาทโดยใช้การไล่ระดับสี

ตัวอย่างเช่นเราต้องการการไล่ระดับสีต่อไปนี้

การไล่ระดับสีที่ต้องการ

$$ \ frac {\ partial x} {\ partial f}, \ frac {\ partial y} {\ partial f}, \ frac {\ partial z} {\ partial f} $$

ย้อนกลับ (backpropagation)

เราเริ่มต้นการย้อนกลับโดยการหาอนุพันธ์ของผลลัพธ์สุดท้ายเทียบกับผลลัพธ์สุดท้าย (ตัวมันเอง!) ดังนั้นมันจะส่งผลให้เกิดเอกลักษณ์และค่าเท่ากับหนึ่ง

$$ \ frac {\ partial g} {\ partial g} = 1 $$

กราฟการคำนวณของเรามีลักษณะดังที่แสดงด้านล่าง -

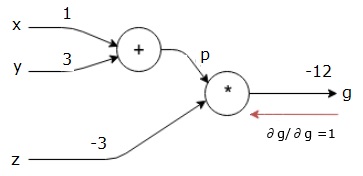
ต่อไปเราจะทำการย้อนกลับผ่านการดำเนินการ "*" เราจะคำนวณการไล่ระดับที่ p และ z เนื่องจาก g = p * z เรารู้ว่า -

$$ \ frac {\ partial g} {\ partial z} = p $$

$$ \ frac {\ partial g} {\ partial p} = z $$

เรารู้ค่า z และ p จากฟอร์เวิร์ดพาสแล้ว ดังนั้นเราจึงได้รับ -

$$ \ frac {\ partial g} {\ partial z} = p = 4 $$

และ

$$ \ frac {\ partial g} {\ partial p} = z = -3 $$

เราต้องการคำนวณการไล่ระดับสีที่ x และ y -

$$ \ frac {\ partial g} {\ partial x}, \ frac {\ partial g} {\ partial y} $$

อย่างไรก็ตามเราต้องการทำสิ่งนี้อย่างมีประสิทธิภาพ (แม้ว่า x และ g จะอยู่ห่างกันเพียงสองครั้งในกราฟนี้ แต่ลองนึกภาพพวกมันอยู่ไกลจากกันจริงๆ) ในการคำนวณค่าเหล่านี้อย่างมีประสิทธิภาพเราจะใช้กฎลูกโซ่ของความแตกต่าง จากกฎลูกโซ่เรามี -

$$ \ frac {\ partial g} {\ partial x} = \ frac {\ partial g} {\ partial p} \ ast \ frac {\ partial p} {\ partial x} $$

$$ \ frac {\ partial g} {\ partial y} = \ frac {\ partial g} {\ partial p} \ ast \ frac {\ partial p} {\ partial y} $$

แต่เรารู้แล้วว่า dg / dp = -3, dp / dx และ dp / dy นั้นง่ายเนื่องจาก p ขึ้นอยู่กับ x และ y โดยตรง เรามี -

$$ p = x + y \ Rightarrow \ frac {\ partial x} {\ partial p} = 1, \ frac {\ partial y} {\ partial p} = 1 $$

ดังนั้นเราจึงได้รับ -

$$ \ frac {\ partial g} {\ partial f} = \ frac {\ partial g} {\ partial p} \ ast \ frac {\ partial p} {\ partial x} = \ left (-3 \ right) .1 = -3 $$

นอกจากนี้สำหรับอินพุต y -

$$ \ frac {\ partial g} {\ partial y} = \ frac {\ partial g} {\ partial p} \ ast \ frac {\ partial p} {\ partial y} = \ left (-3 \ right) .1 = -3 $$

เหตุผลหลักในการทำสิ่งนี้ย้อนหลังคือเมื่อเราต้องคำนวณการไล่ระดับสีที่ x เราใช้เฉพาะค่าที่คำนวณแล้วและ dq / dx (อนุพันธ์ของโหนดเอาต์พุตเทียบกับอินพุตของโหนดเดียวกัน) เราใช้ข้อมูลในท้องถิ่นเพื่อคำนวณมูลค่าทั่วโลก

ขั้นตอนในการฝึกโครงข่ายประสาทเทียม

ทำตามขั้นตอนเหล่านี้เพื่อฝึกโครงข่ายประสาทเทียม -

• สำหรับจุดข้อมูล x ในชุดข้อมูลเราจะส่งต่อโดยใช้ x เป็นอินพุตและคำนวณต้นทุน c เป็นเอาต์พุต

• เราทำย้อนกลับโดยเริ่มต้นที่ c และคำนวณการไล่ระดับสีสำหรับโหนดทั้งหมดในกราฟ ซึ่งรวมถึงโหนดที่แสดงถึงน้ำหนักของโครงข่ายประสาทเทียม

• จากนั้นเราจะอัปเดตน้ำหนักโดยทำ W = W - อัตราการเรียนรู้ * การไล่ระดับสี

• เราทำขั้นตอนนี้ซ้ำจนกว่าจะตรงตามเกณฑ์การหยุด