TensorFlow - พื้นฐาน
ในบทนี้เราจะเรียนรู้เกี่ยวกับพื้นฐานของ TensorFlow เราจะเริ่มต้นด้วยการทำความเข้าใจโครงสร้างข้อมูลของเทนเซอร์
โครงสร้างข้อมูลเทนเซอร์
Tensors ใช้เป็นโครงสร้างข้อมูลพื้นฐานในภาษา TensorFlow Tensors แสดงขอบเชื่อมต่อในแผนภาพการไหลใด ๆ ที่เรียกว่า Data Flow Graph Tensors ถูกกำหนดให้เป็นอาร์เรย์หรือรายการหลายมิติ
Tensors ถูกระบุโดยพารามิเตอร์สามตัวต่อไปนี้ -
อันดับ
หน่วยของมิติที่อธิบายภายในเทนเซอร์เรียกว่าอันดับ ระบุจำนวนมิติของเทนเซอร์ อันดับของเทนเซอร์สามารถอธิบายได้ว่าเป็นลำดับหรือขนาด n ของเทนเซอร์ที่กำหนด
รูปร่าง
จำนวนแถวและคอลัมน์ร่วมกันกำหนดรูปร่างของ Tensor
ประเภท
Type อธิบายประเภทข้อมูลที่กำหนดให้กับองค์ประกอบของ Tensor
ผู้ใช้ต้องพิจารณากิจกรรมต่อไปนี้เพื่อสร้าง Tensor -
- สร้างอาร์เรย์ n มิติ
- แปลงอาร์เรย์ n มิติ
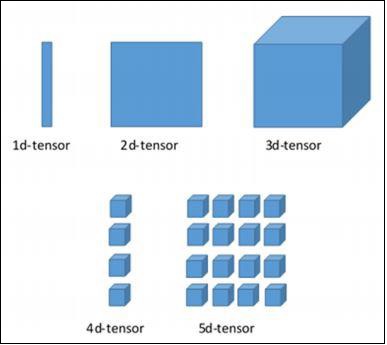
ขนาดต่างๆของ TensorFlow
TensorFlow ประกอบด้วยมิติข้อมูลต่างๆ มิติข้อมูลมีคำอธิบายสั้น ๆ ด้านล่าง -
Tensor หนึ่งมิติ
เทนเซอร์หนึ่งมิติเป็นโครงสร้างอาร์เรย์ปกติซึ่งรวมค่าหนึ่งชุดของประเภทข้อมูลเดียวกัน
Declaration
>>> import numpy as np
>>> tensor_1d = np.array([1.3, 1, 4.0, 23.99])
>>> print tensor_1dการใช้งานกับผลลัพธ์จะแสดงในภาพหน้าจอด้านล่าง -
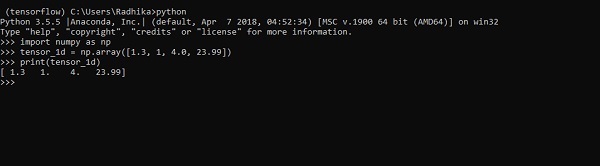
การสร้างดัชนีขององค์ประกอบจะเหมือนกับรายการ Python องค์ประกอบแรกเริ่มต้นด้วยดัชนี 0; ในการพิมพ์ค่าผ่านดัชนีสิ่งที่คุณต้องทำคือระบุหมายเลขดัชนี
>>> print tensor_1d[0]
1.3
>>> print tensor_1d[2]
4.0
Tensors สองมิติ
ลำดับของอาร์เรย์ใช้สำหรับการสร้าง "เทนเซอร์สองมิติ"
การสร้างเทนเซอร์สองมิติอธิบายไว้ด้านล่าง -

ต่อไปนี้เป็นไวยากรณ์ที่สมบูรณ์สำหรับการสร้างอาร์เรย์สองมิติ -
>>> import numpy as np
>>> tensor_2d = np.array([(1,2,3,4),(4,5,6,7),(8,9,10,11),(12,13,14,15)])
>>> print(tensor_2d)
[[ 1 2 3 4]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
>>>องค์ประกอบเฉพาะของเทนเซอร์สองมิติสามารถติดตามได้ด้วยความช่วยเหลือของหมายเลขแถวและหมายเลขคอลัมน์ที่ระบุเป็นหมายเลขดัชนี
>>> tensor_2d[3][2]
14
การจัดการและการจัดการ Tensor
ในส่วนนี้เราจะเรียนรู้เกี่ยวกับการจัดการและการจัดการเทนเซอร์
ในการเริ่มต้นให้เราพิจารณารหัสต่อไปนี้ -
import tensorflow as tf
import numpy as np
matrix1 = np.array([(2,2,2),(2,2,2),(2,2,2)],dtype = 'int32')
matrix2 = np.array([(1,1,1),(1,1,1),(1,1,1)],dtype = 'int32')
print (matrix1)
print (matrix2)
matrix1 = tf.constant(matrix1)
matrix2 = tf.constant(matrix2)
matrix_product = tf.matmul(matrix1, matrix2)
matrix_sum = tf.add(matrix1,matrix2)
matrix_3 = np.array([(2,7,2),(1,4,2),(9,0,2)],dtype = 'float32')
print (matrix_3)
matrix_det = tf.matrix_determinant(matrix_3)
with tf.Session() as sess:
result1 = sess.run(matrix_product)
result2 = sess.run(matrix_sum)
result3 = sess.run(matrix_det)
print (result1)
print (result2)
print (result3)Output
โค้ดด้านบนจะสร้างผลลัพธ์ต่อไปนี้ -
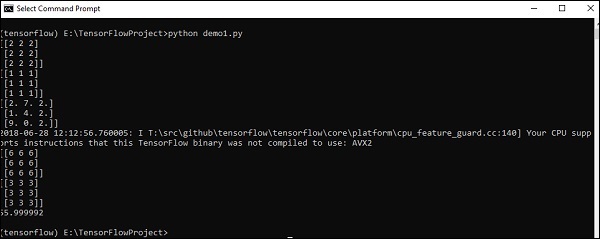
คำอธิบาย
เราได้สร้างอาร์เรย์หลายมิติในซอร์สโค้ดข้างต้น ตอนนี้สิ่งสำคัญคือต้องเข้าใจว่าเราสร้างกราฟและเซสชันซึ่งจัดการ Tensors และสร้างผลลัพธ์ที่เหมาะสม ด้วยความช่วยเหลือของกราฟเรามีผลลัพธ์ที่ระบุการคำนวณทางคณิตศาสตร์ระหว่าง Tensors