TensorFlow - พื้นฐานทางคณิตศาสตร์
สิ่งสำคัญคือต้องเข้าใจแนวคิดทางคณิตศาสตร์ที่จำเป็นสำหรับ TensorFlow ก่อนที่จะสร้างแอปพลิเคชันพื้นฐานใน TensorFlow คณิตศาสตร์ถือเป็นหัวใจของอัลกอริทึมการเรียนรู้ของเครื่อง ด้วยความช่วยเหลือของแนวคิดหลักของคณิตศาสตร์จึงมีการกำหนดโซลูชันสำหรับอัลกอริทึมการเรียนรู้ของเครื่องที่เฉพาะเจาะจง
เวกเตอร์
อาร์เรย์ของตัวเลขซึ่งไม่ว่าจะต่อเนื่องหรือไม่ต่อเนื่องถูกกำหนดให้เป็นเวกเตอร์ อัลกอริทึมการเรียนรู้ของเครื่องจัดการกับเวกเตอร์ที่มีความยาวคงที่เพื่อการสร้างเอาต์พุตที่ดีขึ้น
อัลกอริทึมการเรียนรู้ของเครื่องจัดการกับข้อมูลหลายมิติดังนั้นเวกเตอร์จึงมีบทบาทสำคัญ

การแสดงภาพของแบบจำลองเวกเตอร์มีดังที่แสดงด้านล่าง -
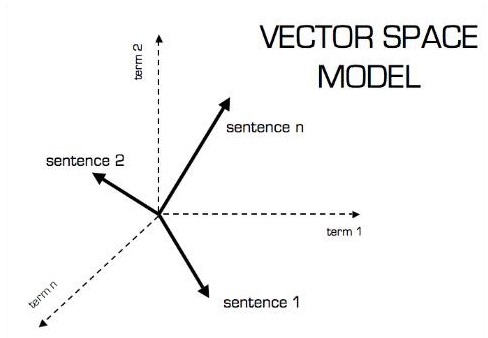
เกลา
สเกลาร์สามารถกำหนดเป็นเวกเตอร์มิติเดียว สเกลาร์คือสิ่งที่มีเพียงขนาดและไม่มีทิศทาง ด้วยสเกลาร์เราเกี่ยวข้องกับขนาดเท่านั้น
ตัวอย่างของสเกลาร์ ได้แก่ พารามิเตอร์น้ำหนักและส่วนสูงของเด็ก
เมทริกซ์
เมทริกซ์สามารถกำหนดเป็นอาร์เรย์หลายมิติซึ่งจัดเรียงในรูปแบบของแถวและคอลัมน์ ขนาดของเมทริกซ์ถูกกำหนดโดยความยาวแถวและความยาวของคอลัมน์ รูปต่อไปนี้แสดงการเป็นตัวแทนของเมทริกซ์ที่ระบุ
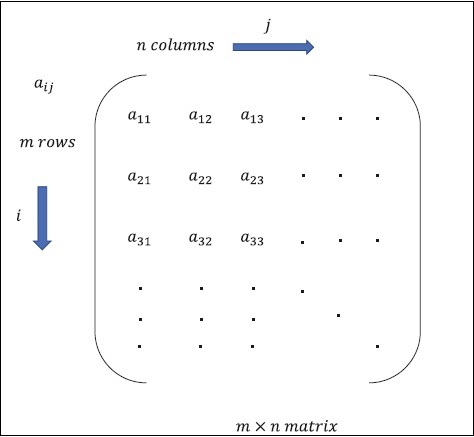
พิจารณาเมทริกซ์ที่มีแถว“ m” และคอลัมน์“ n” ตามที่กล่าวไว้ข้างต้นการแทนค่าเมทริกซ์จะถูกระบุเป็น“ เมทริกซ์ m * n” ซึ่งกำหนดความยาวของเมทริกซ์ด้วย
การคำนวณทางคณิตศาสตร์
ในส่วนนี้เราจะเรียนรู้เกี่ยวกับการคำนวณทางคณิตศาสตร์ต่างๆใน TensorFlow
การเพิ่มเมทริกซ์
สามารถเพิ่มเมทริกซ์สองตัวขึ้นไปได้หากเมทริกซ์มีมิติเดียวกัน การเพิ่มหมายถึงการเพิ่มของแต่ละองค์ประกอบตามตำแหน่งที่กำหนด
ลองพิจารณาตัวอย่างต่อไปนี้เพื่อทำความเข้าใจว่าการเพิ่มเมทริกซ์ทำงานอย่างไร -
$$ ตัวอย่าง: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: then \: A + B = \ begin {bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \ end {bmatrix} = \ begin {bmatrix} 6 & 8 \\ 10 & 12 \ end {bmatrix} $$
การลบเมทริกซ์
การลบเมทริกซ์ดำเนินการในลักษณะเดียวกันเช่นการบวกเมทริกซ์สองตัว ผู้ใช้สามารถลบเมทริกซ์สองตัวได้หากมิติข้อมูลเท่ากัน
$$ ตัวอย่าง: A- \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B- \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: then \: AB - \ begin {bmatrix} 1-5 & 2-6 \\ 3-7 & 4-8 \ end {bmatrix} - \ begin {bmatrix} -4 & -4 \\ - 4 & -4 \ end {bmatrix} $$
การคูณเมทริกซ์
สำหรับสองเมทริกซ์ A m * n และ B p * q ที่จะคูณได้ n ควรจะเท่ากับ p. เมทริกซ์ผลลัพธ์คือ -
ค m * q
$$ A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} $$
$$ c_ {11} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 1 \ times5 + 2 \ times7 = 19 \: c_ {12} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 1 \ times6 + 2 \ times8 = 22 $$
$$ c_ {21} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 3 \ times5 + 4 \ times7 = 43 \: c_ {22} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 3 \ times6 + 4 \ times8 = 50 $$
$$ C = \ begin {bmatrix} c_ {11} & c_ {12} \\ c_ {21} & c_ {22} \ end {bmatrix} = \ begin {bmatrix} 19 & 22 \\ 43 & 50 \ end {bmatrix} $$
การเปลี่ยนเมทริกซ์
ทรานสโพสของเมทริกซ์ A, m * n โดยทั่วไปจะแสดงด้วย AT (ทรานสโพส) n * m และหาได้จากการย้ายเวกเตอร์คอลัมน์เป็นเวกเตอร์แถว
$$ ตัวอย่าง: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \: then \: A ^ {T} \ begin {bmatrix} 1 & 3 \\ 2 & 4 \ end { bmatrix} $$
Dot product ของเวกเตอร์
เวกเตอร์ของมิติใด ๆ n สามารถแสดงเป็นเมทริกซ์ v = R ^ n * 1
$$ v_ {1} = \ begin {bmatrix} v_ {11} \\ v_ {12} \\\ cdot \\\ cdot \\\ cdot \\ v_ {1n} \ end {bmatrix} v_ {2} = \ start {bmatrix} v_ {21} \\ v_ {22} \\\ cdot \\\ cdot \\\ cdot \\ v_ {2n} \ end {bmatrix} $$
ดอทโปรดัคของเวกเตอร์สองตัวคือผลรวมของผลคูณของส่วนประกอบที่เกี่ยวข้อง - ส่วนประกอบในมิติเดียวกันและสามารถแสดงเป็น
$$ v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = v_2 ^ Tv_ {1} = v_ {11} v_ {21} + v_ {12} v_ {22} + \ cdot \ cdot + v_ {1n} v_ {2n} = \ displaystyle \ sum \ LIMIT_ {k = 1} ^ n v_ {1k} v_ {2k} $$
ตัวอย่างของ dot product ของเวกเตอร์มีดังต่อไปนี้ -
$$ ตัวอย่าง: v_ {1} = \ begin {bmatrix} 1 \\ 2 \\ 3 \ end {bmatrix} v_ {2} = \ begin {bmatrix} 3 \\ 5 \\ - 1 \ end {bmatrix} v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = 1 \ times3 + 2 \ times5-3 \ times1 = 10 $$