Derleyici Tasarımı - Sözdizimi Analizi

Sözdizimi analizi veya ayrıştırma, bir derleyicinin ikinci aşamasıdır. Bu bölümde, bir ayrıştırıcının yapımında kullanılan temel kavramları öğreneceğiz.

Bir sözcük analizcisinin, düzenli ifadeler ve kalıp kuralları yardımıyla simgeleri belirleyebileceğini gördük. Ancak bir sözcük analizcisi, düzenli ifadelerin sınırlamaları nedeniyle belirli bir cümlenin sözdizimini kontrol edemez. Normal ifadeler, parantez gibi dengeleme belirteçlerini kontrol edemez. Bu nedenle, bu aşama, aşağı itme otomatıyla tanınan bağlamdan bağımsız dilbilgisi (CFG) kullanır.

Öte yandan CFG, aşağıda tasvir edildiği gibi Düzenli Dilbilgisinin bir üst kümesidir:

Her Düzenli Dilbilgisinin bağlamdan bağımsız olduğu anlamına gelir, ancak Düzenli Dilbilgisinin kapsamı dışında kalan bazı sorunlar vardır. CFG, programlama dillerinin sözdizimini açıklamada yardımcı bir araçtır.

Bağlamdan Bağımsız Dilbilgisi

Bu bölümde, önce bağlamdan bağımsız dilbilgisinin tanımını görecek ve ayrıştırma teknolojisinde kullanılan terminolojileri tanıtacağız.

Bağlamdan bağımsız bir gramerin dört bileşeni vardır:

Bir dizi non-terminals(V). Terminal olmayanlar, dizgi setlerini ifade eden sözdizimsel değişkenlerdir. Terminal olmayanlar, dilbilgisi tarafından üretilen dili tanımlamaya yardımcı olan dize kümelerini tanımlar.
Olarak bilinen bir dizi jeton terminal symbols(Σ). Terminaller, dizelerin oluşturulduğu temel sembollerdir.
Bir dizi productions(P). Bir dilbilgisinin üretimleri, uçbirimlerin ve uçbirim olmayanların dizgiler oluşturmak için birleştirilme biçimini belirtir. Her üretim, birnon-terminal üretimin sol tarafı, bir ok ve bir dizi jeton ve / veya on- terminals, üretimin sağ tarafı olarak adlandırılır.
Terminal olmayanlardan biri, başlangıç sembolü (S) olarak belirtilir; üretimin başladığı yerden.

Dizeler, uç olmayanlar için bir üretimin sağ tarafıyla bir uç olmayan (başlangıçta başlangıç simgesi) tekrar tekrar değiştirilerek başlangıç simgesinden türetilir.

Misal

Düzenli İfade ile tanımlanamayan palindrom dili sorununu ele alıyoruz. Yani, L = {w | w = w ^R } normal bir dil değil. Ancak, aşağıda gösterildiği gibi CFG aracılığıyla açıklanabilir:

G = ( V, Σ, P, S )

Nerede:

V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }

Bu dilbilgisi, palindrom dilini açıklar, örneğin: 1001, 11100111, 00100, 1010101, 11111, vb.

Sözdizimi Çözümleyicileri

Bir sözdizimi çözümleyicisi veya ayrıştırıcısı, girdiyi bir sözcüksel çözümleyiciden belirteç akışları biçiminde alır. Ayrıştırıcı, koddaki hataları tespit etmek için kaynak kodunu (belirteç akışı) üretim kurallarına göre analiz eder. Bu fazın çıktısı birparse tree.

Bu şekilde, ayrıştırıcı iki görevi yerine getirir, yani, kodu ayrıştırmak, hataları aramak ve fazın çıktısı olarak bir ayrıştırma ağacı oluşturmak.

Programda bazı hatalar olsa bile ayrıştırıcıların tüm kodu ayrıştırması beklenir. Ayrıştırıcılar, bu bölümde daha sonra öğreneceğimiz hata düzeltme stratejilerini kullanır.

Türetme

Bir türetme, girdi dizgesini elde etmek için temelde bir üretim kuralları dizisidir. Ayrıştırma sırasında, bazı duygusal girdi biçimleri için iki karar alırız:

Değiştirilecek terminal olmayana karar verilmesi.
Terminal olmayanın değiştirileceği üretim kuralına karar verilmesi.

Üretim kuralı ile hangi terminal olmayanın değiştirileceğine karar vermek için iki seçeneğimiz olabilir.

En soldaki Türetme

Bir girdinin duygusal biçimi taranır ve soldan sağa değiştirilirse, buna en soldan türetme denir. En soldaki türetme tarafından türetilen duygusal biçim, sol-cümle biçimi olarak adlandırılır.

En Sağdaki Derivasyon

Girdiyi tarayıp, sağdan sola üretim kurallarıyla değiştirirsek, bu en sağdan türetme olarak bilinir. En sağdaki türetmeden türetilen cümlesel biçime sağ-cümle biçimi denir.

Example

Üretim kuralları:

E → E + E
E → E * E
E → id

Giriş dizesi: id + id * id

En soldaki türev şudur:

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

En soldaki terminal olmayan her zaman önce işlendiğine dikkat edin.

En sağdaki türetme şudur:

E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id

Ayrıştırma Ağacı

Ayrıştırma ağacı, türetmenin grafiksel bir tasviridir. Dizelerin başlangıç sembolünden nasıl türetildiğini görmek uygundur. Türetmenin başlangıç sembolü, ayrıştırma ağacının kökü olur. Bunu son konudan bir örnekle görelim.

A + b * c'nin en soldaki türevini alıyoruz

En soldaki türev şudur:

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

Aşama 1:

E → E * E

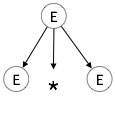
Adım 2:

E → E + E * E

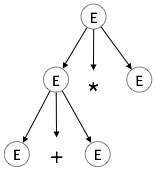
Aşama 3:

E → id + E * E

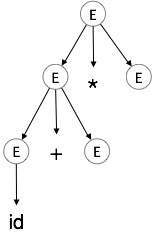
4. Adım:

E → id + id * E

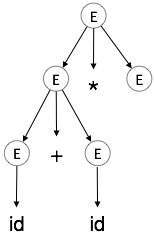
Adım 5:

E → id + id * id

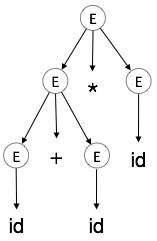
Ayrıştırma ağacında:

Tüm yaprak düğümler terminallerdir.
Tüm iç düğümler terminal değildir.
Sıralı geçiş, orijinal girdi dizesini verir.

Ayrıştırma ağacı, işleçlerin ilişkiselliğini ve önceliğini gösterir. İlk önce en derin alt ağaçtan geçilir, bu nedenle bu alt ağaçtaki operatör, üst düğümlerdeki operatörden öncelik kazanır.

Belirsizlik

En az bir dizge için birden fazla ayrıştırma ağacına (sol veya sağ türetme) sahipse gramer G'nin belirsiz olduğu söylenir.

Example

E → E + E
E → E – E
E → id

İd + id - id dizesi için yukarıdaki dilbilgisi iki ayrıştırma ağacı oluşturur:

Belirsiz bir dilbilgisi tarafından üretilen dilin inherently ambiguous. Dilbilgisindeki belirsizlik, bir derleyici yapısı için iyi değildir. Hiçbir yöntem belirsizliği otomatik olarak algılayıp ortadan kaldıramaz, ancak ya tüm grameri belirsizlik olmadan yeniden yazarak ya da çağrışım ve öncelik kısıtlamaları belirleyip takip ederek kaldırılabilir.

İlişkisellik

Bir işlenenin her iki tarafında da işleçler varsa, işlecin bu işleneni aldığı taraf, bu işleçlerin ilişkilendirilebilirliğine göre belirlenir. İşlem sola ilişkiliyse, işlenen sol operatör tarafından alınacak veya işlem sağla ilişkiliyse, sağ operatör işleneni alacaktır.

Example

Toplama, Çarpma, Çıkarma ve Bölme gibi işlemler ilişkisel olarak bırakılır. İfade içeriyorsa:

id op id op id

şu şekilde değerlendirilecektir:

(id op id) op id

Örneğin, (id + id) + id

Üs alma gibi işlemler doğru ilişkilidir, yani aynı ifadedeki değerlendirme sırası şöyle olacaktır:

id op (id op id)

Örneğin id ^ (id ^ id)

Öncelik

İki farklı operatör ortak bir operandı paylaşıyorsa, operatörlerin önceliği, hangisinin operandı alacağına karar verir. Yani, 2 + 3 * 4, biri (2 + 3) * 4'e ve diğeri 2+ (3 * 4) 'e karşılık gelen iki farklı ayrıştırma ağacına sahip olabilir. Operatörler arasında öncelik ayarlanarak bu sorun kolaylıkla giderilebilir. Önceki örnekte olduğu gibi, matematiksel olarak * (çarpma) + (toplama) üzerinde önceliğe sahiptir, bu nedenle 2 + 3 * 4 ifadesi her zaman şu şekilde yorumlanacaktır:

2 + (3 * 4)

Bu yöntemler, bir dilde veya dilbilgisinde belirsizlik olasılığını azaltır.

Sol Özyineleme

Bir dilbilgisi, türetilmesi en soldaki sembol olarak "A" nın kendisini içeren terminal olmayan bir "A" varsa, sol yinelemeli hale gelir. Sol-yinelemeli dilbilgisi, yukarıdan aşağıya ayrıştırıcılar için sorunlu bir durum olarak kabul edilir. Yukarıdan aşağıya ayrıştırıcılar, kendi içinde uçbirim olmayan Başlangıç sembolünden ayrıştırmaya başlar. Dolayısıyla, ayrıştırıcı türetilmesinde aynı uçbirim-dışı ile karşılaştığında, sol uç olmayanın ayrıştırmayı ne zaman durduracağını yargılaması zorlaşır ve sonsuz bir döngüye girer.

Example:

(1) A => Aα | β

(2) S => Aα | β 
    A => Sd

(1), hemen sol yinelemenin bir örneğidir, burada A herhangi bir terminal olmayan semboldür ve a, terminal olmayanların bir dizisini temsil eder.

(2) dolaylı-sol özyineleme örneğidir.

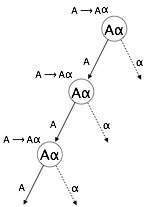
Yukarıdan aşağıya bir ayrıştırıcı önce A'yı ayrıştırır, bu da A'nın kendisinden oluşan bir dizge verir ve ayrıştırıcı sonsuza kadar bir döngüye girebilir.

Sol Özyinelemenin Kaldırılması

Sol özyinelemeyi kaldırmanın bir yolu aşağıdaki tekniği kullanmaktır:

Üretim

A => Aα | β

aşağıdaki yapımlara dönüştürülür

A => βA'
A'=> αA' | ε

Bu, gramerden türetilen dizeleri etkilemez, ancak hemen sol özyinelemeyi kaldırır.

İkinci yöntem, tüm doğrudan ve dolaylı sol yinelemeleri ortadan kaldırması gereken aşağıdaki algoritmayı kullanmaktır.

START

Arrange non-terminals in some order like A1, A2, A3,…, A_n

   for each i from 1 to n
      {
      for each j from 1 to i-1
         {
         replace each production of form A_i ⟹Aj
         with A_i ⟹ δ1  | δ2 | δ3 |…|  
         where A_j ⟹ δ₁ | δ₂|…| δ_n  are current A_j productions
         }
      }
   eliminate immediate left-recursion
   
END

Example

Üretim seti

S => Aα | β 
A => Sd

yukarıdaki algoritmayı uyguladıktan sonra,

S => Aα | β 
A => Aαd | βd

ve sonra, ilk tekniği kullanarak hemen sol özyinelemeyi kaldırın.

A  => βdA'
A' => αdA' | ε

Artık üretimin hiçbirinde doğrudan ya da dolaylı sol yineleme yok.

Sol Faktoring

Birden fazla dilbilgisi üretim kuralının ortak bir önek dizesi varsa, yukarıdan aşağı ayrıştırıcı, eldeki dizeyi ayrıştırmak için üretimden hangisinin gerekli olduğuna dair bir seçim yapamaz.

Example

Yukarıdan aşağıya bir ayrıştırıcı, aşağıdaki gibi bir üretimle karşılaşırsa

A ⟹ αβ | α | …

Ardından, her iki üretim de aynı terminalden (veya terminal olmayan) başladığından dizeyi ayrıştırmak için hangi üretimin izleneceğini belirleyemez. Bu karışıklığı gidermek için sol çarpanlara ayırma adı verilen bir teknik kullanıyoruz.

Sol faktörleme, dilbilgisini yukarıdan aşağıya ayrıştırıcılar için kullanışlı hale getirmek üzere dönüştürür. Bu teknikte, her ortak önek için bir üretim yapıyoruz ve türetmenin geri kalanı yeni üretimlerle ekleniyor.

Example

Yukarıdaki üretimler şu şekilde yazılabilir:

A => αA'
A'=> β |  | …

Artık ayrıştırıcının önek başına yalnızca bir üretimi vardır ve bu da karar almayı kolaylaştırır.

İlk ve Takip Setleri

Ayrıştırıcı tablosu yapısının önemli bir parçası, ilk ve takip eden kümeleri oluşturmaktır. Bu kümeler, türetmedeki herhangi bir terminalin gerçek konumunu sağlayabilir. Bu, T [A, t] = α'yı bazı üretim kurallarıyla değiştirme kararının bulunduğu ayrıştırma tablosunu oluşturmak için yapılır.

İlk Set

Bu küme, ilk pozisyonda bir terminal olmayan tarafından hangi terminal sembolünün türetildiğini bilmek için oluşturulur. Örneğin,

α → t β

Yani α, t'yi (terminal) ilk pozisyonda türetir. Öyleyse, t ∈ İLK (α).

İlk seti hesaplamak için algoritma

İLK (α) kümesinin tanımına bakın:

α bir terminal ise, İLK (α) = {α}.
α terminal olmayan ve α → ℇ bir üretim ise, İLK (α) = {ℇ}.
α bir terminal değilse ve α → 1 2 3… n ve herhangi bir FIRST () t içeriyorsa, o zaman t İLK (α) dır.

İlk set şu şekilde görülebilir:

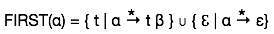
Seti Takip Et

Benzer şekilde, üretim kurallarında hangi terminal sembolünün terminal olmayan bir α'yı hemen takip ettiğini hesaplıyoruz. Terminal olmayanın ne üretebileceğini düşünmüyoruz, bunun yerine terminal olmayanın üretimlerini izleyen bir sonraki terminal sembolünün ne olacağını görüyoruz.

Takip setini hesaplamak için algoritma:

α bir başlangıç sembolü ise, TAKİP () = $
α terminal dışı ise ve α → AB üretimine sahipse, FIRST (B), ℇ hariç FOLLOW (A) 'dadır.
α bir terminal değilse ve bir α → AB üretimine sahipse, burada B ℇ ise, TAKİP (A) TAKİP (α) 'dır.

Takip kümesi şu şekilde görülebilir: TAKİP (α) = {t | S * αt *}

Sözdizimi Çözümleyicilerinin Sınırlamaları

Sözdizimi çözümleyicileri, girdilerini sözcüksel çözümleyicilerden simge biçiminde alır. Sözcüksel çözümleyiciler, sözdizimi çözümleyicisi tarafından sağlanan bir belirtecin geçerliliğinden sorumludur. Sözdizimi çözümleyicileri aşağıdaki dezavantajlara sahiptir -

bir belirtecin geçerli olup olmadığını belirleyemez,
bir belirtecin kullanılmadan önce bildirilip bildirilmediğini belirleyemez,
bir belirtecin kullanılmadan önce başlatılıp başlatılmadığını belirleyemez,
bir belirteç türü üzerinde gerçekleştirilen bir işlemin geçerli olup olmadığını belirleyemez.

Bu görevler, Anlamsal Analiz'de çalışacağımız anlamsal analizci tarafından gerçekleştirilir.