Derleyici Tasarımı - Yukarıdan Aşağıya Ayrıştırıcı

Son bölümde, yukarıdan aşağıya ayrıştırma tekniğinin girdiyi ayrıştırdığını ve kök düğümden yavaş yavaş yaprak düğümlerine inen bir ayrıştırma ağacı oluşturmaya başladığını öğrendik. Yukarıdan aşağıya ayrıştırma türleri aşağıda gösterilmiştir:

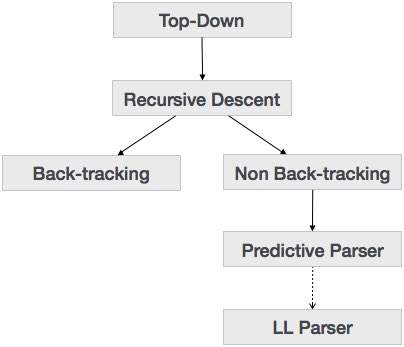
Yinelemeli Alçalma Ayrıştırma

Özyinelemeli iniş, ayrıştırma ağacını üstten inşa eden ve giriş soldan sağa doğru okunan yukarıdan aşağıya bir ayrıştırma tekniğidir. Her terminal ve terminal olmayan varlık için prosedürleri kullanır. Bu ayrıştırma tekniği, geri izleme gerektirebilen veya gerektirmeyen bir ayrıştırma ağacı yapmak için girdiyi özyinelemeli olarak ayrıştırır. Ancak onunla ilişkili dilbilgisi (faktörlü bırakılmamışsa) geriye dönük takipten kaçınamaz. Geri izleme gerektirmeyen bir özyinelemeli-iniş ayrıştırma biçimi olarak bilinirpredictive parsing.

Bu ayrıştırma tekniği, doğası gereği özyinelemeli bağlamdan bağımsız dilbilgisi kullandığı için özyinelemeli olarak kabul edilir.

Geri izleme

Yukarıdan aşağı ayrıştırıcılar, kök düğümden (başlangıç ​​sembolü) başlar ve giriş dizesini, bunları değiştirmek için üretim kurallarına göre eşleştirir (eşleşirse). Bunu anlamak için aşağıdaki CFG örneğini ele alalım:

S → rXd | rZd
X → oa | ea
Z → ai

Bir girdi dizesi için: yukarıdan aşağıya bir ayrıştırıcı olan read (read) şu şekilde davranacaktır:

Üretim kurallarından S ile başlayacak ve verimini girdinin en soldaki harfiyle, yani 'r' ile eşleştirecektir. S (S → rXd) 'nin üretimi onunla eşleşir. Böylece yukarıdan aşağıya ayrıştırıcı bir sonraki giriş harfine (yani 'e') ilerler. Ayrıştırıcı, terminal olmayan 'X'i genişletmeye çalışır ve üretimini soldan kontrol eder (X → oa). Bir sonraki giriş sembolü ile uyuşmuyor. Dolayısıyla yukarıdan aşağıya ayrıştırıcı, X'in bir sonraki üretim kuralını (X → ea) elde etmek için geriye doğru izler.

Şimdi ayrıştırıcı, tüm giriş harflerini sıralı bir şekilde eşleştirir. Dize kabul edilir.

Tahmine Dayalı Ayrıştırıcı

Öngörülü ayrıştırıcı, girdi dizesini değiştirmek için hangi üretimin kullanılacağını tahmin etme yeteneğine sahip özyinelemeli bir iniş ayrıştırıcısıdır. Öngörülü ayrıştırıcı, geri izleme sorunu yaşamaz.

Tahmine dayalı ayrıştırıcı, görevlerini yerine getirmek için, sonraki giriş sembollerini gösteren ileriye dönük bir işaretçi kullanır. Ayrıştırıcıyı geri izlemesiz yapmak için, öngörücü ayrıştırıcı dilbilgisine bazı kısıtlamalar getirir ve yalnızca LL (k) dilbilgisi olarak bilinen bir gramer sınıfını kabul eder.

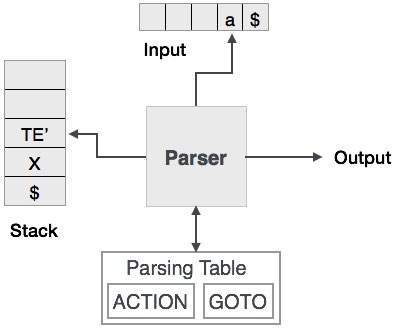
Öngörülü ayrıştırma, girdiyi ayrıştırmak ve bir ayrıştırma ağacı oluşturmak için bir yığın ve ayrıştırma tablosu kullanır. Hem yığın hem de giriş bir bitiş sembolü içerir$yığının boş olduğunu ve girdinin tüketildiğini belirtmek için. Ayrıştırıcı, girdi ve yığın elemanı kombinasyonu hakkında herhangi bir karar almak için ayrıştırma tablosuna başvurur.

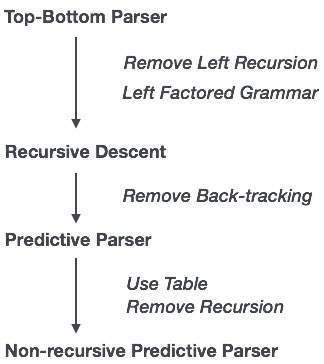
Özyinelemeli iniş ayrıştırmada, ayrıştırıcı, tek bir girdi örneği için seçilebilecek birden fazla üretime sahip olabilir, oysa tahmini ayrıştırıcıda, her adımın seçilecek en fazla bir üretimi vardır. Giriş dizesiyle eşleşen üretimin olmadığı durumlar olabilir ve bu da ayrıştırma prosedürünün başarısız olmasına neden olur.

LL Ayrıştırıcı

LL Parser LL dilbilgisini kabul eder. LL dilbilgisi, bağlamdan bağımsız dilbilgisinin bir alt kümesidir, ancak kolay uygulama sağlamak için basitleştirilmiş sürümü almak için bazı kısıtlamalar vardır. LL dilbilgisi, her iki algoritma, yani özyinelemeli-iniş veya tablo tabanlı olarak uygulanabilir.

LL ayrıştırıcısı, LL (k) olarak belirtilir. LL (k) 'deki ilk L, girdiyi soldan sağa ayrıştırır, LL (k)' deki ikinci L, en soldaki türetme anlamına gelir ve k'nin kendisi, önden bakma sayısını temsil eder. Genel olarak k = 1 olduğundan LL (k) LL (1) olarak da yazılabilir.

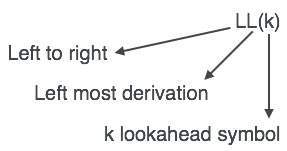
LL Ayrıştırma Algoritması

Tablonun boyutu k değeri ile üssel olarak büyüdüğünden, ayrıştırıcı açıklaması için deterministik LL (1) 'e sadık kalabiliriz. İkinci olarak, belirli bir gramer LL (1) değilse, o zaman genellikle, verilen herhangi bir k için LL (k) değildir.

Aşağıda, LL (1) Ayrıştırma için bir algoritma verilmiştir:

Input: 
   string ω 
   parsing table M for grammar G

Output:
   If ω is in L(G) then left-most derivation of ω,
   error otherwise.

Initial State : $S on stack (with S being start symbol)
   ω$ in the input buffer

SET ip to point the first symbol of ω$.

repeat
   let X be the top stack symbol and a the symbol pointed by ip.

   if X∈ Vt or $
      if X = a
         POP X and advance ip.
      else
         error()
      endif
      
   else	/* X is non-terminal */
      if M[X,a] = X → Y1, Y2,... Yk    
         POP X
         PUSH Yk, Yk-1,... Y1 /* Y1 on top */
         Output the production X → Y1, Y2,... Yk 
      else
         error()
      endif
   endif
until X = $	/* empty stack */

Bir gramer G, LL (1), eğer A → α | β G'nin iki farklı ürünüdür:

• terminal yok için, hem α hem de a, a ile başlayan dizeleri türetir.

• en fazla α ve β'den biri boş dizge türetebilir.

• β → t ise, α TAKİP (A) 'da bir uçbirimle başlayan herhangi bir dizge türetmez.