Veri Yapısı ve Algoritmalar - AVL Trees

İkili arama ağacının girdisi sıralı (artan veya azalan) bir şekilde gelirse ne olur? Daha sonra şöyle görünecek -

BST'nin en kötü durum performansının doğrusal arama algoritmalarına en yakın, yani Ο (n) olduğu görülmektedir. Gerçek zamanlı verilerde, veri modelini ve frekanslarını tahmin edemeyiz. Dolayısıyla, mevcut BST'yi dengeleme ihtiyacı ortaya çıkıyor.

Mucitlerinden sonra adlandırıldı Adelson, Velski & Landis, AVL treesyükseklik dengeleme ikili arama ağacıdır. AVL ağacı, sol ve sağ alt ağaçların yüksekliğini kontrol eder ve farkın 1'den fazla olmamasını sağlar. Bu farkaBalance Factor.

Burada ilk ağacın dengeli olduğunu ve sonraki iki ağacın dengeli olmadığını görüyoruz -

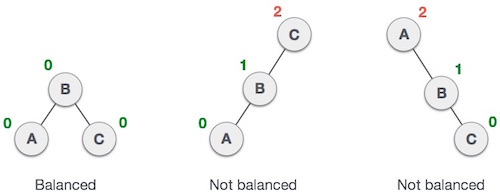
İkinci ağaçta sol alt ağaç C yüksekliği 2'dir ve sağ alt ağacın yüksekliği 0'dır, dolayısıyla fark 2'dir. Üçüncü ağaçta, Ayüksekliği 2 ve sol eksik, yani 0 ve fark yine 2. AVL ağacı, farkın (denge faktörü) yalnızca 1 olmasına izin verir.

BalanceFactor = height(left-sutree) − height(right-sutree)

Sol ve sağ alt ağaçların yükseklik farkı 1'den fazla ise ağaç bazı döndürme teknikleri kullanılarak dengelenir.

AVL Rotasyonları

Kendini dengelemek için, bir AVL ağacı aşağıdaki dört tür dönüşü gerçekleştirebilir -

• Sola dönüş
• Sağa dönüş
• Sol-Sağ dönüş
• Sağa-Sola dönüş

İlk iki rotasyon tek rotasyondur ve sonraki iki rotasyon çift rotasyondur. Dengesiz bir ağaca sahip olmak için en azından 2 boyunda bir ağaca ihtiyacımız var. Bu basit ağaçla onları tek tek anlayalım.

Sol Dönüş

Bir ağaç dengesiz hale gelirse, sağ alt ağacın sağ alt ağacına bir düğüm eklendiğinde, o zaman tek bir sola dönüş gerçekleştiririz -

Örneğimizde düğüm AA'nın sağ alt ağacının sağ alt ağacına bir düğüm eklendiğinde dengesiz hale geldi. Sol dönüşü yaparakA B'nin sol alt ağacı

Sağa Dönüş

Sol alt ağacın sol alt ağacına bir düğüm eklenirse, AVL ağacı dengesiz hale gelebilir. Ağacın daha sonra doğru bir dönüşe ihtiyacı vardır.

Gösterildiği gibi, dengesiz düğüm, bir sağa dönüş yaparak sol çocuğunun sağ çocuğu olur.

Sol-Sağ Döndürme

Çift rotasyonlar, önceden açıklanan rotasyon versiyonlarının biraz karmaşık versiyonlarıdır. Bunları daha iyi anlamak için rotasyon sırasında gerçekleştirilen her eylemi not almalıyız. Önce Sol-Sağ dönüşü nasıl gerçekleştireceğimizi kontrol edelim. Sola-sağa dönüş, sola dönüşün ardından sağa dönüşün bir kombinasyonudur.

Durum	Aksiyon
	Sol alt ağacın sağ alt ağacına bir düğüm eklendi. Bu yaparCdengesiz bir düğüm. Bu senaryolar AVL ağacının sola-sağa dönüş yapmasına neden olur.
	Önce sol alt ağacında sol dönüşü gerçekleştiriyoruz C. Bu yaparA, sol alt ağacı B.
	Düğüm C hala dengesiz, ancak şimdi bunun nedeni sol alt ağacın sol alt ağacından kaynaklanıyor.
	Şimdi ağacı sağa çevireceğiz B bu alt ağacın yeni kök düğümü. C şimdi kendi sol alt ağacının sağ alt ağacı olur.
	Ağaç artık dengelenmiştir.

Sağ-Sol Döndürme

İkinci tür çift dönüş Sağ-Sol Dönüştür. Sağa dönüşün ardından sola dönüşün bir kombinasyonudur.

Durum	Aksiyon
	Sağ alt ağacın sol alt ağacına bir düğüm eklendi. Bu yaparA, denge faktörü 2 olan dengesiz bir düğüm.
	İlk olarak, doğru dönüşü gerçekleştiriyoruz C düğüm, yapma C kendi sol alt ağacının sağ alt ağacı B. Şimdi,B sağ alt ağacı olur A.
	Düğüm A sağ alt ağacının sağ alt ağacı nedeniyle hala dengesizdir ve sola dönüş gerektirir.
	Yapılarak bir sola dönüş gerçekleştirilir B alt ağacın yeni kök düğümü. A sağ alt ağacının sol alt ağacı olur B.
	Ağaç artık dengelenmiştir.