DAA - Optimal Birleştirme Modeli
Farklı uzunluktaki bir dizi sıralı dosyayı tek bir sıralı dosyada birleştirin. Ortaya çıkan dosyanın minimum sürede oluşturulacağı optimum bir çözüm bulmamız gerekiyor.
Sıralanan dosyaların sayısı belirtilmişse, bunları tek bir sıralı dosyada birleştirmenin birçok yolu vardır. Bu birleştirme çiftler halinde yapılabilir. Bu nedenle, bu tür bir birleştirme,2-way merge patterns.
Farklı eşlemeler farklı miktarlarda zaman gerektirdiğinden, bu stratejide birçok dosyayı bir araya getirmenin en uygun yolunu belirlemek istiyoruz. Her adımda, en kısa iki dizi birleştirilir.
Birleştirmek için p-record file ve bir q-record file muhtemelen gerektirir p + q kayıt hareketleri, bariz seçim, her adımda en küçük iki dosyayı birleştirmektir.
İki yönlü birleştirme desenleri, ikili birleştirme ağaçları ile temsil edilebilir. Bir dizi düşünelimn sıralı dosyalar {f1, f2, f3, …, fn}. Başlangıçta, bunun her bir öğesi tek düğümlü ikili ağaç olarak kabul edilir. Bu en uygun çözümü bulmak için aşağıdaki algoritma kullanılır.
Algorithm: TREE (n)
for i := 1 to n – 1 do
declare new node
node.leftchild := least (list)
node.rightchild := least (list)
node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight)
insert (list, node);
return least (list);Bu algoritmanın sonunda, kök düğümün ağırlığı optimum maliyeti temsil eder.
Misal
Sırasıyla 20, 30, 10, 5 ve 30 elemanlı verilen f 1 , f 2 , f 3 , f 4 ve f 5 dosyalarını ele alalım .
Birleştirme işlemleri sağlanan sıraya göre gerçekleştirilirse,
M1 = merge f1 and f2 => 20 + 30 = 50
M2 = merge M1 and f3 => 50 + 10 = 60
M3 = merge M2 and f4 => 60 + 5 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Dolayısıyla, toplam işlem sayısı
50 + 60 + 65 + 95 = 270
Şimdi, soru ortaya çıkıyor daha iyi bir çözüm var mı?
Sayıları boyutlarına göre artan sırada sıralayarak aşağıdaki sırayı elde ederiz -
f4, f3, f1, f2, f5
Bu nedenle, birleştirme işlemleri bu sıra üzerinde gerçekleştirilebilir
M1 = merge f4 and f3 => 5 + 10 = 15
M2 = merge M1 and f1 => 15 + 20 = 35
M3 = merge M2 and f2 => 35 + 30 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Bu nedenle, toplam işlem sayısı
15 + 35 + 65 + 95 = 210
Açıkçası, bu öncekinden daha iyi.
Bu bağlamda, şimdi bu algoritmayı kullanarak sorunu çözeceğiz.
İlk Set

Aşama 1
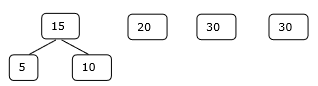
Adım 2
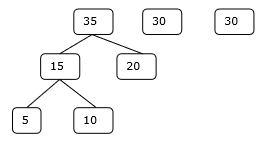
Aşama 3
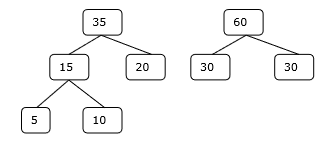
4.Adım
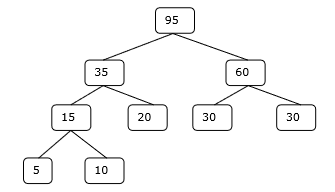
Dolayısıyla, çözüm 15 + 35 + 60 + 95 = 205 sayıda karşılaştırma gerektirir.