Günlük ve Anti Log Amplifikatörleri
Logaritma ve anti-logaritma (üstel) gibi matematiksel işlemleri bir amplifikasyonla gerçekleştiren elektronik devrelere denir. Logarithmic amplifier ve Anti-Logarithmic amplifier sırasıyla.
Bu bölüm aşağıdakileri tartışır: Logarithmic amplifier ve Anti-Logarithmic amplifierdetayda. Lütfen bu amplifikatörlerin doğrusal olmayan uygulamalar kapsamına girdiğini unutmayın.
Logaritmik Amplifikatör
Bir logarithmic amplifierveya a log amplifier, uygulanan girişin logaritması ile orantılı bir çıktı üreten elektronik bir devredir. Bu bölümde op-amp tabanlı logaritmik amplifikatör ayrıntılı olarak tartışılmaktadır.
Op-amp tabanlı bir logaritmik amplifikatör, çıkışta, ters çevirme terminaline bağlı dirence uygulanan voltajın logaritması ile orantılı olan bir voltaj üretir. circuit diagram op-amp tabanlı bir logaritmik amplifikatörün, aşağıdaki şekilde gösterilmektedir -
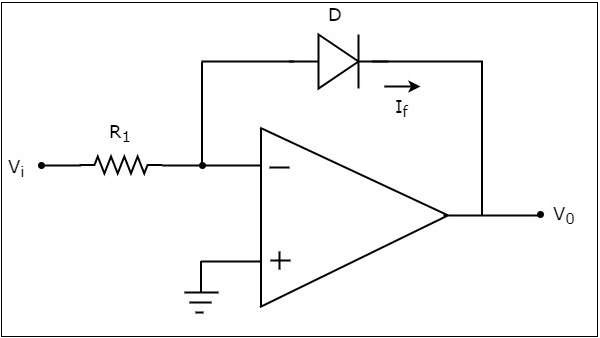
Yukarıdaki devrede, op-amp'in ters çevirmeyen giriş terminali toprağa bağlanır. Bu, op-amp'in ters çevirmeyen giriş terminaline sıfır volt uygulandığı anlamına gelir.
Göre virtual short conceptbir op-amp'in ters çeviren giriş terminalindeki voltaj, tersine çevirmeyen giriş terminalindeki voltaja eşit olacaktır. Yani, ters çevirme giriş terminalindeki voltaj sıfır volt olacaktır.
nodal equation ters çeviren giriş terminalinin düğümünde -
$$ \ frac {0-V_i} {R_1} + I_ {f} = 0 $$
$$ => I_ {f} = \ frac {V_i} {R_1} ...... Denklem 1 $$
Aşağıdaki equation for current ileri önyargılı olduğunda bir diyot içinden akan -
$$ I_ {f} = I_ {s} e ^ {(\ frac {V_f} {nV_T})} ...... Denklem 2 $$
nerede,
$ I_ {s} $ diyotun doygunluk akımıdır,
$ V_ {f} $, ileri önyargılı olduğunda diyot boyunca voltaj düşüşüdür,
$ V_ {T} $, diyotun termal eşdeğer voltajıdır.
KVL equation op amplifikatörün geri bildirim döngüsü etrafında -
$$ 0-V_ {f} -V_ {0} = 0 $$
$$ => V_ {f} = - V_ {0} $$
Denklem 2'deki $ V_ {f} $ değerini değiştirerek şunu elde ederiz -
$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ sağ)} ...... Denklem 3 $$
Hem denklem 1 hem de denklem 3'ün sol taraftaki terimlerinin aynı olduğunu gözlemleyin. Bu nedenle, bu iki denklemin sağ taraftaki terimini aşağıda gösterildiği gibi eşitleyin -
$$ \ frac {V_i} {R_1} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ sağ)} $$
$$ \ frac {V_i} {R_1I_s} = e ^ {\ left (\ frac {-V_0} {nV_T} \ sağ)} $$
Uygulanıyor natural logarithm her iki tarafta da -
$$ In \ left (\ frac {V_i} {R_1I_s} \ right) = \ frac {-V_0} {nV_T} $$
$$ V_ {0} = - {nV_T} İç \ sol (\ frac {V_i} {R_1I_s} \ sağ) $$
Yukarıdaki denklemde n, $ {V_T} $ ve $ I_ {s} $ parametrelerinin sabit olduğuna dikkat edin. Dolayısıyla, $ V_ {0} $ çıkış voltajı ile orantılı olacaktır.natural logarithm $ R_ {1} $ direnç değerinin sabit bir değeri için $ V_ {i} $ giriş geriliminin değeri.
Bu nedenle, yukarıda tartışılan op-amp tabanlı logaritmik amplifikatör devresi, $ {R_1I_s} = 1V $ olduğunda, $ {V_T} $ giriş voltajının doğal logaritması ile orantılı bir çıktı üretecektir.
$ V_ {0} $ çıkış voltajının bir negative signgiriş ve çıkış arasında 180 0 faz farkı olduğunu gösterir .
Anti-Logaritmik Amplifikatör
Bir anti-logarithmic amplifierveya bir anti-log amplifier, uygulanan girişin anti-logaritması ile orantılı bir çıktı üreten elektronik bir devredir. Bu bölümde op-amp tabanlı anti-logaritmik amplifikatör ayrıntılı olarak tartışılmaktadır.
Op-amp tabanlı bir anti-logaritmik amplifikatör, çıkışta, ters çevirme terminaline bağlı diyota uygulanan voltajın anti-logaritması ile orantılı olan bir voltaj üretir.
circuit diagram op-amp tabanlı bir anti-logaritmik amplifikatörün örnekleri aşağıdaki şekilde gösterilmektedir -

Yukarıda gösterilen devrede, op-amp'in ters çevirmeyen giriş terminali toprağa bağlanır. Tersine çevirmeyen giriş terminaline sıfır volt uygulandığı anlamına gelir.
Göre virtual short conceptop-amp'in ters çeviren giriş terminalindeki voltaj, tersine çevirmeyen giriş terminalinde bulunan voltaja eşit olacaktır. Dolayısıyla, ters çeviren giriş terminalindeki voltaj sıfır volt olacaktır.
nodal equation ters çeviren giriş terminalinin düğümünde -
$$ - I_ {f} + \ frac {0-V_0} {R_f} = 0 $$
$$ => - \ frac {V_0} {R_f} = I_ {f} $$
$$ => V_ {0} = - R_ {f} I_ {f} ......... Denklem 4 $$
Bir diyottan akan akımın denkleminin ileri taraflıyken aşağıda verildiği gibi olduğunu biliyoruz -
$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ sağ)} $$
Denklem 4'teki $ I_ {f} $ değerini değiştirerek şunu elde ederiz:
$$ V_ {0} = - R_ {f} \ sol \ {{I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ sağ)}} \ sağ \} $$
$$ V_ {0} = - R_ {f} {I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ sağ)}} ...... Denklem 5 $$
Op amp'in ters çevirme terminalinin giriş tarafındaki KVL denklemi
$$ V_ {i} -V_ {f} = 0 $$
$$ V_ {f} = V_ {i} $$
Denklem 5'teki değeri yerine koyarsak -
$$ V_ {0} = - R_ {f} {I_ {s} e ^ {\ left (\ frac {V_i} {nV_T} \ sağ)}} $$
Yukarıdaki denklemde n, $ {V_T} $ ve $ I_ {s} $ parametrelerinin sabit olduğuna dikkat edin. Dolayısıyla, $ {V_0} $ çıkış voltajı ile orantılı olacaktır.anti-natural logarithm $ {R_f} $ geri besleme direncinin sabit bir değeri için $ {V_i} $ giriş geriliminin (üstel)
Bu nedenle, yukarıda tartışılan op-amp tabanlı anti-logaritmik amplifikatör devresi, $ {V_i} $ zaman, $ {R_fI_s} = 1V $ giriş voltajının doğal olmayan logaritması (üstel) ile orantılı bir çıktı üretecektir. $ {V_0} $ çıkış voltajının birnegative signgiriş ve çıkış arasında 180 0 faz farkı olduğunu gösterir .