Küresel Aynaların Oluşturduğu Görüntüler
Giriş
Işın diyagramlarını çizmek, görüntülerin oluşumunu küresel aynalarla göstermenin ideal bir yoludur.
En az iki yansıyan ışının kesişimi, nokta nesnenin doğru imaj konumunu verir.
Aşağıdaki tablo, bir concave mirror verilen nesnenin farklı konumları için -
| Nesnenin Konumu | Görüntünün Konumu | Resmin Boyutu | Görüntünün Doğası | Resim |
|---|---|---|---|---|
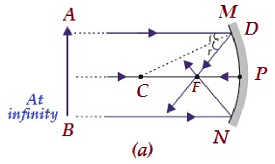
| Sonsuzda | Odakta F | Son derece küçültülmüş, poinbeded | Gerçek ve ters |
|
| C'nin ötesinde | S / B F ve C | Azaldı | Gerçek ve ters |

|
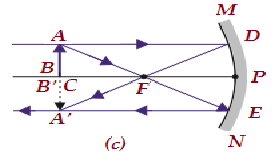
| C'de | C'de | Aynı boyutta | Gerçek ve ters |
|
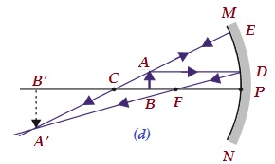
| S / B C ve F | C'nin ötesinde | Büyütülmüş | Gerçek ve ters |
|
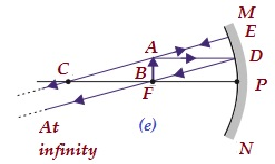
| F'de | Sonsuzda | Son derece büyüt | Gerçek ve ters |
|
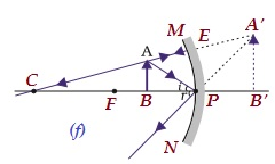
| S / B P ve F | Aynanın arkasında | Büyütülmüş | Sanal ve dik |
|
İçbükey Aynanın Kullanımları
Güçlü paralel ışık demetleri elde etmek için içbükey aynalar evrensel olarak meşaleler, arama lambaları ve araç farlarında kullanılır.
İçbükey ayna daha geniş görüş sağladığından berber salonunda da kullanılmaktadır.
İçbükey ayna, diş hekimleri tarafından hastaların dişlerinin büyük görüntülerini görmek için de kullanılmaktadır.
Güneş fırınlarında maksimum ısı üretmek için güneş ışığını yoğunlaştırmak için büyük içbükey aynalar kullanılır.
Dışbükey Ayna ile görüntü oluşumu
Aşağıdaki tablo, bir concave mirror verilen nesnenin farklı konumları için -
| Nesnenin Konumu | Görüntünün Konumu | Resmin Boyutu | Görüntünün Doğası | Resim |
|---|---|---|---|---|
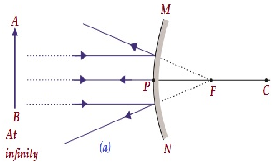
| Sonsuzda | F odak noktasında, aynanın arkasında | Büyük ölçüde küçültülmüş, nokta boyutunda | Sanal ve dik |
|
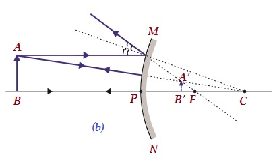
| S / b sonsuzluk ve aynanın kutbu | S / B P ve F, aynanın arkasında | Diminishe d | Sanal ve dik |
|
Dışbükey Aynaların Kullanım Alanları
Tüm araçlarda dışbükey aynalar evrensel olarak dikiz aynası (kanat) olarak kullanılır.
Araçlarda küçülse de dik bir görüntü verdikleri için dışbükey aynalar tercih edilir.
Ayna Formülü
Formül şu şekilde ifade edilir:
Ayna formülü, nesne-uzaklık arasındaki ilişkileri ifade eder (ör. u), görüntü mesafesi (yani v) ve küresel bir aynanın odak uzaklığı (yani f).
$$ \ frac {1} {v} + \ frac {1} {u} = \ frac {1} {f} $$