Uydu Haberleşmesi - Yörünge Mekaniği

Dünyanın etrafında dönen uydunun yolunun şu adla bilindiğini biliyoruz: orbit. Bu yol matematiksel gösterimle gösterilebilir. Yörünge mekaniği, yörüngelerde bulunan uyduların hareketinin incelenmesidir. Böylece yörünge hareketi bilgisi ile uzay işlemlerini rahatlıkla anlayabiliriz.

Yörünge Elemanları

Yörünge unsurları, uyduların yörünge hareketini tanımlamaya yardımcı olan parametrelerdir. Aşağıdakilerorbital elements.

Yarı büyük eksen
Eccentricity
Ortalama anormallik
Perigee argümanı
Inclination
Yükselen düğümün sağ yükselişi

Yukarıdaki altı yörünge öğesi, dünya uydularının yörüngesini tanımlar. Bu nedenle, yörünge elemanlarının değerlerine göre bir uyduyu diğer uydulardan ayırt etmek kolaydır.

Yarı büyük eksen

Uzunluğu Semi-major axis (a)Uydunun yörüngesinin boyutunu tanımlar. Ana eksenin yarısıdır. Bu merkezden elipsin kenarına odaklanır. Yani, yörüngenin en uzak iki noktasındaki bir yörüngenin yarıçapıdır.

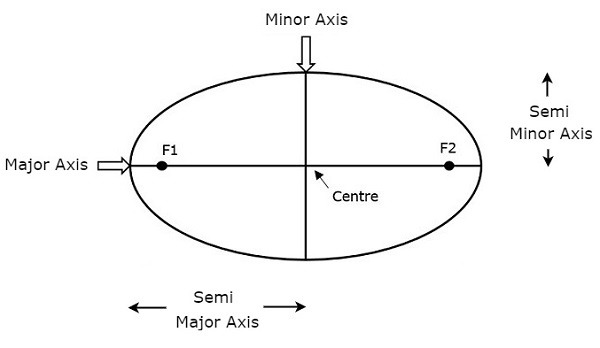
Hem yarı büyük eksen hem de yarı küçük eksen yukarıdaki şekilde gösterilmektedir. Yarı uzunlukmajor axis (a) sadece uydunun yörüngesinin boyutunu değil, aynı zamanda devrimin zaman dilimini de belirler.

Dairesel yörünge özel bir durum olarak kabul edilirse, yarı büyük eksenin uzunluğu eşit olacaktır. radius bu dairesel yörüngenin.

Eksantriklik

Değeri Eccentricity (e)uydunun yörüngesinin şeklini düzeltir. Bu parametre, yörünge şeklinin mükemmel bir daireden sapmasını gösterir.

Eliptik bir yörüngenin yarı büyük eksen ve yarı küçük eksen uzunlukları a & b ise, matematiksel ifade eccentricity (e) olacak

$$e = \frac{\sqrt{a^2 - b^2}}{a}$$

Dairesel bir yörüngenin eksantrikliğinin değeri zero, çünkü hem a hem de b eşittir. Oysa eliptik bir yörüngenin eksantrikliğinin değeri sıfır ile bir arasındadır.

Aşağıdaki figure farklı eksantriklik (e) değerleri için çeşitli uydu yörüngelerini gösterir

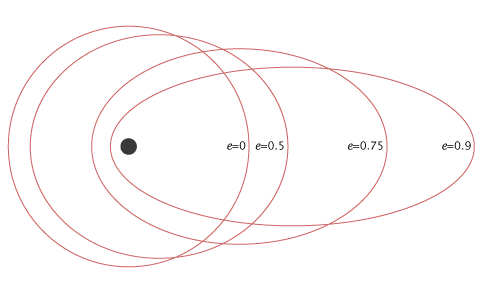
Yukarıdaki şekilde, sıfırın eksantriklik (e) değerine karşılık gelen uydu yörüngesi, dairesel bir yörüngedir. Ve kalan üç uydu yörüngesi, 0.5, 0.75 ve 0.9 eksantriklik (e) değerlerine karşılık gelen eliptiktir.

Ortalama Anomali

Bir uydu için Dünya'ya en yakın olan nokta Perigee olarak bilinir. Mean anomaly (M), perige ile ilgili olarak uydunun açısal konumunun ortalama değerini verir.

Yörünge daireselse, Ortalama anormallik uydunun yörüngedeki açısal konumunu verir. Ancak yörünge eliptik ise, kesin konumun hesaplanması çok zordur. O sırada, ortalama anormallik bir ara adım olarak kullanılır.

Perigee Argümanı

Uydu yörüngesi, ekvator düzlemini iki noktadan keser. İlk nokta olarak adlandırılırdescending nodeuydunun kuzey yarımküreden güney yarımküreye geçtiği yer. İkinci nokta olarak adlandırılırascending nodeuydunun güney yarımküreden kuzey yarımküreye geçtiği yer.

Argument of perigee (ω)yükselen düğüm ve perigee arasındaki açıdır. Hem perigee hem de artan düğüm aynı noktada mevcutsa, perigee argümanı sıfır derece olacaktır.

Perigee argümanı, uydu hareketi yönünde dünyanın merkezinde yörünge düzleminde ölçülür.

Eğim

Yörünge düzlemi ile dünyanın ekvator düzlemi arasındaki açı olarak bilinir inclination (i). Doğudan kuzeye yön ile yükselen düğümde ölçülür. Dolayısıyla eğim, dünyanın ekvatorunu referans alarak yörüngenin yönünü tanımlar.

Eğim açısına göre dört tür yörünge vardır.

Equatorial orbit - Eğim açısı sıfır derece veya 180 derecedir.
Polar orbit - Eğim açısı 90 derecedir.
Prograde orbit - Eğim açısı sıfır ile 90 derece arasındadır.
Retrograde orbit - Eğim açısı 90 ile 180 derece arasındadır.

Yükselen düğümün Sağ Açıklığı

Biz biliyoruz ki ascending node uydunun güney yarımküreden kuzey yarımküreye giderken ekvator düzlemini geçtiği noktadır.

Yükselen düğümün Sağ Yükselişi (Ω)Koç çizgisi ile ekvator düzleminde doğu yönüne doğru yükselen düğüm arasındaki açıdır. Koç, aynı zamanda vernal ve ekinoks olarak da adlandırılır.

Uydu ground tracktam yörüngesinin altında yer alan Dünya yüzeyindeki yoldur. Bir uydunun yer rotası, yörünge elemanlarının değerlerine bağlı olarak bir dizi farklı biçim alabilir.

Orbital Denklemler

Bu bölümde yörünge hareketiyle ilgili denklemleri tartışalım.

Uyduya etki eden kuvvetler

Bir uydu, dünyanın etrafında döndüğünde, dünyanın çekim kuvveti nedeniyle dünyadan bir çekme kuvvetine maruz kalır. Bu kuvvet olarak bilinirCentripetal force(F ₁ ) çünkü bu kuvvet uyduyu ona doğru yöneltir.

Matematiksel olarak Centripetal force(F ₁ ) yeryüzü nedeniyle uyduya etki eden şu şekilde yazılabilir:

$$F_{1} = \frac{GMm}{R^2} $$

Nerede,

Gevrensel yerçekimi sabitidir ve 6.673 x ^10-11 N ∙ m ² / kg ^2'ye eşittir .
Mdünyanın kütlesi olup 5.98 x 10 ²⁴ Kg'ye eşittir .
m uydunun kütlesidir.
R uydudan Dünya'nın merkezine olan mesafedir.

Bir uydu, dünyanın etrafında döndüğünde, yerçekimi kuvvetleri nedeniyle güneşten ve aydan bir çekme kuvvetine maruz kalır. Bu kuvvet olarak bilinirCentrifugal force(F ₂ ) çünkü bu kuvvet uyduyu dünyadan uzaklaştırır.

Matematiksel olarak Centrifugal force(F ₂ ) uydu üzerinde hareket eden şu şekilde yazılabilir:

$$F_{2} = \frac{mv^2}{R} $$

Nerede, v uydunun yörünge hızıdır.

Yörünge Hızı

Uydunun yörünge hızı, uydunun dünya etrafında döndüğü hızdır. Uydu yörüngesinden sapmaz ve hem Merkezcil hem de Merkezkaç kuvvetleri olduğunda bu yörüngede belirli bir hızla hareket eder.balance herbiri.

Yani, equateMerkezcil kuvvet (F ₁ ) ve Merkezkaç kuvveti (F ₂ ).

$$\frac{GMm}{R^2} = \frac{mv^2}{R}$$

$$= > \frac{GM}{R} = v^2$$

$$= > v = \sqrt{\frac{GM}{R}}$$

bu yüzden orbital velocity uydunun

$$v = \sqrt{\frac{GM}{R}}$$

Nerede,