Điện tử cơ bản - Điện cảm
Thuộc tính của một cuộn cảm để có được điện áp gây ra bởi sự thay đổi của dòng điện, được định nghĩa là Điện cảm. Độ tự cảm là tỷ số giữa hiệu điện thế và tốc độ thay đổi của dòng điện.
Tốc độ thay đổi của dòng điện tạo ra sự thay đổi trong từ trường, tạo ra EMF ngược hướng với nguồn điện áp. Tính chất cảm ứng EMF này được gọi làInductance.
Công thức cho độ tự cảm là
$$ Điện cảm \: \: = \: \: \ frac {volatge} {rate \: of \: change \: of \: current} $$
Units −
Đơn vị của điện cảm là Henry. Nó được chỉ ra bởiL.
Các cuộn cảm chủ yếu có sẵn ở dạng mH (mili Henry) và μH (micro Henry).
Một cuộn dây được cho là có độ tự cảm là one Henry khi EMF của one volt là hiện tượng tự cảm trong cuộn dây mà dòng điện chạy qua thay đổi với tốc độ one ampere per second.
Tự cảm
Nếu một cuộn dây được coi là trong đó một số dòng điện chạy qua, thì nó có một số từ trường, vuông góc với dòng điện. Khi dòng điện này tiếp tục thay đổi, từ trường cũng thay đổi và từ trường thay đổi này, tạo ra EMF, ngược chiều với điện áp nguồn. EMF đối lập này được tạo ra làself-induced voltage và phương pháp này được gọi là self-inductance.
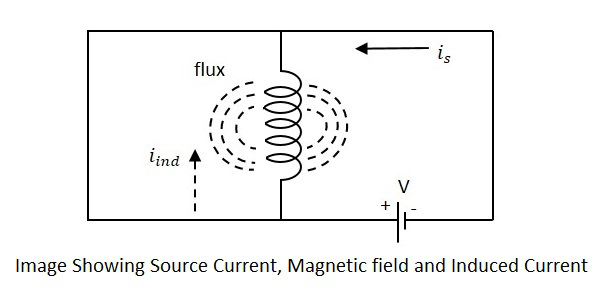
Hiện tại is trong hình chỉ ra nguồn hiện tại trong khi iindcho biết cường độ dòng điện cảm ứng. Từ thông biểu thị từ thông tạo ra xung quanh cuộn dây. Với ứng dụng của điện áp, dòng điệniscác dòng chảy và thông lượng được tạo ra. Khi hiện tạiis khác nhau, thông lượng được sản xuất khác nhau iind.
EMF cảm ứng này qua cuộn dây tỷ lệ với tốc độ thay đổi dòng điện. Tốc độ thay đổi dòng điện càng cao thì giá trị EMF gây ra càng cao.
Chúng ta có thể viết phương trình trên dưới dạng
$$ E \: \: \ alpha \: \: \ frac {dI} {dt} $$
$$ E \: \: = \: \: L \: \: \ frac {dI} {dt} $$
Ở đâu,
E EMF có được sản xuất không
dI/dt cho biết tốc độ thay đổi của dòng điện
L cho biết suất đồng biến của cuộn cảm.
Tự cảm hoặc Hiệu suất của Tự cảm có thể được gọi là
$$ L \: \: = \: \: \ frac {E} {\ frac {dI} {dt}} $$
Phương trình thực tế được viết dưới dạng
$$ E \: \: = \: \: - L \: \: \ frac {dI} {dt} $$
Số trừ trong phương trình trên chỉ ra rằng the EMF is induced in opposite direction to the voltage source theo định luật Lenz.
Cảm lẫn nhau
Khi cuộn dây mang dòng điện tạo ra một số từ trường xung quanh nó, nếu một cuộn dây khác được đưa đến gần cuộn dây này, sao cho nó nằm trong vùng từ thông của cuộn sơ cấp, thì từ thông thay đổi tạo ra EMF trong cuộn thứ hai. Nếu cuộn dây đầu tiên này được gọi làPrimary coil, cái thứ hai có thể được gọi là Secondary coil.
Khi EMF được cảm ứng trong cuộn thứ cấp do từ trường thay đổi của cuộn sơ cấp, thì hiện tượng đó được gọi là Mutual Inductance.
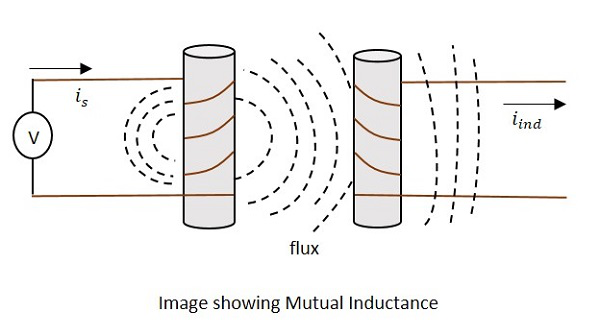
Hiện tại is trong hình chỉ ra nguồn hiện tại trong khi iindcho biết cường độ dòng điện cảm ứng. Từ thông biểu thị từ thông tạo ra xung quanh cuộn dây. Điều này cũng lan truyền đến cuộn dây thứ cấp.
Với ứng dụng của điện áp, dòng điện iscác dòng chảy và thông lượng được tạo ra. Khi hiện tạiis khác nhau, thông lượng được sản xuất khác nhau iind ở cuộn thứ cấp, do tính chất cảm kháng lẫn nhau.
Sự thay đổi đã diễn ra như thế này.
$$ V_ {p} \: \: I_ {p} \ rightarrow \: \: B \: \: \ rightarrow \: \: V_ {s} \: \: I_ {s} $$
Ở đâu,
Vp ip Cho biết Hiệu điện thế và cường độ dòng điện trong cuộn sơ cấp lần lượt là
B Cho biết từ thông
Vs is Cho biết Điện áp và cường độ dòng điện ở cuộn thứ cấp lần lượt là
Cảm lẫn nhau M của hai đầu đoạn mạch mô tả lượng điện áp ở cuộn thứ cấp do dòng điện ở cuộn sơ cấp thay đổi.
$$ V (Phụ) \: \: = \: \: - M \ frac {\ Delta I} {\ Delta t} $$
Trong đó $ \ frac {\ Delta I} {\ Delta t} $ tỷ lệ thay đổi của dòng điện theo thời gian và Mlà đồng hiệu của cảm kháng lẫn nhau. Dấu trừ cho biết chiều dòng điện ngược với nguồn.
Units −
Đơn vị của độ tự cảm tương hỗ là
$$ volt \: \: = \: \: M \ frac {amps} {sec} $$
(Từ phương trình trên)
$$ M \: \: = \: \: \ frac {volt. \: Sec} {amp} $$
$$ = \: \: Henry (H) $$
Tùy thuộc vào số vòng của cuộn sơ cấp và cuộn thứ cấp, liên kết từ thông và lượng EMF cảm ứng khác nhau. Số lượt ở sơ cấp được ký hiệu là N1 và thứ cấp là N2. Hiệu suất đồng ghép nối là thuật ngữ chỉ độ tự cảm lẫn nhau của hai cuộn dây.
Các yếu tố ảnh hưởng đến điện cảm
Có một số yếu tố ảnh hưởng đến hiệu suất của cuộn cảm. Những điều chính được thảo luận dưới đây.
Chiều dài của cuộn dây
Chiều dài của cuộn dây thuần cảm tỉ lệ nghịch với độ tự cảm của cuộn dây. Nếu chiều dài của cuộn dây càng nhiều thì cảm kháng của cuộn cảm đó càng nhỏ và ngược lại.
Diện tích mặt cắt ngang của cuộn dây
Diện tích tiết diện của cuộn dây tỷ lệ thuận với độ tự cảm của cuộn dây. Tiết diện của cuộn dây càng lớn thì độ tự cảm càng tăng.
Số lượt
Với số vòng dây, cuộn dây ảnh hưởng trực tiếp đến độ tự cảm. Giá trị của độ tự cảm bình phương với số vòng dây mà cuộn dây có. Do đó số vòng càng nhiều thì bình phương của nó sẽ là giá trị độ tự cảm của cuộn dây.
Độ thấm của lõi
Các permeability (μ)vật liệu lõi của cuộn cảm chỉ ra sự hỗ trợ mà lõi cung cấp để hình thành từ trường bên trong chính nó. Cáchigher tính thấm của vật liệu lõi, higher sẽ là điện cảm.
Hệ số khớp nối
Đây là một yếu tố quan trọng được biết đến để tính độ tự cảm lẫn nhau của hai cuộn dây. Ta xét hai cuộn dây gần nhau gồm N1 và N2 lần lượt.
Dòng điện qua cuộn thứ nhất i 1 tạo ra từ thông Ψ 1 . Số lượng các liên kết từ thông được hiểu theo các vòng quay.
Gọi cường độ từ thông liên kết với cuộn thứ hai, do dòng điện đơn vị là i 1 là
$$ \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Đây có thể hiểu là Hiệu suất của điện cảm tương hỗ, có nghĩa là
$$ M \: \: = \: \: \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Do đó Hiệu suất của Cảm kháng lẫn nhau giữa hai cuộn dây hoặc đoạn mạch được hiểu là số lần biến thiên trong một cuộn dây do dòng điện trong cuộn dây kia là 1A.
Nếu độ tự cảm của cuộn thứ nhất là L 1 thì
$$ L_ {1} i_ {1} \: \: = \: \: {N_ {1} \ varphi_ {1}} \: \: => \: \: \ frac {L_ {1}} {N_ {1}} \: \: \ frac {\ varphi_ {1}} {i_ {1}} $$
$$ M \: \: = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} $$
Tương tự, hệ số tự cảm do dòng điện i 2 trong cuộn dây thứ hai là
$$ M \: \: = \: \: \ frac {N_ {1} \ varphi_ {2}} {i_ {2}} \: \ dotm \: \ dotm \: \ dotm \: \ dotm \: \ : 1 $$
Nếu độ tự cảm của cuộn thứ hai là L 2
$$ L_ {2} i_ {2} \: \: = \: \: N_ {2} \ varphi_ {2} $$
$$ \ frac {L_ {2}} {N_ {2}} \: \: = \: \: \ frac {\ varphi_ {2}} {i_ {2}} $$
Vì thế,
$$ M \: \: = \: \: \ frac {N_ {1} L_ {2}} {N_ {2}} \: \ dotm \: \ dotm \: \ dotm \: \ dotm \: \: 2 $$
Nhân 1 với 2, ta được
$$ M \: \: \ times \: \: M = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} \: \: \ times \: \: \ frac { N_ {1} L_ {2}} {N_ {2}} $$
$$ M ^ {2} \: \: = \: \: L_ {1} L_ {2} \: \: => \: \: M \: \: = \: \: \ sqrt {L_ {1 } L_ {2}} $$
Phương trình trên đúng khi toàn bộ từ thông thay đổi của cuộn sơ cấp liên kết với cuộn thứ cấp, đây là một trường hợp lý tưởng. Nhưng trong thực tế, nó không phải là trường hợp. Do đó, chúng ta có thể viết là
$$ M \: \: \ neq \: \: \ sqrt {L_ {1} L_ {2}} $$
$$ và \ frac {M} {\ sqrt {L_ {1} L_ {2}}} \: \: = \: \: K \: \: \ neq \: \: 1 $$
Trong đó K được gọi là hệ số ghép nối.
Các Coefficient of coupling K có thể được định nghĩa là tỷ số giữa hệ số tự cảm thực tế và hệ số tự cảm (cực đại) lý tưởng.
Nếu giá trị của k gần với sự thống nhất, thì các cuộn dây được cho là liên kết chặt chẽ và nếu giá trị của k = 0, thì các cuộn dây được cho là được ghép nối lỏng lẻo.
Các ứng dụng của cuộn cảm
Có nhiều ứng dụng của Cuộn cảm, chẳng hạn như -
Cuộn cảm được sử dụng trong các mạch lọc để cảm nhận các thành phần tần số cao và triệt tiêu tín hiệu nhiễu
Để cách ly mạch khỏi các tín hiệu HF không mong muốn.
Cuộn cảm được sử dụng trong các mạch điện để tạo thành một máy biến áp và cách ly các mạch khỏi gai.
Cuộn cảm cũng được sử dụng trong động cơ.