Phân tích dữ liệu lớn - Phương pháp thống kê
Khi phân tích dữ liệu, có thể có một phương pháp thống kê. Các công cụ cơ bản cần thiết để thực hiện phân tích cơ bản là:
- Phân tích tương quan
- Phân tích phương sai
- Kiểm tra giả thuyết
Khi làm việc với các bộ dữ liệu lớn, nó không liên quan đến vấn đề vì các phương pháp này không chuyên sâu về mặt tính toán, ngoại trừ Phân tích tương quan. Trong trường hợp này, luôn có thể lấy mẫu và kết quả phải chắc chắn.
Phân tích tương quan
Phân tích tương quan tìm kiếm mối quan hệ tuyến tính giữa các biến số. Điều này có thể được sử dụng trong các trường hợp khác nhau. Một cách sử dụng phổ biến là phân tích dữ liệu khám phá, trong phần 16.0.2 của cuốn sách có một ví dụ cơ bản về cách tiếp cận này. Trước hết, số liệu tương quan được sử dụng trong ví dụ được đề cập dựa trênPearson coefficient. Tuy nhiên, có một thước đo tương quan thú vị khác không bị ảnh hưởng bởi các yếu tố ngoại lai. Số liệu này được gọi là mối tương quan giữa các mũi nhọn.
Các spearman correlation metric mạnh mẽ hơn đối với sự hiện diện của các giá trị ngoại lệ so với phương pháp Pearson và đưa ra các ước tính tốt hơn về quan hệ tuyến tính giữa biến số khi dữ liệu không được phân phối bình thường.
library(ggplot2)
# Select variables that are interesting to compare pearson and spearman
correlation methods.
x = diamonds[, c('x', 'y', 'z', 'price')]
# From the histograms we can expect differences in the correlations of both
metrics.
# In this case as the variables are clearly not normally distributed, the
spearman correlation
# is a better estimate of the linear relation among numeric variables.
par(mfrow = c(2,2))
colnm = names(x)
for(i in 1:4) {
hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))
}
par(mfrow = c(1,1))Từ biểu đồ trong hình sau, chúng ta có thể mong đợi sự khác biệt trong mối tương quan của cả hai chỉ số. Trong trường hợp này, vì các biến rõ ràng không được phân phối chuẩn, nên tương quan cạnh là một ước lượng tốt hơn về mối quan hệ tuyến tính giữa các biến số.
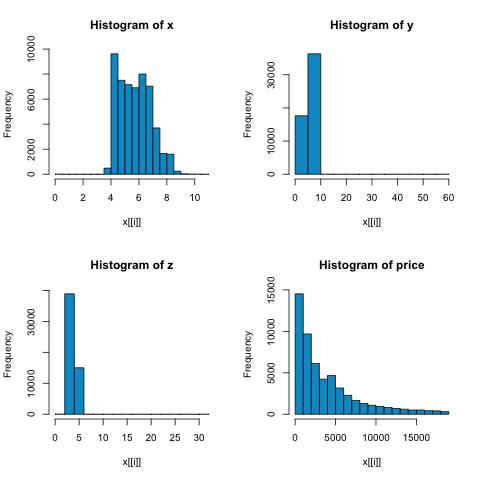
Để tính toán mối tương quan trong R, hãy mở tệp bda/part2/statistical_methods/correlation/correlation.R có phần mã này.
## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson')
cor_spearman <- cor(x, method = 'spearman')
### Pearson Correlation
print(cor_pearson)
# x y z price
# x 1.0000000 0.9747015 0.9707718 0.8844352
# y 0.9747015 1.0000000 0.9520057 0.8654209
# z 0.9707718 0.9520057 1.0000000 0.8612494
# price 0.8844352 0.8654209 0.8612494 1.0000000
### Spearman Correlation
print(cor_spearman)
# x y z price
# x 1.0000000 0.9978949 0.9873553 0.9631961
# y 0.9978949 1.0000000 0.9870675 0.9627188
# z 0.9873553 0.9870675 1.0000000 0.9572323
# price 0.9631961 0.9627188 0.9572323 1.0000000Kiểm tra chi bình phương
Kiểm định chi bình phương cho phép chúng ta kiểm tra xem hai biến ngẫu nhiên có độc lập hay không. Điều này có nghĩa là phân phối xác suất của mỗi biến không ảnh hưởng đến biến khác. Để đánh giá thử nghiệm trong R, trước tiên chúng ta cần tạo một bảng dự phòng, sau đó chuyển bảng chochisq.test R chức năng.
Ví dụ, hãy kiểm tra xem có mối liên hệ giữa các biến: cắt và màu từ tập dữ liệu kim cương hay không. Bài kiểm tra được định nghĩa chính thức là -
- H0: Hình cắt biến đổi và hình thoi là độc lập
- H1: Biến cắt và hình thoi không độc lập
Chúng tôi giả định rằng có mối quan hệ giữa hai biến này theo tên của chúng, nhưng thử nghiệm có thể đưa ra một "quy tắc" khách quan cho biết kết quả này có ý nghĩa như thế nào hay không.
Trong đoạn mã sau, chúng tôi thấy rằng giá trị p của bài kiểm tra là 2,2e-16, điều này gần như bằng không trong điều kiện thực tế. Sau đó, sau khi chạy thử nghiệm,Monte Carlo simulation, chúng tôi nhận thấy rằng giá trị p là 0,0004998, vẫn còn khá thấp hơn ngưỡng 0,05. Kết quả này có nghĩa là chúng tôi bác bỏ giả thuyết vô hiệu (H0), vì vậy chúng tôi tin rằng các biếncut và color không độc lập.
library(ggplot2)
# Use the table function to compute the contingency table
tbl = table(diamonds$cut, diamonds$color)
tbl
# D E F G H I J
# Fair 163 224 312 314 303 175 119
# Good 662 933 909 871 702 522 307
# Very Good 1513 2400 2164 2299 1824 1204 678
# Premium 1603 2337 2331 2924 2360 1428 808
# Ideal 2834 3903 3826 4884 3115 2093 896
# In order to run the test we just use the chisq.test function.
chisq.test(tbl)
# Pearson’s Chi-squared test
# data: tbl
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation
# It's needed to add the simulate.p.value = TRUE flag and the amount of
simulations
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)
# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates)
# data: tbl
# X-squared = 310.32, df = NA, p-value = 0.0004998T-test
Ý tưởng về t-testlà để đánh giá xem có sự khác biệt trong phân phối # biến số giữa các nhóm khác nhau của biến danh nghĩa hay không. Để chứng minh điều này, tôi sẽ chọn các mức của mức Khá và Mức lý tưởng của phần cắt biến nhân tố, sau đó chúng tôi sẽ so sánh các giá trị của một biến số giữa hai nhóm đó.
data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]
data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the
cut variable
df1 = data[, c('cut', 'price')]
# We can see the price means are different for each group
tapply(df1$price, df1$cut, mean)
# Fair Ideal
# 4358.758 3457.542Kiểm tra t được thực hiện trong R với t.testchức năng. Giao diện công thức với t.test là cách đơn giản nhất để sử dụng nó, ý tưởng là một biến số được giải thích bởi một biến nhóm.
Ví dụ: t.test(numeric_variable ~ group_variable, data = data). Trong ví dụ trước,numeric_variable Là price và group_variable Là cut.
Từ góc độ thống kê, chúng tôi đang kiểm tra xem có sự khác biệt trong phân phối của biến số giữa hai nhóm hay không. Về mặt hình thức, kiểm định giả thuyết được mô tả với giả thuyết không (H0) và giả thuyết thay thế (H1).
H0: Không có sự khác biệt trong phân phối biến giá giữa các nhóm Trung bình và Lý tưởng
H1 Có sự khác biệt trong sự phân bổ của biến giá giữa các nhóm Khá và Lý tưởng
Điều sau có thể được thực hiện trong R với mã sau:
t.test(price ~ cut, data = data)
# Welch Two Sample t-test
#
# data: price by cut
# t = 9.7484, df = 1894.8, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# 719.9065 1082.5251
# sample estimates:
# mean in group Fair mean in group Ideal
# 4358.758 3457.542
# Another way to validate the previous results is to just plot the
distributions using a box-plot
plot(price ~ cut, data = data, ylim = c(0,12000),
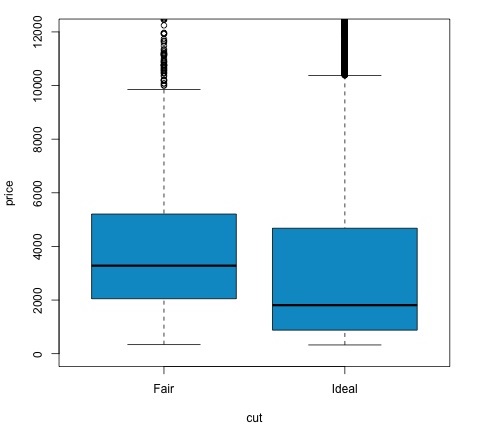
col = 'deepskyblue3')Chúng ta có thể phân tích kết quả thử nghiệm bằng cách kiểm tra nếu giá trị p thấp hơn 0,05. Nếu đúng như vậy, chúng tôi giữ nguyên giả thuyết thay thế. Điều này có nghĩa là chúng tôi đã tìm thấy sự khác biệt về giá giữa hai mức của yếu tố cắt giảm. Theo tên của các cấp độ, chúng tôi đã mong đợi kết quả này, nhưng chúng tôi không thể ngờ rằng giá trung bình trong nhóm Không đạt sẽ cao hơn trong nhóm Lý tưởng. Chúng ta có thể thấy điều này bằng cách so sánh phương tiện của từng yếu tố.
Các plotlệnh tạo ra một đồ thị cho thấy mối quan hệ giữa giá và biến cắt giảm. Đó là một âm mưu hộp; chúng tôi đã đề cập đến biểu đồ này trong phần 16.0.1 nhưng về cơ bản nó cho thấy sự phân phối của biến giá đối với hai mức cắt giảm mà chúng tôi đang phân tích.
Phân tích phương sai
Phân tích phương sai (ANOVA) là một mô hình thống kê dùng để phân tích sự khác biệt giữa các nhóm phân phối bằng cách so sánh giá trị trung bình và phương sai của mỗi nhóm, mô hình được phát triển bởi Ronald Fisher. ANOVA cung cấp một bài kiểm tra thống kê xem liệu phương tiện của một số nhóm có bằng nhau hay không, và do đó tổng quát hóa phép kiểm tra t cho nhiều hơn hai nhóm.
ANOVA hữu ích để so sánh ba hoặc nhiều nhóm về ý nghĩa thống kê vì thực hiện nhiều thử nghiệm t hai mẫu sẽ dẫn đến tăng khả năng mắc lỗi thống kê loại I.
Về mặt cung cấp một giải thích toán học, những điều sau đây là cần thiết để hiểu bài kiểm tra.
x ij = x + (x i - x) + (x ij - x)
Điều này dẫn đến mô hình sau:
x ij = μ + α i + ∈ ij
trong đó μ là trung bình lớn và α i là trung bình nhóm thứ i. Thuật ngữ lỗi ∈ ij được giả định là iid từ phân phối chuẩn. Giả thuyết vô hiệu của bài kiểm tra là -
α 1 = α 2 =… = α k
Về mặt tính toán thống kê thử nghiệm, chúng ta cần tính hai giá trị:
- Tổng bình phương cho giữa hiệu số nhóm -
$$ SSD_B = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {i}}} - \ bar {x}) ^ 2 $$
- Tổng số ô vuông trong nhóm
$$ SSD_W = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {ij}}} - \ bar {x _ {\ bar {i}}}) ^ 2 $$
trong đó SSD B có bậc tự do k − 1 và SSD W có bậc tự do N − k. Sau đó, chúng tôi có thể xác định sự khác biệt bình phương trung bình cho mỗi số liệu.
MS B = SSD B / (k - 1)
MS w = SSD w / (N - k)
Cuối cùng, thống kê kiểm định trong ANOVA được định nghĩa là tỷ số của hai đại lượng trên
F = MS B / MS w
tuân theo phân phối F với k − 1 và N − k bậc tự do. Nếu giả thuyết vô hiệu là đúng, F có thể gần bằng 1. Nếu không, MSB bình phương trung bình giữa nhóm có thể lớn, dẫn đến giá trị F lớn.
Về cơ bản, ANOVA kiểm tra hai nguồn của tổng phương sai và xem phần nào đóng góp nhiều hơn. Đây là lý do tại sao nó được gọi là phân tích phương sai mặc dù mục đích là để so sánh các phương tiện của nhóm.
Về mặt tính toán thống kê, nó thực sự khá đơn giản để thực hiện trong R. Ví dụ sau đây sẽ chứng minh cách nó được thực hiện và vẽ biểu đồ kết quả.
library(ggplot2)
# We will be using the mtcars dataset
head(mtcars)
# mpg cyl disp hp drat wt qsec vs am gear carb
# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
# Let's see if there are differences between the groups of cyl in the mpg variable.
data = mtcars[, c('mpg', 'cyl')]
fit = lm(mpg ~ cyl, data = mtcars)
anova(fit)
# Analysis of Variance Table
# Response: mpg
# Df Sum Sq Mean Sq F value Pr(>F)
# cyl 1 817.71 817.71 79.561 6.113e-10 ***
# Residuals 30 308.33 10.28
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
# Plot the distribution
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')Mã sẽ tạo ra kết quả sau:

Giá trị p mà chúng ta nhận được trong ví dụ này nhỏ hơn đáng kể so với 0,05, vì vậy R trả về ký hiệu '***' để biểu thị điều này. Nó có nghĩa là chúng tôi bác bỏ giả thuyết vô hiệu và chúng tôi tìm thấy sự khác biệt giữa các phương tiện mpg giữa các nhóm khác nhau củacyl Biến đổi.