Phân tích dữ liệu lớn - Phân tích chuỗi thời gian
Chuỗi thời gian là một chuỗi các quan sát của các biến phân loại hoặc số được lập chỉ mục theo ngày hoặc dấu thời gian. Một ví dụ rõ ràng về dữ liệu chuỗi thời gian là chuỗi thời gian của giá cổ phiếu. Trong bảng sau, chúng ta có thể thấy cấu trúc cơ bản của dữ liệu chuỗi thời gian. Trong trường hợp này, các quan sát được ghi lại mỗi giờ.
| Dấu thời gian | Giá cổ phiếu |
|---|---|
| 2015-10-11 09:00:00 | 100 |
| 2015-10-11 10:00:00 | 110 |
| 2015-10-11 11:00:00 | 105 |
| 2015-10-11 12:00:00 | 90 |
| 2015-10-11 13:00:00 | 120 |
Thông thường, bước đầu tiên trong phân tích chuỗi thời gian là vẽ biểu đồ của chuỗi, điều này thường được thực hiện với biểu đồ đường.
Ứng dụng phổ biến nhất của phân tích chuỗi thời gian là dự báo các giá trị trong tương lai của một giá trị số bằng cách sử dụng cấu trúc thời gian của dữ liệu. Điều này có nghĩa là, các quan sát có sẵn được sử dụng để dự đoán các giá trị từ tương lai.
Thứ tự thời gian của dữ liệu, ngụ ý rằng các phương pháp hồi quy truyền thống không hữu ích. Để xây dựng dự báo mạnh mẽ, chúng tôi cần các mô hình có tính đến thứ tự thời gian của dữ liệu.
Mô hình được sử dụng rộng rãi nhất để phân tích chuỗi thời gian được gọi là Autoregressive Moving Average(ARMA). Mô hình bao gồm hai phần, mộtautoregressive (AR) một phần và một moving average(MA) một phần. Sau đó, mô hình này thường được gọi là mô hình ARMA (p, q) trong đó p là bậc của phần tự hồi quy và q là bậc của phần trung bình động.
Mô hình tự phục hồi
Các AR (p) được đọc như một mô hình tự hồi trật tự p. Về mặt toán học, nó được viết là -
$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$
trong đó {φ 1 ,…, φ p } là các tham số được ước lượng, c là hằng số và biến ngẫu nhiên ε t đại diện cho nhiễu trắng. Một số ràng buộc là cần thiết đối với các giá trị của các tham số để mô hình vẫn đứng yên.
Trung bình động
Ký hiệu MA (q) đề cập đến mô hình trung bình động của bậc q -
$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$
trong đó θ 1 , ..., θ q là các tham số của mô hình, μ là kỳ vọng của X t , và ε t , ε t - 1 , ... là các thuật ngữ lỗi nhiễu trắng.
Đường trung bình động tự động hồi phục
Mô hình ARMA (p, q) kết hợp p số hạng tự hồi quy và q số hạng trung bình động. Về mặt toán học, mô hình được biểu diễn theo công thức sau:
$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$
Chúng ta có thể thấy rằng mô hình ARMA (p, q) là sự kết hợp của mô hình AR (p) và MA (q) .
Để cung cấp một số trực giác của mô hình, hãy xem xét rằng phần AR của phương trình tìm cách ước lượng các tham số cho X t - i quan sát để dự đoán giá trị của biến trong X t . Cuối cùng nó là giá trị trung bình có trọng số của các giá trị trong quá khứ. Phần MA sử dụng cách tiếp cận tương tự nhưng với sai số của các quan sát trước đó, ε t - i . Vì vậy, cuối cùng, kết quả của mô hình là một trung bình có trọng số.
Đoạn mã dưới đây trình bày cách thực hiện một ARMA (p, q) trong R .
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)Vẽ sơ đồ dữ liệu thường là bước đầu tiên để tìm hiểu xem có cấu trúc thời gian trong dữ liệu hay không. Chúng ta có thể thấy từ cốt truyện rằng có những đột biến mạnh mẽ vào mỗi cuối năm.
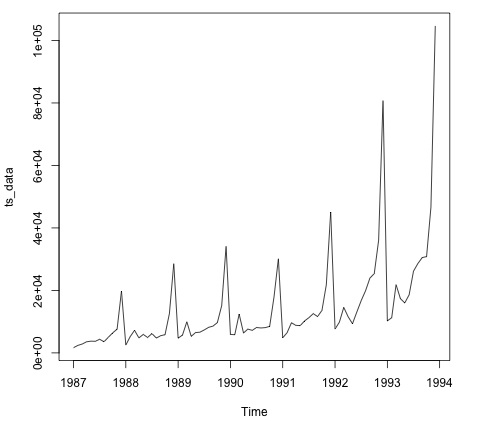
Đoạn mã sau phù hợp với mô hình ARMA với dữ liệu. Nó chạy một số mô hình kết hợp và chọn một mô hình có ít lỗi hơn.
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172