Chuyển đổi 2D
Chuyển đổi có nghĩa là thay đổi một số đồ họa thành một thứ gì đó khác bằng cách áp dụng các quy tắc. Chúng ta có thể có nhiều dạng biến đổi khác nhau như tịnh tiến, tăng giảm tỷ lệ, xoay, cắt,… Khi một phép biến hình diễn ra trên mặt phẳng 2D, nó được gọi là phép biến hình 2D.
Các phép biến đổi đóng một vai trò quan trọng trong đồ họa máy tính để đặt lại vị trí của đồ họa trên màn hình và thay đổi kích thước hoặc hướng của chúng.
Tọa độ đồng nhất
Để thực hiện một chuỗi chuyển đổi, chẳng hạn như dịch theo sau là xoay và chia tỷ lệ, chúng ta cần tuân theo một quy trình tuần tự:
- Dịch các tọa độ,
- Xoay các tọa độ đã dịch, sau đó
- Chia tỷ lệ các tọa độ đã quay để hoàn thành việc chuyển đổi tổng hợp.
Để rút ngắn quá trình này, chúng ta phải sử dụng ma trận biến đổi 3 × 3 thay vì ma trận biến đổi 2 × 2. Để chuyển ma trận 2 × 2 thành ma trận 3 × 3, chúng ta phải thêm một tọa độ giả W.
Bằng cách này, chúng ta có thể biểu diễn điểm bằng 3 số thay vì 2 số, được gọi là Homogenous Coordinatehệ thống. Trong hệ thống này, chúng ta có thể biểu diễn tất cả các phương trình biến đổi trong phép nhân ma trận. Bất kỳ điểm Descartes nào P (X, Y) đều có thể được chuyển đổi thành tọa độ đồng nhất bởi P '(X h , Y h , h).
Dịch
Một phép tịnh tiến di chuyển một đối tượng đến một vị trí khác trên màn hình. Bạn có thể dịch một điểm trong 2D bằng cách thêm tọa độ tịnh tiến (t x , t y ) vào tọa độ gốc (X, Y) để có tọa độ mới (X ', Y').
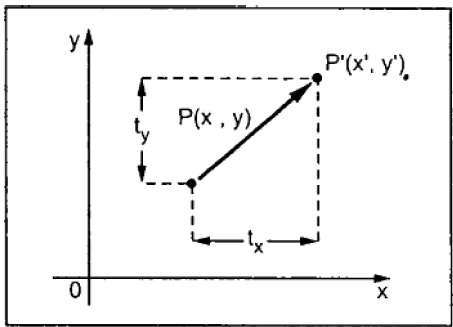
Từ hình trên, bạn có thể viết rằng -
X’ = X + tx
Y’ = Y + ty
Cặp (t x , t y ) được gọi là vectơ tịnh tiến hay vectơ dịch chuyển. Các phương trình trên cũng có thể được biểu diễn bằng cách sử dụng các vectơ cột.
$ P = \ frac {[X]} {[Y]} $ p '= $ \ frac {[X']} {[Y ']} $ T = $ \ frac {[t_ {x}]} {[ t_ {y}]} $
Chúng ta có thể viết nó là -
P’ = P + T
Vòng xoay
Trong phép quay, chúng ta quay đối tượng theo một góc cụ thể θ (theta) so với gốc của nó. Từ hình vẽ sau, ta có thể thấy điểm P (X, Y) nằm ở góc φ so với hoành độ X nằm ngang và cách gốc tọa độ là r.
Giả sử bạn muốn xoay nó theo góc θ. Sau khi xoay nó đến một vị trí mới, bạn sẽ nhận được một điểm mới P '(X', Y ').

Sử dụng lượng giác chuẩn, tọa độ ban đầu của điểm P (X, Y) có thể được biểu diễn dưới dạng:
$ X = r \, cos \, \ phi ...... (1) $
$ Y = r \, sin \, \ phi ...... (2) $
Theo cách tương tự, chúng ta có thể biểu diễn điểm P '(X', Y ') là -
$ {x} '= r \: cos \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: cos \: \ theta \: - \: r \ : sin \: \ phi \: sin \: \ theta ....... (3) $
$ {y} '= r \: sin \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: sin \: \ theta \: + \: r \ : sin \: \ phi \: cos \: \ theta ....... (4) $
Thay phương trình (1) & (2) vào (3) & (4) tương ứng, ta sẽ được
$ {x} '= x \: cos \: \ theta - \: y \: sin \: \ theta $
$ {y} '= x \: sin \: \ theta + \: y \: cos \: \ theta $
Biểu diễn phương trình trên dưới dạng ma trận,
$$ [X 'Y'] = [XY] \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} HOẶC $$
P '= P. R
Trong đó R là ma trận xoay
$$ R = \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} $$
Góc quay có thể dương và âm.
Đối với góc quay dương, chúng ta có thể sử dụng ma trận quay trên. Tuy nhiên, đối với phép quay góc âm, ma trận sẽ thay đổi như hình dưới đây:
$$ R = \ begin {bmatrix} cos (- \ theta) & sin (- \ theta) \\ -sin (- \ theta) & cos (- \ theta) \ end {bmatrix} $$
$$ = \ begin {bmatrix} cos \ theta & −sin \ theta \\ sin \ theta & cos \ theta \ end {bmatrix} \ left (\ bởi vì cos (- \ theta) = cos \ theta \; và \; sin (- \ theta) = −sin \ theta \ right) $$
Mở rộng quy mô
Để thay đổi kích thước của một đối tượng, chuyển đổi tỷ lệ được sử dụng. Trong quá trình chia tỷ lệ, bạn có thể mở rộng hoặc nén các kích thước của đối tượng. Tỷ lệ có thể đạt được bằng cách nhân tọa độ ban đầu của đối tượng với hệ số tỷ lệ để có được kết quả mong muốn.
Giả sử rằng các tọa độ ban đầu là (X, Y), các hệ số tỷ lệ là (S X , S Y ) và các tọa độ được tạo ra là (X ', Y'). Điều này có thể được biểu diễn bằng toán học như hình dưới đây:
X' = X . SX and Y' = Y . SY
Hệ số tỉ lệ S X , S Y tỉ lệ đối tượng tương ứng theo hướng X và Y. Các phương trình trên cũng có thể được biểu diễn dưới dạng ma trận như sau:
$$ \ binom {X '} {Y'} = \ binom {X} {Y} \ begin {bmatrix} S_ {x} & 0 \\ 0 & S_ {y} \ end {bmatrix} $$
HOẶC LÀ
P’ = P . S
Trong đó S là ma trận tỷ lệ. Quá trình chia tỷ lệ được thể hiện trong hình sau.
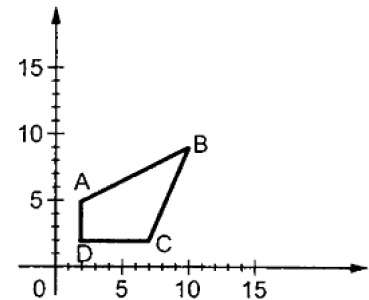
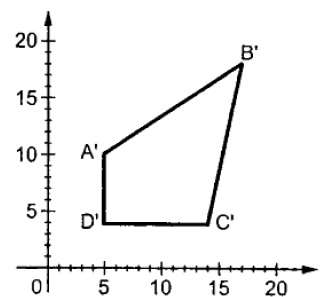
Nếu chúng tôi cung cấp các giá trị nhỏ hơn 1 cho hệ số tỷ lệ S, thì chúng tôi có thể giảm kích thước của đối tượng. Nếu chúng tôi cung cấp các giá trị lớn hơn 1, thì chúng tôi có thể tăng kích thước của đối tượng.
Suy ngẫm
Phản xạ là hình ảnh phản chiếu của vật thể ban đầu. Nói cách khác, chúng ta có thể nói rằng đó là một hoạt động quay với 180 °. Trong phép biến đổi phản xạ, kích thước của vật thể không thay đổi.
Các hình sau cho thấy phản xạ đối với trục X và Y, và về điểm gốc tương ứng.
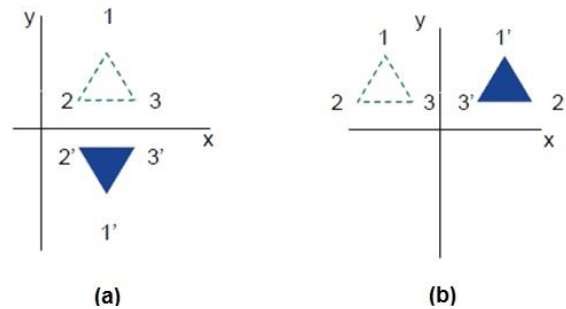
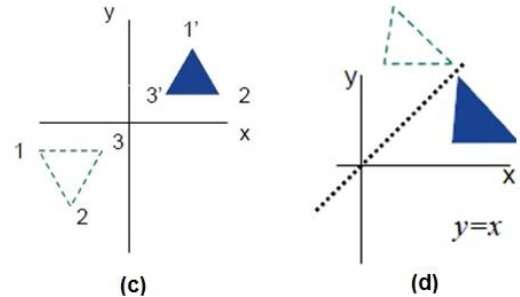
Shear
Một phép biến hình làm nghiêng hình dạng của một vật thể được gọi là phép biến hình cắt. Có hai phép biến đổi cắtX-Shear và Y-Shear. Một thay đổi các giá trị tọa độ X và các giá trị tọa độ Y thay đổi khác. Tuy nhiên; trong cả hai trường hợp, chỉ một tọa độ thay đổi tọa độ của nó và tọa độ khác giữ nguyên giá trị của nó. Cắt xén còn được gọi làSkewing.
X-Shear
X-Shear bảo toàn tọa độ Y và các thay đổi được thực hiện đối với tọa độ X, điều này làm cho các đường thẳng đứng nghiêng sang phải hoặc sang trái như thể hiện trong hình dưới đây.
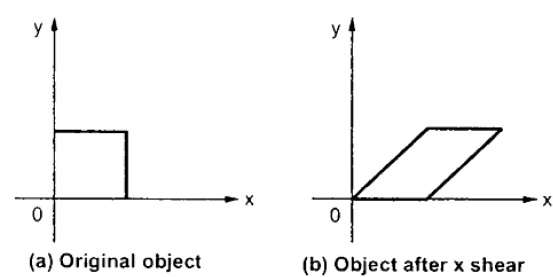
Ma trận biến đổi cho X-Shear có thể được biểu diễn dưới dạng:
$$ X_ {sh} = \ begin {bmatrix} 1 & shx & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Y '= Y + Sh y . X
X '= X
Y-Shear
Y-Shear bảo toàn tọa độ X và thay đổi tọa độ Y làm cho các đường nằm ngang biến đổi thành các đường dốc lên hoặc xuống như thể hiện trong hình sau.
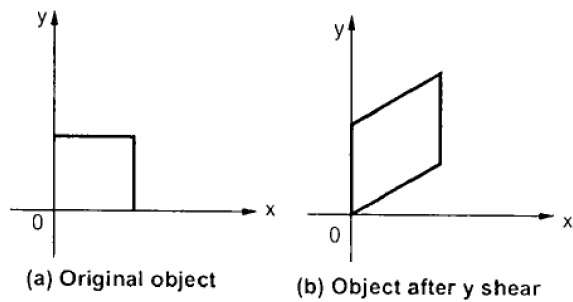
Y-Shear có thể được biểu diễn trong ma trận từ:
$$ Y_ {sh} \ begin {bmatrix} 1 & 0 & 0 \\ nhút nhát & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
X '= X + Sh x . Y
Y '= Y
Chuyển đổi tổng hợp
Nếu một phép biến đổi của mặt phẳng T1 được theo sau bởi phép biến đổi mặt phẳng thứ hai T2, thì bản thân kết quả có thể được biểu diễn bằng một phép biến đổi duy nhất T là thành phần của T1 và T2 được lấy theo thứ tự đó. Điều này được viết là T = T1 ∙ T2.
Phép biến đổi tổng hợp có thể đạt được bằng cách ghép các ma trận biến đổi để thu được ma trận biến đổi kết hợp.
Một ma trận kết hợp -
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
Trong đó [Ti] là bất kỳ sự kết hợp nào của
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
Sự thay đổi thứ tự của phép biến đổi sẽ dẫn đến các kết quả khác nhau, vì nói chung phép nhân ma trận không có tính tích lũy, đó là [A]. [B] ≠ [B]. [A] và thứ tự của phép nhân. Mục đích cơ bản của việc soạn thảo các phép biến đổi là để đạt được hiệu quả bằng cách áp dụng một phép biến đổi có cấu trúc đơn lẻ cho một điểm, thay vì áp dụng một loạt phép biến đổi lần lượt.
Ví dụ, để xoay một đối tượng về một điểm tùy ý (X p , Y p ), chúng ta phải thực hiện ba bước:
- Dịch điểm (X p , Y p ) về gốc tọa độ.
- Xoay nó về nguồn gốc.
- Cuối cùng, dịch tâm quay trở lại nơi nó thuộc về.