Chuyển đổi 3D

Vòng xoay

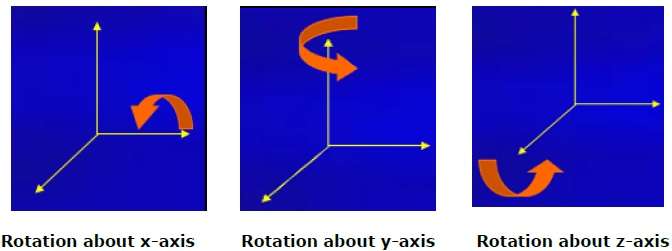
Xoay 3D không giống như xoay 2D. Trong phép quay 3D, chúng ta phải xác định góc quay cùng với trục quay. Chúng ta có thể thực hiện xoay 3D về các trục X, Y và Z. Chúng được biểu diễn dưới dạng ma trận như sau:

$$ R_ {x} (\ theta) = \ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos \ theta & −sin \ theta & 0 \\ 0 & sin \ theta & cos \ theta & 0 \\ 0 & 0 & 0 & 1 \ \ \ end {bmatrix} R_ {y} (\ theta) = \ begin {bmatrix} cos \ theta & 0 & sin \ theta & 0 \\ 0 & 1 & 0 & 0 \\ −sin \ theta & 0 & cos \ theta & 0 \\ 0 & 0 & 0 & 1 \\ \ end {bmatrix} R_ {z} (\ theta) = \ begin {bmatrix} cos \ theta & −sin \ theta & 0 & 0 \\ sin \ theta & cos \ theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $$

Hình sau giải thích chuyển động quay về các trục khác nhau:

Mở rộng quy mô

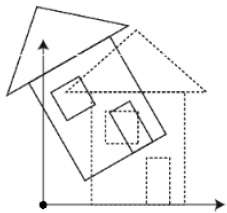
Bạn có thể thay đổi kích thước của một đối tượng bằng cách sử dụng chuyển đổi tỷ lệ. Trong quá trình chia tỷ lệ, bạn có thể mở rộng hoặc nén các kích thước của đối tượng. Tỷ lệ có thể đạt được bằng cách nhân tọa độ ban đầu của đối tượng với hệ số tỷ lệ để có được kết quả mong muốn. Hình sau đây cho thấy hiệu quả của việc chia tỷ lệ 3D:

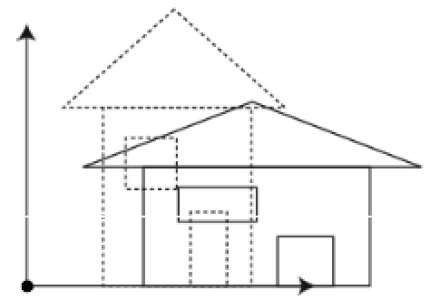
Trong hoạt động chia tỷ lệ 3D, ba tọa độ được sử dụng. Giả sử rằng tọa độ ban đầu là (X, Y, Z), hệ số tỷ lệ lần lượt là $ (S_ {X,} S_ {Y,} S_ {z}) $ và tọa độ được tạo ra là (X ', Y' , Z '). Điều này có thể được biểu diễn bằng toán học như hình dưới đây:

$ S = \ begin {bmatrix} S_ {x} & 0 & 0 & 0 \\ 0 & S_ {y} & 0 & 0 \\ 0 & 0 & S_ {z} & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $

P '= P ∙ S

$ [{X} '\: \: \: {Y}' \: \: \: {Z} '\: \: \: 1] = [X \: \: \: Y \: \: \: Z \: \: \: 1] \: \: \ begin {bmatrix} S_ {x} & 0 & 0 & 0 \\ 0 & S_ {y} & 0 & 0 \\ 0 & 0 & S_ {z} & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $

$ = [X.S_ {x} \: \: \: Y.S_ {y} \: \: \: Z.S_ {z} \: \: \: 1] $

Shear

Một phép biến đổi làm nghiêng hình dạng của một đối tượng được gọi là shear transformation. Giống như cắt 2D, chúng ta có thể cắt một vật thể dọc theo trục X, trục Y hoặc trục Z trong 3D.

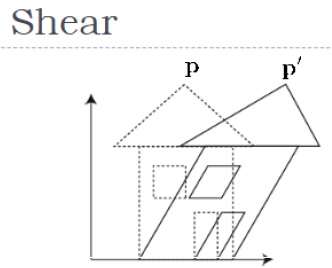
Như trong hình trên, có một tọa độ P. Bạn có thể cắt nó để có một tọa độ mới P ', có thể được biểu diễn dưới dạng ma trận 3D như dưới đây:

$ Sh = \ begin {bmatrix} 1 & sh_ {x} ^ {y} & sh_ {x} ^ {z} & 0 \\ sh_ {y} ^ {x} & 1 & sh_ {y} ^ {z} & 0 \\ sh_ {z} ^ {x} & sh_ {z} ^ {y} & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $

P '= P ∙ Sh

$ X '= X + Sh_ {x} ^ {y} Y + Sh_ {x} ^ {z} Z $

$ Y '= Sh_ {y} ^ {x} X + Y + sh_ {y} ^ {z} Z $

$ Z '= Sh_ {z} ^ {x} X + Sh_ {z} ^ {y} Y + Z $

Ma trận chuyển đổi

Ma trận chuyển đổi là một công cụ cơ bản để biến đổi. Một ma trận với kích thước nxm được nhân với tọa độ của các đối tượng. Thường sử dụng ma trận 3 x 3 hoặc 4 x 4 để biến đổi. Ví dụ, hãy xem xét ma trận sau đây cho các hoạt động khác nhau.

$ T = \ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ t_ {x} & t_ {y} & t_ {z} & 1 \\ \ end {bmatrix} $	$ S = \ begin {bmatrix} S_ {x} & 0 & 0 & 0 \\ 0 & S_ {y} & 0 & 0 \\ 0 & 0 & S_ {z} & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $	$ Sh = \ begin {bmatrix} 1 & sh_ {x} ^ {y} & sh_ {x} ^ {z} & 0 \\ sh_ {y} ^ {x} & 1 & sh_ {y} ^ {z} & 0 \\ sh_ {z} ^ {x} & sh_ {z} ^ {y} & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $
Translation Matrix	Scaling Matrix	Shear Matrix
$ R_ {x} (\ theta) = \ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos \ theta & -sin \ theta & 0 \\ 0 & sin \ theta & cos \ theta & 0 \\ 0 & 0 & 0 & 1 \\ \ end {bmatrix} $	$ R_ {y} (\ theta) = \ begin {bmatrix} cos \ theta & 0 & sin \ theta & 0 \\ 0 & 1 & 0 & 0 \\ -sin \ theta & 0 & cos \ theta & 0 \\ 0 & 0 & 0 & 1 \\ \ end {bmatrix} $	$ R_ {z} (\ theta) = \ begin {bmatrix} cos \ theta & -sin \ theta & 0 & 0 \\ sin \ theta & cos \ theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $
Rotation Matrix