Đường cong đồ họa máy tính

Trong đồ họa máy tính, chúng ta thường cần vẽ các loại đối tượng khác nhau lên màn hình. Các đối tượng không phải lúc nào cũng phẳng và chúng ta cần phải vẽ các đường cong nhiều lần để vẽ một đối tượng.

Các loại đường cong

Đường cong là một tập hợp các điểm lớn vô hạn. Mỗi điểm có hai lân cận ngoại trừ các điểm cuối. Các đường cong có thể được phân loại rộng rãi thành ba loại:explicit, implicit, và parametric curves.

Đường cong ngầm

Biểu diễn đường cong ngầm định xác định tập hợp các điểm trên một đường cong bằng cách sử dụng một thủ tục có thể kiểm tra xem có một điểm nằm trên đường cong hay không. Thông thường, một đường cong ngầm định được xác định bởi một hàm ngầm định của dạng -

f (x, y) = 0

Nó có thể đại diện cho các đường cong đa giá trị (nhiều giá trị y cho một giá trị x). Một ví dụ phổ biến là vòng tròn, có đại diện ngầm định là

x² + y² - R² = 0

Đường cong rõ ràng

Một hàm toán học y = f (x) có thể được vẽ dưới dạng một đường cong. Một hàm như vậy là biểu diễn rõ ràng của đường cong. Biểu diễn rõ ràng không chung chung, vì nó không thể biểu diễn các đường thẳng đứng và cũng có giá trị đơn. Đối với mỗi giá trị của x, chỉ có một giá trị duy nhất của y được hàm thường tính.

Đường cong tham số

Các đường cong có dạng tham số được gọi là đường cong tham số. Các biểu diễn đường cong rõ ràng và ngầm định chỉ có thể được sử dụng khi đã biết hàm. Trong thực tế, các đường cong tham số được sử dụng. Đường cong tham số hai chiều có dạng sau:

P (t) = f (t), g (t) hoặc P (t) = x (t), y (t)

Các hàm f và g trở thành tọa độ (x, y) của bất kỳ điểm nào trên đường cong, và các điểm thu được khi tham số t thay đổi trong một khoảng [a, b] nào đó, bình thường là [0, 1].

Đường cong Bezier

Đường cong Bezier được phát hiện bởi kỹ sư người Pháp Pierre Bézier. Các đường cong này có thể được tạo ra dưới sự kiểm soát của các điểm khác. Các tiếp tuyến gần đúng bằng cách sử dụng các điểm kiểm soát được sử dụng để tạo đường cong. Đường cong Bezier có thể được biểu diễn bằng toán học như sau:

$$ \ sum_ {k = 0} ^ {n} P_ {i} {B_ {i} ^ {n}} (t) $$

Trong đó $ p_ {i} $ là tập hợp các điểm và $ {B_ {i} ^ {n}} (t) $ đại diện cho các đa thức Bernstein được cho bởi -

$$ {B_ {i} ^ {n}} (t) = \ binom {n} {i} (1 - t) ^ {ni} t ^ {i} $$

Ở đâu n là bậc đa thức, i là chỉ số, và t là biến.

Đường cong Bézier đơn giản nhất là đường thẳng từ điểm $ P_ {0} $ đến $ P_ {1} $. Đường cong Bezier bậc hai được xác định bởi ba điểm kiểm soát. Một đường cong Bezier khối được xác định bởi bốn điểm kiểm soát.

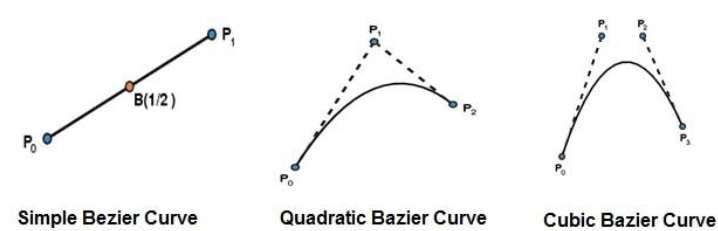
Tính chất của đường cong Bezier

Đường cong Bezier có các đặc tính sau:

Chúng thường tuân theo hình dạng của đa giác điều khiển, bao gồm các đoạn nối các điểm điều khiển.
Chúng luôn đi qua điểm kiểm soát đầu tiên và cuối cùng.
Chúng được chứa trong vỏ lồi của các điểm kiểm soát xác định của chúng.
Bậc của đa thức xác định đoạn đường cong nhỏ hơn một bậc của đa thức xác định điểm. Do đó, đối với 4 điểm điều khiển, bậc của đa thức là 3, tức là đa thức bậc ba.
Đường cong Bezier thường tuân theo hình dạng của đa giác xác định.
Hướng của vectơ tiếp tuyến tại các điểm cuối giống với hướng của vectơ được xác định bởi đoạn đầu và đoạn cuối.
Thuộc tính lồi của đường cong Bezier đảm bảo rằng đa thức tuân theo các điểm điều khiển một cách trơn tru.
Không có đường thẳng nào cắt đường cong Bezier nhiều lần hơn đường thẳng cắt đa giác điều khiển của nó.
Chúng bất biến dưới một phép biến đổi affine.
Đường cong Bezier thể hiện khả năng kiểm soát toàn cục có nghĩa là di chuyển một điểm kiểm soát sẽ làm thay đổi hình dạng của toàn bộ đường cong.
Một đường cong Bezier đã cho có thể được chia nhỏ tại điểm t = t0 thành hai đoạn Bezier nối với nhau tại điểm tương ứng với giá trị tham số t = t0.

Đường cong B-Spline

Đường cong Bezier được tạo ra bởi hàm cơ sở Bernstein có tính linh hoạt hạn chế.

Đầu tiên, số lượng đỉnh đa giác được chỉ định sẽ sửa thứ tự của đa thức kết quả xác định đường cong.
Đặc điểm giới hạn thứ hai là giá trị của hàm pha trộn là khác không đối với tất cả các giá trị tham số trên toàn bộ đường cong.

Cơ sở B-spline chứa cơ sở Bernstein là trường hợp đặc biệt. Cơ sở B-spline là phi toàn cầu.

Đường cong B-spline được định nghĩa là sự kết hợp tuyến tính của các điểm điều khiển Pi và hàm cơ sở B-spline $ N_ {i,} $ k (t) cho bởi

$ C (t) = \ sum_ {i = 0} ^ {n} P_ {i} N_ {i, k} (t), $ $ n \ geq k-1, $ $ t \: \ epsilon \: [ tk-1, tn + 1] $

Ở đâu,

{$ p_ {i} $: i = 0, 1, 2… .n} là các điểm kiểm soát
k là bậc của các đoạn đa thức của đường cong B-spline. Thứ tự k có nghĩa là đường cong được tạo thành từ các đoạn đa thức từng mảnh có bậc k - 1,
$ N_ {i, k} (t) $ là “hàm trộn B-spline chuẩn hóa”. Chúng được mô tả bởi bậc k và bởi một dãy số thực không giảm thường được gọi là "dãy nút".

$$ {t_ {i}: i = 0, ... n + K} $$

N _i , k hàm được mô tả như sau:

$$ N_ {i, 1} (t) = \ left \ {\ begin {matrix} 1, & if \: u \: \ epsilon \: [t_ {i,} t_ {i + 1}) \\ 0 & Nếu không thì \ end {matrix} \ right. $$

và nếu k> 1,

$$ N_ {i, k} (t) = \ frac {t-t_ {i}} {t_ {i + k-1}} N_ {i, k-1} (t) + \ frac {t_ {i + k} -t} {t_ {i + k} - t_ {i + 1}} N_ {i + 1, k-1} (t) $$

và

$$ t \: \ epsilon \: [t_ {k-1}, t_ {n + 1}) $$

Thuộc tính của đường cong B-spline

Đường cong B-spline có các đặc tính sau:

Tổng của các hàm cơ sở B-spline cho bất kỳ giá trị tham số nào là 1.
Mỗi hàm cơ sở là số dương hoặc bằng không đối với tất cả các giá trị tham số.
Mỗi hàm cơ sở có đúng một giá trị lớn nhất, ngoại trừ k = 1.
Bậc lớn nhất của đường cong bằng số đỉnh của đa giác xác định.
Bậc của đa thức B-spline không phụ thuộc vào số đỉnh của đa giác xác định.
B-spline cho phép điều khiển cục bộ trên bề mặt đường cong vì mỗi đỉnh chỉ ảnh hưởng đến hình dạng của đường cong trên một phạm vi giá trị tham số trong đó hàm cơ sở liên quan của nó là số khác.
Đường cong thể hiện tính chất giảm dần biến thiên.
Đường cong thường tuân theo hình dạng của đa giác xác định.
Bất kỳ phép biến đổi affine nào cũng có thể được áp dụng cho đường cong bằng cách áp dụng nó cho các đỉnh của đa giác xác định.
Đường cong bên trong vỏ lồi của đa giác xác định của nó.