Đồ họa máy tính Fractals

Một nhà toán học Pháp / Mỹ, Tiến sĩ Benoit Mandelbrot đã phát hiện ra Fractals. Từ fractal có nguồn gốc từ một từ fractus trong tiếng Latinh có nghĩa là gãy.

Fractals là gì?

Fractals là những hình ảnh rất phức tạp do máy tính tạo ra từ một công thức duy nhất. Chúng được tạo bằng cách sử dụng lặp lại. Điều này có nghĩa là một công thức được lặp đi lặp lại với các giá trị hơi khác nhau, có tính đến kết quả từ lần lặp trước.

Fractal được sử dụng trong nhiều lĩnh vực như -

Astronomy - Để phân tích các thiên hà, các vành đai của Sao Thổ, v.v.
Biology/Chemistry - Để mô tả nền văn hóa vi khuẩn, phản ứng hóa học, giải phẫu người, phân tử, thực vật,
Others - Để miêu tả các đám mây, đường bờ biển và đường biên giới, nén dữ liệu, khuếch tán, kinh tế, nghệ thuật fractal, nhạc fractal, phong cảnh, hiệu ứng đặc biệt, v.v.

Thế hệ Fractals

Fractal có thể được tạo ra bằng cách lặp đi lặp lại cùng một hình dạng như trong hình sau. Trong hình (a) cho thấy một tam giác đều. Trong hình (b), chúng ta có thể thấy rằng tam giác được lặp lại để tạo ra một hình giống như ngôi sao. Trong hình (c), chúng ta có thể thấy rằng hình ngôi sao trong hình (b) được lặp đi lặp lại nhiều lần để tạo ra một hình mới.

Chúng ta có thể lặp lại số lần không giới hạn để tạo ra một hình dạng mong muốn. Trong thuật ngữ lập trình, đệ quy được sử dụng để tạo ra các hình dạng như vậy.

Fractal hình học

Fractal hình học xử lý các hình dạng được tìm thấy trong tự nhiên có kích thước không phải là số nguyên hoặc kiểu fractal. Để xây dựng một Fractal tự xác định (phirandom) về mặt hình học, chúng ta bắt đầu với một hình dạng hình học nhất định, được gọi làinitiator. Các phần con của trình khởi tạo sau đó được thay thế bằng một mẫu, được gọi làgenerator.

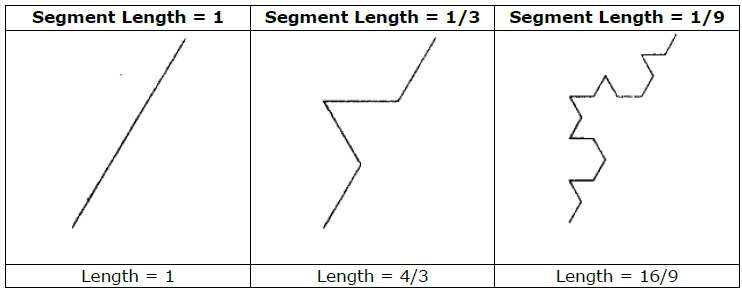
Ví dụ, nếu chúng ta sử dụng bộ khởi tạo và bộ tạo được hiển thị trong hình trên, chúng ta có thể tạo ra một mẫu tốt bằng cách lặp lại nó. Mỗi đoạn thẳng trong trình khởi tạo được thay thế bằng bốn đoạn thẳng có độ dài bằng nhau ở mỗi bước. Hệ số tỷ lệ là 1/3, do đó kích thước Fractal là D = ln 4 / ln 3 ≈ 1.2619.

Ngoài ra, độ dài của mỗi đoạn thẳng trong bộ khởi tạo tăng thêm hệ số 4/3 ở mỗi bước, do đó độ dài của đường cong gãy khúc có xu hướng vô cùng khi nhiều chi tiết hơn được thêm vào đường cong như thể hiện trong hình sau: