DAA - Binary Heap

Có một số loại heap, tuy nhiên trong chương này, chúng ta sẽ thảo luận về heap nhị phân. Abinary heaplà một cấu trúc dữ liệu, trông tương tự như một cây nhị phân hoàn chỉnh. Cấu trúc dữ liệu đống tuân theo các thuộc tính sắp xếp được thảo luận dưới đây. Nói chung, một Heap được biểu diễn bằng một mảng. Trong chương này, chúng tôi đại diện cho một đốngH.

Khi các phần tử của một đống được lưu trữ trong một mảng, coi chỉ số bắt đầu là 1, vị trí của nút cha của i^th phần tử có thể được tìm thấy tại ⌊ i/2 ⌋. Con trái và con phải củai^th nút ở vị trí 2i và 2i + 1.

Một đống nhị phân có thể được phân loại thêm là max-heap hoặc một min-heap dựa trên thuộc tính đặt hàng.

Max-Heap

Trong heap này, giá trị khóa của một nút lớn hơn hoặc bằng giá trị khóa của nút con cao nhất.

Vì thế, H[Parent(i)] ≥ H[i]

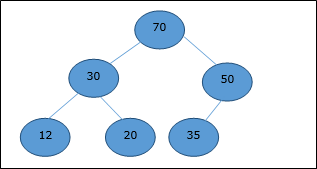
Min-Heap

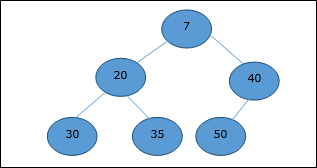
Trong trung bình, giá trị khóa của một nút nhỏ hơn hoặc bằng giá trị khóa của nút con thấp nhất.

Vì thế, H[Parent(i)] ≤ H[i]

Trong bối cảnh này, các hoạt động cơ bản được hiển thị bên dưới đối với Max-Heap. Việc chèn và xóa các phần tử trong và từ đống cần sắp xếp lại các phần tử. Vì thế,Heapify chức năng cần được gọi.

Biểu diễn mảng

Một cây nhị phân hoàn chỉnh có thể được biểu diễn bằng một mảng, lưu trữ các phần tử của nó bằng cách sử dụng truyền qua thứ tự mức.

Chúng ta hãy xem xét một đống (như được hiển thị bên dưới) sẽ được đại diện bởi một mảng H.

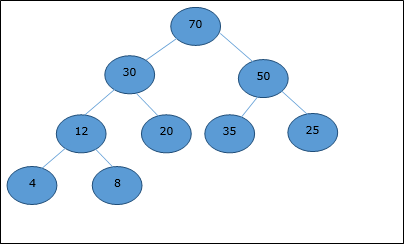
Xem xét chỉ số bắt đầu là 0, sử dụng truyền qua thứ tự cấp, các phần tử đang được giữ trong một mảng như sau.

Index	0	1	2	3	4	5	6	7	số 8	...
elements	70	30	50	12	20	35	25	4	số 8	...

Trong bối cảnh này, các hoạt động trên heap đang được biểu diễn đối với Max-Heap.

Để tìm chỉ mục của phần tử gốc của một phần tử tại chỉ mục i, thuật toán sau Parent (numbers[], i) Được sử dụng.

Algorithm: Parent (numbers[], i) 
if i == 1 
   return NULL 
else 
   [i / 2]

Chỉ mục của phần tử con bên trái của một phần tử tại chỉ mục i có thể được tìm thấy bằng cách sử dụng thuật toán sau, Left-Child (numbers[], i).

Algorithm: Left-Child (numbers[], i) 
If 2 * i ≤ heapsize 
   return [2 * i] 
else 
   return NULL

Chỉ mục của con bên phải của một phần tử tại chỉ mục i có thể được tìm thấy bằng cách sử dụng thuật toán sau, Right-Child(numbers[], i).

Algorithm: Right-Child (numbers[], i) 
if 2 * i < heapsize 
   return [2 * i + 1] 
else 
   return NULL