DAA - Hướng dẫn nhanh
Thuật toán là một tập hợp các bước hoạt động để giải quyết một vấn đề thực hiện các tác vụ tính toán, xử lý dữ liệu và lập luận tự động. Thuật toán là một phương pháp hiệu quả có thể được thể hiện trong khoảng thời gian và không gian hữu hạn.
Thuật toán là cách tốt nhất để biểu diễn giải pháp của một vấn đề cụ thể một cách rất đơn giản và hiệu quả. Nếu chúng ta có một thuật toán cho một vấn đề cụ thể, thì chúng ta có thể triển khai nó bằng bất kỳ ngôn ngữ lập trình nào, nghĩa làalgorithm is independent from any programming languages.
Thiết kế thuật toán
Các khía cạnh quan trọng của thiết kế thuật toán bao gồm tạo ra một thuật toán hiệu quả để giải quyết vấn đề một cách hiệu quả bằng cách sử dụng thời gian và không gian tối thiểu.
Để giải quyết một vấn đề, có thể tuân theo các cách tiếp cận khác nhau. Một số trong số chúng có thể hiệu quả về mức tiêu thụ thời gian, trong khi các phương pháp khác có thể hiệu quả về bộ nhớ. Tuy nhiên, một điều cần lưu ý là không thể đồng thời tối ưu hóa cả tiêu thụ thời gian và sử dụng bộ nhớ. Nếu chúng ta yêu cầu một thuật toán chạy trong thời gian ngắn hơn, chúng ta phải đầu tư vào nhiều bộ nhớ hơn và nếu chúng ta yêu cầu một thuật toán chạy với bộ nhớ ít hơn, chúng ta cần có nhiều thời gian hơn.
Các bước phát triển vấn đề
Các bước sau đây liên quan đến việc giải quyết các vấn đề tính toán.
- Định nghĩa vấn đề
- Phát triển một mô hình
- Đặc điểm kỹ thuật của một thuật toán
- Thiết kế một thuật toán
- Kiểm tra tính đúng đắn của một thuật toán
- Phân tích một thuật toán
- Triển khai một thuật toán
- Thử nghiệm chương trình
- Documentation
Đặc điểm của thuật toán
Các đặc điểm chính của thuật toán như sau:
Các thuật toán phải có một tên duy nhất
Các thuật toán phải có tập hợp đầu vào và đầu ra được xác định rõ ràng
Các thuật toán được sắp xếp hợp lý với các hoạt động rõ ràng
Các thuật toán tạm dừng trong một khoảng thời gian hữu hạn. Các thuật toán không nên chạy đến vô cùng, tức là, một thuật toán phải kết thúc tại một số điểm
Mã giả
Mã giả đưa ra mô tả cấp cao của một thuật toán mà không có sự mơ hồ liên quan đến văn bản thuần túy nhưng cũng không cần biết cú pháp của một ngôn ngữ lập trình cụ thể.
Thời gian chạy có thể được ước tính theo cách tổng quát hơn bằng cách sử dụng Mã giả để biểu diễn thuật toán như một tập hợp các hoạt động cơ bản sau đó có thể được tính.
Sự khác biệt giữa Thuật toán và Mã giả
Thuật toán là một định nghĩa chính thức với một số đặc điểm cụ thể mô tả một quá trình, có thể được thực thi bởi một máy tính hoàn chỉnh Turing để thực hiện một tác vụ cụ thể. Nói chung, từ "thuật toán" có thể được sử dụng để mô tả bất kỳ nhiệm vụ cấp cao nào trong khoa học máy tính.
Mặt khác, mã giả là một mô tả không chính thức và (thường là thô sơ) con người có thể đọc được về một thuật toán để lại nhiều chi tiết cụ thể về nó. Viết mã giả không có giới hạn về kiểu dáng và mục tiêu duy nhất của nó là mô tả các bước cấp cao của thuật toán theo cách thực tế nhiều bằng ngôn ngữ tự nhiên.
Ví dụ, sau đây là một thuật toán cho Sắp xếp Chèn.
Algorithm: Insertion-Sort
Input: A list L of integers of length n
Output: A sorted list L1 containing those integers present in L
Step 1: Keep a sorted list L1 which starts off empty
Step 2: Perform Step 3 for each element in the original list L
Step 3: Insert it into the correct position in the sorted list L1.
Step 4: Return the sorted list
Step 5: StopĐây là một mã giả mô tả quá trình trừu tượng cấp cao được đề cập ở trên trong thuật toán Chèn-Sắp xếp có thể được mô tả theo cách thực tế hơn.
for i <- 1 to length(A)
x <- A[i]
j <- i
while j > 0 and A[j-1] > x
A[j] <- A[j-1]
j <- j - 1
A[j] <- xTrong hướng dẫn này, các thuật toán sẽ được trình bày dưới dạng mã giả, tương tự về nhiều khía cạnh với C, C ++, Java, Python và các ngôn ngữ lập trình khác.
Trong phân tích lý thuyết các thuật toán, người ta thường ước lượng độ phức tạp của chúng theo nghĩa tiệm cận, tức là ước tính hàm phức tạp cho đầu vào lớn tùy ý. Thời hạn"analysis of algorithms" được đặt ra bởi Donald Knuth.
Phân tích thuật toán là một phần quan trọng của lý thuyết độ phức tạp tính toán, lý thuyết này cung cấp ước tính lý thuyết cho các tài nguyên cần thiết của một thuật toán để giải quyết một vấn đề tính toán cụ thể. Hầu hết các thuật toán được thiết kế để làm việc với các đầu vào có độ dài tùy ý. Phân tích các thuật toán là việc xác định lượng tài nguyên thời gian và không gian cần thiết để thực thi nó.
Thông thường, hiệu quả hoặc thời gian chạy của một thuật toán được nêu dưới dạng một hàm liên quan đến độ dài đầu vào với số bước, được gọi là time complexity, hoặc khối lượng bộ nhớ, được gọi là space complexity.
Nhu cầu phân tích
Trong chương này, chúng ta sẽ thảo luận về nhu cầu phân tích các thuật toán và cách chọn một thuật toán tốt hơn cho một bài toán cụ thể vì một bài toán tính toán có thể được giải bằng các thuật toán khác nhau.
Bằng cách xem xét một thuật toán cho một vấn đề cụ thể, chúng ta có thể bắt đầu phát triển nhận dạng mẫu để các loại vấn đề tương tự có thể được giải quyết nhờ sự trợ giúp của thuật toán này.
Các thuật toán thường khá khác biệt với nhau, mặc dù mục tiêu của các thuật toán này là giống nhau. Ví dụ, chúng ta biết rằng một tập hợp các số có thể được sắp xếp bằng các thuật toán khác nhau. Số lượng phép so sánh được thực hiện bởi một thuật toán có thể thay đổi với các thuật toán khác cho cùng một đầu vào. Do đó, độ phức tạp về thời gian của các thuật toán đó có thể khác nhau. Đồng thời, chúng ta cần tính toán không gian bộ nhớ theo yêu cầu của từng thuật toán.
Phân tích thuật toán là quá trình phân tích khả năng giải quyết vấn đề của thuật toán về thời gian và kích thước cần thiết (dung lượng bộ nhớ để lưu trữ trong khi thực hiện). Tuy nhiên, mối quan tâm chính của việc phân tích các thuật toán là thời gian hoặc hiệu suất cần thiết. Nói chung, chúng tôi thực hiện các loại phân tích sau:
Worst-case - Số bước tối đa được thực hiện trên mọi trường hợp có kích thước a.
Best-case - Số bước tối thiểu được thực hiện trên bất kỳ trường hợp nào có kích thước a.
Average case - Số bước trung bình được thực hiện trên bất kỳ trường hợp nào có kích thước a.
Amortized - Một chuỗi các hoạt động được áp dụng cho đầu vào của kích thước a tính trung bình theo thời gian.
Để giải quyết một vấn đề, chúng ta cần xem xét độ phức tạp về thời gian cũng như không gian vì chương trình có thể chạy trên một hệ thống mà bộ nhớ bị hạn chế nhưng vẫn có đủ dung lượng hoặc có thể ngược lại. Trong bối cảnh này, nếu chúng ta so sánhbubble sort và merge sort. Sắp xếp bong bóng không yêu cầu bộ nhớ bổ sung, nhưng sắp xếp hợp nhất yêu cầu thêm không gian. Mặc dù độ phức tạp về thời gian của sắp xếp bong bóng cao hơn so với sắp xếp hợp nhất, chúng tôi có thể cần áp dụng sắp xếp bong bóng nếu chương trình cần chạy trong một môi trường, nơi bộ nhớ rất hạn chế.
Để đo lường mức tiêu thụ tài nguyên của một thuật toán, các chiến lược khác nhau được sử dụng như đã thảo luận trong chương này.
Phân tích tiệm cận
Hành vi tiệm cận của một hàm f(n) đề cập đến sự phát triển của f(n) như n trở nên lớn.
Chúng tôi thường bỏ qua các giá trị nhỏ của n, vì chúng tôi thường quan tâm đến việc ước tính xem chương trình sẽ chậm như thế nào trên các đầu vào lớn.
Một nguyên tắc chung là tốc độ tăng tiệm cận càng chậm thì thuật toán càng tốt. Mặc dù nó không phải lúc nào cũng đúng.
Ví dụ, một thuật toán tuyến tính $f(n) = d * n + k$ luôn luôn tốt hơn một tiệm cận đứng hơn một tiệm cận bậc hai, $f(n) = c.n^2 + q$.
Giải phương trình lặp lại
Sự tái diễn là một phương trình hoặc bất đẳng thức mô tả một hàm theo giá trị của nó trên các đầu vào nhỏ hơn. Các lần lặp lại thường được sử dụng trong mô hình chia để trị.
Hãy để chúng tôi xem xét T(n) là thời gian chạy về vấn đề kích thước n.
Nếu kích thước sự cố đủ nhỏ, hãy nói n < c Ở đâu c là một hằng số, giải pháp đơn giản cần thời gian không đổi, được viết là θ(1). Nếu sự phân chia của bài toán tạo ra một số bài toán con với kích thước$\frac{n}{b}$.
Để giải quyết vấn đề, thời gian cần thiết là a.T(n/b). Nếu chúng ta coi thời gian cần thiết để phân chia làD(n) và thời gian cần thiết để kết hợp các kết quả của các bài toán con là C(n), quan hệ lặp lại có thể được biểu diễn dưới dạng:
$$T(n)=\begin{cases}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\theta(1) & if\:n\leqslant c\\a T(\frac{n}{b})+D(n)+C(n) & otherwise\end{cases}$$
Quan hệ lặp lại có thể được giải quyết bằng cách sử dụng các phương pháp sau:
Substitution Method - Trong phương pháp này, chúng tôi đoán một giới hạn và sử dụng quy nạp toán học, chúng tôi chứng minh rằng giả định của chúng tôi là đúng.
Recursion Tree Method - Trong phương pháp này, một cây lặp lại được hình thành trong đó mỗi nút đại diện cho chi phí.
Master’s Theorem - Đây là một kỹ thuật quan trọng khác để tìm độ phức tạp của quan hệ lặp lại.
Phân tích khấu hao
Phân tích khấu hao thường được sử dụng cho các thuật toán nhất định trong đó một chuỗi các hoạt động tương tự được thực hiện.
Phân tích khấu hao đưa ra ràng buộc về chi phí thực tế của toàn bộ chuỗi hoạt động, thay vì ràng buộc chi phí của chuỗi hoạt động riêng lẻ.
Phân tích khấu hao khác với phân tích trường hợp trung bình; xác suất không liên quan đến phân tích khấu hao. Phân tích khấu hao đảm bảo hiệu suất trung bình của từng hoạt động trong trường hợp xấu nhất.
Nó không chỉ là một công cụ để phân tích mà còn là một cách suy nghĩ về thiết kế, vì thiết kế và phân tích có liên quan chặt chẽ với nhau.
Phương pháp tổng hợp
Phương pháp tổng hợp đưa ra cái nhìn toàn cục về một vấn đề. Trong phương pháp này, nếun hoạt động mất thời gian trong trường hợp xấu nhất T(n)Tổng cộng. Khi đó, chi phí phân bổ của mỗi hoạt động làT(n)/n. Mặc dù các hoạt động khác nhau có thể mất thời gian khác nhau, trong phương pháp này, chi phí khác nhau được bỏ qua.
Phương pháp kế toán
Trong phương pháp này, các khoản phí khác nhau được ấn định cho các nghiệp vụ khác nhau theo chi phí thực tế của chúng. Nếu chi phí khấu hao của một hoạt động vượt quá chi phí thực tế của nó, thì phần chênh lệch đó được gán cho đối tượng như một khoản ghi có. Khoản tín dụng này giúp thanh toán cho các hoạt động sau này mà chi phí khấu hao nhỏ hơn chi phí thực tế.
Nếu chi phí thực tế và chi phí phân bổ của ith hoạt động là $c_{i}$ và $\hat{c_{l}}$, sau đó
$$\displaystyle\sum\limits_{i=1}^n \hat{c_{l}}\geqslant\displaystyle\sum\limits_{i=1}^n c_{i}$$
Phương pháp tiềm năng
Phương pháp này thể hiện công việc trả trước là năng lượng tiềm năng, thay vì coi công việc trả trước là tín dụng. Năng lượng này có thể được giải phóng để chi trả cho các hoạt động sau này.
Nếu chúng tôi thực hiện n hoạt động bắt đầu với cấu trúc dữ liệu ban đầu D0. Hãy để chúng tôi xem xét,ci như chi phí thực tế và Di như cấu trúc dữ liệu của ithhoạt động. Hàm tiềm năng Ф ánh xạ tới một số thực Ф (Di), tiềm năng liên quan của Di. Chi phí khấu hao$\hat{c_{l}}$ có thể được định nghĩa bởi
$$\hat{c_{l}}=c_{i}+\Phi (D_{i})-\Phi (D_{i-1})$$
Do đó, tổng chi phí khấu hao là
$$\displaystyle\sum\limits_{i=1}^n \hat{c_{l}}=\displaystyle\sum\limits_{i=1}^n (c_{i}+\Phi (D_{i})-\Phi (D_{i-1}))=\displaystyle\sum\limits_{i=1}^n c_{i}+\Phi (D_{n})-\Phi (D_{0})$$
Bảng động
Nếu không gian được phân bổ cho bảng không đủ, chúng tôi phải sao chép bảng thành bảng kích thước lớn hơn. Tương tự, nếu số lượng lớn thành viên bị xóa khỏi bảng, bạn nên phân bổ lại bảng với kích thước nhỏ hơn.
Sử dụng phân tích khấu hao, chúng ta có thể chỉ ra rằng chi phí khấu hao của việc chèn và xóa là không đổi và không gian chưa sử dụng trong bảng động không bao giờ vượt quá một phần không đổi của tổng không gian.
Trong chương tiếp theo của hướng dẫn này, chúng ta sẽ thảo luận ngắn gọn về Kí hiệu tiệm cận.
Trong thiết kế Thuật toán, phân tích độ phức tạp của một thuật toán là một khía cạnh thiết yếu. Chủ yếu, độ phức tạp của thuật toán quan tâm đến hiệu suất của nó, tốc độ hoạt động của nó nhanh hay chậm.
Độ phức tạp của một thuật toán mô tả hiệu quả của thuật toán về dung lượng bộ nhớ cần thiết để xử lý dữ liệu và thời gian xử lý.
Độ phức tạp của một thuật toán được phân tích theo hai khía cạnh: Time và Space.
Thời gian phức tạp
Đó là một hàm mô tả lượng thời gian cần thiết để chạy một thuật toán về kích thước của đầu vào. "Thời gian" có thể có nghĩa là số lần truy cập bộ nhớ được thực hiện, số lần so sánh giữa các số nguyên, số lần một số vòng lặp bên trong được thực hiện hoặc một số đơn vị tự nhiên khác liên quan đến lượng thời gian thực mà thuật toán sẽ sử dụng.
Không gian phức tạp
Đó là một hàm mô tả dung lượng bộ nhớ mà một thuật toán sử dụng về kích thước của đầu vào cho thuật toán. Chúng ta thường nói đến bộ nhớ "bổ sung" cần thiết, không tính bộ nhớ cần thiết để lưu trữ dữ liệu đầu vào. Một lần nữa, chúng tôi sử dụng các đơn vị tự nhiên (nhưng độ dài cố định) để đo lường điều này.
Sự phức tạp về không gian đôi khi bị bỏ qua vì không gian được sử dụng là tối thiểu và / hoặc hiển nhiên, tuy nhiên đôi khi nó trở thành một vấn đề quan trọng như thời gian.
Ký hiệu tiệm cận
Thời gian thực thi của một thuật toán phụ thuộc vào tập lệnh, tốc độ bộ xử lý, tốc độ I / O của đĩa, v.v. Do đó, chúng tôi ước tính hiệu quả của một thuật toán theo tiệm cận.
Hàm thời gian của một thuật toán được biểu diễn bằng T(n), Ở đâu n là kích thước đầu vào.
Các loại ký hiệu tiệm cận khác nhau được sử dụng để biểu thị độ phức tạp của một thuật toán. Các ký hiệu tiệm cận sau được sử dụng để tính độ phức tạp thời gian chạy của một thuật toán.
O - Ồ lớn
Ω - Omega lớn
θ - Theta lớn
o - Oh nhỏ
ω - Tiểu omega
O: Đường giới hạn trên của tiệm cận
'O' (Big Oh) là ký hiệu được sử dụng phổ biến nhất. Một chức năngf(n) có thể được đại diện là thứ tự của g(n) đó là O(g(n)), nếu tồn tại một giá trị nguyên dương n như n0 và một hằng số dương c như vậy -
$f(n)\leqslant c.g(n)$ cho $n > n_{0}$ trong mọi trường hợp
Do đó, chức năng g(n) là giới hạn trên cho hàm f(n), như g(n) phát triển nhanh hơn f(n).
Thí dụ
Chúng ta hãy xem xét một hàm đã cho, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$
Đang cân nhắc $g(n) = n^3$,
$f(n)\leqslant 5.g(n)$ cho tất cả các giá trị của $n > 2$
Do đó, sự phức tạp của f(n) có thể được đại diện là $O(g(n))$, I E $O(n^3)$
Ω: Giới hạn dưới tiệm cận
Chúng tôi nói rằng $f(n) = \Omega (g(n))$ khi tồn tại hằng số c cái đó $f(n)\geqslant c.g(n)$ cho tất cả giá trị đủ lớn của n. Đâynlà một số nguyên dương. Nó có nghĩa là chức năngg là giới hạn dưới cho hàm f; sau một giá trị nhất định củan, f sẽ không bao giờ đi xuống dưới g.
Thí dụ
Chúng ta hãy xem xét một hàm đã cho, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$.
Đang cân nhắc $g(n) = n^3$, $f(n)\geqslant 4.g(n)$ cho tất cả các giá trị của $n > 0$.
Do đó, sự phức tạp của f(n) có thể được đại diện là $\Omega (g(n))$, I E $\Omega (n^3)$
θ: Đường giới hạn chặt chẽ tiệm cận
Chúng tôi nói rằng $f(n) = \theta(g(n))$ khi tồn tại các hằng số c1 và c2 cái đó $c_{1}.g(n) \leqslant f(n) \leqslant c_{2}.g(n)$ cho tất cả giá trị đủ lớn của n. Đâyn là một số nguyên dương.
Điều này có nghĩa là chức năng g là một ràng buộc chặt chẽ cho chức năng f.
Thí dụ
Chúng ta hãy xem xét một hàm đã cho, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$
Đang cân nhắc $g(n) = n^3$, $4.g(n) \leqslant f(n) \leqslant 5.g(n)$ cho tất cả các giá trị lớn của n.
Do đó, sự phức tạp của f(n) có thể được đại diện là $\theta (g(n))$, I E $\theta (n^3)$.
O - Ký hiệu
Giới hạn trên của tiệm cận được cung cấp bởi O-notationcó thể chặt chẽ hoặc không tiệm cận. Sự ràng buộc$2.n^2 = O(n^2)$ tiệm cận chặt chẽ, nhưng ràng buộc $2.n = O(n^2)$ không phải.
Chúng tôi sử dụng o-notation để biểu thị một giới hạn trên không chặt chẽ về mặt tiệm cận.
Chúng tôi chính thức xác định o(g(n)) (little-oh of g of n) as the set f(n) = o(g(n)) cho bất kỳ hằng số dương nào $c > 0$ và tồn tại một giá trị $n_{0} > 0$, như vậy mà $0 \leqslant f(n) \leqslant c.g(n)$.
Một cách trực quan, trong o-notation, chức năng f(n) trở nên không đáng kể so với g(n) như ntiếp cận vô cực; đó là,
$$\lim_{n \rightarrow \infty}\left(\frac{f(n)}{g(n)}\right) = 0$$
Thí dụ
Chúng ta hãy xem xét cùng một chức năng, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$
Đang cân nhắc $g(n) = n^{4}$,
$$\lim_{n \rightarrow \infty}\left(\frac{4.n^3 + 10.n^2 + 5.n + 1}{n^4}\right) = 0$$
Do đó, sự phức tạp của f(n) có thể được đại diện là $o(g(n))$, I E $o(n^4)$.
ω - Kí hiệu
Chúng tôi sử dụng ω-notationđể biểu thị một giới hạn dưới không chặt chẽ về mặt tiệm cận. Tuy nhiên, về mặt hình thức, chúng tôi xác địnhω(g(n)) (little-omega of g of n) as the set f(n) = ω(g(n)) cho bất kỳ hằng số dương nào C > 0 và tồn tại một giá trị $n_{0} > 0$, sao cho $ 0 \ leqslant cg (n) <f (n) $.
Ví dụ, $\frac{n^2}{2} = \omega (n)$, nhưng $\frac{n^2}{2} \neq \omega (n^2)$. Mối quan hệ$f(n) = \omega (g(n))$ ngụ ý rằng giới hạn sau tồn tại
$$\lim_{n \rightarrow \infty}\left(\frac{f(n)}{g(n)}\right) = \infty$$
Đó là, f(n) trở nên lớn tùy ý so với g(n) như n tiệm cận vô cùng.
Thí dụ
Chúng ta hãy xem xét cùng một chức năng, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$
Đang cân nhắc $g(n) = n^2$,
$$\lim_{n \rightarrow \infty}\left(\frac{4.n^3 + 10.n^2 + 5.n + 1}{n^2}\right) = \infty$$
Do đó, sự phức tạp của f(n) có thể được đại diện là $o(g(n))$, I E $\omega (n^2)$.
Phân tích Apriori và Apostiari
Phân tích Apriori có nghĩa là, phân tích được thực hiện trước khi chạy nó trên một hệ thống cụ thể. Phân tích này là một giai đoạn trong đó một chức năng được xác định bằng cách sử dụng một số mô hình lý thuyết. Do đó, chúng tôi xác định độ phức tạp về thời gian và không gian của một thuật toán bằng cách chỉ nhìn vào thuật toán thay vì chạy nó trên một hệ thống cụ thể với bộ nhớ, bộ xử lý và trình biên dịch khác.
Phân tích Apostiari của một thuật toán có nghĩa là chúng tôi chỉ thực hiện phân tích một thuật toán sau khi chạy nó trên một hệ thống. Nó trực tiếp phụ thuộc vào hệ thống và thay đổi từ hệ thống này sang hệ thống khác.
Trong một ngành, chúng tôi không thể thực hiện phân tích Apostiari vì phần mềm này thường được tạo cho người dùng ẩn danh, phần mềm này chạy trên một hệ thống khác với những hệ thống hiện có trong ngành.
Trong Apriori, đó là lý do mà chúng tôi sử dụng các ký hiệu tiệm cận để xác định độ phức tạp của thời gian và không gian khi chúng thay đổi từ máy tính này sang máy tính khác; tuy nhiên, về mặt tiệm cận chúng giống nhau.
Trong chương này, chúng ta sẽ thảo luận về độ phức tạp của các bài toán tính toán đối với lượng không gian mà một thuật toán yêu cầu.
Độ phức tạp về không gian chia sẻ nhiều đặc điểm của độ phức tạp về thời gian và là một cách khác để phân loại các vấn đề theo độ khó tính toán của chúng.
Không gian phức tạp là gì?
Độ phức tạp không gian là một hàm mô tả số lượng bộ nhớ (không gian) mà một thuật toán sử dụng về lượng dữ liệu đầu vào cho thuật toán.
Chúng tôi thường nói về extra memorycần thiết, không tính bộ nhớ cần thiết để lưu trữ dữ liệu đầu vào. Một lần nữa, chúng tôi sử dụng các đơn vị tự nhiên (nhưng độ dài cố định) để đo lường điều này.
Chúng ta có thể sử dụng byte, nhưng dễ sử dụng hơn, chẳng hạn như số lượng số nguyên được sử dụng, số lượng cấu trúc có kích thước cố định, v.v.
Cuối cùng, hàm chúng ta đưa ra sẽ độc lập với số byte thực tế cần thiết để biểu diễn đơn vị.
Độ phức tạp về không gian đôi khi bị bỏ qua vì không gian được sử dụng là tối thiểu và / hoặc hiển nhiên, tuy nhiên, đôi khi nó trở thành vấn đề quan trọng như độ phức tạp về thời gian
Định nghĩa
Để cho M là một người xác định Turing machine (TM)điều đó tạm dừng trên tất cả các đầu vào. Không gian phức tạp củaM là chức năng $f \colon N \rightarrow N$, Ở đâu f(n) là số ô tối đa của băng và M quét mọi đầu vào có độ dài M. Nếu không gian phức tạp củaM Là f(n), chúng ta có thể nói về điều đó M chạy trong không gian f(n).
Chúng tôi ước tính độ phức tạp không gian của máy Turing bằng cách sử dụng ký hiệu tiệm cận.
Để cho $f \colon N \rightarrow R^+$là một hàm. Các lớp độ phức tạp không gian có thể được định nghĩa như sau:
SPACE = {L | L is a language decided by an O(f(n)) space deterministic TM}
SPACE = {L | L is a language decided by an O(f(n)) space non-deterministic TM}
PSPACE là lớp ngôn ngữ có thể giải mã trong không gian đa thức trên máy Turing xác định.
Nói cách khác, PSPACE = Uk SPACE (nk)
Định lý Savitch
Một trong những định lý sớm nhất liên quan đến độ phức tạp của không gian là định lý Savitch. Theo định lý này, một máy xác định có thể mô phỏng máy không xác định bằng cách sử dụng một lượng nhỏ không gian.
Đối với độ phức tạp về thời gian, một mô phỏng như vậy dường như yêu cầu thời gian tăng theo cấp số nhân. Đối với độ phức tạp của không gian, định lý này cho thấy rằng bất kỳ máy Turing không xác định nào sử dụngf(n) không gian có thể được chuyển đổi thành một TM xác định sử dụng f2(n) không gian.
Do đó, định lý Savitch nói rằng, đối với bất kỳ hàm nào, $f \colon N \rightarrow R^+$, Ở đâu $f(n) \geqslant n$
NSPACE(f(n)) ⊆ SPACE(f(n))
Mối quan hệ giữa các lớp phức tạp
Sơ đồ sau đây mô tả mối quan hệ giữa các lớp phức tạp khác nhau.

Cho đến nay, chúng ta chưa thảo luận về các lớp P và NP trong hướng dẫn này. Những điều này sẽ được thảo luận sau.
Nhiều thuật toán có bản chất đệ quy để giải quyết một vấn đề đã cho một cách đệ quy xử lý các bài toán con.
Trong divide and conquer approach, một vấn đề được chia thành các vấn đề nhỏ hơn, sau đó các vấn đề nhỏ hơn được giải quyết độc lập, và cuối cùng các giải pháp của các vấn đề nhỏ hơn được kết hợp thành một giải pháp cho vấn đề lớn.
Nói chung, thuật toán chia để trị có ba phần:
Divide the problem thành một số vấn đề con là các trường hợp nhỏ hơn của cùng một vấn đề.
Conquer the sub-problemsbằng cách giải chúng một cách đệ quy. Nếu chúng đủ nhỏ, hãy giải các bài toán con dưới dạng trường hợp cơ sở.
Combine the solutions cho các vấn đề phụ thành giải pháp cho vấn đề ban đầu.
Ưu và nhược điểm của Phương pháp Tiếp cận Chia rẽ và Chinh phục
Cách tiếp cận phân chia và chinh phục ủng hộ sự song song vì các vấn đề phụ là độc lập. Do đó, một thuật toán, được thiết kế bằng kỹ thuật này, có thể chạy đồng thời trên hệ thống đa xử lý hoặc trong các máy khác nhau.
Trong cách tiếp cận này, hầu hết các thuật toán được thiết kế bằng cách sử dụng đệ quy, do đó khả năng quản lý bộ nhớ rất cao. Đối với ngăn xếp hàm đệ quy được sử dụng, nơi trạng thái hàm cần được lưu trữ.
Áp dụng Phương pháp Tiếp cận Chia rẽ và Chinh phục
Sau đây là một số vấn đề, được giải quyết bằng cách sử dụng phương pháp chia và chinh phục.
- Tìm số lớn nhất và nhỏ nhất của một dãy số
- Phép nhân ma trận Strassen
- Hợp nhất sắp xếp
- Tìm kiếm nhị phân
Chúng ta hãy xem xét một vấn đề đơn giản có thể được giải quyết bằng kỹ thuật chia và chinh phục.
Báo cáo vấn đề
Bài toán Max-Min trong phân tích thuật toán là tìm giá trị lớn nhất và nhỏ nhất trong một mảng.
Giải pháp
Để tìm số lớn nhất và số nhỏ nhất trong một mảng nhất định numbers[] có kích thước n, thuật toán sau có thể được sử dụng. Đầu tiên, chúng tôi đại diện chonaive method và sau đó chúng tôi sẽ trình bày divide and conquer approach.
Phương pháp ngây thơ
Phương pháp ngây thơ là một phương pháp cơ bản để giải quyết bất kỳ vấn đề nào. Trong phương pháp này, số tối đa và số tối thiểu có thể được tìm thấy riêng biệt. Để tìm số lớn nhất và số nhỏ nhất, có thể sử dụng thuật toán đơn giản sau.
Algorithm: Max-Min-Element (numbers[])
max := numbers[1]
min := numbers[1]
for i = 2 to n do
if numbers[i] > max then
max := numbers[i]
if numbers[i] < min then
min := numbers[i]
return (max, min)Phân tích
Số lượng so sánh trong phương pháp Naive là 2n - 2.
Có thể giảm số lượng so sánh bằng cách sử dụng phương pháp chia và chinh phục. Sau đây là kỹ thuật.
Cách tiếp cận Phân chia và Chinh phục
Theo cách tiếp cận này, mảng được chia thành hai nửa. Sau đó, sử dụng phương pháp đệ quy số tối đa và tối thiểu trong mỗi nửa được tìm thấy. Sau đó, trả về giá trị lớn nhất của hai cực đại của mỗi nửa và giá trị nhỏ nhất của hai cực tiểu của mỗi nửa.
Trong bài toán đã cho này, số phần tử trong một mảng là $y - x + 1$, Ở đâu y là lớn hơn hoặc bằng x.
$\mathbf{\mathit{Max - Min(x, y)}}$ sẽ trả về giá trị lớn nhất và nhỏ nhất của một mảng $\mathbf{\mathit{numbers[x...y]}}$.
Algorithm: Max - Min(x, y)
if y – x ≤ 1 then
return (max(numbers[x], numbers[y]), min((numbers[x], numbers[y]))
else
(max1, min1):= maxmin(x, ⌊((x + y)/2)⌋)
(max2, min2):= maxmin(⌊((x + y)/2) + 1)⌋,y)
return (max(max1, max2), min(min1, min2))Phân tích
Để cho T(n) là số so sánh được thực hiện bởi $\mathbf{\mathit{Max - Min(x, y)}}$, trong đó số phần tử $n = y - x + 1$.
Nếu T(n) đại diện cho các con số, sau đó quan hệ lặp lại có thể được biểu diễn dưới dạng
$$T(n) = \begin{cases}T\left(\lfloor\frac{n}{2}\rfloor\right)+T\left(\lceil\frac{n}{2}\rceil\right)+2 & for\: n>2\\1 & for\:n = 2 \\0 & for\:n = 1\end{cases}$$
Hãy để chúng tôi giả định rằng n ở dạng quyền lực của 2. Vì thế,n = 2k Ở đâu k là chiều cao của cây đệ quy.
Vì thế,
$$T(n) = 2.T (\frac{n}{2}) + 2 = 2.\left(\begin{array}{c}2.T(\frac{n}{4}) + 2\end{array}\right) + 2 ..... = \frac{3n}{2} - 2$$
So với phương pháp Naïve, trong cách tiếp cận chia để trị, số lượng so sánh ít hơn. Tuy nhiên, sử dụng ký hiệu tiệm cận cả hai cách tiếp cận đều được biểu diễn bằngO(n).
Trong chương này, chúng ta sẽ thảo luận về sắp xếp hợp nhất và phân tích độ phức tạp của nó.
Báo cáo vấn đề
Vấn đề sắp xếp danh sách các số có nghĩa là ngay lập tức với chiến lược chia để trị: chia danh sách thành hai nửa, sắp xếp đệ quy từng nửa, rồi hợp nhất hai danh sách con đã sắp xếp.
Giải pháp
Trong thuật toán này, các số được lưu trữ trong một mảng numbers[]. Đây,p và q đại diện cho chỉ số bắt đầu và kết thúc của một mảng con.
Algorithm: Merge-Sort (numbers[], p, r)
if p < r then
q = ⌊(p + r) / 2⌋
Merge-Sort (numbers[], p, q)
Merge-Sort (numbers[], q + 1, r)
Merge (numbers[], p, q, r)Function: Merge (numbers[], p, q, r)
n1 = q – p + 1
n2 = r – q
declare leftnums[1…n1 + 1] and rightnums[1…n2 + 1] temporary arrays
for i = 1 to n1
leftnums[i] = numbers[p + i - 1]
for j = 1 to n2
rightnums[j] = numbers[q+ j]
leftnums[n1 + 1] = ∞
rightnums[n2 + 1] = ∞
i = 1
j = 1
for k = p to r
if leftnums[i] ≤ rightnums[j]
numbers[k] = leftnums[i]
i = i + 1
else
numbers[k] = rightnums[j]
j = j + 1Phân tích
Chúng ta hãy xem xét, thời gian chạy Merge-Sort là T(n). Vì thế,
$T(n)=\begin{cases}c & if\:n\leqslant 1\\2\:x\:T(\frac{n}{2})+d\:x\:n & otherwise\end{cases}$trong đó c và d là hằng số
Do đó, sử dụng mối quan hệ lặp lại này,
$$T(n) = 2^i T(\frac{n}{2^i}) + i.d.n$$
Như, $i = log\:n,\: T(n) = 2^{log\:n} T(\frac{n}{2^{log\:n}}) + log\:n.d.n$
$=\:c.n + d.n.log\:n$
Vì thế, $T(n) = O(n\:log\:n)$
Thí dụ
Trong ví dụ sau, chúng tôi đã trình bày thuật toán Merge-Sort từng bước. Đầu tiên, mọi mảng lặp được chia thành hai mảng con, cho đến khi mảng con chỉ chứa một phần tử. Khi các mảng con này không thể được chia nhỏ hơn nữa, thì các phép toán hợp nhất được thực hiện.
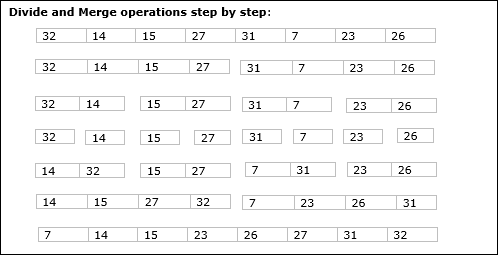
Trong chương này, chúng ta sẽ thảo luận về một thuật toán khác dựa trên phương pháp chia và chinh phục.
Báo cáo vấn đề
Tìm kiếm nhị phân có thể được thực hiện trên một mảng được sắp xếp. Trong cách tiếp cận này, chỉ mục của một phần tửxđược xác định nếu phần tử thuộc danh sách các phần tử. Nếu mảng không được sắp xếp, tìm kiếm tuyến tính được sử dụng để xác định vị trí.
Giải pháp
Trong thuật toán này, chúng tôi muốn tìm liệu phần tử x thuộc về một tập hợp các số được lưu trữ trong một mảng numbers[]. Ở đâul và r đại diện cho chỉ mục bên trái và bên phải của một mảng con mà thao tác tìm kiếm sẽ được thực hiện.
Algorithm: Binary-Search(numbers[], x, l, r)
if l = r then
return l
else
m := ⌊(l + r) / 2⌋
if x ≤ numbers[m] then
return Binary-Search(numbers[], x, l, m)
else
return Binary-Search(numbers[], x, m+1, r)Phân tích
Tìm kiếm tuyến tính chạy trong O(n)thời gian. Trong khi tìm kiếm nhị phân tạo ra kết quả trongO(log n) thời gian
Để cho T(n) là số so sánh trong trường hợp xấu nhất trong một mảng n các yếu tố.
Vì thế,
$$T(n)=\begin{cases}0 & if\:n= 1\\T(\frac{n}{2})+1 & otherwise\end{cases}$$
Sử dụng mối quan hệ lặp lại này $T(n) = log\:n$.
Do đó, tìm kiếm nhị phân sử dụng $O(log\:n)$ thời gian.
Thí dụ
Trong ví dụ này, chúng ta sẽ tìm kiếm phần tử 63.

Trong chương này, trước tiên chúng ta sẽ thảo luận về phương pháp tổng quát của phép nhân ma trận và sau đó chúng ta sẽ thảo luận về thuật toán nhân ma trận của Strassen.
Báo cáo vấn đề
Chúng ta hãy xem xét hai ma trận X và Y. Chúng tôi muốn tính toán ma trận kết quảZ bằng cách nhân X và Y.
Phương pháp ngây thơ
Đầu tiên, chúng ta sẽ thảo luận về phương pháp ngây thơ và sự phức tạp của nó. Ở đây, chúng tôi đang tính toánZ = X × Y. Sử dụng phương pháp Naïve, hai ma trận (X và Y) có thể được nhân lên nếu thứ tự của các ma trận này là p × q và q × r. Sau đây là thuật toán.
Algorithm: Matrix-Multiplication (X, Y, Z)
for i = 1 to p do
for j = 1 to r do
Z[i,j] := 0
for k = 1 to q do
Z[i,j] := Z[i,j] + X[i,k] × Y[k,j]Phức tạp
Ở đây, chúng tôi giả định rằng các phép toán số nguyên có O(1)thời gian. Có baforvòng lặp trong thuật toán này và một vòng lặp được lồng trong thuật toán khác. Do đó, thuật toán mấtO(n3) thời gian để thực hiện.
Thuật toán nhân ma trận của Strassen
Trong bối cảnh này, sử dụng thuật toán nhân Ma trận của Strassen, mức tiêu thụ thời gian có thể được cải thiện một chút.
Phép nhân Ma trận Strassen chỉ có thể được thực hiện trên square matrices Ở đâu n là một power of 2. Thứ tự của cả hai ma trận làn × n.
Chia X, Y và Z thành bốn (n / 2) × (n / 2) ma trận như được biểu diễn dưới đây -
$Z = \begin{bmatrix}I & J \\K & L \end{bmatrix}$ $X = \begin{bmatrix}A & B \\C & D \end{bmatrix}$ và $Y = \begin{bmatrix}E & F \\G & H \end{bmatrix}$
Sử dụng Thuật toán Strassen tính toán những điều sau:
$$M_{1} \: \colon= (A+C) \times (E+F)$$
$$M_{2} \: \colon= (B+D) \times (G+H)$$
$$M_{3} \: \colon= (A-D) \times (E+H)$$
$$M_{4} \: \colon= A \times (F-H)$$
$$M_{5} \: \colon= (C+D) \times (E)$$
$$M_{6} \: \colon= (A+B) \times (H)$$
$$M_{7} \: \colon= D \times (G-E)$$
Sau đó,
$$I \: \colon= M_{2} + M_{3} - M_{6} - M_{7}$$
$$J \: \colon= M_{4} + M_{6}$$
$$K \: \colon= M_{5} + M_{7}$$
$$L \: \colon= M_{1} - M_{3} - M_{4} - M_{5}$$
Phân tích
$T(n)=\begin{cases}c & if\:n= 1\\7\:x\:T(\frac{n}{2})+d\:x\:n^2 & otherwise\end{cases}$trong đó c và d là hằng số
Sử dụng mối quan hệ lặp lại này, chúng tôi nhận được $T(n) = O(n^{log7})$
Do đó, độ phức tạp của thuật toán nhân ma trận Strassen là $O(n^{log7})$.
Trong số tất cả các phương pháp tiếp cận theo thuật toán, cách tiếp cận đơn giản và dễ hiểu nhất là phương pháp Tham lam. Trong cách tiếp cận này, quyết định được đưa ra dựa trên thông tin hiện có sẵn mà không cần lo lắng về ảnh hưởng của quyết định hiện tại trong tương lai.
Các thuật toán tham lam xây dựng giải pháp từng phần một, chọn phần tiếp theo theo cách sao cho nó mang lại lợi ích ngay lập tức. Cách tiếp cận này không bao giờ xem xét lại các lựa chọn đã thực hiện trước đó. Cách tiếp cận này chủ yếu được sử dụng để giải quyết các vấn đề tối ưu hóa. Phương pháp tham lam rất dễ thực hiện và khá hiệu quả trong hầu hết các trường hợp. Do đó, chúng ta có thể nói rằng thuật toán Greedy là một mô hình thuật toán dựa trên heuristic tuân theo lựa chọn tối ưu cục bộ ở mỗi bước với hy vọng tìm ra giải pháp tối ưu toàn cục.
Trong nhiều bài toán, nó không tạo ra một giải pháp tối ưu mặc dù nó đưa ra một giải pháp gần đúng (gần tối ưu) trong một thời gian hợp lý.
Các thành phần của thuật toán tham lam
Thuật toán tham lam có năm thành phần sau:
A candidate set - Một giải pháp được tạo ra từ bộ này.
A selection function - Được sử dụng để chọn ứng viên tốt nhất được thêm vào giải pháp.
A feasibility function - Được sử dụng để xác định xem một ứng viên có thể được sử dụng để đóng góp vào giải pháp hay không.
An objective function - Dùng để gán giá trị cho một giải pháp hoặc một giải pháp từng phần.
A solution function - Được sử dụng để chỉ ra liệu đã đạt được một giải pháp hoàn chỉnh hay chưa.
Lĩnh vực ứng dụng
Cách tiếp cận tham lam được sử dụng để giải quyết nhiều vấn đề, chẳng hạn như
Tìm đường đi ngắn nhất giữa hai đỉnh bằng thuật toán Dijkstra.
Tìm cây bao trùm tối thiểu trong biểu đồ bằng thuật toán của Prim / Kruskal, v.v.
Khi Phương pháp tiếp cận Tham lam thất bại
Trong nhiều bài toán, thuật toán Tham lam không tìm được giải pháp tối ưu, hơn nữa nó có thể tạo ra giải pháp tồi tệ nhất. Không thể giải quyết các vấn đề như Người bán hàng đi du lịch và Knapsack bằng cách sử dụng phương pháp này.
Thuật toán Tham lam có thể được hiểu rất rõ ràng với một bài toán nổi tiếng được gọi là bài toán Knapsack. Mặc dù vấn đề tương tự có thể được giải quyết bằng cách sử dụng các cách tiếp cận thuật toán khác, nhưng cách tiếp cận Greedy giải quyết vấn đề Fractional Knapsack một cách hợp lý trong một thời gian thích hợp. Hãy để chúng tôi thảo luận chi tiết về vấn đề Knapsack.
Vấn đề về Knapsack
Cho một tập hợp các mục, mỗi mục có trọng lượng và giá trị, hãy xác định một tập hợp con các mục để đưa vào một bộ sưu tập sao cho tổng trọng lượng nhỏ hơn hoặc bằng một giới hạn nhất định và tổng giá trị càng lớn càng tốt.
Bài toán knapsack nằm trong bài toán tối ưu hóa tổ hợp. Nó xuất hiện như một bài toán con trong nhiều mô hình toán học phức tạp hơn của các bài toán trong thế giới thực. Một cách tiếp cận chung cho các vấn đề khó khăn là xác định ràng buộc hạn chế nhất, bỏ qua những hạn chế khác, giải quyết một vấn đề khó khăn và bằng cách nào đó điều chỉnh giải pháp để thỏa mãn các hạn chế bị bỏ qua.
Các ứng dụng
Trong nhiều trường hợp phân bổ tài nguyên cùng với một số ràng buộc, vấn đề có thể được phát sinh theo cách tương tự của vấn đề Knapsack. Sau đây là một số ví dụ.
- Tìm cách ít lãng phí nhất để cắt giảm nguyên liệu thô
- tối ưu hóa danh mục đầu tư
- Cắt giảm vấn đề tồn kho
Tình huống sự cố
Một tên trộm đang cướp một cửa hàng và có thể mang theo khối lượng tối đa là Wvào ba lô của mình. Có n mặt hàng có sẵn trong cửa hàng và trọng lượng củaith mục là wi và lợi nhuận của nó là pi. Kẻ trộm nên lấy những vật dụng gì?
Trong bối cảnh này, các vật phẩm nên được chọn sao cho tên trộm sẽ mang theo những vật phẩm đó mà hắn sẽ thu được lợi nhuận tối đa. Do đó, mục tiêu của kẻ trộm là tối đa hóa lợi nhuận.
Dựa trên bản chất của các mặt hàng, các vấn đề về Knapsack được phân loại thành
- Fractional Knapsack
- Knapsack
Fractional Knapsack
Trong trường hợp này, các vật phẩm có thể bị chia thành nhiều phần nhỏ hơn, do đó kẻ trộm có thể chọn các phần nhỏ của vật phẩm.
Theo báo cáo vấn đề,
Có n các mặt hàng trong cửa hàng
Trọng lượng của ith mục $w_{i} > 0$
Lợi nhuận cho ith mục $p_{i} > 0$ và
Dung lượng của Knapsack là W
Trong phiên bản này của vấn đề Knapsack, các mục có thể được chia thành nhiều mảnh nhỏ hơn. Vì vậy, kẻ trộm có thể chỉ mất một phần nhỏxi của ith mục.
$$0 \leqslant x_{i} \leqslant 1$$
Các ith mục đóng góp trọng lượng $x_{i}.w_{i}$ đến tổng trọng lượng trong túi và lợi nhuận $x_{i}.p_{i}$ vào tổng lợi nhuận.
Do đó, mục tiêu của thuật toán này là
$$maximize\:\displaystyle\sum\limits_{n=1}^n (x_{i}.p_{}i)$$
chịu sự ràng buộc,
$$\displaystyle\sum\limits_{n=1}^n (x_{i}.w_{}i) \leqslant W$$
Rõ ràng là một giải pháp tối ưu phải lấp đầy chính xác cái túi, nếu không chúng ta có thể thêm một phần nhỏ của một trong những mục còn lại và tăng lợi nhuận tổng thể.
Do đó, một giải pháp tối ưu có thể đạt được bằng cách
$$\displaystyle\sum\limits_{n=1}^n (x_{i}.w_{}i) = W$$
Trong bối cảnh này, trước tiên chúng ta cần sắp xếp các mục đó theo giá trị của $\frac{p_{i}}{w_{i}}$, vậy nên $\frac{p_{i}+1}{w_{i}+1}$ ≤ $\frac{p_{i}}{w_{i}}$. Đây,x là một mảng để lưu trữ phần nhỏ của các mục.
Algorithm: Greedy-Fractional-Knapsack (w[1..n], p[1..n], W)
for i = 1 to n
do x[i] = 0
weight = 0
for i = 1 to n
if weight + w[i] ≤ W then
x[i] = 1
weight = weight + w[i]
else
x[i] = (W - weight) / w[i]
weight = W
break
return xPhân tích
Nếu các mục được cung cấp đã được sắp xếp theo thứ tự giảm dần $\mathbf{\frac{p_{i}}{w_{i}}}$, sau đó whileloop mất một thời gian trong O(n); Do đó, tổng thời gian bao gồm cả việc sắp xếp là trongO(n logn).
Thí dụ
Chúng ta hãy xem xét rằng dung lượng của chiếc túi W = 60 và danh sách các mặt hàng được cung cấp được hiển thị trong bảng sau:
| Mục | A | B | C | D |
|---|---|---|---|---|
| Lợi nhuận | 280 | 100 | 120 | 120 |
| Cân nặng | 40 | 10 | 20 | 24 |
| Tỉ lệ $(\frac{p_{i}}{w_{i}})$ | 7 | 10 | 6 | 5 |
Vì các mặt hàng đã cung cấp không được sắp xếp dựa trên $\mathbf{\frac{p_{i}}{w_{i}}}$. Sau khi phân loại, các mục như trong bảng sau.
| Mục | B | A | C | D |
|---|---|---|---|---|
| Lợi nhuận | 100 | 280 | 120 | 120 |
| Cân nặng | 10 | 40 | 20 | 24 |
| Tỉ lệ $(\frac{p_{i}}{w_{i}})$ | 10 | 7 | 6 | 5 |
Giải pháp
Sau khi phân loại tất cả các mục theo $\frac{p_{i}}{w_{i}}$. Trước hếtB được chọn làm trọng lượng của Bnhỏ hơn dung lượng của cái túi. Mục tiếp theoA được chọn, vì dung lượng khả dụng của bao lớn hơn trọng lượng của A. Hiện nay,Cđược chọn làm mục tiếp theo. Tuy nhiên, không thể chọn toàn bộ mục vì dung lượng còn lại của bao nhỏ hơn trọng lượng củaC.
Do đó, một phần của C (tức là (60 - 50) / 20) được chọn.
Bây giờ, sức chứa của Knapsack bằng với các mục đã chọn. Do đó, không thể chọn mục nào nữa.
Tổng trọng lượng của các mục đã chọn là 10 + 40 + 20 * (10/20) = 60
Và tổng lợi nhuận là 100 + 280 + 120 * (10/20) = 380 + 60 = 440
Đây là giải pháp tối ưu. Chúng tôi không thể thu được nhiều lợi nhuận hơn khi chọn bất kỳ sự kết hợp khác nhau của các mặt hàng.
Báo cáo vấn đề
Trong bài toán sắp xếp công việc, mục tiêu là tìm ra một chuỗi các công việc được hoàn thành trong thời hạn và mang lại lợi nhuận tối đa.
Giải pháp
Hãy để chúng tôi xem xét, một bộ nđược giao những công việc gắn liền với thời hạn và lợi nhuận thu được, nếu một công việc được hoàn thành trước thời hạn của nó. Những công việc này cần được sắp xếp theo cách có lợi nhuận tối đa.
Có thể xảy ra rằng tất cả các công việc được giao có thể không được hoàn thành trong thời hạn của chúng.
Giả sử, thời hạn của ith việc làm Ji Là di và lợi nhuận nhận được từ công việc này là pi. Do đó, giải pháp tối ưu của thuật toán này là một giải pháp khả thi với lợi nhuận tối đa.
Vì vậy, $D(i) > 0$ cho $1 \leqslant i \leqslant n$.
Ban đầu, những công việc này được sắp xếp theo lợi nhuận, tức là $p_{1} \geqslant p_{2} \geqslant p_{3} \geqslant \:... \: \geqslant p_{n}$.
Algorithm: Job-Sequencing-With-Deadline (D, J, n, k)
D(0) := J(0) := 0
k := 1
J(1) := 1 // means first job is selected
for i = 2 … n do
r := k
while D(J(r)) > D(i) and D(J(r)) ≠ r do
r := r – 1
if D(J(r)) ≤ D(i) and D(i) > r then
for l = k … r + 1 by -1 do
J(l + 1) := J(l)
J(r + 1) := i
k := k + 1Phân tích
Trong thuật toán này, chúng tôi đang sử dụng hai vòng lặp, một vòng lặp nằm trong một vòng lặp khác. Do đó, độ phức tạp của thuật toán này là$O(n^2)$.
Thí dụ
Chúng ta hãy xem xét một tập hợp các công việc đã cho như thể hiện trong bảng sau. Chúng tôi phải tìm ra một chuỗi các công việc, những công việc này sẽ được hoàn thành trong thời hạn và sẽ mang lại lợi nhuận tối đa. Mỗi công việc gắn liền với thời hạn và lợi nhuận.
| Việc làm | J1 | J2 | J3 | J4 | J5 |
|---|---|---|---|---|---|
| Hạn chót | 2 | 1 | 3 | 2 | 1 |
| Lợi nhuận | 60 | 100 | 20 | 40 | 20 |
Giải pháp
Để giải quyết vấn đề này, các công việc đã cho được sắp xếp theo lợi nhuận của chúng theo thứ tự giảm dần. Do đó, sau khi sắp xếp, các công việc được sắp xếp như trong bảng sau.
| Việc làm | J2 | J1 | J4 | J3 | J5 |
|---|---|---|---|---|---|
| Hạn chót | 1 | 2 | 2 | 3 | 1 |
| Lợi nhuận | 100 | 60 | 40 | 20 | 20 |
Từ nhóm công việc này, trước tiên chúng tôi chọn J2, vì nó có thể được hoàn thành trong thời hạn và đóng góp lợi nhuận tối đa.
Kế tiếp, J1 được chọn vì nó mang lại nhiều lợi nhuận hơn so với J4.
Trong đồng hồ tiếp theo, J4 không thể được chọn vì thời hạn của nó đã hết, do đó J3 được chọn khi nó thực thi trong thời hạn của nó.
Công việc J5 bị loại bỏ vì nó không thể được thực thi trong thời hạn của nó.
Do đó, giải pháp là chuỗi các công việc (J2, J1, J3), đang được thực hiện trong thời hạn và mang lại lợi nhuận tối đa.
Tổng lợi nhuận của chuỗi này là 100 + 60 + 20 = 180.
Hợp nhất một tập hợp các tệp được sắp xếp có độ dài khác nhau thành một tệp được sắp xếp duy nhất. Chúng tôi cần tìm một giải pháp tối ưu, nơi tệp kết quả sẽ được tạo trong thời gian tối thiểu.
Nếu số lượng tệp được sắp xếp được cung cấp, có nhiều cách để hợp nhất chúng thành một tệp được sắp xếp duy nhất. Sự hợp nhất này có thể được thực hiện theo cặp khôn ngoan. Do đó, kiểu hợp nhất này được gọi là2-way merge patterns.
Vì các quá trình ghép nối khác nhau yêu cầu lượng thời gian khác nhau, trong chiến lược này, chúng tôi muốn xác định một cách tối ưu để hợp nhất nhiều tệp với nhau. Tại mỗi bước, hai chuỗi ngắn nhất được hợp nhất.
Để hợp nhất một p-record file và một q-record file yêu cầu có thể p + q kỷ lục di chuyển, lựa chọn rõ ràng là, hợp nhất hai tệp nhỏ nhất với nhau ở mỗi bước.
Các mẫu hợp nhất hai chiều có thể được biểu diễn bằng cây hợp nhất nhị phân. Hãy để chúng tôi xem xét một tập hợpn các tệp được sắp xếp {f1, f2, f3, …, fn}. Ban đầu, mỗi phần tử này được coi là một cây nhị phân nút đơn. Để tìm giải pháp tối ưu này, thuật toán sau được sử dụng.
Algorithm: TREE (n)
for i := 1 to n – 1 do
declare new node
node.leftchild := least (list)
node.rightchild := least (list)
node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight)
insert (list, node);
return least (list);Khi kết thúc thuật toán này, trọng số của nút gốc đại diện cho chi phí tối ưu.
Thí dụ
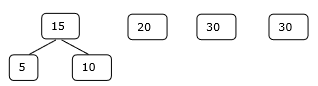
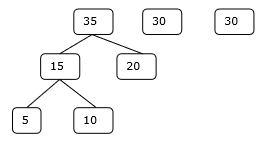
Ta xét các tập đã cho, f 1 , f 2 , f 3 , f 4 và f 5 có số phần tử lần lượt là 20, 30, 10, 5 và 30.
Nếu các hoạt động hợp nhất được thực hiện theo trình tự được cung cấp, thì
M1 = merge f1 and f2 => 20 + 30 = 50
M2 = merge M1 and f3 => 50 + 10 = 60
M3 = merge M2 and f4 => 60 + 5 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Do đó, tổng số hoạt động là
50 + 60 + 65 + 95 = 270
Bây giờ, câu hỏi đặt ra là có giải pháp nào tốt hơn không?
Sắp xếp các số theo kích thước của chúng theo thứ tự tăng dần, chúng tôi nhận được chuỗi sau:
f4, f3, f1, f2, f5
Do đó, các hoạt động hợp nhất có thể được thực hiện trên trình tự này
M1 = merge f4 and f3 => 5 + 10 = 15
M2 = merge M1 and f1 => 15 + 20 = 35
M3 = merge M2 and f2 => 35 + 30 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Do đó, tổng số hoạt động là
15 + 35 + 65 + 95 = 210
Rõ ràng, cái này tốt hơn cái trước.
Trong bối cảnh này, bây giờ chúng ta sẽ giải quyết vấn đề bằng cách sử dụng thuật toán này.
Bộ ban đầu

Bước 1
Bước 2
Bước 3
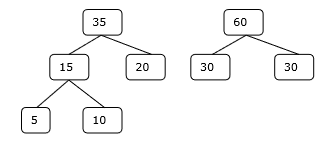
Bước 4
Do đó, giải pháp có 15 + 35 + 60 + 95 = 205 số so sánh.
Lập trình động cũng được sử dụng trong các bài toán tối ưu hóa. Giống như phương pháp chia để trị, Lập trình động giải quyết các vấn đề bằng cách kết hợp các giải pháp của các bài toán con. Hơn nữa, thuật toán Lập trình động giải quyết mỗi vấn đề con chỉ một lần và sau đó lưu câu trả lời của nó trong một bảng, do đó tránh phải tính toán lại câu trả lời mỗi lần.
Hai thuộc tính chính của một vấn đề gợi ý rằng vấn đề đã cho có thể được giải quyết bằng cách sử dụng Lập trình động. Các thuộc tính này làoverlapping sub-problems and optimal substructure.
Các vấn đề phụ chồng chéo
Tương tự như cách tiếp cận Phân chia và Chinh phục, Lập trình động cũng kết hợp các giải pháp cho các vấn đề phụ. Nó chủ yếu được sử dụng khi cần lặp đi lặp lại giải pháp của một vấn đề phụ. Các giải pháp đã tính toán được lưu trữ trong một bảng, do đó chúng không cần phải tính toán lại. Do đó, kỹ thuật này là cần thiết khi tồn tại vấn đề con chồng chéo.
Ví dụ: Tìm kiếm nhị phân không có vấn đề phụ chồng chéo. Trong khi chương trình đệ quy các số Fibonacci có nhiều vấn đề con trùng lặp.
Cấu trúc con tối ưu
Một bài toán đã cho có Thuộc tính cấu trúc con tối ưu, nếu phương án tối ưu của bài toán đã cho có thể thu được bằng cách sử dụng các lời giải tối ưu của các bài toán con của nó.
Ví dụ, bài toán Đường đi ngắn nhất có thuộc tính cấu trúc con tối ưu sau:
Nếu một nút x nằm trong đường dẫn ngắn nhất từ nút nguồn u đến nút đích v, sau đó là con đường ngắn nhất từ u đến v là sự kết hợp của con đường ngắn nhất từ u đến xvà con đường ngắn nhất từ x đến v.
Các thuật toán đường dẫn ngắn nhất theo cặp tiêu chuẩn như Floyd-Warshall và Bellman-Ford là những ví dụ điển hình về Lập trình động.
Các bước của phương pháp tiếp cận lập trình động
Thuật toán lập trình động được thiết kế theo bốn bước sau:
- Đặc trưng cho cấu trúc của một giải pháp tối ưu.
- Xác định đệ quy giá trị của một giải pháp tối ưu.
- Tính toán giá trị của một giải pháp tối ưu, thường theo kiểu từ dưới lên.
- Xây dựng một giải pháp tối ưu từ thông tin được tính toán.
Các ứng dụng của phương pháp tiếp cận lập trình động
- Phép nhân chuỗi ma trận
- Trình tự con chung dài nhất
- Vấn đề nhân viên bán hàng đi du lịch
Trong hướng dẫn này, trước đó chúng ta đã thảo luận về vấn đề Fractional Knapsack bằng cách sử dụng cách tiếp cận Tham lam. Chúng tôi đã chỉ ra rằng cách tiếp cận Tham lam mang lại giải pháp tối ưu cho Fractional Knapsack. Tuy nhiên, chương này sẽ đề cập đến vấn đề Knapsack 0-1 và phân tích của nó.
Trong 0-1 Knapsack, các vật phẩm không thể bị phá vỡ, có nghĩa là kẻ trộm nên lấy toàn bộ hoặc nên bỏ lại. Đây là lý do đằng sau việc gọi nó là 0-1 Knapsack.
Do đó, trong trường hợp 0-1 Knapsack, giá trị của xi có thể là một trong hai 0 hoặc là 1, trong đó các ràng buộc khác được giữ nguyên.
0-1 Knapsack không thể được giải quyết bằng cách tiếp cận Tham lam. Cách tiếp cận tham lam không đảm bảo một giải pháp tối ưu. Trong nhiều trường hợp, cách tiếp cận Tham lam có thể đưa ra giải pháp tối ưu.
Các ví dụ sau đây sẽ thiết lập tuyên bố của chúng tôi.
Ví dụ 1
Chúng ta hãy coi rằng công suất của cái túi là W = 25 và các mục như trong bảng sau.
| Mục | A | B | C | D |
|---|---|---|---|---|
| Lợi nhuận | 24 | 18 | 18 | 10 |
| Cân nặng | 24 | 10 | 10 | 7 |
Không tính đến lợi nhuận trên một đơn vị trọng lượng (pi/wi), nếu chúng ta áp dụng cách tiếp cận Tham lam để giải quyết vấn đề này, mục đầu tiên Asẽ được lựa chọn vì nó sẽ góp phần tối đa i mẹ lợi nhuận trong số tất cả các yếu tố.
Sau khi chọn mặt hàng A, sẽ không có mục nào được chọn. Do đó, đối với nhóm mục nhất định này, tổng lợi nhuận là24. Trong khi đó, giải pháp tối ưu có thể đạt được bằng cách chọn các mục,B và C, trong đó tổng lợi nhuận là 18 + 18 = 36.
Ví dụ-2
Thay vì chọn các mục dựa trên lợi ích tổng thể, trong ví dụ này, các mục được chọn dựa trên tỷ lệ p i / w i . Chúng ta hãy coi rằng công suất của cái knaps là W = 60 và các mục như trong bảng sau.
| Mục | A | B | C |
|---|---|---|---|
| Giá bán | 100 | 280 | 120 |
| Cân nặng | 10 | 40 | 20 |
| Tỉ lệ | 10 | 7 | 6 |
Sử dụng cách tiếp cận Tham lam, mục đầu tiên Ađã được chọn. Sau đó, mục tiếp theoBlà lựa chọn. Do đó, tổng lợi nhuận là100 + 280 = 380. Tuy nhiên, giải pháp tối ưu của trường hợp này có thể đạt được bằng cách chọn các mục,B và C, tổng lợi nhuận là 280 + 120 = 400.
Do đó, có thể kết luận rằng cách tiếp cận Tham lam có thể không đưa ra giải pháp tối ưu.
Để giải quyết 0-1 Knapsack, cần có phương pháp Lập trình động.
Báo cáo vấn đề
Một tên trộm đang cướp một cửa hàng và có thể mang theo trọng lượng tối đa của tôi làWvào ba lô của mình. Cón vật phẩm và trọng lượng của ith mục là wi và lợi nhuận của việc chọn mặt hàng này là pi. Kẻ trộm nên lấy những vật dụng gì?
Phương pháp tiếp cận lập trình động
Để cho i trở thành mục được đánh số cao nhất trong một giải pháp tối ưu S cho WUSD. Sau đóS' = S - {i} là một giải pháp tối ưu cho W - wi đô la và giá trị của giải pháp S Là Vi cộng với giá trị của bài toán con.
Chúng ta có thể diễn đạt thực tế này trong công thức sau: c[i, w] trở thành giải pháp cho các mặt hàng 1,2, … , ivà trọng lượng mẹ tôi tối đaw.
Thuật toán nhận các đầu vào sau
Max i cân mẹW
Số lượng mặt hàng n
Hai chuỗi v = <v1, v2, …, vn> và w = <w1, w2, …, wn>
Dynamic-0-1-knapsack (v, w, n, W)
for w = 0 to W do
c[0, w] = 0
for i = 1 to n do
c[i, 0] = 0
for w = 1 to W do
if wi ≤ w then
if vi + c[i-1, w-wi] then
c[i, w] = vi + c[i-1, w-wi]
else c[i, w] = c[i-1, w]
else
c[i, w] = c[i-1, w]Tập hợp các mục cần lấy có thể được suy ra từ bảng, bắt đầu từ c[n, w] và truy ngược lại nơi xuất phát các giá trị tối ưu.
Nếu c [i, w] = c [i-1, w] , thì mụci không phải là một phần của giải pháp và chúng tôi tiếp tục theo dõi c[i-1, w]. Nếu không, mụci là một phần của giải pháp và chúng tôi tiếp tục theo dõi c[i-1, w-W].
Phân tích
Thuật toán này cần θ ( n , w ) lần vì bảng c có ( n + 1). ( W + 1) mục nhập, trong đó mỗi mục nhập yêu cầu θ (1) thời gian để tính toán.
Vấn đề về dãy con phổ biến dài nhất là tìm dãy dài nhất tồn tại trong cả hai chuỗi đã cho.
Trình tự con
Chúng ta hãy xem xét một dãy S = <s 1 , s 2 , s 3 , s 4 ,…, s n >.
Dãy Z = <z 1 , z 2 , z 3 , z 4 ,…, z m > trên S được gọi là dãy con của S, nếu và chỉ khi nó có thể được suy ra từ việc xóa S của một số phần tử.
Trình tự con chung
Giả sử, X và Ylà hai chuỗi trên một tập hợp hữu hạn các phần tử. Chúng ta có thể nói về điều đóZ là một dãy con chung của X và Y, nếu Z là một con của cả hai X và Y.
Trình tự con chung dài nhất
Nếu một tập hợp các trình tự được cho trước, vấn đề dãy con chung dài nhất là tìm một dãy con chung của tất cả các dãy có độ dài tối đa.
Bài toán con phổ biến dài nhất là một bài toán khoa học máy tính cổ điển, là cơ sở của các chương trình so sánh dữ liệu như tiện ích khác biệt, và có các ứng dụng trong tin sinh học. Nó cũng được sử dụng rộng rãi bởi các hệ thống kiểm soát sửa đổi, chẳng hạn như SVN và Git, để điều chỉnh nhiều thay đổi được thực hiện đối với bộ sưu tập tệp được kiểm soát bởi phiên bản.
Phương pháp ngây thơ
Để cho X là một chuỗi độ dài m và Y một chuỗi chiều dài n. Kiểm tra mọi phần sau củaX cho dù nó là một dãy con của Yvà trả về dãy con chung dài nhất được tìm thấy.
Có 2m chuỗi con của X. Kiểm tra các trình tự xem nó có phải là một chuỗi con củaY nhận O(n)thời gian. Do đó, thuật toán ngây thơ sẽ lấyO(n2m) thời gian.
Lập trình năng động
Gọi X = <x 1 , x 2 , x 3 ,…, x m > và Y = <y 1 , y 2 , y 3 ,…, y n > là các dãy. Để tính độ dài của một phần tử, thuật toán sau được sử dụng.
Trong quy trình này, bảng C[m, n] được tính theo thứ tự chính của hàng và một bảng khác B[m,n] được tính toán để tạo ra giải pháp tối ưu.
Algorithm: LCS-Length-Table-Formulation (X, Y)
m := length(X)
n := length(Y)
for i = 1 to m do
C[i, 0] := 0
for j = 1 to n do
C[0, j] := 0
for i = 1 to m do
for j = 1 to n do
if xi = yj
C[i, j] := C[i - 1, j - 1] + 1
B[i, j] := ‘D’
else
if C[i -1, j] ≥ C[i, j -1]
C[i, j] := C[i - 1, j] + 1
B[i, j] := ‘U’
else
C[i, j] := C[i, j - 1]
B[i, j] := ‘L’
return C and BAlgorithm: Print-LCS (B, X, i, j)
if i = 0 and j = 0
return
if B[i, j] = ‘D’
Print-LCS(B, X, i-1, j-1)
Print(xi)
else if B[i, j] = ‘U’
Print-LCS(B, X, i-1, j)
else
Print-LCS(B, X, i, j-1)Thuật toán này sẽ in ra dãy con chung dài nhất của X và Y.
Phân tích
Để điền bảng, bên ngoài for lặp lại vòng lặp m thời gian và bên trong for lặp lại vòng lặp nlần. Do đó, độ phức tạp của thuật toán là O (m, n) , trong đóm và n là độ dài của hai chuỗi.
Thí dụ
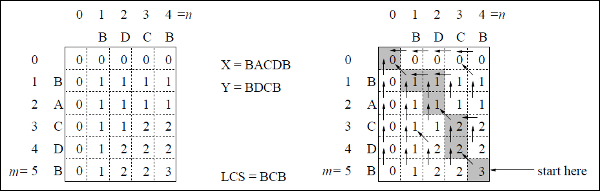
Trong ví dụ này, chúng tôi có hai chuỗi X = BACDB và Y = BDCB để tìm dãy con chung dài nhất.
Theo thuật toán LCS-Độ dài-Bảng-Công thức (như đã nêu ở trên), chúng ta đã tính được bảng C (được hiển thị ở phía bên trái) và bảng B (được hiển thị ở phía bên phải).
Trong bảng B, thay vì 'D', 'L' và 'U', chúng tôi sử dụng mũi tên chéo, mũi tên trái và mũi tên lên tương ứng. Sau khi tạo bảng B, LCS được xác định bởi chức năng LCS-Print. Kết quả là BCB.
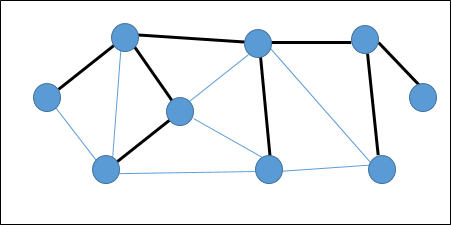
A spanning tree là một tập con của một Đồ thị vô hướng có tất cả các đỉnh được nối với nhau bằng số cạnh tối thiểu.
Nếu tất cả các đỉnh được kết nối trong một đồ thị, thì tồn tại ít nhất một cây khung. Trong một biểu đồ, có thể tồn tại nhiều hơn một cây khung.
Tính chất
- Cây bao trùm không có bất kỳ chu trình nào.
- Có thể đạt được bất kỳ đỉnh nào từ bất kỳ đỉnh nào khác.
Thí dụ
Trong biểu đồ sau, các cạnh được đánh dấu tạo thành một cây bao trùm.
Cây kéo dài tối thiểu
A Minimum Spanning Tree (MST)là một tập con các cạnh của một đồ thị vô hướng có trọng số được liên thông nối tất cả các đỉnh với nhau với tổng trọng số cạnh nhỏ nhất có thể. Để lấy MST, có thể sử dụng thuật toán Prim hoặc thuật toán Kruskal. Do đó, chúng ta sẽ thảo luận về thuật toán của Prim trong chương này.
Như chúng ta đã thảo luận, một biểu đồ có thể có nhiều hơn một cây bao trùm. Nếu cón số đỉnh, cây bao trùm phải có n - 1số cạnh. Trong bối cảnh này, nếu mỗi cạnh của đồ thị được liên kết với một trọng số và tồn tại nhiều hơn một cây bao trùm, chúng ta cần tìm cây bao trùm nhỏ nhất của đồ thị.
Hơn nữa, nếu tồn tại bất kỳ cạnh có trọng số trùng lặp nào, biểu đồ có thể có nhiều cây khung tối thiểu.
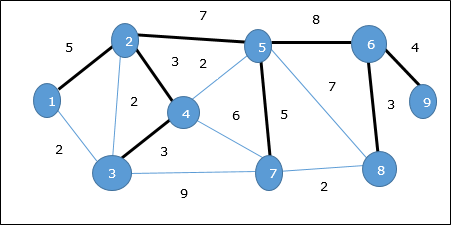
Trong biểu đồ trên, chúng ta đã chỉ ra một cây bao trùm mặc dù nó không phải là cây bao trùm tối thiểu. Chi phí của cây khung này là (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38.
Chúng tôi sẽ sử dụng thuật toán của Prim để tìm cây bao trùm tối thiểu.
Thuật toán của Prim
Thuật toán của Prim là một cách tiếp cận tham lam để tìm cây bao trùm tối thiểu. Trong thuật toán này, để tạo MST, chúng ta có thể bắt đầu từ một đỉnh tùy ý.
Algorithm: MST-Prim’s (G, w, r)
for each u є G.V
u.key = ∞
u.∏ = NIL
r.key = 0
Q = G.V
while Q ≠ Ф
u = Extract-Min (Q)
for each v є G.adj[u]
if each v є Q and w(u, v) < v.key
v.∏ = u
v.key = w(u, v)Hàm Extract-Min trả về đỉnh có chi phí cạnh tối thiểu. Chức năng này hoạt động trên min-heap.
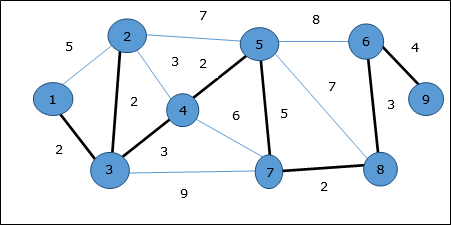
Thí dụ
Sử dụng thuật toán Prim, chúng ta có thể bắt đầu từ bất kỳ đỉnh nào, hãy bắt đầu từ đỉnh 1.
Đỉnh 3 được kết nối với đỉnh 1 với chi phí cạnh tối thiểu, do đó cạnh (1, 2) được thêm vào cây khung.
Tiếp theo, cạnh (2, 3) được coi là mức tối thiểu trong số các cạnh {(1, 2), (2, 3), (3, 4), (3, 7)}.
Trong bước tiếp theo, chúng ta có được lợi thế (3, 4) và (2, 4)với chi phí tối thiểu. Cạnh(3, 4) được chọn ngẫu nhiên.
Theo một cách tương tự, các cạnh (4, 5), (5, 7), (7, 8), (6, 8) và (6, 9)được chọn. Khi tất cả các đỉnh được thăm, bây giờ thuật toán dừng lại.
Chi phí của cây bao trùm là (2 + 2 + 3 + 2 + 5 + 2 + 3 + 4) = 23. Không có cây bao trùm nào trong đồ thị này với chi phí nhỏ hơn 23.
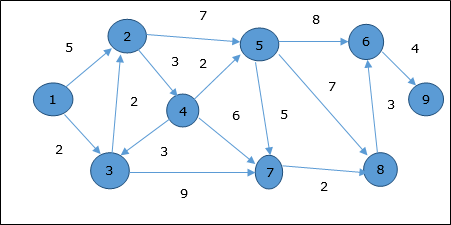
Thuật toán Dijkstra
Thuật toán Dijkstra giải quyết vấn đề đường đi ngắn nhất nguồn đơn trên đồ thị có trọng số có hướng G = (V, E) , trong đó tất cả các cạnh đều không âm (tức là, w (u, v) ≥ 0 đối với mỗi cạnh (u, v ) Є E ).
Trong thuật toán sau, chúng ta sẽ sử dụng một hàm Extract-Min(), sẽ trích xuất nút có khóa nhỏ nhất.
Algorithm: Dijkstra’s-Algorithm (G, w, s)
for each vertex v Є G.V
v.d := ∞
v.∏ := NIL
s.d := 0
S := Ф
Q := G.V
while Q ≠ Ф
u := Extract-Min (Q)
S := S U {u}
for each vertex v Є G.adj[u]
if v.d > u.d + w(u, v)
v.d := u.d + w(u, v)
v.∏ := uPhân tích
Độ phức tạp của thuật toán này hoàn toàn phụ thuộc vào việc thực hiện hàm Extract-Min. Nếu hàm min trích xuất được thực hiện bằng cách sử dụng tìm kiếm tuyến tính, thì độ phức tạp của thuật toán này làO(V2 + E).
Trong thuật toán này, nếu chúng ta sử dụng min-heap trên đó Extract-Min() hàm hoạt động để trả về nút từ Q với khóa nhỏ nhất, độ phức tạp của thuật toán này có thể được giảm thêm.
Thí dụ
Hãy để chúng tôi xem xét đỉnh 1 và 9là đỉnh xuất phát và đích tương ứng. Ban đầu, tất cả các đỉnh ngoại trừ đỉnh bắt đầu được đánh dấu bằng ∞ và đỉnh bắt đầu được đánh dấu bằng0.
| Đỉnh | Ban đầu | Bước 1 V 1 | Bước 2 V 3 | Bước 3 V 2 | Bước 4 V 4 | Bước 5 V 5 | Bước 6 V 7 | Bước 7 V 8 | Bước 8 V 6 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | ∞ | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 3 | ∞ | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 4 | ∞ | ∞ | ∞ | 7 | 7 | 7 | 7 | 7 | 7 |
| 5 | ∞ | ∞ | ∞ | 11 | 9 | 9 | 9 | 9 | 9 |
| 6 | ∞ | ∞ | ∞ | ∞ | ∞ | 17 | 17 | 16 | 16 |
| 7 | ∞ | ∞ | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| số 8 | ∞ | ∞ | ∞ | ∞ | ∞ | 16 | 13 | 13 | 13 |
| 9 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 20 |
Do đó, khoảng cách tối thiểu của đỉnh 9 từ đỉnh 1 Là 20. Và con đường là
1 → 3 → 7 → 8 → 6 → 9
Đường dẫn này được xác định dựa trên thông tin tiền nhiệm.
Thuật toán Bellman Ford
Thuật toán này giải quyết vấn đề đường đi ngắn nhất nguồn duy nhất của đồ thị có hướng G = (V, E)trong đó trọng số các cạnh có thể âm. Hơn nữa, thuật toán này có thể được áp dụng để tìm đường đi ngắn nhất, nếu không tồn tại bất kỳ chu trình có trọng số âm nào.
Algorithm: Bellman-Ford-Algorithm (G, w, s)
for each vertex v Є G.V
v.d := ∞
v.∏ := NIL
s.d := 0
for i = 1 to |G.V| - 1
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
v.d := u.d +w(u, v)
v.∏ := u
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
return FALSE
return TRUEPhân tích
Đầu tiên for vòng lặp được sử dụng để khởi tạo, chạy trong O(V)lần. Tiếp theofor vòng lặp chạy |V - 1| vượt qua các cạnh, mấtO(E) lần.
Do đó, thuật toán Bellman-Ford chạy trong O(V, E) thời gian.
Thí dụ
Ví dụ sau đây cho thấy cách thức hoạt động của thuật toán Bellman-Ford từng bước. Đồ thị này có một cạnh âm nhưng không có bất kỳ chu trình âm nào, do đó vấn đề có thể được giải quyết bằng cách sử dụng kỹ thuật này.
Tại thời điểm khởi tạo, tất cả các đỉnh ngoại trừ nguồn được đánh dấu bằng ∞ và nguồn được đánh dấu bằng 0.
Trong bước đầu tiên, tất cả các đỉnh có thể truy cập từ nguồn được cập nhật bằng chi phí tối thiểu. Do đó, các đỉnha và h được cập nhật.
Trong bước tiếp theo, các đỉnh a, b, f và e được cập nhật.
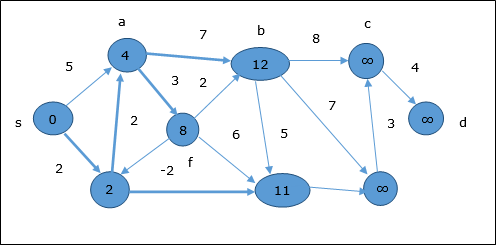
Theo cùng một logic, trong bước này các đỉnh b, f, c và g được cập nhật.
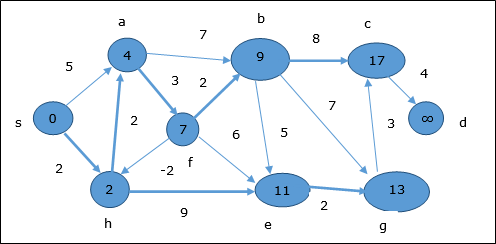
Đây, các đỉnh c và d được cập nhật.
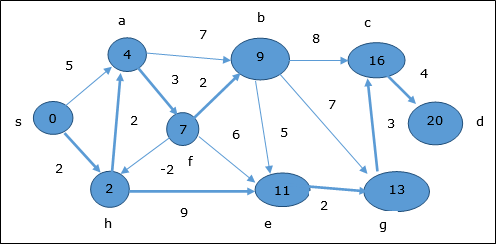
Do đó, khoảng cách tối thiểu giữa các đỉnh s và đỉnh d Là 20.
Dựa trên thông tin tiền nhiệm, con đường là s → h → e → g → c → d
Biểu đồ nhiều tầng G = (V, E) là một đồ thị có hướng trong đó các đỉnh được phân chia thành k (Ở đâu k > 1) số lượng các tập con rời rạc S = {s1,s2,…,sk}sao cho cạnh (u, v) nằm trong E, thì u Є s i và v Є s 1 + 1 cho một số tập con trong phân hoạch và |s1| = |sk| = 1.
Đỉnh s Є s1 nó được gọi là source và đỉnh t Є sk được gọi là sink.
Gthường được giả định là một đồ thị có trọng số. Trong đồ thị này, chi phí của một cạnh (i, j) được biểu thị bằng c (i, j) . Do đó, chi phí của đường dẫn từ nguồns để chìm t là tổng chi phí của mỗi cạnh trong đường dẫn này.
Bài toán biểu đồ nhiều tầng là tìm đường dẫn với chi phí tối thiểu từ nguồn s để chìm t.
Thí dụ
Hãy xem xét ví dụ sau để hiểu khái niệm về đồ thị nhiều tầng.
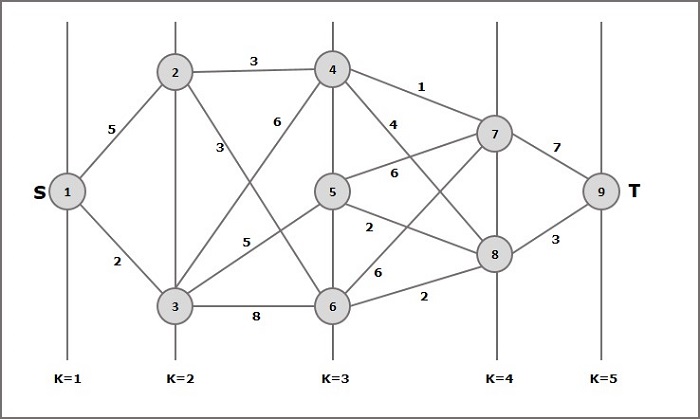
Theo công thức, chúng ta phải tính toán chi phí (i, j) sử dụng các bước sau
Bước-1: Chi phí (K-2, j)
Trong bước này, ba nút (nút 4, 5, 5) được chọn là j. Do đó, chúng tôi có ba tùy chọn để chọn chi phí tối thiểu ở bước này.
Chi phí (3, 4) = tối thiểu {c (4, 7) + Chi phí (7, 9), c (4, 8) + Chi phí (8, 9)} = 7
Chi phí (3, 5) = min {c (5, 7) + Cost (7, 9), c (5, 8) + Cost (8, 9)} = 5
Chi phí (3, 6) = tối thiểu {c (6, 7) + Chi phí (7, 9), c (6, 8) + Chi phí (8, 9)} = 5
Bước 2: Chi phí (K-3, j)
Hai nút được chọn là j vì ở giai đoạn k - 3 = 2 có hai nút là 2 và 3. Vì vậy, giá trị i = 2 và j = 2 và 3.
Chi phí (2, 2) = min {c (2, 4) + Cost (4, 8) + Cost (8, 9), c (2, 6) +
Chi phí (6, 8) + Chi phí (8, 9)} = 8
Chi phí (2, 3) = {c (3, 4) + Chi phí (4, 8) + Chi phí (8, 9), c (3, 5) + Chi phí (5, 8) + Chi phí (8, 9), c (3, 6) + Chi phí (6, 8) + Chi phí (8, 9)} = 10
Bước-3: Chi phí (K-4, j)
Chi phí (1, 1) = {c (1, 2) + Chi phí (2, 6) + Chi phí (6, 8) + Chi phí (8, 9), c (1, 3) + Chi phí (3, 5) + Chi phí (5, 8) + Chi phí (8, 9))} = 12
c (1, 3) + Chi phí (3, 6) + Chi phí (6, 8 + Chi phí (8, 9))} = 13
Do đó, con đường có chi phí tối thiểu là 1→ 3→ 5→ 8→ 9.
Báo cáo vấn đề
Một khách du lịch cần đến thăm tất cả các thành phố từ một danh sách, trong đó khoảng cách giữa tất cả các thành phố được biết đến và mỗi thành phố chỉ nên đến thăm một lần. Con đường ngắn nhất có thể mà anh ta đến thăm mỗi thành phố đúng một lần và quay trở lại thành phố gốc là gì?
Giải pháp
Bài toán nhân viên bán hàng đi du lịch là bài toán tính toán khét tiếng nhất. Chúng tôi có thể sử dụng phương pháp tiếp cận bạo lực để đánh giá mọi chuyến tham quan có thể có và chọn chuyến tham quan tốt nhất. Đối vớin số đỉnh trong một đồ thị, có (n - 1)! số khả năng.
Thay vì sử dụng cách tiếp cận lập trình động, giải pháp có thể đạt được trong thời gian ngắn hơn, mặc dù không có thuật toán thời gian đa thức.
Hãy để chúng tôi xem xét một biểu đồ G = (V, E), Ở đâu V là một tập hợp các thành phố và Elà tập hợp các cạnh có trọng số. Một cạnhe(u, v) đại diện cho các đỉnh đó u và vđược kết nối. Khoảng cách giữa các đỉnhu và v Là d(u, v), không được âm.
Giả sử chúng ta đã bắt đầu ở thành phố 1 và sau khi thăm một số thành phố, bây giờ chúng tôi ở thành phố j. Do đó, đây là một chuyến tham quan một phần. Chúng tôi chắc chắn cần biếtj, vì điều này sẽ xác định thành phố nào thuận tiện nhất để ghé thăm tiếp theo. Chúng tôi cũng cần biết tất cả các thành phố đã ghé thăm cho đến nay, để chúng tôi không lặp lại bất kỳ thành phố nào. Do đó, đây là một vấn đề phụ thích hợp.
Đối với một tập hợp con các thành phố S Є {1, 2, 3, ... , n} bao gồm 1và j Є S, để cho C(S, j) là độ dài của đường đi ngắn nhất truy cập vào mỗi nút trong S chính xác một lần, bắt đầu từ 1 và kết thúc ở j.
Khi nào |S| > 1, chúng tôi xác địnhC(S, 1) = ∝ vì đường dẫn không thể bắt đầu và kết thúc tại 1.
Bây giờ, hãy bày tỏ C(S, j)xét về các vấn đề phụ nhỏ hơn. Chúng ta cần bắt đầu lúc1 và kết thúc ở j. Chúng ta nên chọn thành phố tiếp theo theo cách
$$C(S, j) = min \:C(S - \lbrace j \rbrace, i) + d(i, j)\:where\: i\in S \: and\: i \neq jc(S, j) = minC(s- \lbrace j \rbrace, i)+ d(i,j) \:where\: i\in S \: and\: i \neq j $$
Algorithm: Traveling-Salesman-Problem
C ({1}, 1) = 0
for s = 2 to n do
for all subsets S Є {1, 2, 3, … , n} of size s and containing 1
C (S, 1) = ∞
for all j Є S and j ≠ 1
C (S, j) = min {C (S – {j}, i) + d(i, j) for i Є S and i ≠ j}
Return minj C ({1, 2, 3, …, n}, j) + d(j, i)Phân tích
Có nhiều nhất $2^n.n$các bài toán con và mỗi bài toán cần thời gian tuyến tính để giải. Do đó, tổng thời gian chạy là$O(2^n.n^2)$.
Thí dụ
Trong ví dụ sau, chúng tôi sẽ minh họa các bước để giải quyết vấn đề nhân viên bán hàng đi du lịch.

Từ đồ thị trên, lập bảng sau.
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 10 | 15 | 20 |
| 2 | 5 | 0 | 9 | 10 |
| 3 | 6 | 13 | 0 | 12 |
| 4 | số 8 | số 8 | 9 | 0 |
S = Φ
$$\small Cost (2,\Phi,1) = d (2,1) = 5\small Cost(2,\Phi,1)=d(2,1)=5$$
$$\small Cost (3,\Phi,1) = d (3,1) = 6\small Cost(3,\Phi,1)=d(3,1)=6$$
$$\small Cost (4,\Phi,1) = d (4,1) = 8\small Cost(4,\Phi,1)=d(4,1)=8$$
S = 1
$$\small Cost (i,s) = min \lbrace Cost (j,s – (j)) + d [i,j]\rbrace\small Cost (i,s)=min \lbrace Cost (j,s)-(j))+ d [i,j]\rbrace$$
$$\small Cost (2,\lbrace 3 \rbrace,1) = d [2,3] + Cost (3,\Phi,1) = 9 + 6 = 15cost(2,\lbrace3 \rbrace,1)=d[2,3]+cost(3,\Phi ,1)=9+6=15$$
$$\small Cost (2,\lbrace 4 \rbrace,1) = d [2,4] + Cost (4,\Phi,1) = 10 + 8 = 18cost(2,\lbrace4 \rbrace,1)=d[2,4]+cost(4,\Phi,1)=10+8=18$$
$$\small Cost (3,\lbrace 2 \rbrace,1) = d [3,2] + Cost (2,\Phi,1) = 13 + 5 = 18cost(3,\lbrace2 \rbrace,1)=d[3,2]+cost(2,\Phi,1)=13+5=18$$
$$\small Cost (3,\lbrace 4 \rbrace,1) = d [3,4] + Cost (4,\Phi,1) = 12 + 8 = 20cost(3,\lbrace4 \rbrace,1)=d[3,4]+cost(4,\Phi,1)=12+8=20$$
$$\small Cost (4,\lbrace 3 \rbrace,1) = d [4,3] + Cost (3,\Phi,1) = 9 + 6 = 15cost(4,\lbrace3 \rbrace,1)=d[4,3]+cost(3,\Phi,1)=9+6=15$$
$$\small Cost (4,\lbrace 2 \rbrace,1) = d [4,2] + Cost (2,\Phi,1) = 8 + 5 = 13cost(4,\lbrace2 \rbrace,1)=d[4,2]+cost(2,\Phi,1)=8+5=13$$
S = 2
$$\small Cost(2, \lbrace 3, 4 \rbrace, 1)=\begin{cases}d[2, 3] + Cost(3, \lbrace 4 \rbrace, 1) = 9 + 20 = 29\\d[2, 4] + Cost(4, \lbrace 3 \rbrace, 1) = 10 + 15 = 25=25\small Cost (2,\lbrace 3,4 \rbrace,1)\\\lbrace d[2,3]+ \small cost(3,\lbrace4\rbrace,1)=9+20=29d[2,4]+ \small Cost (4,\lbrace 3 \rbrace ,1)=10+15=25\end{cases}= 25$$
$$\small Cost(3, \lbrace 2, 4 \rbrace, 1)=\begin{cases}d[3, 2] + Cost(2, \lbrace 4 \rbrace, 1) = 13 + 18 = 31\\d[3, 4] + Cost(4, \lbrace 2 \rbrace, 1) = 12 + 13 = 25=25\small Cost (3,\lbrace 2,4 \rbrace,1)\\\lbrace d[3,2]+ \small cost(2,\lbrace4\rbrace,1)=13+18=31d[3,4]+ \small Cost (4,\lbrace 2 \rbrace ,1)=12+13=25\end{cases}= 25$$
$$\small Cost(4, \lbrace 2, 3 \rbrace, 1)=\begin{cases}d[4, 2] + Cost(2, \lbrace 3 \rbrace, 1) = 8 + 15 = 23\\d[4, 3] + Cost(3, \lbrace 2 \rbrace, 1) = 9 + 18 = 27=23\small Cost (4,\lbrace 2,3 \rbrace,1)\\\lbrace d[4,2]+ \small cost(2,\lbrace3\rbrace,1)=8+15=23d[4,3]+ \small Cost (3,\lbrace 2 \rbrace ,1)=9+18=27\end{cases}= 23$$
S = 3
$$\small Cost(1, \lbrace 2, 3, 4 \rbrace, 1)=\begin{cases}d[1, 2] + Cost(2, \lbrace 3, 4 \rbrace, 1) = 10 + 25 = 35\\d[1, 3] + Cost(3, \lbrace 2, 4 \rbrace, 1) = 15 + 25 = 40\\d[1, 4] + Cost(4, \lbrace 2, 3 \rbrace, 1) = 20 + 23 = 43=35 cost(1,\lbrace 2,3,4 \rbrace),1)\\d[1,2]+cost(2,\lbrace 3,4 \rbrace,1)=10+25=35\\d[1,3]+cost(3,\lbrace 2,4 \rbrace,1)=15+25=40\\d[1,4]+cost(4,\lbrace 2,3 \rbrace ,1)=20+23=43=35\end{cases}$$
Đường dẫn chi phí tối thiểu là 35.
Bắt đầu từ chi phí {1, {2, 3, 4}, 1}, chúng tôi nhận được giá trị tối thiểu cho d [1, 2]. Khi nàos = 3, chọn đường dẫn từ 1 đến 2 (chi phí là 10) sau đó quay ngược lại. Khi nàos = 2, chúng tôi nhận được giá trị tối thiểu cho d [4, 2]. Chọn con đường từ 2 đến 4 (chi phí là 10) sau đó đi ngược lại.
Khi nào s = 1, chúng tôi nhận được giá trị tối thiểu cho d [4, 3]. Chọn đường dẫn 4 đến 3 (chi phí là 9), sau đó chúng ta sẽ đi đếns = Φbươc. Chúng tôi nhận được giá trị tối thiểu chod [3, 1] (chi phí là 6).

Cây tìm kiếm nhị phân (BST) là cây nơi các giá trị khóa được lưu trữ trong các nút bên trong. Các nút bên ngoài là các nút rỗng. Các khóa được sắp xếp theo thứ tự từ vựng, nghĩa là đối với mỗi nút bên trong, tất cả các khóa trong cây con bên trái nhỏ hơn các khóa trong nút và tất cả các khóa trong cây con bên phải lớn hơn.
Khi chúng ta biết tần suất tìm kiếm từng khóa, sẽ khá dễ dàng để tính toán chi phí dự kiến của việc truy cập từng nút trong cây. Cây tìm kiếm nhị phân tối ưu là một BST có chi phí định vị mỗi nút dự kiến tối thiểu
Thời gian tìm kiếm của một phần tử trong BST là O(n), trong khi thời gian tìm kiếm theo BST Balanced là O(log n). Một lần nữa, thời gian tìm kiếm có thể được cải thiện trong Cây Tìm kiếm Nhị phân Chi phí Tối ưu, đặt dữ liệu được sử dụng thường xuyên nhất trong phần tử gốc và gần phần tử gốc hơn, trong khi đặt dữ liệu ít được sử dụng nhất gần các lá và trong các lá.
Ở đây, thuật toán cây tìm kiếm nhị phân tối ưu được trình bày. Đầu tiên, chúng tôi xây dựng một BST từ một tập hợp cácn số lượng khóa riêng biệt < k1, k2, k3, ... kn >. Ở đây chúng tôi giả định, xác suất truy cập một khóaKi Là pi. Một số phím giả (d0, d1, d2, ... dn) được thêm vào vì một số tìm kiếm có thể được thực hiện cho các giá trị không có trong Bộ khóa K. Chúng tôi giả định, đối với mỗi khóa giảdi xác suất truy cập là qi.
Optimal-Binary-Search-Tree(p, q, n)
e[1…n + 1, 0…n],
w[1…n + 1, 0…n],
root[1…n + 1, 0…n]
for i = 1 to n + 1 do
e[i, i - 1] := qi - 1
w[i, i - 1] := qi - 1
for l = 1 to n do
for i = 1 to n – l + 1 do
j = i + l – 1 e[i, j] := ∞
w[i, i] := w[i, i -1] + pj + qj
for r = i to j do
t := e[i, r - 1] + e[r + 1, j] + w[i, j]
if t < e[i, j]
e[i, j] := t
root[i, j] := r
return e and rootPhân tích
Thuật toán yêu cầu O (n3) thời gian, kể từ khi ba lồng vào nhau forvòng lặp được sử dụng. Mỗi vòng lặp này đảm nhiệm tối đan các giá trị.
Thí dụ
Xem xét cây sau, chi phí là 2,80, mặc dù đây không phải là kết quả tối ưu.
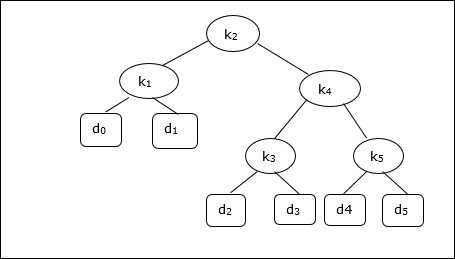
| Nút | Chiều sâu | Xác suất | Sự đóng góp |
|---|---|---|---|
| k 1 | 1 | 0,15 | 0,30 |
| k 2 | 0 | 0,10 | 0,10 |
| k 3 | 2 | 0,05 | 0,15 |
| k 4 | 1 | 0,10 | 0,20 |
| k 5 | 2 | 0,20 | 0,60 |
| d 0 | 2 | 0,05 | 0,15 |
| d 1 | 2 | 0,10 | 0,30 |
| d 2 | 3 | 0,05 | 0,20 |
| d 3 | 3 | 0,05 | 0,20 |
| d 4 | 3 | 0,05 | 0,20 |
| d 5 | 3 | 0,10 | 0,40 |
| Total | 2,80 |
Để có được một giải pháp tối ưu, sử dụng thuật toán được thảo luận trong chương này, các bảng sau được tạo.
Trong các bảng sau, chỉ mục cột là i và chỉ số hàng là j.
| e | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 5 | 2,75 | 2,00 | 1,30 | 0,90 | 0,50 | 0,10 |
| 4 | 1,75 | 1,20 | 0,60 | 0,30 | 0,05 | |
| 3 | 1,25 | 0,70 | 0,25 | 0,05 | ||
| 2 | 0,90 | 0,40 | 0,05 | |||
| 1 | 0,45 | 0,10 | ||||
| 0 | 0,05 |
| w | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 5 | 1,00 | 0,80 | 0,60 | 0,50 | 0,35 | 0,10 |
| 4 | 0,70 | 0,50 | 0,30 | 0,20 | 0,05 | |
| 3 | 0,55 | 0,35 | 0,15 | 0,05 | ||
| 2 | 0,45 | 0,25 | 0,05 | |||
| 1 | 0,30 | 0,10 | ||||
| 0 | 0,05 |
| nguồn gốc | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 5 | 2 | 4 | 5 | 5 | 5 |
| 4 | 2 | 2 | 4 | 4 | |
| 3 | 2 | 2 | 3 | ||
| 2 | 1 | 2 | |||
| 1 | 1 |
From these tables, the optimal tree can be formed.
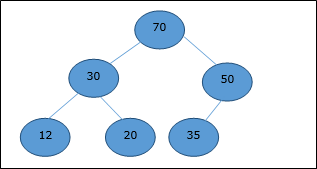
There are several types of heaps, however in this chapter, we are going to discuss binary heap. A binary heap is a data structure, which looks similar to a complete binary tree. Heap data structure obeys ordering properties discussed below. Generally, a Heap is represented by an array. In this chapter, we are representing a heap by H.
As the elements of a heap is stored in an array, considering the starting index as 1, the position of the parent node of ith element can be found at ⌊ i/2 ⌋ . Left child and right child of ith node is at position 2i and 2i + 1.
A binary heap can be classified further as either a max-heap or a min-heap based on the ordering property.
Max-Heap
In this heap, the key value of a node is greater than or equal to the key value of the highest child.
Hence, H[Parent(i)] ≥ H[i]
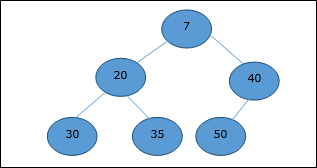
Min-Heap
In mean-heap, the key value of a node is lesser than or equal to the key value of the lowest child.
Hence, H[Parent(i)] ≤ H[i]
In this context, basic operations are shown below with respect to Max-Heap. Insertion and deletion of elements in and from heaps need rearrangement of elements. Hence, Heapify function needs to be called.
Array Representation
A complete binary tree can be represented by an array, storing its elements using level order traversal.
Let us consider a heap (as shown below) which will be represented by an array H.
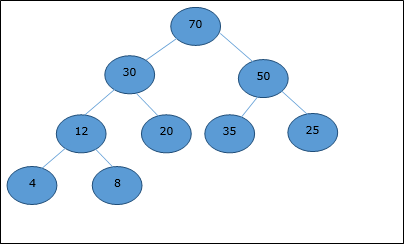
Considering the starting index as 0, using level order traversal, the elements are being kept in an array as follows.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| elements | 70 | 30 | 50 | 12 | 20 | 35 | 25 | 4 | 8 | ... |
In this context, operations on heap are being represented with respect to Max-Heap.
To find the index of the parent of an element at index i, the following algorithm Parent (numbers[], i) is used.
Algorithm: Parent (numbers[], i)
if i == 1
return NULL
else
[i / 2]The index of the left child of an element at index i can be found using the following algorithm, Left-Child (numbers[], i).
Algorithm: Left-Child (numbers[], i)
If 2 * i ≤ heapsize
return [2 * i]
else
return NULLThe index of the right child of an element at index i can be found using the following algorithm, Right-Child(numbers[], i).
Algorithm: Right-Child (numbers[], i)
if 2 * i < heapsize
return [2 * i + 1]
else
return NULLTo insert an element in a heap, the new element is initially appended to the end of the heap as the last element of the array.
After inserting this element, heap property may be violated, hence the heap property is repaired by comparing the added element with its parent and moving the added element up a level, swapping positions with the parent. This process is called percolation up.
The comparison is repeated until the parent is larger than or equal to the percolating element.
Algorithm: Max-Heap-Insert (numbers[], key)
heapsize = heapsize + 1
numbers[heapsize] = -∞
i = heapsize
numbers[i] = key
while i > 1 and numbers[Parent(numbers[], i)] < numbers[i]
exchange(numbers[i], numbers[Parent(numbers[], i)])
i = Parent (numbers[], i)Analysis
Initially, an element is being added at the end of the array. If it violates the heap property, the element is exchanged with its parent. The height of the tree is log n. Maximum log n number of operations needs to be performed.
Hence, the complexity of this function is O(log n).
Example
Let us consider a max-heap, as shown below, where a new element 5 needs to be added.
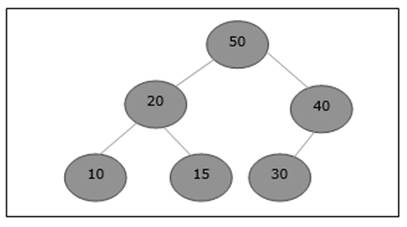
Initially, 55 will be added at the end of this array.
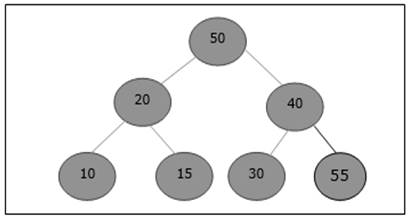
After insertion, it violates the heap property. Hence, the element needs to swap with its parent. After swap, the heap looks like the following.
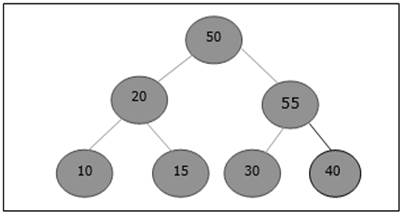
Again, the element violates the property of heap. Hence, it is swapped with its parent.
Now, we have to stop.
Heapify method rearranges the elements of an array where the left and right sub-tree of ith element obeys the heap property.
Algorithm: Max-Heapify(numbers[], i)
leftchild := numbers[2i]
rightchild := numbers [2i + 1]
if leftchild ≤ numbers[].size and numbers[leftchild] > numbers[i]
largest := leftchild
else
largest := i
if rightchild ≤ numbers[].size and numbers[rightchild] > numbers[largest]
largest := rightchild
if largest ≠ i
swap numbers[i] with numbers[largest]
Max-Heapify(numbers, largest)When the provided array does not obey the heap property, Heap is built based on the following algorithm Build-Max-Heap (numbers[]).
Algorithm: Build-Max-Heap(numbers[])
numbers[].size := numbers[].length
fori = ⌊ numbers[].length/2 ⌋ to 1 by -1
Max-Heapify (numbers[], i)Extract method is used to extract the root element of a Heap. Following is the algorithm.
Algorithm: Heap-Extract-Max (numbers[])
max = numbers[1]
numbers[1] = numbers[heapsize]
heapsize = heapsize – 1
Max-Heapify (numbers[], 1)
return maxExample
Let us consider the same example discussed previously. Now we want to extract an element. This method will return the root element of the heap.
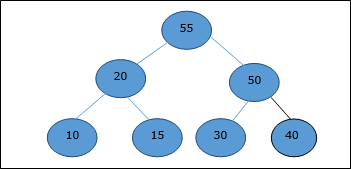
After deletion of the root element, the last element will be moved to the root position.
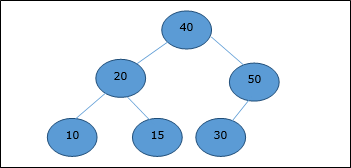
Now, Heapify function will be called. After Heapify, the following heap is generated.
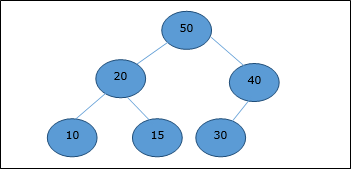
Bubble Sort is an elementary sorting algorithm, which works by repeatedly exchanging adjacent elements, if necessary. When no exchanges are required, the file is sorted.
This is the simplest technique among all sorting algorithms.
Algorithm: Sequential-Bubble-Sort (A)
fori← 1 to length [A] do
for j ← length [A] down-to i +1 do
if A[A] < A[j - 1] then
Exchange A[j] ↔ A[j-1]Implementation
voidbubbleSort(int numbers[], intarray_size) {
inti, j, temp;
for (i = (array_size - 1); i >= 0; i--)
for (j = 1; j <= i; j++)
if (numbers[j - 1] > numbers[j]) {
temp = numbers[j-1];
numbers[j - 1] = numbers[j];
numbers[j] = temp;
}
}Analysis
Here, the number of comparisons are
1 + 2 + 3 +...+ (n - 1) = n(n - 1)/2 = O(n2)
Clearly, the graph shows the n2 nature of the bubble sort.
In this algorithm, the number of comparison is irrespective of the data set, i.e. whether the provided input elements are in sorted order or in reverse order or at random.
Memory Requirement
From the algorithm stated above, it is clear that bubble sort does not require extra memory.
Example
Unsorted list: |
|
1st iteration:
5 > 2 swap |
|
|||||||
5 > 1 swap |
|
|||||||
5 > 4 swap |
|
|||||||
5 > 3 swap |
|
|||||||
5 < 7 no swap |
|
|||||||
7 > 6 swap |
|
2nd iteration:
2 > 1 swap |
|
|||||||
2 < 4 no swap |
|
|||||||
4 > 3 swap |
|
|||||||
4 < 5 no swap |
|
|||||||
5 < 6 no swap |
|
There is no change in 3rd, 4th, 5th and 6th iteration.
Finally,
the sorted list is |
|
Insertion sort is a very simple method to sort numbers in an ascending or descending order. This method follows the incremental method. It can be compared with the technique how cards are sorted at the time of playing a game.
The numbers, which are needed to be sorted, are known as keys. Here is the algorithm of the insertion sort method.
Algorithm: Insertion-Sort(A)
for j = 2 to A.length
key = A[j]
i = j – 1
while i > 0 and A[i] > key
A[i + 1] = A[i]
i = i -1
A[i + 1] = keyAnalysis
Run time of this algorithm is very much dependent on the given input.
If the given numbers are sorted, this algorithm runs in O(n) time. If the given numbers are in reverse order, the algorithm runs in O(n2) time.
Example
Unsorted list: |
|
1st iteration:
Key = a[2] = 13
a[1] = 2 < 13
Swap, no swap |
|
2nd iteration:
Key = a[3] = 5
a[2] = 13 > 5
Swap 5 and 13 |
|
Next, a[1] = 2 < 13
Swap, no swap |
|
3rd iteration:
Key = a[4] = 18
a[3] = 13 < 18,
a[2] = 5 < 18,
a[1] = 2 < 18
Swap, no swap |
|
4th iteration:
Key = a[5] = 14
a[4] = 18 > 14
Swap 18 and 14 |
|
Next, a[3] = 13 < 14,
a[2] = 5 < 14,
a[1] = 2 < 14
So, no swap |
|
Finally,
the sorted list is |
|
This type of sorting is called Selection Sort as it works by repeatedly sorting elements. It works as follows: first find the smallest in the array and exchange it with the element in the first position, then find the second smallest element and exchange it with the element in the second position, and continue in this way until the entire array is sorted.
Algorithm: Selection-Sort (A)
fori ← 1 to n-1 do
min j ← i;
min x ← A[i]
for j ←i + 1 to n do
if A[j] < min x then
min j ← j
min x ← A[j]
A[min j] ← A [i]
A[i] ← min xSelection sort is among the simplest of sorting techniques and it works very well for small files. It has a quite important application as each item is actually moved at the most once.
Section sort is a method of choice for sorting files with very large objects (records) and small keys. The worst case occurs if the array is already sorted in a descending order and we want to sort them in an ascending order.
Nonetheless, the time required by selection sort algorithm is not very sensitive to the original order of the array to be sorted: the test if A[j] < min x is executed exactly the same number of times in every case.
Selection sort spends most of its time trying to find the minimum element in the unsorted part of the array. It clearly shows the similarity between Selection sort and Bubble sort.
Bubble sort selects the maximum remaining elements at each stage, but wastes some effort imparting some order to an unsorted part of the array.
Selection sort is quadratic in both the worst and the average case, and requires no extra memory.
For each i from 1 to n - 1, there is one exchange and n - i comparisons, so there is a total of n - 1 exchanges and
(n − 1) + (n − 2) + ...+ 2 + 1 = n(n − 1)/2 comparisons.
These observations hold, no matter what the input data is.
In the worst case, this could be quadratic, but in the average case, this quantity is O(n log n). It implies that the running time of Selection sort is quite insensitive to the input.
Implementation
Void Selection-Sort(int numbers[], int array_size) {
int i, j;
int min, temp;
for (i = 0; I < array_size-1; i++) {
min = i;
for (j = i+1; j < array_size; j++)
if (numbers[j] < numbers[min])
min = j;
temp = numbers[i];
numbers[i] = numbers[min];
numbers[min] = temp;
}
}Example
Unsorted list: |
|
1st iteration:
Smallest = 5
2 < 5, smallest = 2
1 < 2, smallest = 1
4 > 1, smallest = 1
3 > 1, smallest = 1
Swap 5 and 1 |
|
2nd iteration:
Smallest = 2
2 < 5, smallest = 2
2 < 4, smallest = 2
2 < 3, smallest = 2
No Swap |
|
3rd iteration:
Smallest = 5
4 < 5, smallest = 4
3 < 4, smallest = 3
Swap 5 and 3 |
|
4th iteration:
Smallest = 4
4 < 5, smallest = 4
No Swap |
|
Finally,
the sorted list is |
|
It is used on the principle of divide-and-conquer. Quick sort is an algorithm of choice in many situations as it is not difficult to implement. It is a good general purpose sort and it consumes relatively fewer resources during execution.
Advantages
It is in-place since it uses only a small auxiliary stack.
It requires only n (log n) time to sort n items.
It has an extremely short inner loop.
This algorithm has been subjected to a thorough mathematical analysis, a very precise statement can be made about performance issues.
Disadvantages
It is recursive. Especially, if recursion is not available, the implementation is extremely complicated.
It requires quadratic (i.e., n2) time in the worst-case.
It is fragile, i.e. a simple mistake in the implementation can go unnoticed and cause it to perform badly.
Quick sort works by partitioning a given array A[p ... r] into two non-empty sub array A[p ... q] and A[q+1 ... r] such that every key in A[p ... q] is less than or equal to every key in A[q+1 ... r].
Then, the two sub-arrays are sorted by recursive calls to Quick sort. The exact position of the partition depends on the given array and index q is computed as a part of the partitioning procedure.
Algorithm: Quick-Sort (A, p, r)
if p < r then
q Partition (A, p, r)
Quick-Sort (A, p, q)
Quick-Sort (A, q + r, r)Note that to sort the entire array, the initial call should be Quick-Sort (A, 1, length[A])
As a first step, Quick Sort chooses one of the items in the array to be sorted as pivot. Then, the array is partitioned on either side of the pivot. Elements that are less than or equal to pivot will move towards the left, while the elements that are greater than or equal to pivot will move towards the right.
Partitioning the Array
Partitioning procedure rearranges the sub-arrays in-place.
Function: Partition (A, p, r)
x ← A[p]
i ← p-1
j ← r+1
while TRUE do
Repeat j ← j - 1
until A[j] ≤ x
Repeat i← i+1
until A[i] ≥ x
if i < j then
exchange A[i] ↔ A[j]
else
return jAnalysis
The worst case complexity of Quick-Sort algorithm is O(n2). However using this technique, in average cases generally we get the output in O(n log n) time.
Radix sort is a small method that many people intuitively use when alphabetizing a large list of names. Specifically, the list of names is first sorted according to the first letter of each name, that is, the names are arranged in 26 classes.
Intuitively, one might want to sort numbers on their most significant digit. However, Radix sort works counter-intuitively by sorting on the least significant digits first. On the first pass, all the numbers are sorted on the least significant digit and combined in an array. Then on the second pass, the entire numbers are sorted again on the second least significant digits and combined in an array and so on.
Algorithm: Radix-Sort (list, n)
shift = 1
for loop = 1 to keysize do
for entry = 1 to n do
bucketnumber = (list[entry].key / shift) mod 10
append (bucket[bucketnumber], list[entry])
list = combinebuckets()
shift = shift * 10Phân tích
Mỗi phím được xem một lần cho mỗi chữ số (hoặc chữ cái nếu các phím là bảng chữ cái) của khóa dài nhất. Do đó, nếu khóa dài nhất cóm chữ số và có n phím, sắp xếp cơ số có thứ tự O(m.n).
Tuy nhiên, nếu chúng ta nhìn vào hai giá trị này, kích thước của các phím sẽ tương đối nhỏ khi so sánh với số lượng phím. Ví dụ, nếu chúng ta có khóa sáu chữ số, chúng ta có thể có một triệu bản ghi khác nhau.
Ở đây, chúng tôi thấy rằng kích thước của các khóa không đáng kể và thuật toán này có độ phức tạp tuyến tính O(n).
Thí dụ
Ví dụ sau đây cho thấy cách sắp xếp Radix hoạt động trên bảy số có 3 chữ số.
| Đầu vào | 1 lần vượt qua | 2 nd đèo | 3 thứ đèo |
|---|---|---|---|
| 329 | 720 | 720 | 329 |
| 457 | 355 | 329 | 355 |
| 657 | 436 | 436 | 436 |
| 839 | 457 | 839 | 457 |
| 436 | 657 | 355 | 657 |
| 720 | 329 | 457 | 720 |
| 355 | 839 | 657 | 839 |
Trong ví dụ trên, cột đầu tiên là đầu vào. Các cột còn lại hiển thị danh sách sau khi sắp xếp liên tiếp ở vị trí các chữ số ngày càng có nghĩa. Mã cho sắp xếp Radix giả định rằng mỗi phần tử trong một mảngA của n yếu tố có d chữ số, chữ số ở đâu 1 là chữ số bậc thấp nhất và d là chữ số bậc cao nhất.
Để hiểu lớp học P và NP, trước tiên chúng ta nên biết mô hình tính toán. Do đó, trong chương này chúng ta sẽ thảo luận về hai mô hình tính toán quan trọng.
Tính toán xác định và lớp P
Máy Turing xác định
Một trong những mô hình này là máy Turing một băng xác định. Máy này bao gồm một điều khiển trạng thái hữu hạn, một đầu đọc-ghi và một băng hai chiều với trình tự vô hạn.
Sau đây là sơ đồ của một máy Turing một băng xác định.
Chương trình cho máy Turing xác định chỉ định thông tin sau:
- Một tập hợp hữu hạn các ký hiệu băng (ký hiệu đầu vào và một ký hiệu trống)
- Một tập hợp hữu hạn các trạng thái
- Một chức năng chuyển tiếp
Trong phân tích thuật toán, nếu một bài toán có thể giải được trong thời gian đa thức bằng máy Turing một băng xác định, bài toán đó thuộc lớp P.
Tính toán không xác định và lớp NP
Máy Turing không xác định
Để giải quyết vấn đề tính toán, một mô hình khác là Máy điều chỉnh không xác định (NDTM). Cấu trúc của NDTM tương tự như DTM, tuy nhiên ở đây chúng ta có một mô-đun bổ sung được gọi là mô-đun đoán, được liên kết với một đầu chỉ ghi.
Sau đây là sơ đồ.
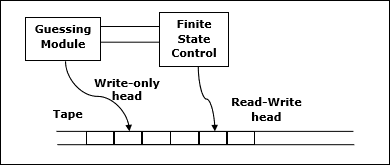
Nếu bài toán có thể giải được trong thời gian đa thức bằng máy Turing không xác định thì bài toán thuộc lớp NP.
Trong một biểu đồ vô hướng, một cliquelà một đồ thị con hoàn chỉnh của đồ thị đã cho. Đồ thị con hoàn chỉnh có nghĩa là, tất cả các đỉnh của đồ thị con này được nối với tất cả các đỉnh khác của đồ thị con này.
Bài toán Max-Clique là bài toán tính toán để tìm ra cực đại của đồ thị. Max clique được sử dụng trong nhiều bài toán trong thế giới thực.
Chúng ta hãy xem xét một ứng dụng mạng xã hội, trong đó các đỉnh đại diện cho hồ sơ của mọi người và các cạnh đại diện cho sự quen biết lẫn nhau trong một biểu đồ. Trong biểu đồ này, một nhóm đại diện cho một nhóm nhỏ những người đều biết nhau.
Để tìm một nhóm tối đa, người ta có thể kiểm tra một cách có hệ thống tất cả các tập con, nhưng kiểu tìm kiếm thô bạo này quá tốn thời gian đối với các mạng bao gồm hơn một vài chục đỉnh.
Algorithm: Max-Clique (G, n, k)
S := Φ
for i = 1 to k do
t := choice (1…n)
if t Є S then
return failure
S := S ∪ t
for all pairs (i, j) such that i Є S and j Є S and i ≠ j do
if (i, j) is not a edge of the graph then
return failure
return successPhân tích
Bài toán Max-Clique là một thuật toán không xác định. Trong thuật toán này, trước tiên chúng tôi cố gắng xác định một tập hợpk các đỉnh khác nhau và sau đó chúng tôi cố gắng kiểm tra xem các đỉnh này có tạo thành một đồ thị hoàn chỉnh hay không.
Không có thuật toán xác định thời gian đa thức để giải quyết vấn đề này. Vấn đề này là NP-Hoàn thành.
Thí dụ
Hãy nhìn vào đồ thị sau đây. Ở đây, đồ thị con chứa các đỉnh 2, 3, 4 và 6 tạo thành một đồ thị hoàn chỉnh. Do đó, biểu đồ phụ này là mộtclique. Vì đây là biểu đồ con hoàn chỉnh tối đa của biểu đồ được cung cấp, nên4-Clique.

Một đỉnh của đồ thị vô hướng G = (V, E) là một tập hợp con của các đỉnh V' ⊆ V như vậy nếu cạnh (u, v) là một cạnh của G, sau đó một trong hai u trong V hoặc là v trong V' hoặc cả hai.
Tìm một đỉnh có kích thước lớn nhất trong một đồ thị vô hướng đã cho. Lớp phủ đỉnh tối ưu này là phiên bản tối ưu hóa của một bài toán hoàn chỉnh NP. Tuy nhiên, không quá khó để tìm được một đỉnh gần như tối ưu.
APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G]
while E' is not empty do
Let (u, v) be an arbitrary edge of E' c ← c U {u, v}
Remove from E' every edge incident on either u or v
return cThí dụ
Tập hợp các cạnh của đồ thị đã cho là -
{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}
Bây giờ, chúng ta bắt đầu bằng cách chọn một cạnh tùy ý (1,6). Chúng tôi loại bỏ tất cả các cạnh, là sự cố đối với đỉnh 1 hoặc 6 và chúng tôi thêm cạnh (1,6) để che đi.
Trong bước tiếp theo, chúng tôi đã chọn một cạnh khác (2,3) một cách ngẫu nhiên
Bây giờ chúng ta chọn một cạnh khác (4,7).
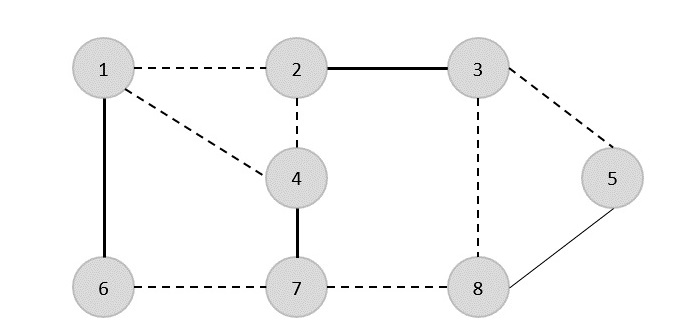
Chúng tôi chọn một cạnh khác (8,5).
Do đó, đỉnh của đồ thị này là {1,2,4,5}.
Phân tích
Dễ dàng nhận thấy rằng thời gian chạy của thuật toán này là O(V + E), sử dụng danh sách kề để đại diện E'.
Trong Khoa học Máy tính, nhiều vấn đề được giải quyết trong đó mục tiêu là tối đa hóa hoặc giảm thiểu một số giá trị, trong khi trong các vấn đề khác, chúng tôi cố gắng tìm ra giải pháp hay không. Do đó, các vấn đề có thể được phân loại như sau:
Vấn đề tối ưu hóa
Các vấn đề về tối ưu hóa là những vấn đề mà mục tiêu là tối đa hóa hoặc giảm thiểu một số giá trị. Ví dụ,
Tìm số màu tối thiểu cần thiết để tô màu một đồ thị đã cho.
Tìm đường đi ngắn nhất giữa hai đỉnh trong đồ thị.
Vấn đề quyết định
Có nhiều vấn đề mà câu trả lời là Có hoặc Không. Những loại vấn đề này được gọi là decision problems. Ví dụ,
Cho dù một biểu đồ nhất định chỉ có thể được tô màu bởi 4 màu.
Tìm chu trình Hamilton trong đồ thị không phải là vấn đề quyết định, ngược lại việc kiểm tra đồ thị có phải là Hamilton hay không là vấn đề quyết định.
Ngôn ngữ là gì?
Mọi vấn đề quyết định chỉ có thể có hai câu trả lời, có hoặc không. Do đó, một vấn đề quyết định có thể thuộc về một ngôn ngữ nếu nó cung cấp câu trả lời 'có' cho một đầu vào cụ thể. Một ngôn ngữ là tổng số đầu vào mà câu trả lời là Có. Hầu hết các thuật toán được thảo luận trong các chương trước làpolynomial time algorithms.
Đối với kích thước đầu vào n, nếu độ phức tạp thời gian trong trường hợp xấu nhất của một thuật toán là O(nk), Ở đâu k là một hằng số, thuật toán là một thuật toán thời gian đa thức.
Các thuật toán như Nhân chuỗi ma trận, Đường dẫn ngắn nhất nguồn đơn, Đường đi ngắn nhất theo cặp, Cây kéo dài tối thiểu, v.v. chạy trong thời gian đa thức. Tuy nhiên, có rất nhiều vấn đề, chẳng hạn như nhân viên bán hàng đi du lịch, tô màu đồ thị tối ưu, chu trình Hamilton, tìm đường đi dài nhất trong đồ thị và thỏa mãn công thức Boolean mà không có thuật toán thời gian đa thức nào được biết đến. Những vấn đề này thuộc về một loại vấn đề thú vị, được gọi làNP-Complete vấn đề mà trạng thái không xác định.
Trong bối cảnh này, chúng ta có thể phân loại các vấn đề như sau:
P-Class
Lớp P bao gồm những bài toán có thể giải được trong thời gian đa thức, tức là những bài toán này có thể được giải quyết kịp thời O(nk) trong trường hợp xấu nhất, ở đâu k là hằng số.
Những vấn đề này được gọi là tractable, trong khi những người khác được gọi là intractable or superpolynomial.
Về mặt hình thức, một thuật toán là thuật toán thời gian đa thức, nếu tồn tại một đa thức p(n) sao cho thuật toán có thể giải quyết bất kỳ trường hợp nào có kích thước n trong một thời gian O(p(n)).
Vấn đề yêu cầu Ω(n50) thời gian để giải quyết về cơ bản là khó khăn đối với n. Thuật toán thời gian đa thức được biết đến nhiều nhất chạy trong thời gianO(nk) cho giá trị khá thấp của k.
Ưu điểm của việc xem xét lớp các thuật toán đa thức thời gian là tất cả đều hợp lý deterministic single processor model of computation có thể được mô phỏng trên nhau với nhiều nhất là đa thức slow-d
NP-Class
Lớp NP bao gồm những vấn đề có thể kiểm tra được trong thời gian đa thức. NP là loại các vấn đề quyết định mà bạn có thể dễ dàng kiểm tra tính đúng đắn của một câu trả lời đã xác nhận, với sự trợ giúp của một ít thông tin bổ sung. Do đó, chúng tôi không yêu cầu một cách để tìm ra giải pháp, mà chỉ để xác minh rằng một giải pháp bị cáo buộc thực sự là đúng.
Mọi vấn đề trong lớp này có thể được giải quyết trong thời gian theo cấp số nhân bằng cách sử dụng tìm kiếm toàn diện.
P so với NP
Mọi vấn đề quyết định có thể giải được bằng thuật toán thời gian đa thức xác định cũng có thể giải được bằng thuật toán thời gian không xác định đa thức.
Tất cả các vấn đề trong P có thể được giải quyết bằng các thuật toán thời gian đa thức, trong khi tất cả các vấn đề trong NP-P là không thể chữa được.
Không biết liệu P = NP. Tuy nhiên, nhiều vấn đề đã biết trong NP với tính chất là nếu chúng thuộc P thì có thể chứng minh rằng P = NP.
Nếu P ≠ NP, có những vấn đề trong NP mà không phải trong P cũng không phải trong NP-Complete.
Vấn đề thuộc về lớp Pnếu dễ dàng tìm ra giải pháp cho vấn đề. Vấn đề thuộc vềNP, nếu dễ dàng kiểm tra một giải pháp có thể rất tẻ nhạt để tìm ra.
Stephen Cook đã trình bày bốn định lý trong bài báo của ông “Sự phức tạp của các thủ tục chứng minh định lý”. Các định lý này được nêu dưới đây. Chúng tôi hiểu rằng nhiều thuật ngữ chưa biết đang được sử dụng trong chương này, nhưng chúng tôi không có bất kỳ phạm vi nào để thảo luận mọi thứ một cách chi tiết.
Sau đây là bốn định lý của Stephen Cook:
Định lý-1
Nếu một bộ S chuỗi được chấp nhận bởi một số máy Turing không xác định trong thời gian đa thức, sau đó S có thể giảm P thành {DNF tautologies}.
Định lý-2
Các tập hợp sau đây có thể rút gọn P thành từng cặp (và do đó mỗi tập có cùng mức độ khó đa thức): {tautologies}, {DNF tautologies}, D3, {cặp biểu đồ con}.
Định lý-3
Bất cứ gì TQ(k) thuộc loại Q, $\mathbf{\frac{T_{Q}(k)}{\frac{\sqrt{k}}{(log\:k)^2}}}$ không bị ràng buộc
Đây là một TQ(k) thuộc loại Q như vậy mà $T_{Q}(k)\leqslant 2^{k(log\:k)^2}$
Định lý-4
Nếu tập hợp các chuỗi S được chấp nhận bởi một máy không xác định trong thời gian T(n) = 2n, và nếu TQ(k) là một hàm trung thực (tức là có thể đếm được trong thời gian thực) của loại Q, sau đó có một hằng số K, vì thế S có thể được công nhận bởi một máy xác định trong thời gian TQ(K8n).
Đầu tiên, ông nhấn mạnh tầm quan trọng của tính rút gọn thời gian đa thức. Có nghĩa là nếu chúng ta giảm thời gian đa thức từ bài toán này sang bài toán khác, điều này đảm bảo rằng bất kỳ thuật toán thời gian đa thức nào từ bài toán thứ hai đều có thể được chuyển đổi thành thuật toán thời gian đa thức tương ứng cho bài toán đầu tiên.
Thứ hai, ông tập trung chú ý vào NP lớp của các bài toán quyết định có thể được giải quyết trong thời gian đa thức bằng một máy tính không xác định. Hầu hết các vấn đề khó chữa thuộc về lớp này, NP.
Thứ ba, ông đã chứng minh rằng một bài toán cụ thể trong NP có tính chất là mọi bài toán khác trong NP đều có thể được rút gọn thành đa thức. Nếu bài toán thỏa mãn có thể được giải bằng thuật toán thời gian đa thức, thì mọi bài toán trong NP cũng có thể được giải theo thời gian đa thức. Nếu bất kỳ vấn đề nào trong NP là khó giải quyết, thì vấn đề thỏa mãn phải là khó chữa. Vì vậy, vấn đề thỏa mãn là vấn đề khó nhất ở NP.
Thứ tư, Cook gợi ý rằng các vấn đề khác trong NP có thể đồng nghĩa với vấn đề thỏa mãn tính chất khó khăn nhất của NP này.
Một vấn đề là ở NPC của lớp nếu nó ở NP và là hardnhư bất kỳ vấn đề nào trong NP. Một vấn đề làNP-hard nếu tất cả các bài toán trong NP là đa thức có thể giảm thời gian đối với nó, mặc dù bản thân nó có thể không nằm trong NP.
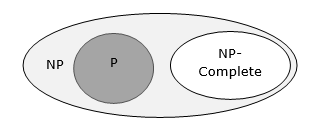
Nếu thuật toán thời gian đa thức tồn tại cho bất kỳ bài toán nào trong số này, tất cả các bài toán trong NP sẽ có thể giải được theo thời gian đa thức. Những vấn đề này được gọi làNP-complete. Hiện tượng NP-đầy đủ là quan trọng vì lý do cả lý thuyết và thực tiễn.
Định nghĩa NP-Completeness
Một ngôn ngữ B Là NP-complete nếu nó thỏa mãn hai điều kiện
B đang ở NP
Mỗi A trong NP là thời gian đa thức có thể giảm xuống B.
Nếu một ngôn ngữ đáp ứng thuộc tính thứ hai, nhưng không nhất thiết là thuộc tính đầu tiên, thì ngôn ngữ B được gọi là NP-Hard. Không chính thức, một vấn đề tìm kiếmB Là NP-Hard nếu có một số NP-Complete vấn đề A mà Turing giảm xuống B.
Vấn đề trong NP-Hard không thể được giải quyết trong thời gian đa thức, cho đến khi P = NP. Nếu một vấn đề được chứng minh là NPC, không cần phải lãng phí thời gian để cố gắng tìm ra một thuật toán hiệu quả cho nó. Thay vào đó, chúng ta có thể tập trung vào thuật toán xấp xỉ thiết kế.
Vấn đề NP-Complete
Sau đây là một số bài toán NP-Complete mà không có thuật toán thời gian đa thức nào được biết đến.
- Xác định xem một đồ thị có chu trình Hamilton hay không
- Xác định xem công thức Boolean có thỏa mãn hay không, v.v.
Vấn đề NP-Khó
Các vấn đề sau đây là NP-Hard
- Vấn đề thỏa mãn mạch
- Đặt bìa
- Bìa đỉnh
- Vấn đề nhân viên bán hàng đi du lịch
Trong bối cảnh này, bây giờ chúng ta sẽ thảo luận về TSP là NP-Complete
TSP là NP-Complete
Bài toán nhân viên bán hàng lưu động bao gồm một nhân viên bán hàng và một tập hợp các thành phố. Người bán hàng phải đến thăm từng thành phố bắt đầu từ một thành phố nhất định và quay trở lại cùng một thành phố. Thách thức của bài toán là người bán hàng du lịch muốn giảm thiểu tổng chiều dài của chuyến đi
Bằng chứng
Để chứng minh TSP is NP-Complete, trước tiên chúng ta phải chứng minh rằng TSP belongs to NP. Trong TSP, chúng tôi tìm một chuyến tham quan và kiểm tra xem chuyến tham quan có chứa mỗi đỉnh một lần hay không. Sau đó, tổng chi phí của các cạnh của chuyến tham quan được tính toán. Cuối cùng, chúng tôi kiểm tra xem chi phí là tối thiểu. Điều này có thể được hoàn thành trong thời gian đa thức. Như vậyTSP belongs to NP.
Thứ hai, chúng tôi phải chứng minh rằng TSP is NP-hard. Để chứng minh điều này, một cách là chỉ ra rằngHamiltonian cycle ≤p TSP (như chúng ta biết rằng bài toán chu trình Hamilton là không đầy đủ).
Giả định G = (V, E) là một thể hiện của chu trình Hamilton.
Do đó, một phiên bản của TSP được xây dựng. Chúng tôi tạo ra biểu đồ hoàn chỉnhG' = (V, E'), Ở đâu
$$E^{'}=\lbrace(i, j)\colon i, j \in V \:\:and\:i\neq j$$
Do đó, hàm chi phí được xác định như sau:
$$t(i,j)=\begin{cases}0 & if\: (i, j)\: \in E\\1 & otherwise\end{cases}$$
Bây giờ, giả sử rằng một chu trình Hamilton h tồn tại trong G. Rõ ràng là chi phí của mỗi cạnh trongh Là 0 trong G' vì mỗi cạnh thuộc về E. Vì thế,h có chi phí 0 trong G'. Do đó, nếu đồ thịG có chu trình Hamilton, sau đó vẽ đồ thị G' có một chuyến tham quan 0 Giá cả.
Ngược lại, chúng tôi giả định rằng G' có một chuyến du lịch h' chi phí tối đa 0. Chi phí của các cạnh trongE' Chúng tôi 0 và 1theo định nghĩa. Do đó, mỗi cạnh phải có chi phí0 như chi phí của h' Là 0. Do đó chúng tôi kết luận rằngh' chỉ chứa các cạnh trong E.
Do đó, chúng tôi đã chứng minh rằng G có chu trình Hamilton, nếu và chỉ khi G' có một chuyến tham quan với chi phí tối đa 0. TSP là NP-hoàn chỉnh.
Các thuật toán được thảo luận trong các chương trước chạy một cách có hệ thống. Để đạt được mục tiêu, một hoặc nhiều con đường đã khám phá trước đó hướng tới giải pháp cần được lưu trữ để tìm ra giải pháp tối ưu.
Đối với nhiều vấn đề, con đường dẫn đến mục tiêu là không liên quan. Ví dụ, trong bài toán N-Queens, chúng ta không cần quan tâm đến cấu hình cuối cùng của các nữ hoàng cũng như thứ tự các nữ hoàng được thêm vào.
Leo đồi
Hill Climbing là một kỹ thuật để giải quyết các vấn đề tối ưu hóa nhất định. Trong kỹ thuật này, chúng tôi bắt đầu với một giải pháp phụ tối ưu và giải pháp được cải thiện lặp đi lặp lại cho đến khi một số điều kiện được tối đa hóa.
Ý tưởng bắt đầu với một giải pháp phụ tối ưu được so sánh với việc bắt đầu từ chân đồi, việc cải thiện giải pháp được so sánh với việc đi bộ lên đồi, và cuối cùng tối đa hóa một số điều kiện so với việc lên đến đỉnh đồi.
Do đó, kỹ thuật leo đồi có thể được coi là các giai đoạn sau:
- Xây dựng một giải pháp tối ưu phụ tuân theo các ràng buộc của bài toán
- Cải thiện giải pháp từng bước
- Cải thiện giải pháp cho đến khi không thể cải thiện được nữa
Kỹ thuật Hill Climbing chủ yếu được sử dụng để giải các bài toán khó về mặt tính toán. Nó chỉ nhìn vào trạng thái hiện tại và trạng thái tương lai trước mắt. Do đó, kỹ thuật này hiệu quả về bộ nhớ vì nó không duy trì cây tìm kiếm.
Algorithm: Hill Climbing
Evaluate the initial state.
Loop until a solution is found or there are no new operators left to be applied:
- Select and apply a new operator
- Evaluate the new state:
goal -→ quit
better than current state -→ new current stateCải tiến lặp đi lặp lại
Trong phương pháp cải tiến lặp đi lặp lại, giải pháp tối ưu đạt được bằng cách tiến tới giải pháp tối ưu trong mỗi lần lặp lại. Tuy nhiên, kỹ thuật này có thể gặp cực đại cục bộ. Trong tình huống này, không có trạng thái nào gần đó để có giải pháp tốt hơn.
Vấn đề này có thể được tránh bằng các phương pháp khác nhau. Một trong những phương pháp này là ủ mô phỏng.
Khởi động lại ngẫu nhiên
Đây là một phương pháp khác để giải quyết vấn đề của optima cục bộ. Kỹ thuật này thực hiện một loạt các tìm kiếm. Mỗi lần, nó bắt đầu từ trạng thái ban đầu được tạo ngẫu nhiên. Do đó, có thể thu được optima hoặc giải pháp gần như tối ưu so với các giải pháp của các tìm kiếm được thực hiện.
Các vấn đề của kỹ thuật leo đồi
Maxima địa phương
Nếu heuristic không lồi, Hill Climbing có thể hội tụ thành cực đại cục bộ, thay vì cực đại toàn cục.
Ridges and Alleys
Nếu hàm mục tiêu tạo ra một sườn núi hẹp, thì người leo núi chỉ có thể lên đỉnh hoặc xuống hẻm bằng cách chạy zic zắc. Trong trường hợp này, người leo núi cần thực hiện những bước rất nhỏ, đòi hỏi nhiều thời gian hơn để đạt được mục tiêu.
Cao nguyên
Gặp phải sự cố định khi không gian tìm kiếm bằng phẳng hoặc đủ phẳng mà giá trị được trả về bởi hàm mục tiêu không thể phân biệt được với giá trị được trả về cho các vùng lân cận, do độ chính xác được máy sử dụng để biểu thị giá trị của nó.
Độ phức tạp của kỹ thuật leo đồi
Kỹ thuật này không bị các vấn đề liên quan đến không gian, vì nó chỉ xem xét trạng thái hiện tại. Các đường dẫn đã khám phá trước đây không được lưu trữ.
Đối với hầu hết các vấn đề trong kỹ thuật Leo đồi khởi động lại ngẫu nhiên, một giải pháp tối ưu có thể đạt được trong thời gian đa thức. Tuy nhiên, đối với các bài toán NP-Complete, thời gian tính toán có thể là cấp số nhân dựa trên số lượng cực đại cục bộ.
Các ứng dụng của kỹ thuật leo đồi
Kỹ thuật Hill Climbing có thể được sử dụng để giải quyết nhiều vấn đề, trong đó trạng thái hiện tại cho phép một chức năng đánh giá chính xác, chẳng hạn như Network-Flow, Traveling Salesman problem, 8-Queens, Integrated Circuit design, v.v.
Hill Climbing cũng được sử dụng trong phương pháp học tập quy nạp. Kỹ thuật này được sử dụng trong robot để phối hợp giữa nhiều robot trong một đội. Có nhiều vấn đề khác khi kỹ thuật này được sử dụng.
Thí dụ
Kỹ thuật này có thể được áp dụng để giải quyết vấn đề nhân viên bán hàng đi du lịch. Đầu tiên, một giải pháp ban đầu được xác định là đi thăm tất cả các thành phố chính xác một lần. Do đó, giải pháp ban đầu này không phải là tối ưu trong hầu hết các trường hợp. Thậm chí giải pháp này có thể rất kém. Thuật toán Hill Climbing bắt đầu với một giải pháp ban đầu như vậy và thực hiện các cải tiến cho nó theo cách lặp đi lặp lại. Cuối cùng, một lộ trình ngắn hơn nhiều có thể đạt được.