DAA - Biểu đồ nhiều tầng
Biểu đồ nhiều tầng G = (V, E) là một đồ thị có hướng trong đó các đỉnh được phân chia thành k (Ở đâu k > 1) số lượng tập con rời rạc S = {s1,s2,…,sk}sao cho cạnh (u, v) nằm trong E, thì u Є s i và v Є s 1 + 1 cho một số tập con trong phân hoạch và |s1| = |sk| = 1.
Đỉnh s Є s1 nó được gọi là source và đỉnh t Є sk được gọi là sink.
Gthường được giả định là một đồ thị có trọng số. Trong đồ thị này, chi phí của một cạnh (i, j) được biểu thị bằng c (i, j) . Do đó, chi phí của đường dẫn từ nguồns để chìm t là tổng chi phí của mỗi cạnh trong đường dẫn này.
Bài toán biểu đồ nhiều tầng là tìm đường dẫn với chi phí tối thiểu từ nguồn s để chìm t.
Thí dụ
Hãy xem xét ví dụ sau để hiểu khái niệm về đồ thị nhiều tầng.
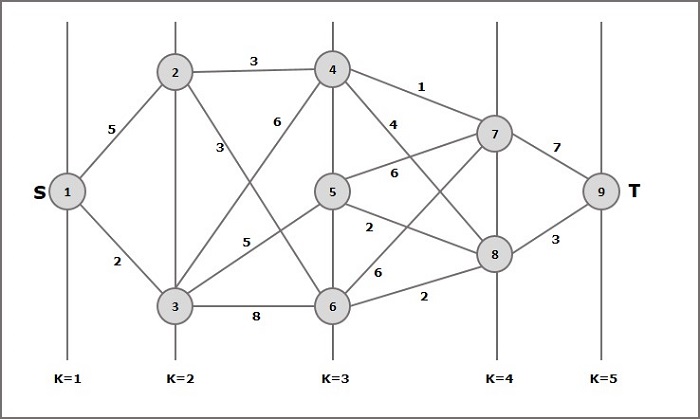
Theo công thức, chúng ta phải tính chi phí (i, j) sử dụng các bước sau
Bước-1: Chi phí (K-2, j)
Trong bước này, ba nút (nút 4, 5, 6) được chọn là j. Do đó, chúng tôi có ba tùy chọn để chọn chi phí tối thiểu ở bước này.
Chi phí (3, 4) = tối thiểu {c (4, 7) + Chi phí (7, 9), c (4, 8) + Chi phí (8, 9)} = 7
Chi phí (3, 5) = tối thiểu {c (5, 7) + Chi phí (7, 9), c (5, 8) + Chi phí (8, 9)} = 5
Chi phí (3, 6) = tối thiểu {c (6, 7) + Chi phí (7, 9), c (6, 8) + Chi phí (8, 9)} = 5
Bước 2: Chi phí (K-3, j)
Hai nút được chọn là j vì ở giai đoạn k - 3 = 2 có hai nút là 2 và 3. Vì vậy, giá trị i = 2 và j = 2 và 3.
Chi phí (2, 2) = min {c (2, 4) + Cost (4, 8) + Cost (8, 9), c (2, 6) +
Chi phí (6, 8) + Chi phí (8, 9)} = 8
Chi phí (2, 3) = {c (3, 4) + Chi phí (4, 8) + Chi phí (8, 9), c (3, 5) + Chi phí (5, 8) + Chi phí (8, 9), c (3, 6) + Chi phí (6, 8) + Chi phí (8, 9)} = 10
Bước-3: Chi phí (K-4, j)
Chi phí (1, 1) = {c (1, 2) + Chi phí (2, 6) + Chi phí (6, 8) + Chi phí (8, 9), c (1, 3) + Chi phí (3, 5) + Chi phí (5, 8) + Chi phí (8, 9))} = 12
c (1, 3) + Chi phí (3, 6) + Chi phí (6, 8 + Chi phí (8, 9))} = 13
Do đó, con đường có chi phí tối thiểu là 1→ 3→ 5→ 8→ 9.