Lớp NP Khó và NP-Hoàn thành
Một vấn đề là ở NPC của lớp nếu nó ở NP và là hardnhư bất kỳ vấn đề nào trong NP. Một vấn đề làNP-hard nếu tất cả các bài toán trong NP là đa thức có thể giảm thời gian đối với nó, mặc dù bản thân nó có thể không có trong NP.
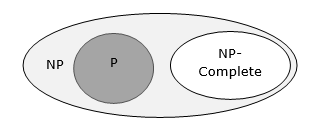
Nếu tồn tại thuật toán thời gian đa thức cho bất kỳ bài toán nào trong số này, thì tất cả các bài toán trong NP sẽ có thể giải được theo thời gian đa thức. Những vấn đề này được gọi làNP-complete. Hiện tượng NP-đầy đủ là quan trọng vì lý do cả lý thuyết và thực tiễn.
Định nghĩa NP-Completeness
Một ngôn ngữ B Là NP-complete nếu nó thỏa mãn hai điều kiện
B đang ở NP
Mỗi A trong NP là thời gian đa thức có thể giảm xuống B.
Nếu một ngôn ngữ đáp ứng thuộc tính thứ hai, nhưng không nhất thiết là thuộc tính đầu tiên, thì ngôn ngữ B được gọi là NP-Hard. Không chính thức, một vấn đề tìm kiếmB Là NP-Hard nếu có một số NP-Complete vấn đề A mà Turing giảm xuống B.
Vấn đề trong NP-Hard không thể được giải quyết trong thời gian đa thức, cho đến khi P = NP. Nếu một vấn đề được chứng minh là NPC, không cần phải lãng phí thời gian để cố gắng tìm ra một thuật toán hiệu quả cho nó. Thay vào đó, chúng ta có thể tập trung vào thuật toán xấp xỉ thiết kế.
Vấn đề NP-Complete
Sau đây là một số bài toán NP-Complete mà không có thuật toán thời gian đa thức nào được biết đến.
- Xác định xem một đồ thị có chu trình Hamilton hay không
- Xác định xem công thức Boolean có thỏa mãn hay không, v.v.
Vấn đề NP-Khó
Các vấn đề sau đây là NP-Hard
- Vấn đề thỏa mãn mạch
- Đặt bìa
- Bìa đỉnh
- Vấn đề nhân viên bán hàng đi du lịch
Trong bối cảnh này, bây giờ chúng ta sẽ thảo luận về TSP là NP-Complete
TSP là NP-Complete
Bài toán nhân viên bán hàng lưu động bao gồm một nhân viên bán hàng và một tập hợp các thành phố. Người bán hàng phải đến thăm từng thành phố bắt đầu từ một thành phố nhất định và trở về cùng một thành phố. Thách thức của bài toán là người bán hàng du lịch muốn giảm thiểu tổng chiều dài của chuyến đi
Bằng chứng
Để chứng minh TSP is NP-Complete, trước tiên chúng ta phải chứng minh rằng TSP belongs to NP. Trong TSP, chúng tôi tìm một chuyến tham quan và kiểm tra xem chuyến tham quan có chứa mỗi đỉnh một lần hay không. Sau đó, tổng chi phí của các cạnh của chuyến tham quan được tính toán. Cuối cùng, chúng tôi kiểm tra xem chi phí là tối thiểu. Điều này có thể được hoàn thành trong thời gian đa thức. Như vậyTSP belongs to NP.
Thứ hai, chúng tôi phải chứng minh rằng TSP is NP-hard. Để chứng minh điều này, một cách là chỉ ra rằngHamiltonian cycle ≤p TSP (như chúng ta biết rằng bài toán chu trình Hamilton là không đầy đủ).
Giả định G = (V, E) là một thể hiện của chu trình Hamilton.
Do đó, một phiên bản của TSP được xây dựng. Chúng tôi tạo ra biểu đồ hoàn chỉnhG' = (V, E'), Ở đâu
$$ E ^ {'} = \ lbrace (i, j) \ dấu hai chấm i, j \ trong V \: \: và \: i \ neq j $$
Do đó, hàm chi phí được xác định như sau:
$$ t (i, j) = \ begin {case} 0 & if \: (i, j) \: \ in E \\ 1 & nếu không thì \ end {case} $$
Bây giờ, giả sử rằng một chu trình Hamilton h tồn tại trong G. Rõ ràng là chi phí của mỗi cạnh trongh Là 0 trong G' vì mỗi cạnh thuộc về E. Vì thế,h có chi phí 0 trong G'. Do đó, nếu đồ thịG có chu trình Hamilton thì đồ thị G' có một chuyến tham quan 0 Giá cả.
Ngược lại, chúng tôi giả định rằng G' có một chuyến du lịch h' chi phí tối đa 0. Chi phí của các cạnh trongE' Chúng tôi 0 và 1theo định nghĩa. Do đó, mỗi cạnh phải có chi phí0 như chi phí của h' Là 0. Do đó chúng tôi kết luận rằngh' chỉ chứa các cạnh trong E.
Do đó, chúng tôi đã chứng minh rằng G có chu trình Hamilton, nếu và chỉ khi G' có một chuyến tham quan với chi phí tối đa 0. TSP là NP-hoàn chỉnh.