DAA - Mẫu hợp nhất tối ưu
Hợp nhất một tập hợp các tệp được sắp xếp có độ dài khác nhau thành một tệp được sắp xếp. Chúng tôi cần tìm một giải pháp tối ưu, nơi tệp kết quả sẽ được tạo trong thời gian tối thiểu.
Nếu số lượng tệp được sắp xếp được cung cấp, có nhiều cách để hợp nhất chúng thành một tệp được sắp xếp duy nhất. Sự hợp nhất này có thể được thực hiện theo cặp khôn ngoan. Do đó, kiểu hợp nhất này được gọi là2-way merge patterns.
Vì, các quá trình ghép nối khác nhau yêu cầu lượng thời gian khác nhau, trong chiến lược này, chúng tôi muốn xác định một cách tối ưu để hợp nhất nhiều tệp với nhau. Ở mỗi bước, hai chuỗi ngắn nhất được hợp nhất.
Để hợp nhất một p-record file và một q-record file yêu cầu có thể p + q kỷ lục di chuyển, lựa chọn hiển nhiên là hợp nhất hai tệp nhỏ nhất với nhau ở mỗi bước.
Các mẫu hợp nhất hai chiều có thể được biểu diễn bằng cây hợp nhất nhị phân. Hãy để chúng tôi xem xét một tập hợpn các tệp được sắp xếp {f1, f2, f3, …, fn}. Ban đầu, mỗi phần tử này được coi là một cây nhị phân nút đơn. Để tìm giải pháp tối ưu này, thuật toán sau được sử dụng.
Algorithm: TREE (n)
for i := 1 to n – 1 do
declare new node
node.leftchild := least (list)
node.rightchild := least (list)
node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight)
insert (list, node);
return least (list);Khi kết thúc thuật toán này, trọng số của nút gốc đại diện cho chi phí tối ưu.
Thí dụ
Ta xét các tập đã cho, f 1 , f 2 , f 3 , f 4 và f 5 có số phần tử lần lượt là 20, 30, 10, 5 và 30.
Nếu các hoạt động hợp nhất được thực hiện theo trình tự được cung cấp, thì
M1 = merge f1 and f2 => 20 + 30 = 50
M2 = merge M1 and f3 => 50 + 10 = 60
M3 = merge M2 and f4 => 60 + 5 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Do đó, tổng số hoạt động là
50 + 60 + 65 + 95 = 270
Bây giờ, câu hỏi đặt ra là có giải pháp nào tốt hơn không?
Sắp xếp các số theo kích thước của chúng theo thứ tự tăng dần, chúng ta nhận được chuỗi sau:
f4, f3, f1, f2, f5
Do đó, các hoạt động hợp nhất có thể được thực hiện trên trình tự này
M1 = merge f4 and f3 => 5 + 10 = 15
M2 = merge M1 and f1 => 15 + 20 = 35
M3 = merge M2 and f2 => 35 + 30 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Do đó, tổng số hoạt động là
15 + 35 + 65 + 95 = 210
Rõ ràng, cái này tốt hơn cái trước.
Trong bối cảnh này, bây giờ chúng ta sẽ giải quyết vấn đề bằng cách sử dụng thuật toán này.
Bộ ban đầu

Bước 1
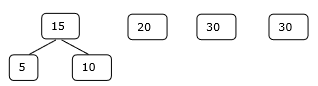
Bước 2
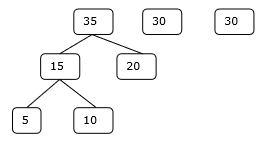
Bước 3
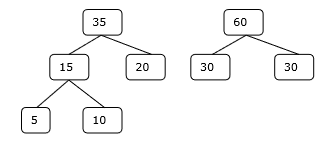
Bước 4
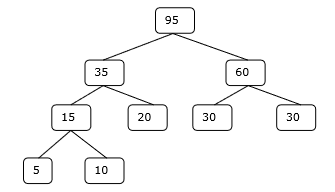
Do đó, giải pháp có 15 + 35 + 60 + 95 = 205 số so sánh.