DAA - Đường dẫn ngắn nhất
Thuật toán Dijkstra
Thuật toán Dijkstra giải bài toán đường đi ngắn nhất nguồn đơn trên đồ thị có trọng số có hướng G = (V, E) , trong đó tất cả các cạnh đều không âm (tức là w (u, v) ≥ 0 đối với mỗi cạnh (u, v ) Є E ).
Trong thuật toán sau, chúng ta sẽ sử dụng một hàm Extract-Min(), trích xuất nút có khóa nhỏ nhất.
Algorithm: Dijkstra’s-Algorithm (G, w, s)
for each vertex v Є G.V
v.d := ∞
v.∏ := NIL
s.d := 0
S := Ф
Q := G.V
while Q ≠ Ф
u := Extract-Min (Q)
S := S U {u}
for each vertex v Є G.adj[u]
if v.d > u.d + w(u, v)
v.d := u.d + w(u, v)
v.∏ := uPhân tích
Độ phức tạp của thuật toán này hoàn toàn phụ thuộc vào việc thực hiện hàm Extract-Min. Nếu hàm min trích xuất được thực hiện bằng cách sử dụng tìm kiếm tuyến tính, thì độ phức tạp của thuật toán này làO(V2 + E).
Trong thuật toán này, nếu chúng ta sử dụng min-heap trên đó Extract-Min() hàm hoạt động để trả về nút từ Q với khóa nhỏ nhất, độ phức tạp của thuật toán này có thể được giảm thêm.
Thí dụ
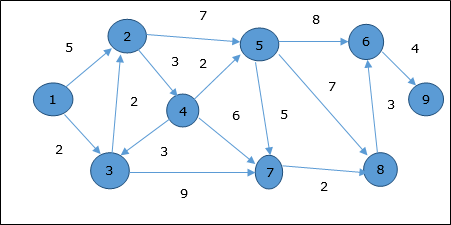
Hãy để chúng tôi xem xét đỉnh 1 và 9là đỉnh xuất phát và đích tương ứng. Ban đầu, tất cả các đỉnh ngoại trừ đỉnh bắt đầu được đánh dấu bằng ∞ và đỉnh bắt đầu được đánh dấu bằng0.
| Đỉnh | Ban đầu | Bước 1 V 1 | Bước 2 V 3 | Bước 3 V 2 | Bước 4 V 4 | Bước 5 V 5 | Bước 6 V 7 | Bước 7 V 8 | Bước 8 V 6 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | ∞ | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 3 | ∞ | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 4 | ∞ | ∞ | ∞ | 7 | 7 | 7 | 7 | 7 | 7 |
| 5 | ∞ | ∞ | ∞ | 11 | 9 | 9 | 9 | 9 | 9 |
| 6 | ∞ | ∞ | ∞ | ∞ | ∞ | 17 | 17 | 16 | 16 |
| 7 | ∞ | ∞ | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| số 8 | ∞ | ∞ | ∞ | ∞ | ∞ | 16 | 13 | 13 | 13 |
| 9 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 20 |
Do đó, khoảng cách tối thiểu của đỉnh 9 từ đỉnh 1 Là 20. Và con đường là
1 → 3 → 7 → 8 → 6 → 9
Đường dẫn này được xác định dựa trên thông tin tiền nhiệm.
Thuật toán Bellman Ford
Thuật toán này giải quyết vấn đề đường đi ngắn nhất nguồn duy nhất của đồ thị có hướng G = (V, E)trong đó trọng số các cạnh có thể âm. Hơn nữa, thuật toán này có thể được áp dụng để tìm đường đi ngắn nhất, nếu không tồn tại bất kỳ chu trình có trọng số âm nào.
Algorithm: Bellman-Ford-Algorithm (G, w, s)
for each vertex v Є G.V
v.d := ∞
v.∏ := NIL
s.d := 0
for i = 1 to |G.V| - 1
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
v.d := u.d +w(u, v)
v.∏ := u
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
return FALSE
return TRUEPhân tích
Đầu tiên for vòng lặp được sử dụng để khởi tạo, chạy trong O(V)lần. Tiếp theofor vòng lặp chạy |V - 1| vượt qua các cạnh, mấtO(E) lần.
Do đó, thuật toán Bellman-Ford chạy trong O(V, E) thời gian.
Thí dụ
Ví dụ sau đây cho thấy cách thức hoạt động của thuật toán Bellman-Ford từng bước. Đồ thị này có một cạnh âm nhưng không có bất kỳ chu kỳ âm nào, do đó vấn đề có thể được giải quyết bằng cách sử dụng kỹ thuật này.
Tại thời điểm khởi tạo, tất cả các đỉnh ngoại trừ nguồn được đánh dấu bằng ∞ và nguồn được đánh dấu bằng 0.
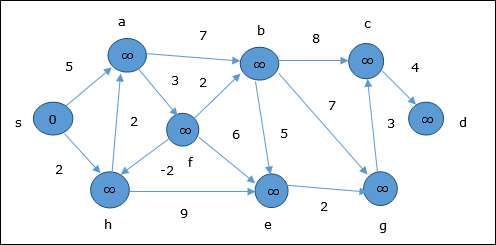
Trong bước đầu tiên, tất cả các đỉnh có thể truy cập từ nguồn được cập nhật bằng chi phí tối thiểu. Do đó, các đỉnha và h được cập nhật.
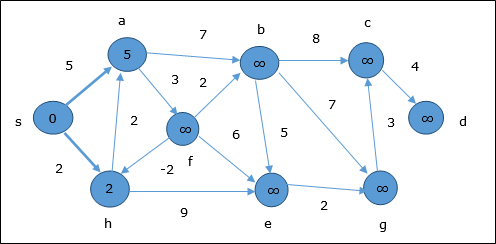
Trong bước tiếp theo, các đỉnh a, b, f và e được cập nhật.
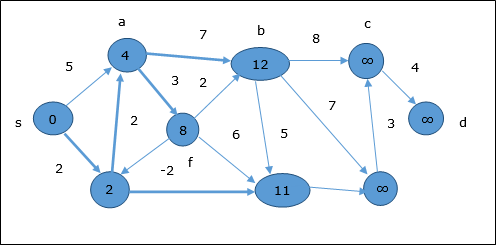
Theo cùng một logic, trong bước này các đỉnh b, f, c và g được cập nhật.
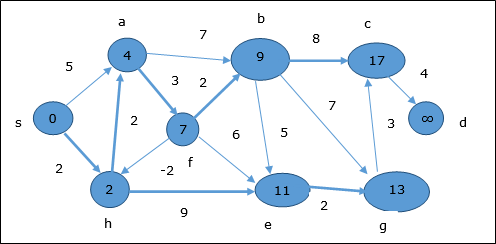
Đây, các đỉnh c và d được cập nhật.
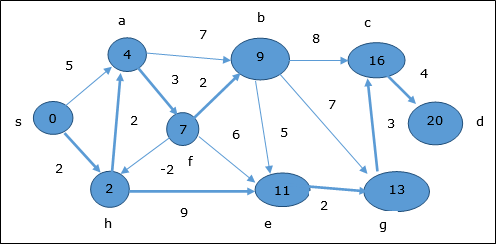
Do đó, khoảng cách tối thiểu giữa các đỉnh s và đỉnh d Là 20.
Dựa trên thông tin tiền nhiệm, con đường là s → h → e → g → c → d